astronomia fundamental e as

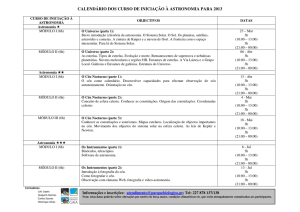
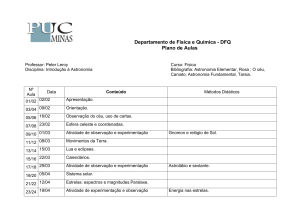
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
1 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Marcelo Assafin
OV/UFRJ
Apresentação......................................................................................................................3
1. Introdução........................................................................................................................4
2. Posições de Objetos Astronômicos.................................................................................5
2.1. Sistema de Coordenadas Equatorial Celeste e Altazimutal.....................................7
2.1.1 A Esfera Celeste ....................................................................................................7
2.1.2 Sistema de Coordenadas Altazimutais.................................................................10
2.1.3 Sistema de Coordenadas Equatoriais Celestes....................................................11
2.2 Variação de Coordenadas Devido a Rotação da Terra ...........................................13
2.2.1 Marés .....................................................................................................................15
2.3 Variação de Coordenadas Devido a Precessão e Nutação .....................................16
2.4 Variação de Coordenadas Devido ao Movimento do Polo ......................................18
2.5 Variação de Coordenadas Devido ao Movimento Orbital da Terra...........................19
2.5.1 Paralaxe Anual.......................................................................................................20
2.5.2 Aberração Anual.....................................................................................................21
2.6 Movimento do Sol na Galáxia....................................................................................22
2.6.1 Sistema de Coordenadas Galácticas......................................................................23
2.7 Relação entre Sistemas de Coordenadas .................................................................24
3. Tempo..............................................................................................................................27
3.1 Tempo Solar ..............................................................................................................28
3.1.1 Fusos Horários .......................................................................................................29
3.2 Tempo Sideral ...........................................................................................................31
3.3 Tempo das Efemérides e Tempo Dinâmico................................................................32
3.4 Tempo Atômico...........................................................................................................32
3.5 Tempo Universal Coordenado....................................................................................33
3.6 Calendários.................................................................................................................34
4. Catálogos Astrométricos ..................................................................................................35
4.1 Catálogos de Posição - Histórico................................................................................35
4.2 Catálogos de Posição Modernos................................................................................39
4.3 Os Novos Catálogos Astrométricos na Era HIPPARCOS..........................................41
4.4 Catálogos Astrométricos: como se apresentam e como acessá-los?........................44
4.5 Catálogos das Futuras Missões Espaciais: Astrometria Aplicada a Astrofísica.........45
4.5.1 A Missão SIM...........................................................................................................45
4.5.1.1 Populações Galácticas.........................................................................................47
4.5.1.2 Estrutura da Galáxia.............................................................................................48
4.5.1.3 Astronomia Extragaláxia.......................................................................................48
4.5.2 A Missão GAIA.........................................................................................................49
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
2 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Rio – Março, 2004
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
3 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
APRESENTAÇÃO
Este texto abrange o conteúdo de 4 horas de aula do tema Astronomia Fundamental e
Astrometria da disciplina “Fundamentos da Astronomia”, oferecida na Física.
São apresentados o cenário passado e atual da área, e as idéias básicas, acessíveis
para estudantes do segundo grau e do primeiro ano de cursos universitários nas áreas de
física, matemática, astronomia ou cursos correlatos.
O objetivo é apresentar os conceitos básicos de posição dos astros, sistemas de
referência de espaço e de tempo, mostrar a importância dos catálogos de posição, da
determinação de distâncias, a relação da Astronomia Fundamental e da Astrometria com as
demais ciências astrofísicas, a descrição de fenômenos astronômicos e terrestres relacionados
aos movimentos da Terra no espaço, aplicações da Astronomia Fundamental à vida civil
(principalmente o tempo). Para tanto, reforçamos alguns conceitos básicos de astronomia já
introduzidos, e introduzimos sucintamente novos.
O texto está estruturado de forma que as idéias centrais estão no texto principal, que é
subdivido em seções, algumas delas com subseções. No meio do texto, alguns exercícios são
apresentados, quando necessário, as vezes com sugestões e roteiros para serem
solucionados. Eles devem ser examinados, analisados cuidadosamente e resolvidos pelos
estudantes interessados em bem assimilar o conteúdo do curso. A dificuldade destes
exercícios é variável e muitos deles apresentam resultados interessantes. Não são dadas
respostas, os alunos devem trazer os exercícios resolvidos e discutí-los em sala.
Algumas das figuras foram tiradas de textos na Internet e em textos de astronomia
apresentados na forma de CD. Muitas aparecem em vários textos diferentes, o que dificulta ou
impossibilita a definição clara de sua origem. Algumas das figuras, porém, creditamos aqui a
notas de aula eletrônicas gentilmente cedidas pelos Profs. Roberto Boczko e Prof. Gastão B.
Lima Neto do IAG/USP, e Prof. Alexandre H. Andrei do ON/MCT-OV/UFRJ-GEA. Para
simplificação, os créditos de todas as figuras foram omitidos.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
4 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
1. INTRODUÇÃO
Fig. 1.1 – Observatório do Valongo/UFRJ.
Na figura 1.1 vemos o campus do Observatório do Valongo (OV), da UFRJ. Ele está
localizado no alto de um morro, bem próximo ao centro financeiro da cidade do Rio de Janeiro.
A partir da Rua Marechal Floriano, segue-se a pé (pela calçada) ou de carro (pelo asfalto),
seguindo o sentido do trânsito, por uma rua secundária, a Rua Senador Pompeu, até chegar
ao No. 43 da Ladeira do Pedro Antônio. Veja abaixo, na fig.1.2, o mapa da região, que mostra
como chegar ao OV, para fazer Astronomia.
Fig. 1.2 – Mapa da região do entorno do Observatório do Valongo, UFRJ.
Repare no conjunto de regras, convenções e nomenclaturas usadas para designar a
localidade, o endereço do Observatório, e as vias de acesso ao mesmo, ou seja, o mapa da
região. Falamos em ruas e calçadas, falamos em sentidos, falamos em nomenclaturas
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
5 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
específicas (Rua, números, etc), representamos esses elementos com símbolos específicos, e
com regras específicas. Com a Astronomia Fundamental, dá-se o mesmo. É a Astronomia
Fundamental a ciência responsável pela cartografia do Universo, isto é, pela definição de
sistemas de referência espaciais e temporais, segundo um conjunto de convenções e normas
de valor universal. É seu papel realizar o censo de todos os corpos celestes, isto é, determinar
suas posições espaciais no tempo.
2. POSIÇÕES DE OBJETOS ASTRONÔMICOS
É essencial o conhecimento da posição, em qualquer instante de tempo, dos corpos
celestes na investigação do Cosmos. Isto é, saber em que direção no céu se encontram, qual a
sua distância até nós, de onde e para onde se movem. A medida em que o Curso avança, vai
ficando mais claro que tipo de conhecimento se busca, a partir da informação da posição
espacial dos corpos celestes em função do tempo.
Do ponto de vista do conhecimento científico atual, devemos definir de forma
matematicamente fundada, um sistema de referência de forma que, considerando o próprio
observador e o astro sendo observado, esse sistema possa descrever da forma mais simples e
coerente a posição e movimento do astro. Uma vez estabelecido o sistema de referência,
passamos a definir o sistema de coordenadas, que igualmente deve ser escolhido de forma a
tornar mais simples e adequada a descrição da posição e movimento do astro dentro do
sistema de referência escolhido. Um exemplo muito familiar é o sistema de coordenadas
cartesiano, com seus 3 eixos ortogonais x, y e z. Mas há outros: cilíndricos, esféricos, etc.
Em Astronomia, é muito comum usar o sistema de coordenadas esférico. Você já
conhece esse sistema: lembre-se das coordenadas geográficas da Terra, latitude e longitude.
Apenas os sistemas de coordenadas astronômicos mais importantes, serão apresentados
neste Curso, e mesmo assim sucintamente, pois uma abordagem mais profunda foge ao nosso
escopo. Apesar de conceitualmente diferentes, em geral costuma-se empregar indistintamente
os termos “sistema de referência” e “sistema de coordenadas”. Por motivos de simplificação,
faremos o mesmo aqui, porém ressaltando a diferença, caso seja importante.
De um ponto de vista mais conceitual, não é qualquer sistema de referência que nos
permite acessar a posição, distância e movimento de um corpo celeste, rigorosamente de
acordo com a Mecânica Newtoniana. Neste caso, o sistema de referência a ser adotado deve
ser inercial e a medida do tempo associada a medida de movimento, deve ser uniforme. Em
outras palavras, um corpo se movendo no espaço tendo sobre ele a ação de uma força
resultante nula, deve ter uma trajetória descrita como sendo igual a de uma linha reta, onde
distâncias iguais são cobertas em intervalos de tempos iguais nesse referencial. A trajetória do
corpo pode ainda ser descrita por um ponto fixo, no caso particular de velocidade nula. Sendo
assim, há dois tipos de referenciais astronômicos que precedem a própria Mecânica
Newtoniana, um espacial, outro temporal. Eles devem estar previamente disponíveis, para
que o movimento dos corpos celestes possa ser descrito e interpretado de forma coerente na
Mecânica Newtoniana. São eles o referencial inercial, ligado ao espaço propriamente dito, e
ao qual nós vínhamos nos referindo, e o referencial de tempo uniforme, mais comumente
referido em termos de escalas de tempo.
A Astronomia Fundamental, sendo o ramo que idealiza e estuda os referenciais em
Astronomia, tem como tema chave a concepção e a materialização dos referenciais inerciais
espaciais e das escalas de tempo uniforme. Na verdade, hoje em dia, apenas a tarefa da
concepção de uma escala uniforme de tempo e sua interrelação com as demais escalas é
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
6 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
efetivamente da responsabilidade da Astronomia Fundamental, posto que a materialização
mais precisa e prática é hoje feita com relógios atômicos, e faz parte do “universo” da
engenharia eletrônica. Falaremos mais sobre escalas de tempo no Capítulo 3.
A materialização dos eixos de um referencial inercial depende de direções baseadas nas
posições aparentes observadas de corpos celestes, como estrelas, por exemplo. Pergunta:
pode, do ponto de vista conceitual, existir uma materialização perfeita de um referencial
inercial? (responda com suas palavras, como exercício).
Materializar um referencial inercial significa estabelecer eixos, ou ainda planos, cujas
direções no espaço sejam conhecidas no tempo, e possam ser reproduzidas. Essa
materialização traduz-se em catálogos de objetos celestes, cuja posição e movimento (entre
outras informações, como brilho, etc) são listados de acordo com um sistema de coordenadas
conveniente. Catálogos criados com o fim de representarem ou materializarem sistemas de
referência são ditos catálogos astrométricos.
A percepção dos planos fundamentais e do sistema de coordenadas mais adequado foi
mudando com o passar do tempo, e mesmo na antiguidade, quando registram-se os primeiros
catálogos estelares da história, ainda era bem remota a idéia de inercialidade e da
uniformidade do tempo, até porque a Mecânica Newtoniana ainda nem havia nascido. Na
época atual, os catálogos com posições óticas mais precisas originam-se de missões espaciais,
como a do Satélite HIPPARCOS. Há também os catálogos de posições rádio, obtidas a partir
de medidas simultâneas de quasares, com antenas rádio espalhadas em todo o globo, usando
técnicas de interferometria.
Fig. 2.1. Evolução da precisão das posições de catálogos representativos de cada época.
Na faixa ótica do espectro eletromagnético, via de regra os catálogos listam posições e
movimento de estrelas, já que esses são os objetos celestes visíveis mais comuns de nossa
Galáxia e, uma vez podendo ser acessadas de qualquer ponto da Terra, e uma vez sendo
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
7 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
relativamente abundantes, tornam-se pontos fiduciais ideais para representar um dado sistema
de referência. No Capítulo 4, damos um histórico da evolução dos catálogos, desde a
antiguidade até os dias atuais.
A medida que o tempo passa, mais estrelas, de brilho mais fraco, vão sendo incluídas
nos catálogos, com precisão cada vez melhor. Pergunta: você sabe o que é “precisão”?
(responda como exercício).
Tendo em vista levar o sistema inercial a objetos de brilho cada vez menor,
modernamente tem sido levado a cabo programas de construção de catálogos astrométricos
de virtualmente milhões de estrelas. É o caso do catálogo UCAC (do inglês “USNO CCD
Astrograph Catalog”) do United States Naval Observatory (USNO), de 40 milhões de estrelas
com precisão de 20mas a 70mas (1mas = 0”,001 ou 1 mili-segundo de arco), e do USNO-B1
de 500 milhões de estrelas com precisão de 200mas.
Quanto melhor a precisão na medida da posição e do movimento de um astro,
melhor será a qualidade da informação da cinemática desse corpo, seja qual for a estrutura no
Universo da qual ele faça parte (sistema solar, aglomerado, Galáxia, etc). A Fig. 2.1 dá uma
idéia da evolução da precisão da medida da posição dos astros ao longo da história. Em geral,
ao conjunto de técnicas envolvidas na determinação precisa da posição dos astros, dá-se o
nome de Astrometria. Em grande parte, a evolução da precisão das medidas astrométricas
vem da evolução dos instrumentos de observação utilizados, em particular a partir da
introdução dos telescópios desde Galileu (1609), e agora com o advento de missões espaciais
astrométricas como a missão HiPParCoS (High Precision Paralaxis Collecting Sattelite). A
palavra paralaxe está associada a determinação de distância, tema que veremos mais adiante
(Seção 2.5.1).
Estude a Fig. 2.1. Pergunta: qual deve ser a precisão da posição para daqui a 30
anos? (responda como exercício).
2.1 Sistema de Coordenadas Equatorial Celeste e Altazimutal
Um sistema de coordenadas esféricas muito importante em Astronomia foi concebido e
pela primeira vez apresentado por Hevelius, já em 1690. Ele consiste basicamente em
estender o nosso conhecido Sistema de Coordenadas Geográficas para o céu. É o chamado
Sistema de Coordenadas Equatoriais Celestes. Antes, porém, vamos definir alguns
elementos básicos.
2.1.1 A Esfera Celeste
No Universo, os astros se distribuem em um espaço tridimensional. Contudo, devido a
imensa distância que separa estes astros da Terra, ao observarmos o céu nos temos a
impressão que todos estes astros se encontram em uma esfera, a que denominamos Esfera
Celeste. A Esfera Celeste não tem um raio definido, assim consideramos este raio como
infinito. Como a distância entre um observador qualquer e o centro da Terra (cerca de 6400
km) é muito menor que a distância aos astros (a Lua está, em média a 380.000 km, o Sol a 150
milhões de km ou 1U.A., e as estrelas estão muito alem do sistema solar) o erro que se faz é,
na maioria dos casos, desprezível.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
8 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.2 – A Esfera Celeste.
A Fig. 2.2 ilustra a visão da Esfera Celeste, para um observador situado na superfície da
Terra. O ponto imediatamente a sua cabeça recebe o nome de Zênite. O Plano do Horizonte,
ou simplesmente Horizonte, é o plano perpendicular a linha imaginária que liga o observador
ao Zênite. Todos os elementos descritos estão envolvidos pela Esfera Celeste. É em sua
superfície que descrevemos a posição aparente dos astros no céu.
A Esfera Celeste pode estar centrada no observador, porém as vezes é mais
conveniente admitirmos que o centro esteja em algum outro ponto, no centro da Terra ou no
centro do Sol, ou mesmo ainda no baricentro do sistema solar (veja a Fig. 2.3). Pergunta: as
coordenadas dos corpos celestes mudam se mudamos o centro da Esfera Celeste?
(responda como exercício).
Fig. 2.3a – Centrando a Esfera Celeste.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
9 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.3b – Vista do céu projetada numa Esfera Celeste, de dentro para fora, centrada
em um observador na superfície terrestre.
A Fig. 2.3b apresenta a Esfera Celeste, com algumas das principais estrelas,
constelações, o equador terrestre e o Pólo Sul projetados, mais a indicação da trajetória
aparente do Sol (linha tracejada, que passa pelas chamadas Constelações do Zodíaco).
Apesar de parecer à mesma distância, por um efeito de perspectiva, as estrelas das
constelações estão na verdade distribuídas tridimensionalmente em regiões distintas no
espaço, como mostra a Fig. 2.3c.
Fig. 2.3c – Constelações: efeito de
perspectiva.
A posição de um astro qualquer na
Esfera Celeste pode ser definida sem
ambiguidade
através de dois ângulos em relação ao
sistema de coordenadas adotado, que por
sua vez é definido a partir de um ponto
central. A escolha precisa de um sistema de
coordenadas ligado à Esfera Celeste vai
depender sobretudo da análise ou problema
que se queira resolver. Para uma esfera
(qualquer uma em princípio), os sistemas de
referências utilizados são definidos por um
plano principal, que divide a esfera em duas
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
10 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
partes iguais, definindo-se assim um grande círculo (Ex: o Horizonte na Fig. 2.2; veja a Fig.
2.4 abaixo). Definimos arbitrariamente um ponto de origem neste círculo principal, por onde
passa o meridiano principal, outro grande círculo perpendicular ao grande círculo
precedente. Os (pequenos) círculos paralelos ao círculo principal definem as latitudes da
esfera, enquanto que os grandes círculos perpendiculares ao círculo principal definem as
longitudes. Estes ângulos são similares ao que utilizamos para localizar um ponto na
superfície terrestre, a longitude e a latitude.
Fig. 2.4 – Esquema de elementos gerais de um
Sistema de Coordenadas Esféricas
2.1.2 Sistema de Coordenadas Altazimutais
Fig. 2.5 – Sistema de Coordenadas Altazimutais.
Antes de introduzir o Sistema de Coordenadas Equatoriais, iremos introduzir um
outro importante sistema, o Sistema de Coordenadas Altazimutais. Este sistema (Fig. 2.5)
tem um valor prático de destaque, por ser o ideal para descrever o movimento diurno
aparente dos astros na Esfera Celeste, do ponto de vista do observador. O movimento
diurno aparente dos astros refere-se a trajetória aparente dos astros no céu, conforme a
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
11 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Terra gira em torno do seu eixo de rotação.
O plano principal do sistema de coordenadas horizontais é definido como sendo o plano
que contem o Horizonte do observador. Os dois ângulos que definem a posição de um astro
qualquer são a altura, h, e o azimute, A, como mostra a figura. O horizonte do observador
deve ser definido corretamente. O horizonte visível ou aparente é sujeito às irregularidades
topográficas, não definindo necessariamente desta forma um grande círculo e,
consequentemente, não servindo como base para a definição de um sistema de coordenadas.
Assim, definimos o horizonte astronômico como sendo o círculo centrado no observador,
perpendicular a sua vertical (definida como paralela ao campo gravitacional),
independentemente de acidentes geográficos. A intersecção desta mesma vertical com a
esfera celeste, define o Zênite e o Nadir (ponto oposto ao Zênite). A altura de um astro é
medida a partir do horizonte astronômico, sendo positivo quando o astro está acima do
horizonte e negativo no caso contrário. Assim o zênite tem por definição uma altura de 900 e o
nadir, -900. O azimute é por definição medido a partir do meridiano Sul (00) do observador e os
ângulos são contados no sentido ® Oeste (900) ® Norte (1800) ® Leste (2700). Por ser uma
definição arbitrária, o meridiano de origem do azimute é as vezes localizado no Norte, ao invés
do Sul.
Devemos notar ainda que neste sistema, as coordenadas de um astro variam com o
tempo devido sobretudo ao movimento diário (rotação da Terra). De fato, o azimute de um
astro sempre aumenta durante o decorrer de um dia (exceto pela descontinuidade a 3600).
2.1.3 Sistema de Coordenadas Equatoriais Celestes
Este sistema é uma realização muito boa de um referencial inercial, motivo pelo qual é
na prática muito utilizado até hoje. No sistema equatorial, o plano principal é a projeção do
Equador Terrestre na esfera celeste, chamado Equador Celeste (Fig. 2.5). As projeções dos
pólos terrestres na esfera celeste definem os Pólos Celestes Norte e Sul. A origem do sistema
de coordenadas é definido pela intersecção do Equador Celeste com a Eclíptica (a trajetória
aparente do Sol na esfera celeste durante um ano). Este ponto é chamado Equinócio Vernal
ou Primeiro Ponto de Áries (usamos o símbolo g ). Quando o Sol está neste ponto, temos o
início do outono no hemisfério Sul, e da primavera no Norte. Veja a Fig. 2.6a.
A Declinação, d, de um ponto M é a distância angular medida sobre o meridiano que
passa por este ponto a partir do Equador Celeste. Quando medido na direção do pólo norte
celeste d > 0, caso contrário a declinação é negativa. A Ascensão Reta, a, é o ângulo entre o
Ponto Vernal e o meridiano do astro M. A ascensão reta á medida na direção Leste. Note que a
ascensão reta cresce no sentido oposto ao azimute das coordenadas horizontais e que a
ascensão reta aumenta no sentido do movimento anual do Sol e do movimento direto do
planetas.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
12 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.6a – Sistema de Coordenadas Equatoriais Celestes. O astro M tem coordenadas
ascensão reta (a) e declinação (d). A inclinação do equador celeste em relação à Eclíptica é de
aproximadamente e = 230 26’ 21”.
Por convenção, a ascensão reta é medida um horas, minutos e segundos como o
tempo (ao invés de graus, minutos e segundos de arco). A relação é simplesmente 1h=150. A
ascensão reta e a declinação de uma estrela não se altera devido ao movimento diurno de
rotação da Terra. Isto não significa que no sistema equatorial não haja uma variação das
coordenadas com o tempo, mas esta variação é muito mais lenta que no caso das
coordenadas altazimutais.
Desde 1998, a União Astronômica Internacional (UAI), adotou um novo sistema de
referência, que é na verdade uma continuidade do Sistema de Coordenadas Equatoriais
Celestes. É o ICRS (do inglês “International Celestial Reference System”, ou Sistema
Internacional de Referência Celeste). Ele é materializado pela posição de longínquos
quasares, cuja lista com 608 objetos (ver Fig. 2.6b) é denominada de ICRF (do inglês
“International Celestial Reference Frame”, ou Rede Internacional de Referência Celeste). Essas
posições, com precisão de 1mas ou melhor, foram obtidas por milhões de observações
interferométricas na faixa rádio, usando radiotelescópios espalhados por todo o planeta.
Nas próximas seções deste Capítulo, mostraremos de forma superficial, sem entrar em
grandes detalhes, fenômenos ligados ao movimento da Terra no espaço que têm, entre outras
consequências, a de causar importantes variações nas coordenadas dos astros. Aqui, é
importante ter a noção da ordem de grandeza dessas variações, e criar uma idéia da relação
dessa ordem de grandeza com a ordem de grandeza das escalas de distância envolvidas.
Paralelamente, algumas noções de Tempo irão sendo naturalmente introduzidas, antes de
tomarmos efetivamente este tema, já no próximo Capítulo 3.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
13 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.6b – O ICRS e o ICRF.
2.2 Variação de Coordenadas Devido a Rotação da Terra
A rotação da Terra pode ser constatada por vários fenômenos, como por exemplo pelo
movimento diurno aparente do Sol ao longo do dia, que nasce no horizonte a leste e se põe a
oeste, ou pelo movimento aparente das estrelas a noite, no mesmo sentido. Aliás, esse
movimento aparente que todos os astros compartilham no céu recebe o nome indistinto de
movimento diurno.
Constata-se que leva um certo período de tempo para que a rotação da Terra se
complete para que ela dê uma volta completa em torno de seu eixo de rotação. Esse período
pode ser medido tomando-se como referência um corpo celeste qualquer e a própria Terra. Se
queremos escolher um ponto fixo como referência, podemos escolher uma estrela, já que no
período de rotação da Terra, podemos considerar que para todos os efeitos práticos uma
estrela, pela sua distância a Terra, está parada no espaço (o que, a rigor, não é verdadeiro).
Por outro lado, se queremos escolher um astro de fácil reconhecimento, de importância na
marcação do tempo na vida civil, podemos escolher o Sol. Dependendo de qual desses astros
é tomado como referência, medimos o mesmo período de rotação da Terra em escalas de
tempo diferentes, cada uma arbitrada em 24hs. Assim, tomando a estrela como referência,
temos que o período de rotação da Terra é de “24 horas siderais”. Tomando o Sol como
referência, temos que o período de rotação terrestre é de “24 horas solares”. Em outras
palavras, o período de rotação da Terra define o dia sideral (24 horas siderais) ou o dia solar
(24 horas solares), conforme o astro de referência seja respectivamente uma estrela ou o Sol.
O importante aqui é perceber que a medida do tempo, do ponto de vista da Astronomia, é feita
associando-se a passagem do tempo com configurações de astros (no caso, o alinhamento do
centro da Terra e do observador, com uma estrela ou com o Sol). Essas duas escalas de
tempo, sideral e solar, apresentam uma marcha de tempo diferente, pois as configurações
(alinhamento) dos astros estrela ou Sol repetem-se em intervalos diferentes de tempo, como
mostra a Fig. 2.7.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
14 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig 2.7 – Dia sideral e dia solar.
Se definimos como sendo 24hs solares ou um dia solar, o intervalo de tempo decorrido entre
dois alinhamentos sucessivos entre o centro da Terra, o observador e o Sol, fica fácil perceber
que o intervalo de tempo decorrido para que haja o alinhamento com a estrela é mais curto,
devido ao movimento orbital da Terra em torno do Sol e devido ao sentido da rotação da Terra
em torno se seu eixo (ambos dando-se no sentido trigonométrico, i.e., contrário ao ponteiro dos
relógios, quando vistos de cima). Assim, o dia sideral que tem 24hs siderais, quando medido
em horas solares mede 23h 56m 04s. O alinhamento com o Sol dá-se 3m 56s solares depois
de a Terra alinhar-se com a estrela. Do mesmo modo, 1 dia solar medido em horas siderais
leva 24hs 03m 56s. Se dois relógios, um marcando horas siderais outro marcando horas
solares, forem deixados funcionando, ao fim de 1 dia solar o relógio sideral estará marcando
mais 0hs 3m 56s, enquanto que ao fim de 1 dia sideral o relógio solar estará marcando 23h
56m 04s.
O movimento diurno dos astros é realmente prova da rotação da Terra? Não poderia a
Terra estar de fato parada e toda a abóboda celeste estar afinal, girando ao nosso redor? A
prova definitiva de que é a Terra que de fato gira foi dada por Galileu Galilei, ao aplicar a
experiência do Pêndulo de Foucalt em um ponto bem ao norte da Europa. Já era sabido que o
plano de oscilação do Pêndulo de Foucalt muda quando o ponto de apoio do pêndulo é
submetido a uma força externa, como o atrito por exemplo, e vice-versa, na ausência de forças
externas, o plano permanece invariante. Galileu idealizou um experimento. Construiu um
Pêndulo de Foucalt o mais próximo que podia do polo norte, garantindo dentro da capacidade
tecnológica da época que não houvesse atrito no ponto de sustentação, e garantindo um
perfeito alinhamento do prumo na vertical, em repouso. Também montou um sistema preciso
de medição da orientação do plano de oscilação. Sua hipótese era a de que, na ausência de
forças externas, a constatação de uma eventual mudança na orientação do plano de oscilação
seria a prova do giro da Terra. E foi o que de fato aconteceu. A explicação era a de que o plano
de oscilação de fato ficava parado, mas era o próprio chão que girava, e no sentido coerente
com o movimento de rotação da Terra. Evidentemente, seria no polo que o efeito seria
maximizado. O esquema da experiência é mostrado na Fig. 2.8.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
15 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.8 – Experiência com o Pêndulo de Foucault no polo: prova da rotação da Terra.
2.2.1 Marés
As marés marítimas de nosso planeta são causadas pelo desbalanço da força da
gravidade, principalmente devido à presença da Lua e em menor grau do Sol. Isto ocorre
quando consideramos as forças atuantes na metade de trás e na metade da frente da Terra,
voltada à Lua (ou Sol), lembrando que a força da gravidade é proporcional as massas, mas
inversamente proporcional a distância (veja a Fig. 2.9). Mas não são só os oceanos os únicos
constituintes de nosso planeta que podem ser deformados devido ao desbalanço gravitacional
causado pela atraçao de Lua e Sol. A crosta terrestre não é inteiramente rígida e deforma-se
também em até cerca de 15cm de altura com o efeito. O interior da Terra, sendo constituído de
um magma pastoso, com certeza também sofre os efeitos de maré.
Fig. 2.9 – As marés, como resultado da atração Gravitacional da Lua.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
16 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Devido a órbita da Lua em torno da Terra, e mesmo pela órbita da Terra em torno do
Sol, as marés tem uma natureza cíclica. O resultado é que as marés causam atrito em todos
os constituintes da Terra: magma, crosta, oceanos. Com esse atrito há dissipação de energia
cinética de rotação, resultando na diminuição da taxa de rotação da Terra em torno de seu eixo
como um todo, a uma taxa de 1,5 milisegundos/dia/século. O mesmo aconteceu com a Lua,
que foi diminuindo a sua taxa de rotação até que o seu período de rotação ficasse igual ao
período de revolução em sua órbita em torno da Terra, de cerca de 28 dias. De fato, num
futuro distante, o período de rotação da Terra tenderá a igualar-se com o período orbital da
Lua, e ambos tenderão a diminuir ainda mais a sua taxa de rotação, igualando no final seu
período de rotação com o período orbital da Terra em torno do Sol, devido a maré causada
pelo Sol.
2.3 Variação de Coordenadas Devido a Precessão e Nutação
Assim como os constituintes de nosso planeta apresentam um caráter até certo ponto
“fluido”, resultando no fenômeno da marés, não podemos esquecer que o planeta acima de
tudo apresenta características de um corpo rígido. Assim, o mesmo desbalanço gravitacional
responsável pelo fenômeno das marés, aplicado a um corpo rígido em rotação causa um
torque que faz com que o eixo de rotação, antes fixo, gire. Quando consideramos as atrações
gravitacionais de vários corpos, como o Sol, a Lua e os planetas, percebemos que o resultado
final no giro do eixo de rotação no espaço é a soma dos vários torques. Esse resultado final,
entretanto, costuma ser apresentado na forma de um somatório de várias componentes, cada
uma com amplitudes e períodos cada vez menores.
A Terra orbita o Sol num plano denominado de Eclítica. A projeção para cima, de uma
normal a Eclítica, define o polo norte da Eclítica (PNE). O eixo de rotação da Terra forma um
ângulo de aproximadamente 230 27’ com o PNE. Este ângulo é chamado de obliquidade da
Eclítica. É o mesmo ângulo formado entre a Eclítica e o Equador da Terra, projetado no
espaço. As componentes mais importantes do torque gravitacional gerado por Sol, Lua e
planetas no eixo de rotação da Terra, são chamadas de Precessão e de Nutação. As Figs.
10a,b ilustram de forma qualitativa o giro do eixo de rotação, segundo a Precessão, e o efeito
associado a Nutação. Na precessão, o eixo de rotação da Terra gira em relação ao PNE, de
forma a descrever um cone completo com ângulo de vértice igual a obliquidade da eclítica, a
cada 26 mil anos. Se imaginarmos uma linha representando a interseção entre a Eclítica e o
Equador, esta linha dá um giro completo de 26 mil anos devido a precessão, movendo-se a
uma velocidade de 51” por ano. É a Linha dos Equinócios.
Fig. 2.10a – O fenômeno da Precessão. Aqui, PN = polo norte.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
17 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.10b – Nutação. PNE = polo norte da eclítica (plano orbital da Terra ao redor do Sol)
A nutação tem como período principal o de 18,6 anos, com amplitude máxima de 9”,2
em relação ao PNE, e de 17”,2 de atraso ou adiantamento na direção da precessão.
Fig. 2.11 – Hiparco de Nicea e a descoberta da Precessão.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
18 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
A existência da precessão foi primeiramente levantada por Hipparcos, em 129 A.C. A
Fig. 2.11 ilustra como. A técnica mais precisa da época, para medir a posição de uma estrela,
era usar eclipses lunares e determinar a distância angular entre a estrela e a Lua. Usando
como origem do sistema de coordenadas a linha dos equinócios, media-se com facilidade a
longitude do Sol no plano da Eclítica (deduzida pela época da observação no ano). A longitude
da estrela era deduzida a partir das medidas entre a Lua e estrela, porque nos eclipses
lunares, a longitude da Lua era dedutível: igual a do Sol mais 1800. E mais, para astros fixos
como estrelas, a longitude teria que ser sempre a mesma. Timocharis havia medido com essa
técnica a longitude de Spica, e encontrou em 273 A.C., L=1720. Hipparcos, remedindo
observações daquele astrônomo grego, encontrou L=1740. A diferença de 2 graus não podia
ser explicada por movimento próprio da estrela, erros de medida ou de cálculo. A única
conclusão plausível era a de que a Linha dos Equinócios retrocedeu 2 graus em 144 anos.
Era constatada a existência da precessão. Somente em 1748, o astrônomo inglês Bradley
constatou a Nutação ao observar variações comuns nas coordenadas aparentes das estrelas.
A Fig. 2.12 ilustra um exemplo desse efeito na ascensão reta e declinação de Gama Draconis.
Fig. 2.12 – Bradley e a descoberta da Nutação.
2.4 Variação de Coordenadas Devido ao Movimento do Polo
Devido a movimentos e deformações da crosta terreste, a longitude e latitude terrestres
ou geográficas de um lugar podem sofrer variações. Visualmente, o fenômeno tem o efeito de
fazer parecer com que o eixo de rotação da Terra, apesar de fixo em relação ao espaço
(aproximação válida para curtos períodos de tempo), parecer “furar” o solo em pontos
diferentes, como se estivesse a deriva. Somente a posteriori a magnitude do efeito pode ser
constatada e corrigida. O efeito é importante na relação entre sistemas de coordenadas
terrestres (ou geográficos) e sistemas de coordenadas celestes. A Fig. 2.13 exemplifica o
fenômeno.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
19 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.13 – Movimento dos polos.
2.5 Variação de Coordenadas Devido ao Movimento Orbital da Terra
Fig. 2.14 – Representações do plano orbital da Terra, a Eclítica, no espaço ena representação
em Esfera Celeste (ver mais tarde uma definição de Esfera Celeste).
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
20 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
A Terra orbita o Sol, a uma distância média de 1 U.A., numa trajetória aproximadamente
circular (é, a rigor, uma elipse), num período de aproximadamente 365,25 dias solares, isto é,
passam-se aproximadamente 365,25 dias solares para a Terra completar uma volta em torno
do Sol em relação a um ponto fixo. O plano orbital da Terra em sua órbita em torno do Sol é
chamado de Plano da Eclítica, ou simplesmente, Eclítica. A linha resultante da interseção do
plano da Eclítica com o Plano do Equador, é chamada Linha dos Equinócios. Essa linha
aponta para dois sentidos. Um deles é o chamado Primeiro Ponto de Aires ou Equinócio Vernal
(g). Veja a Fig 2.14.
As estações do ano, ao contrário do que é muitas vezes propalado erroneamente em
alguns livros texto, não são causadas pela variação na distância da Terra ao Sol. A causa é o
resultado da conjugação do movimento de translação da Terra em torno do Sol com a
inclinação do eixo de rotação da Terra em relação a Eclítica (Obliquidade da Eclítica, de
aproximadamente 230,5. As configurações para Verão, Inverno, Primavera e Outono são
auto-explicativas, conforme mostrado na Fig. 2.15.
Fig. 2.15 – Estações do ano.
Que provas temos de que o movimento orbital é efetivamente da Terra ao redor do Sol,
e não o contrário? Há duas constatações que provam que de fato é a Terra que orbita o Sol.
São efeitos mensuráveis, causados por esse movimento orbital, que ocasionam variações na
posição aparente das estrelas. Esses efeitos recebem o nome de paralaxe anual e de
aberração anual.
2.5.1 Paralaxe Anual
De fato, se considerarmos a posição de uma estrela vista da Terra em um dado
instante, e 6 meses depois, verificamos que ela não é a mesma, em relação a um ponto fixo
(ponto fixo que pode ser, por exemplo, outra estrela bem mais distante). Isto não poderia
acontecer se fosse a Terra o centro do Sistema Solar, com o Sol girando em torno dela.
Somente a órbita da Terra ao redor do Sol explica essa variação. A diferença angular na
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
21 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
posição da estrela num dado instante e 6 meses depois recebe o nome de paralaxe anual.
Falaremos sobre isso de novo no Capítulo 5, pois é com medidas de paralaxe anual que se
determina de forma a mais independente possível, a distância de um astro. Nenhuma estrela
possui paralaxe maior que 1”, sendo o valor típico em geral bem menor. O efeito é ilustrado na
Fig. 2.16.
Fig. 2.16 – Distância de uma estrela medida pela paralaxe.
2.5.2 Aberração Anual
Em 1728, o astrônomo Inglês Bradley observou outro tipo de variação na posição das
estrelas, que dependia da época do ano em que fossem observadas. O efeito fazia com que a
posição de todas as estrelas aparentemente se deslocassem na direção de um mesmo ponto
no espaço, que era, na verdade, a direção para a qual a Terra se movia. O efeito é análogo ao
que observamos dentro de um carro em movimento, quando chove. Os pingos parecem
inclinados, mas se paramos o carro, verificamos que os pingos caem na horizontal. Mudança
de ventos? Não. A explicação está na relação da direção de um ponto observado, quando nos
encontramos em um referencial parado e em um referencial em movimento.
Fig. 2.17a – O fenômeno da Aberração anual.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
22 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Novamente, aqui, se a Terra estivesse imóvel, tal fenômeno não poderia ser observado. Além
disso, conforme Bradley demonstrou, a direção do desvio relacionava-se diretamente com a
direção da velocidade orbital que a Terra teria em uma órbita ao redor do Sol. A esse
fenômeno de variação na posição aparente dos astros, dá-se o nome de aberração anual. O
efeito é tal que as estrelas, em verdade, parecem descrever no céu, durante o ano, um círculo
com a forma perfeitamente proporcional a órbita da Terra (elas descrevem, a rigor, uma elipse,
já que a órbita da Terra ao redor do Sol não é perfeitamente circular). As Figs. 2.17a,b ilustram
o efeito. Seu tamanho é da ordem de 0”,3.
Fig. 2.17b – Efeito da Aberração anual na posição aparente de uma estrela.
2.6 Movimento do Sol na Galáxia
Todas as estrelas de nossa Galáxia orbitam o centro de massa, localizado em algum
ponto próximo ao centro geométrico da Via-Láctea. O Sol não é exceção. Distante cerca de
8Kpc do centro galáctico, estima-se que ele dê uma volta completa ao redor da Galáxia a cada
250 milhões de anos, próximo ao plano galáctico.
Fig. 2.18 – O Sol orbitando nossa Galáxia.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
23 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
A velocidade orbital das estrelas da Galáxia segue um padrão tal que é mais intensa
no bojo (seu centro) em menos pronunciada nos braços, havendo um ponto máximo, a partir
do qual se distingue o bojo do disco.
Fig. 2.19 – Rotação diferencial da Galáxia.
É preciso lembrar que o movimento da Terra “não pára por aí”. A nossa Galáxia está
inserida, e orbita o centro de massa, de um grupo local de Galáxias, compreendendo
distânicas da ordem de Mpcs. Este grupo, por sua vez, orbita o centro de massa de um superaglomerado bem maior, compreendendo dezenas de Mpcs, e assim sucessivamente. A medida
desses movimentos torna-se menos precisa, a medida em que as variações nas posições
desses objetos é cada vez menor, forçando o emprego de métodos indiretos de detecção
desses movimentos.
2.6.1 Sistema de Coordenadas Galácticas
Para as coordenadas galácticas, o plano principal é definido pelo plano do disco da Via
Láctea (nossa Galáxia é uma espiral, provavelmente barrada). A origem é dada pela direção do
centro galáctico, que se encontra na Constelação de Sagitário (veja Fig. 2.20). Este sistema é
utilizado normalmente em Astronomia Extragaláctica (como no estudo do grupo local de
galáxias, no qual a Via Láctea e a Galáxia de Andrômeda são seus membros principais) ou em
problemas ligados à nossa Galáxia como um todo (por exemplo, o movimento das estrelas do
disco da Via Láctea).
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
24 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.20 – Sistema de Coordenadas Galácticas. O astro M tem coordenadas longitude
galáctica (l) e latitude (b). O ponto N é a intersecção do plano galáctico com o equador celeste
(o nodo), C.G. é a direção do centro da Galáxia (que fica na constelação de Sagitário) e i é a
inclinação do plano galáctico em relação ao equador celeste.
2.7 Relação Entre Sistemas de Coordenadas
Como dissemos, existem outros sistemas de coordenadas, mais úteis que os aqui
apresentados, de acordo com o problema astronômico abordado. Por exemplo, existe o
Sistema de Coordenadas Elípticas, onde o plano fundamental é, no lugar do Equador Celeste,
o plano da Eclíptica. Este sistema é particularmente útil no estudo do movimento dos planetas
e de corpos do sistema solar que orbitam o Sol. Outro é o Sistema Horário de Coordenadas,
muito similar ao Equatorial Celeste, mas onde no lugar da Ascensão Reta, a posição é medida
em função do chamado Ângulo Horário, que mede a distância angular do astro ao meridiano
do observador.
Na maioria dos telescópios de hoje, para apontá-lo em direção ao objeto que se quer
observar, basta introduzir as coordenadas Ascensão Reta e Declinação nos círculos graduados
do instrumento, ou eventualmente o Ângulo Horário. Muitos telescópios, automatizados,
dispensam uma interferência direta do observador no instrumento, bastando fornecer por
computador as coordenadas (a,d), que o mesmo se encarrega de acionar os motores e apontar
o telescópio na direção desejada.
Foge ao nosso escopo neste Curso, demonstrar, e mesmo mostrar, as relações
matemáticas, ou fórmulas, que relacionam as coordenadas de um astro, dadas segundo dois
ou mais distintos sistemas de coordenadas. Essas relações são obtidas por Trigonometria
Esférica, ou ainda, de forma mais intuitiva, por Rotação de Matrizes.
Por outro lado, falemos de um importante aspecto que relaciona o Sistema de
Coordenadas Geográficas (latitude e longitude terrestres), o Sistema Altazimutal e o Sistema
de Coordenadas Equatoriais Celestes.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
25 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 2.21a – Movimento diurno e a visibilidade das estrelas. N = ponto cardeal norte, S = ponto
cardeal Sul, Z = Zênite, PN = polo norte, PS = polo sul. O plano da figura é o plano do
meridiano do lugar.
A Fig. 2.21a ilustra o movimento diurno de estrelas para um observador no Hemisfério
Sul. Podemos tecer interessantes conclusões a respeito dessa figura, que relaciona diversos
aspectos ligados aos 3 sistemas de coordenadas supracitados. Por exemplo, se medirmos a
altura h do polo sul (PS), obtemos a latitude geográfica f do observador. O PS é o polo
elevado porque o observador encontra-se no Hemisfério Sul. Polo elevado é um ponto
relativamente simples de ser caracterizado, pois o movimento diurno faz com que todos os
astros movam-se ao seu redor na esfera celeste (veja a Fig. 2.21b).
Fig. 2.21b – Visão da cúpula do telescópio de 1.60m do LNA, Itajubá, MG.
A foto foi feita a noite, com horas de tempo de exposição.
O plano da Fig. 2.21a é o plano do meridiano do lugar, ou simplesmente meridiano do
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
26 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
lugar, pois contém o Zênite e o polo elevado. Se medirmos a altura h de um astro quando
esse cruza o meridiano do lugar, em seu movimento diurno, obtemos a Declinação d do
astro. Pergunta: qual é a fórmula que relaciona a altura h do astro, a latitude geográfica f e
a Declinação d do astro na sua passagem pelo meridiano do lugar? (Resolva como
exercício).
Mais ainda, o próprio meridiano do lugar define os pontos cardeais Norte, Sul, Leste
e Oeste de um observador. Os pontos cardeais norte e sul resultam da intersecção do
Meridiano do Lugar e do Horizonte com a Esfera Celeste, sendo o ponto Norte aquele
voltado para o lado do Polo Norte, e o ponto Sul aquele voltado para o lado do Polo Sul. Os
pontos Leste e Oeste são definidos a partir de linhas perpendiculares a linha Norte-Sul.
Pergunta: o Sol sempre nasce no ponto cardeal Leste e sempre põe-se no ponto cardeal
Oeste? (responda como exercício).
Ainda analisando a Fig. 2.21a, podemos notar que, para um dado observador a uma
dada latitude geográfica f qualquer, nem todas as estrelas ficam visíveis. No exemplo da
figura, a partir de uma dada declinação d, nenhuma estrela ao norte do equador é visível. Por
outro lado, dentro de uma certa faixa de declinações, no Hemisfério Sul Celeste, próximas ao
polo elevado, no caso o polo Sul, todas as estrelas dessa faixa ficam visíveis: são as estrelas
circumpolares. Numa situação intermediária, há ainda aquelas estrelas que permanecem
visíveis por um determinado período, e invisíveis no outro. Pergunta 1: Dada a latitude
geográfica f de um local, deduza expressões para determinar quando uma estrela é
circumpolar, e quando é invisível, em função de sua declinação d. Pergunta 2: como
determinar a latitude f de um lugar observando a passagem meridiana de estrelas
circumpolares? (dica: use a altura h no problema). (Responda como exercício).
Fig. 2.21c – Duração do dia claro.
É interessante notar o movimento diurno do Sol, no decorrer do ano. Em função da
inclinação do eixo de rotação da Terra, o Sol cruza o meridiano do lugar em diferentes pontos
ao longo do ano. A Fig. 2.21c ilustra isso, para o Verão, Inverno e estações da Primavera e
Ountono. O fato de o Sol cruzar o meridiano do lugar em pontos distintos, faz com que a
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
27 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
duração do dia claro (Sol acima do Horizonte) seja diferente. No Verão, é maior o período de
iluminação, ao passo que no inverno, é maior a noite. Para saber se uma estrela é ou não
observável em uma data e instante qualquer, é fundamental saber se ela está acima do
Horizonte, à noite. Isso é possível, usando as expressões de visibilidade que você deduziu no
problema anterior, estabelecendo os instantes de nascer e ocaso da estrela para a data, e
finalmente, descobrindo se o Sol está abaixo do Horizonte no instante dado.
3. TEMPO
Evitaremos falar aqui de Tempo como conceito filosófico. Em Astronomia, o Tempo vale
mais pela sua materialização em escalas, de preferência uniformes, dentro do escopo da
Mecânica Newtoniana. Em relação a essas escalas, medimos outras grandezas de interesse
astrofísico.
Cada escala de tempo é definida segundo as características de seus elementos
padrão: origem, época, data, instante, intervalo de tempo, unidade, mecanismos de
contagem. A Fig. 3.1 descreve de forma intuitiva a relação entre esses elementos.
Fig. 3.1 - Escalas de tempo e seus elementos padrão: origem, época, data, instante, intervalo
de tempo, unidade, mecanismo de contagem.
Um simples relógio com seus ponteiros é um exemplo de elemento de contagem.
Porém, em Astronomia, o mecanismo clássico de contagem é fornecido pela observação das
posições aparentes das estrelas e do Sol no céu. Em particular, o Sol e a noção do dia claro e
do dia escuro, fornecem a primeira unidade de tempo que a Humanidade adotou. Veja as
várias definições de dia na Fig. 3.2.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
28 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 3.2 – Várias definições de dia.
Nas seções seguintes, serão apresentadas agora, de forma sucinta, as mais
importantes escalas de tempo usadas na Astronomia. Alguns elementos relativos a sua
definição, como dia solar e dia sideral, já foram dadas e serão reforçadas. O estudante deve
ter em mente que, como objetivo final, essas escalas de tempo buscam ser uniformes na
medida do possível, e ser reproduzíveis em quaisquer condições de observação astronômica.
Em geral, elas estão associadas ao movimento de rotação da Terra, em relação a algum ponto
de referência, como estrelas ou Sol. Para torná-las práticas ou compatíveis com a cultura civil,
muitas vezes convenções artificiais são adotadas. Veremos ao final que, devido a precisão do
mecanismo de contagem, hoje em dia o melhor padrão uniforme de tempo é o dado pelos
relógios atômicos.
3.1 Tempo Solar
Essa escala de tempo depende da rotação da Terra, e tem como referência o Sol. A
unidade de tempo, o dia solar, é definido pelo intervalo de tempo entre duas passagens
consecutivas do Sol pelo meridiano de um lugar (ver Fig. 3.3a).
O tempo civil como o conhecemos está de forma indireta relacionada a essa escala de
tempo, usando-se um Sol médio como ponto de referência, isto é, um Sol artificial que, se
existisse, equivaleria a uma Terra ideal orbitando esse Sol num círculo perfeito. Quando o Sol
médio passa pelo meridiano do lugar, é meio dia. À diferença entre o tempo solar verdadeiro
local (TQVL) e o tempo solar médio local (TQML) dá-se o nome de Equação do Tempo (Fig.
3.3b). A forma dela reflete as diferenças na velocidade orbital da Terra em sua órbita ao redor
do Sol, e a inclinação do eixo de rotação com o plano orbital (Eclítica).
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
29 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig 3.3a – Tempo Solar
Fig. 3.3b – Equação do Tempo.
3.1.1 Fusos Horários
A Hora Legal, também denominada Tempo Legal (TL) está baseada no padrão de
tempo solar médio. Ela é igual ao TQML de meridianos bem definidos, distribuídos de modo a
formar os 24 fusos horários da Terra (veja as Fig. 3.4a e b). Ela vem da necessidade de os
países estabelecerem sua hora de acordo com sua conveniência, mas respeitando convenções
que viabilizam, entre outras coisas, o transporte aéreo, marítimo e terrestre entre as nações.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
30 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 3.4a – Hora Legal e Fusos horários.
Fig. 3.4b – Hora Legal e Fusos horários no
mundo e no Brasil.
O Tempo Universal (UT, de “Universal
Time” em inglês), assim chamado, é a Hora
Legal, ou Tempo Legal TL, exatamente no
meridiano de Greenwhich, de modo que em
outro fuso horário qualquer, UT=Fuso+TL.
3.2 Tempo Sideral
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
31 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 3.5a – Tempo Sideral.
Fig. 3.5b – Relação entre Tempo Sideral e Tempo (Hora) Legal
O Tempo Sideral também é baseado na rotação da Terra, mas tendo como ponto de
referência um ponto fixo no espaço. No lugar de uma estrela, que pode ter movimento próprio,
esse ponto fixo é o Ponto Vernal (veja a Fig. 3.5a). Da mesma forma que com o Tempo Solar,
aqui temos o tempo sideral verdadeiro (TSV) e o tempo sideral médio TSM. Porém, os
significados mudam: o TSV está associado ao Ponto Vernal propriamente dito, que na verdade
move-se no espaço por causa da Precessão e Nutação, principalmente, ao passo em que o
TSM é associado a um ponto que corresponde a direção do Ponto Vernal, se apenas o termo
constante da Precessão fosse considerado. Se o Meridiano local for o de Greenwhich, temos
TSVG e TSMG, analogamente a nomenclatura do Tempo Solar. A Fig. 3.5b mostra a relação
linear que existe entre a marcha de Tempo Solar e a de Tempo Sideral médios (veja a
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
32 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
discussão de dia solar e dia sideral na página 14, Fig. 2.7).
3.3 Tempo das Efemérides e Tempo Dinâmico
Já nos anos 20 ficou claro que a escala de tempo baseada no dia solar ( e mesmo no
dia sideral) sofria de muitas irregularidades, devido à rotação terrestre, principalmente devido à
diminuição progressiva da velocidade de rotação da Terra, causada pelos efeitos de maré
luni-solar. A necessidade de uma escala mais uniforme levou ao desenvolvimento do Tempo
das Efemérides (ET) nos anos 40 e sua adoção em 1952, baseada nas equações de
movimento dos planetas e da Lua. Para tanto, foi introduzido um fator de conversão entre o
Tempo Universal UT e o Tempo das Efemérides ET (do inglês “Ephemeris Time”), tal que
DET = ET-UT, valor esse de ano em ano publicado.
O Tempo Dinâmico (TD) é a variável independente que aparece nas equações de
movimento dos corpos celestes. Na Física Newtoniana, a escala de Tempo Dinâmico é
absoluta, invariante para qualquer observador, e confunde-se com o Tempo das Efemérides
ET. Contudo, segundo a teoria da relatividade, o Tempo Dinâmico depende do sistema de
coordenadas utilizado. Assim, defini-se o Tempo Dinâmico Terrestre, TDT, referente à Terra, e
o Tempo Dinâmico Baricêntrico, TDB, referente ao baricentro do sistema solar
(aproximadamente o centro do Sol). A menos que se queira uma precisão muito alta (melhor
que um milisegundo), podemos admitir que TDT = TDB = TD.
3.4 Tempo Atômico
A definição do sistema de Tempo Atômico (TAI, de Tempo Atômico Internacional) não
está relacionado à Astronomia, mas sim à Física atômica. O tempo atômico é baseado em uma
transição hiperfina do Césio-133 (veja o esquema da Fig.3.6). Desde 1972, o TAI é utilizado
oficialmente como escala de tempo padrão, a partir da qual as outras escalas de tempo podem
ser derivadas. A grande vantagem do TAI sobre o Tempo Dinâmico é que o TAI não depende
da análise das observações dos movimentos dos astros e pode ser obtido imediatamente. Além
disso, o TAI é determinado com uma precisão de 10-12 segundos, podendo num futuro
próximo chegar a 10-14 segundos. Em 1972, quando foi introduzido, a relação entre o TAI e o
Tempo das Efemérides, ET, foi fixada da seguinte forma: ET = TAI + 32s,184 (atualmente,
utilizamos TD = TAI + 32s,184). Desta forma, a escala ‘TAI + 32,184’ pode ser considerada
como uma extensão da escala baseada no Tempo das Efemérides. Finalmente, é importante
notar que o segundo do tempo atômico foi definido de forma a ser idêntico a fração
1/31.556.925,9747 do ano trópico de 1900. Isto é, um segundo do TAI foi fixado de forma a ser
idêntico ao segundo médio medido em 1900, de acordo com a definição do segundo do
Sistema Internacional feita em 1956. Esta definição do segundo tem uma consequência
importante quando comparado com o segundo baseado na rotação da Terra (em Tempo
Universal), como veremos a seguir.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
33 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 3.6 – Padrão de frequência de relógio atômico, baseado no átomo de Césio.
3.5 Tempo Universal Coordenado
Fig. 3.7 – Relações entre as escalas de tempo uniformes TE, TD, TAI e UCT.
A partir do Tempo Atômico Internacional, definiu-se o Tempo Universal Coordenado,
UTC (do inglês “Universal Time Coordenated”). UTC é simplesmente TAI mais um número
inteiro de segundos, de modo a que a diferença entre UTC e UT1 (UT1 = UT + correções do
movimento do polo que afetam a taxa do UT), não seja nunca superior a um segundo. A
diferença entre UT1 e UTC (ou TAI) é simplesmente devido a frenagem da rotação da Terra e
das definições de segundo no TAI e no UT. Como vimos, esta desaceleração é de 1,5
milissegundos por dia por século, atualmente. Este efeito é muito pequeno e só tem um efeito
notável em intervalos de tempo geológicos. Pergunta: quantos anos levaria para que a Terra
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
34 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
girasse em torno do seu eixo no mesmo período de tempo que a Lua leva para orbitar a
Terra, isto é, 28 dias? (Resolva este exercício).
Além do mais, é muito provável que a frenagem era mais importante no passado, que
hoje. Contudo, atualmente o dia medido em Tempo Universal ganha cerca de 0,002 segundos
(de TAI) por dia. Este efeito é cumulativo e a cada 400–500 dias (ou um ano e meio)
aproximadamente, a diferença entre UT1 e UTC chega a um segundo. Disto, vem a
necessidade da introdução de um segundo a mais no ano. Este segundo é chamado segundo
intercalar (em inglês, “leap second”). Por convenção, o segundo intercalar é sempre somado ao
último segundo do mês de Junho ou Dezembro, quando necessário (ver Fig. 3.7).
Curiosamente, não temos “leap second” desde 1999, como era de se prever, o que significa
que as irregularidades na taxa de rotação da Terra foram mínimas.
3.6 Calendários
O primeiro conceito de tempo do homem, e o mais natural de todos, é o passar dos dias
e noites. Também é dos primórdios da humanidade o conhecimento do mês lunar, que se dá
com o retorno sucessivo das fases lunares. Mais tarde, em função de necessidades religiosas
surgiu o conceito de semana. O conhecimento do ano solar foi uma necessidade do homem,
quando se tornou sedentário e passou a cultivar a terra. Precisava, então, prever as estações
de chuva de seca, frio e calor, para corretamente plantar e colher.
Assim, foram então estabelecidos os calendários. Dentre os calendários históricos, os
mais importantes foram o do Egito, o da Babilônia e o da Grécia. O calendário egípcio era
somente solar, já que as preocupações desta nação eram em estabelecer corretamente as
épocas de inundação do Nilo, de semeadura e de colheita. O calendário babilônico era
luni-solar, tendo 12 meses regidos pelas fases da lua e um décimo terceiro mês em alguns
anos para se manter a correspondência com as estações do ano. O calendário grego era
também luni-solar e a inclusão do décimo terceiro mês se dava baseada nos estudos de
Meton, que viveu em Atenas por volta de 430 AC, e que verificou por meio de observações que
em 19 anos solares a lua nova voltava a ocorrer nas mesmas datas.
Os calendários modernos são o calendário Juliano e o Gregoriano. O Juliano foi
estabelecido por Julio César em Roma no ano 46 AC e estabelecia o ano de 365 dias com a
inclusão de um dia a mais a cada quatro anos, o chamado ano bissexto. O Gregoriano foi
estabelecido pelo Papa Gregório XIII em 1582, para acertar a data da páscoa em relação ao
ano tropical, uma vez que o ano tropical tem 365,242199 dias solares, sendo ligeiramente
inferior a 365,25 que é o valor médio do ano Juliano. Assim, houve uma correção de dez dias
em outubro de 1582. Isto é, ao dia 4, uma quinta-feira, seguiu-se a sexta-feira dia 15. Além
disto, a partir de então, ficou estabelecida a diminuição de três dias a cada quatro séculos da
seguinte forma: o ano final dos séculos, cujo número for divisível por quatro, será ainda assim
considerado normal, em vez de bissexto, exceto na virada dos milênios. O ano Gregoriano tem
em média 365,2425 dias, sua diferença para o ano tropical é de um dia a cada 3322,2 anos.
Como os anos não tem sempre o mesmo tamanho, para se fixar instantes separados
por grandes intervalos de tempo, os astrônomos, por sugestão de Joseph Scaliger (1540 –
1609), introduziram o chamado Período Juliano. O período juliano tem seu início fixado às 12
horas do dia 1o de janeiro de 4713 AC. A partir de então, é calculada dia a dia, a Data Juliana.
A Data Juliana 2.451.545 tem seu início às 12 horas do dia 1o de janeiro de 2000. O século
Juliano é um período de 36.525 dias julianos.
Os egípcios dividiram o dia, do nascer ao ocaso, inicialmente em quatro partes e mais
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
35 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
tarde em doze horas. A noite não era dividida. Os romanos dividiram a noite em quatro vigílias
de modo a estabelecer as trocas de guarda. Na medida em que os relógios foram adquirindo
precisão, foi que se tornou possível dividir a hora em minutos, e mais tarde, no segundo
minuto, ou simplesmente em segundos, como hoje o designamos. Essa notação hexadecimal
para o tempo, que já era adotada para as coordenadas angulares, vem dos Babilônios.
4. CATÁLOGOS ASTROMÉTRICOS
Desde que a Humanidade se reconhece como tal, isto é, há mais de pelo menos 10 mil
anos, o Homem necessitou de referências geográficas e de maneiras para contar a passagem
do tempo, para sobreviver no seu dia a dia. Com a necessidade de exploração de novos
terrenos e rotas de migração, pelos nossos ancestrais primatas, o Homem aprendeu a
assimilar aspectos do relevo, por exemplo, e aprendeu a contagem do tempo pela noção de
dia claro e da noite. Aos poucos e continuamente, foi desenvolvendo e aprimorando seus
mapas com a concepção de sistemas de referência espaciais e temporais, cada vez mais
abstratos. O grau de sofisticação dos mesmos era suficiente para atender as necessidades de
cada época do desenvolvimento de cada civilização.
Interessante notar que, nesse contexto, o uso do céu como sistema de referência, foi
universal, aparecendo em todas as civilizações da História, independentemente do grau de
complexidade das mesmas (Fig. 4.1). Com suas configurações de estrelas tão familiares
quanto eternas, acessíveis em qualquer lugar do globo, do polo norte ao polo sul, não era o
céu um mapa perfeito? Um perfeito sistema de referência? Para onde quer que o Homem
migrasse, principalmente nas longas distâncias, a atenção à localização no céu das
constelações, ou mesmo à estrelas em particular, sempre seria um guia seguro. No decorrer
do ano, a mesma atenção permitia ao Homem prever a chegada das estações, conferindo-lhe
então um sistema de contagem de tempo cíclico de escala mais longa – os primórdios de
nosso calendário.
Fig.4.1 – Registros de sistemas de referência baseados na observação do céu,
presentes em diversas civilizações antigas, no oriente e no ocidente.
4.1 Catálogos de Posição - Histórico
Na Fig. 4.1, mapas rudimentares, representativos de objetos celestes como Lua, Sol e
planetas, ilustram as primeiras tentativas de registrar a localização de astros no céu. Assim
como os mapas geográficos do Homem moderno, as representações das estrelas pelas
constelações, um dia representaram um elemento importante na História da Civilização (Fig.
4.2).
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
36 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig.4.2 – Ilustração de carta celeste “Uranometria” de Bayer, 1603.
Cerca de 4mil anos A.C., começaram a ser produzidas as primeiras tabelas com
posições de estrelas, planetas, Sol e Lua, pelas civilizações da China, da Arábia e pelos
Gregos. Essas tabelas eram grifadas em pedras ou material durável, e representam um marco.
Pela primeira vez o Homem explicitamente demonstra a importância na perpetuação e
disseminação dos registros da posição de astros no céu. Essas tabelas são os primórdios do
que hoje chamamos de catálogos astrométricos de posição. A Tabela 4.1 resume essas
primeiras tentativas bem sucedidas de registro da posição de corpos celestes.
Tabela 4.1 - Primeiras tentativas de registro de posição de corpos celestes.
Britânicos – 4000 AC (Stonehenge)
Assírios
– 3000 AC
Babilônios – 3000 AC (movimento da Lua e planetas, sistema sexagesimal)
Egípcios
– 3000 AC (posição de Polaris)
Chineses
– 700 AC (cometas, meteoros e meteorítos)
Gregos
– 650 AC (Timocaris,Tales, Pitagoras, Aristoteles, Heraclides, Aristarco)
Hiparco
– 150 AC – 850 estrelas
Ptolomeu
– 150 (DC) – Almagesto – 1030 estrelas
Chineses
– 185, 393, 1006, 1054, 1181, 1572, 1604 (supernovas)
Hindus
– 700 (sistemas de coordenadas)
Maias
– 750 (calendários)
Árabes
– 1000 (efemérides de planetas)
Astecas
– 1300 (Vênus)
Persas
– 1400 (Beg Ulugh, observações meridianas – Al Sufi, catálogo sul)
Firmicus
– 1499 – Aidus Manutius
Com relação a Tabela 4.1, é digno de nota a introdução do sistema sexagesimal dos
Babilônios, seguido pelos Gregos e até hoje empregados nos sistemas de medida angulares e
de tempo, em particular nos sistemas de coordenadas espaciais e de medida de tempo
astronômicos.
A contribuição de Hiparco de Nicea, cerca de 150AC, é também reconhecida. Ele fez
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
37 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
muitas contribuições no sentido de estabelecer elementos padrão para facilitar a descrição da
posição das estrelas no céu. Por exemplo, demonstrou a utilidade do uso de um elemento que
fica relativamente fixo no céu, uma linha imaginária definida pela trajetória aparente do Sol e
dos planetas no céu. Também descobriu a Precessão dos Equinócios. (Veremos estes
fenômenos, e a definição de outros elementos geométricos projetados no céu, mais adiante).
Finalmente, Ptolomeu em 150DC publica o Almagesto, um compêndio que tem como
maior valor a tentativa do ilustre pensador em sintetizar e sistematizar o conhecimento da
época. A posição de cerca de 1000 estrelas as mais brilhantes do céu, já era conhecida com
precisão da ordem do grau. Esta pouca precisão devia-se ao uso de instrumentos muito
rudimentares e à pouca sistematização das observações, mas era suficiente para as demandas
da época. Curiosamente, como mostra a Tabela 4.1, muitas civilizações orientais também
trabalharam no sentido de valorizar o registro da posição de estrelas em tabelas, e mesmo
civilizações na América produziram artefatos que serviam como registro astronômico e como
calendário.
A partir dos anos 1300, com as primeiras sementes do Renascentismo sendo
plantadas na Europa, e com os primeiros passos sendo dados em direção a Era das Grandes
Navegações, a Astronomia deu um grande salto no sentido de produzir tabelas de posições
cada vez mais precisas, e instrumentos cada vez melhores. Isso era necessário, para se
navegar grandes distâncias até um porto seguro, sem errar muito na sua localização. A partir
daí, a demanda por posições de estrelas mais precisas nunca parou. Ela resultou não só no
desenvolvimento de instrumentos cada vez mais robustos e mais precisos, como também
acarretou em toda uma mudança nos padrões de sistemas de coordenadas e na sistemática
das observações. E principalmente, demandou novas teorias sobre a dinâmica dos corpos
celestes. A Tabela 4.2 ilustra as principais contribuições deste período de mudanças profundas
na Astronomia.
Tabela 4.2 - Posições de corpos celestes no começo da Renascença.
Tycho Braher
– 1598, criação do sextante
Bayer
– 1603, Uranometria
Kepler
– 1606, De Stella Nova, heliocentrismo, leis do movimento
planetario
Tycho Braher teve como mérito principal a idealização e confecção de novos e precisos
instrumentos de medida da posição de estrelas e planetas no céu. Dentre eles, temos por
exemplo o enorme Círculo Vertical de mais de 27m de diâmetro. As medidas da época eram
precisas ao nível do minuto de arco. A forma sistemática de observar os astros, principalmente
os cuidados em repetir as condições metrológicas e metodológicas, conferiam ao astrônomo
alemão que morava na Bélgica, o título de melhor observador de sua geração. De fato, foram
suas observações de décadas dos planetas e do Sol, que permitiram a Kepler confirmar
definitivamente a Teoria Heliocêntrica de Copérnico, e ir um pouco além, postulando 3 leis de
movimento planetário, as famosas Leis de Kepler. Estas leis formaram um importante anteparo
para que Isaac Newton em seu Principia (1670) formulasse, com a sua a Mecânica
Newtoniana, a Lei da Gravitação Universal.
Nos séculos seguintes, com os crescentes movimentos Absolutistas, além da
crescente importância da navegação em si, agora com o Mercantilismo, devemos também
salientar a importância da demarcação dos territórios das nações européias, seja em solo
europeu, seja nas colônias por todo o mundo. É nesse período que se consolida o sistema de
coordenadas geográficas, longitude e latitude. E esse sistema de coordenadas tem relação
direta com a medida da posição das estrelas e do Sol (veremos mais detalhes a respeito em
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
38 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
outra seção mais adiante). Assim, outra motivação, agora de caráter náutico-militar, surgia no
sentido de se aprimorar ainda mais os sistemas de coordenadas empregados para descrever a
posição das estrelas no céu. A Tabela 4.3 aponta algumas das principais contribuições da
Astronomia nesse novo período.
Tabela 4.3 - Posições de corpos celestes no começo do Absolutismo.
Hevelius
– 1690 – Firmamentum
Halley
– 1712 – Southern Star Catalog
Flamsteed – 1729 – Atlas Coelestis
Lacalle
– 1752 – Table des Ascensions Droites
Messier
– 1779 – Carte Celeste
Bode
– 1801 – Uranographia
Wollaston – 1811 – A Portraiture of the Heavens
Argenlander – 1843 – Neue Uranometria
Hevelius (1690) teve o mérito de sintetizar o conhecimento da época e propor pela
primeira vez o Sistema de Coordenadas Equatoriais, cuja concepção com características de
inercialidade e de praticidade (uso em telescópios), é útil até hoje. Aqui, uma marco
importante, digno de nota, é a contribuição do astrônomo inglês Halley (o do cometa), que pela
primeira vez, concebe uma lista de posições (no sistema equatorial de Hevelius), que muito se
aproxima do que hoje chamamos de catálogo astrométrico. Também digno de nota é sua
preocupação em cobrir o céu austral, carente de observações sistemáticas. Esse problema
para a Astronomia simplesmente não existia, uma vez que os europeus não haviam colonizado
terras austrais até então.
Com o também inglês Flamsteed (1729), a determinação da posição dos astros
começa a atingir patamares de precisão nunca antes imaginados. Sua contribuição é conjugar
o telescópio ao antigo círculo vertical, tornando as medidas angulares muito mais precisas, e
para objetos de brilho muito mais fraco. Esse instrumento concebido por Flamsteed, o
chamado Círculo Meridiano, teve emprego rotineiro até recentemente no século passado. A
precisão atingida é da ordem de 2” (dois segundos de arco!). O astrônomo Messier também dá
sua contribuição, ao catalogar a posição, brilho e forma de objetos difusos, as chamadas
nebulosas de Messier, na verdade cometas, nebulosas planetárias e galáxias, dando margem
ao aparecimento de toda uma nova Cosmologia, mais tarde.
Neste período, dada a importância da Astronomia para a navegação marítima e, agora
também terrestre (definição precisa da hora nas diversas estações das malhas ferroviárias), e
dado o papel da Astronomia no mapeamento do território de uma nação, começaram a ser
montados os primeiros observatórios astronômicos do mundo, muitos dos quais existem até
hoje na Europa, nos Estados Unidos e nos demais continentes. É também no fim deste
período que definitivamente, começam a se estabelecer novas grandes áreas de estudo na
Astronomia. A Astronomia tradicional, de caráter estritamente utilitário, restrita a descrição da
posição aparente dos astros no céu, para fins geodésicos, náuticos e de cronologia do tempo,
passa a ser denominada de Astronomia Fundamental, termo que empregamos até hoje. Por
outro lado, a Mecânica Celeste e uma nova área, a Cosmologia, surgem no cenário das
ciências. É tempo dos grandes matemáticos da época começarem a dar importantíssimas
contribuições e a aprofundar as consequências da Mecânica Newtoniana ao movimento dos
corpos do sistema solar, tornando esse ramo da Astronomia, a Mecânica Celeste, um ramo
realmente distinto. Finalmente, com o desenvolvimento dos telescópios, uma série de
indagações a respeito da natureza, origem e localização de novos objetos de morfologia
intrigante (nebulosas de Messier), deu origem a um novo ramo da Astronomia, a Cosmologia.
Mais tarde, já no início do século passado, essa nova Cosmologia finalmente amadurece,
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
39 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
desdobrando-se nas outras atuais grandes áreas da Astronomia: Astrofísica Estelar, Galáctica
e Extragaláctica. Isso se deu graças ao grande desenvolvimento da Física ao longo do século
passado, com o advento da Espectroscopia, o desenvolvimento do Eletromagnetismo e com o
estabelecimento da Mecânica Quântica e da Relatividade. Aliás, a Cosmologia como hoje a
conhecemos, é agora uma grande área da Física, mas com importantes interseções com a
Astrofísica Extragaláctica.
4.2 Catálogos de Posição Modernos
Com o desenvolvimento instrumental vivido em fins do século 19 e início do século 20,
principalmente com o advento da Fotografia, já era possível observar objetos até magnitude
13. Isto envolvia basicamente estrelas e alguns poucos objetos extragalácticos, além é claro
dos planetas e alguns de seus satélites naturais. Por outro lado, o desenvolvimento das novas
áreas da Astronomia, particularmente a da Astrofísica Estelar, demandava o conhecimento
mais completo possível do maior número possível de estrelas. Isto incluía o conhecimento não
só do brilho aparente, mas também da posição aparente no céu, distância e movimento próprio
das estrelas. É em fins do século 19 e início do século 20 que os astrônomos de todo o mundo
começam a se organizar, fundando a conhecida União Astronômica Internacional (UAI, ou IAU
do inglês “International Astronomical Union). Nesse fórum, de caráter puramente científico,
decisões são tomadas com vistas a organização de grandes projetos observacionais
multinacionais.
Os projetos observacionais da UAI, traçados no início do século 20, para a
determinação das distâncias, posições aparentes e movimentos próprios para o maior número
possível de objetos do céu, são um marco para a história da Astronomia Fundamental. Não só
os clássicos Círculos Meridianos seriam utilizados, mas agora também seriam usados
telescópios refratores especialmente desenvolvidos para a tarefa, os astrógrafos, capazes de
oferecer campos fotográficos da ordem do grau quadrado, com um mínimo de distorção óptica.
A idéia era materializar um rígido sistema de referência com os Círculos Meridianos clássicos
por um lado, e por outro estender este sistema até o limite de magnitude do astrógrafo. O
conjunto de técnicas observacionais, instrumentais e de redução desenvolvidas para estes
projetos fez nascer dentro da Astronomia Fundamental um novo ramo, a Astrometria.
O resultado desses grandes projetos observacionais, foram sintetizados na forma do
que chamamos catálogos astrométricos de posição. Distintamente de outras formas de
catálogos astronômicos estelares ou de objetos de outra natureza, os catálogos astrométricos
caracterizam-se pelo extremo cuidado na obtenção da posição de seus objetos (usualmente
estrelas), isto é, caracteriza-se pelo emprego de Astrometria. Isto significa que as posições e
movimentos próprios das estrelas listadas nesses catálogos é de excelente qualidade. A
Tabela 4.4 lista os catálogos mais importantes produzidos nesses grandes projetos formulados
pela IAU (nem todos são estritamente astrométricos).
Tabela 4.4 – Catálogos de Posição - Grandes Projetos da UAI, Séculos 19/20
Bonner Durchmusterung (BD) – 1860 – 325.037 estrelas
Cape Photographic Durchmusterung (CPD) – 1896 – 450.000 estrelas
Carte du Ciel – 1890/1910 – 10.000.000 estrelas
Henry Drapper (HD) – 1924 – 225.300 estrelas
AGK1, 2, 3 – 1924 a 1963 – 500.000 estrelas
AGKR (1, ..., 3) – 1923 a 1960
Yale – 1925/1971 – 210.000 estrelas
General Catalog Boss – 1936 – 33.000 estrelas
Hamburg Sternwarfe – 1958/1975 – 265.000 estrelas
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
40 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fundamental Katalogue (FK, ..., 5) – 1923 a 1988 – 1535+3117 estrelas
Smithonian Star (SAO) Catalog – 1966 – 260.000 estrelas
Catalog of Nearby Stars (Gliese) – 1969 – 900 estrelas
Enquanto os Catálogos BD e HD (refratores comuns) foram produzidos basicamente
para obter-se de forma padronizada as magnitudes (nas bandas do visível e do azul) das
estrelas até o limite de magnitude 13, os catálogos CPD, Care du Ciel, AGK1, Yale e Hamburg
(todos com astrógrafos) serviam de base para a determinação astrométrica das posições e
movimentos próprios dessas estrelas, em todo o céu. Já os catálogos GC, e principalmente os
da série FK e AGKR (Círculo Meridiano), formavam a base, a materialização de um sistema
fundamental de referência para ser estendido aos catálogos astrográficos. Em particular, o
catálogo SAO, muito empregado nas décadas de 60 a 80 na Astronomia, é um catálogo
astrométrico de posições e movimentos próprios resultante da compilação de outros catálogos
de diferentes épocas e origens instrumentais. Essa técnica astrométrica de compilação de
catálogos é hoje em dia muito utilizada, principalmente para revitalizar catálogos antigos
dentro de novos sistemas fundamentais de referência. Cabe ressaltar também a importante
contribuição do Catálogo de Estrelas Próximas de Gliese, onde são listadas as distâncias
calculadas astrometricamente para 900 estrelas. O fato de essas estrelas estarem próximas
não é por acaso, pois a distância de uma estrela está relacionada a uma medida angular
menor que 1’’, chamada paralaxe, e em geral só pode ser obtida, com telescópios de terra,
para estrelas relativamente próximas a nós (falaremos oportunamente sobre o cálculo da
paralaxe mais tarde, em outra seção).
Em relação a época média dos catálogos astrométricos, a precisão atingida nas
coordenadas equatoriais é em geral de 0’’,05 a 0’’,10 para os catalogos fundamentais (Círculo
Meridiano), e de 0’’,3 a 1’’ para os demais (astrógrafo). Embora mais precisos, esses catálogos
fundamentais compreendem apenas um milhar de estrelas, ao passo que os astrográficos,
embora menos precisos, são da ordem de 100 vezes mais densos de estrelas. Em relação a
precisão dos movimentos próprios, ela era de 0’’,002 por ano para os catálogos fundamentais,
e de 0’’,005 a 0’’,010 por ano para os demais, se disponíveis.
Os catálogos CAMC, PPM e ACRS foram durante as décadas de 70 e 80, os principais
catálogos astrométricos usados pela comunidade astronômica, porque aliavam razoável
precisão (0’’,30 a 0’’,45) e densidade estelar. Por outro lado, a idéia de catálogo astrométrico
denso, com estrelas de magnitude maior que 13, só foi realmente realizada com a confecção
do GSC. Este catálogo foi concebido para ter pelo menos precisão de 1’’ para servir de guia ao
Telescópio Espacial Hubble. Para isso, todo o céu foi observado com Telescópios Schmidt. Os
métodos de medida empregados eram então revolucionários, com a medida das placas
fotográficas sendo feitas de maneira impessoal, com máquinas semi-automáticas chamadas
microdensitômetros. Isso sem falar no tratamento astrométrico inovador empregado às
imagens digitalizadas, que ao mesmo tempo serviam de teste de conceito às observações a
serem realizadas com a Câmara Planetária do Telescópio Hubble. Mais tarde, esses algorítmos
impessoais de medida e tratamento de dados seriam rapidamente incorporados, e até
aprimorados, à rotina de redução astrométrica nos trabalhos de alto nível dos grupos mais
ativos da área, no mundo. Não foi atoa que o advento rotineiro do detetor CCD nas
observações, a partir da década de 90, encontrou a maior parte da comunidade astrométrica já
adaptada ao seu uso. Listamos estes catálogos na Tabela 4.5.
Tabela 4.5 – Catálogos de Posição – Extensão do Sistema Fundamental até mag=16
Positions and Proper Motions (PPM) – 1991 – 378.910 estrelas
Astrographical Catalogue Reference Stars (ACRS) – 1991 – 380.000 estrelas
Carlsberg Meridian Catalogues (CAMC) – 1999 – 262.080 estrelas
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
41 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Guide Star Catalogue (GSC 1.2) – 1990 - 15.000.000 objetos
4.3 Os Novos Catálogos Astrométricos na Era HIPPARCOS
A década de 90 foi uma década de resurgimento para a Astronomia Fundamental e para
a Astrometria. É inegável o grande esforço despendido pela comunidade da Astronomia
Fundamental nos citados grandes projetos da UAI, fornecendo importantes resultados na
forma dos catálogos astrométricos em si, e principalmente em relação aos movimentos
próprios. Os esforços das décadas de 70 e de 80 em produzir catálogos mais densos e
precisos, na medida do possível, também são louváveis. Por outro lado, as demandas da
Astrofísica por dados mais precisos de distância e velocidade, para objetos cada vez mais
fracos e distantes de nós, cedo passou a não poder ser mais suprida de forma minimamente
satisfatória pela Astronomia Fundamental. Assim, em 1966 já era proposto a ESA (‘’European
Space Agency’’, ou Agência Espacial Européia em inglês) um projeto arrojado de satélite
espacial astrométrico, capaz de determinar paralaxes e movimentos próprios a uma precisão
de 0’’,001, ou 1 mili-segundo de arco, ou ainda 1mas (mas= 1 mili-segundo de arco).
Fig. 4.3 – O satélite espacial astrométrico HIPPARCOS (visto no laboratório a direita e
no momento do lançamento por um foguete Ariane, a esquerda).
Esta missão espacial de fato acabou por se realizar entre 1989 e 1993, e teve a
designação de HIPPARCOS (‘’HIgh Precision PARalax COllecting Sattelite’’, em inglês Coletor
de Alta Precisão de Paralaxes), um anacronismo em homenagem ao ilustre astrônomo Grego
Hiparco de Nicea. Dela resultou 2 catálogos, o catálogo HIPPARCOS propriamente dito, e o
catálogo TYCHO-1. A precisão de posição, paralaxe e movimento próprio para as 100mil
estrelas do catálogo ficou em 1mas, e 25 mas para as 1 milhão de estrelas do TYCHO-1.
Uma importante característica é que o catálogo HIPPARCOS é referido, de forma
indireta mas bastante confiável, a um conjunto de 610 longínquos e compactos quasares. Isso
garante, para todos os efeitos práticos, que o HIPPARCOS representa, na região ótica do
espectro eletromagnético, um sistema de referência inercial. Este conjunto de quasares
representa, na verdade, o atual sistema fundamental de referência, ICRS (do linglês
‘’Internatinal Celestial Reference System’’, ou Sistema Internacional de Referência Celeste),
adotado pela UAI desde 1998, em substituição ao antigo sistema fundamental representado
pelas séries de catálogos FK. A figura 4.4 ilustra a distribuição no céu desses quasares. As
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
42 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
posições que materializam o ICRS, vêm de medidas de interferometria com antenas rádio
dispostas em vários continentes, com precisões melhores que 1mas. Essas posições, obtidas
na faixa rádio do espectro, constituem um catálogo fundamental, chamado ICRF (do linglês
‘’Internatinal Celestial Reference Frame’’, ou Rede Internacional de Referência Celeste).
Fig. 4.4 – O ICRS, sistema fundamental de referência da UAI,
e seus representantes, os 610 quasares do ICRF.
O catálogo TYCHO-1 é, por sua vez, referido ao HIPPARCOS. A razão de sua menor
precisão em relação ao catálogo principal, vem do fato de que ele é na verdade um
sub-produto da missão, oriundo do uso de detetores secundários dispostos no satélite apenas
para sua orientação espacial. A combinação destes catálogos com outros catálogos obtidos a
partir de observações de solo, resultou na confecção de outros importantes catálogos
astrométricos da Era contemporânea, ou Era HIPPARCOS da Astronomia Fundamental: os
catálogos ACT (do inglês ‘’Astrograph Catalog – TYCHO’’) e seu sucessor, o TYCHO-2. O
quadro abaixo resume as principais características desses catálogos.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
43 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 4.4 – Cobertura observacional do catálogo UCAC em todo o céu. As faixas de baixo
para cima representam os anos de observação, desde 1999.
Novos catálogos, obtidos a partir de observações de solo, já foram produzidos em plena
Era HIPPARCOS. São mais densos e mais precisos do que seus antecessores, o PPM, o
ACRS, e mesmo o GSC. Isso por causa do próprio uso dos catálogos HIPPARCOS ou das
séries TYCHO como sistemas de referência primários, mas principalmente devido ao uso dos
detetores CCD. É o caso dos catálogos UCAC (do inglês ‘’USNO CCD Astrograph Catalog’’,
onde USNO vem de ‘’United States NavalObservatory’’). Veja o quadro de comparações acima.
O UCAC-2 já está com sua fase de observações com o astrógrafo do USNO praticamente
encerrada, como mostra a Fig 4.4. Vai até magnitude 16 como o GSC, mas com precisão de
20mas a 70mas, conforme o brilho da estrela.
Ressaltamos aqui ainda, os importantes catálogos USNO A2.0 e USNO B1, este último
publicado em 2003, resultado do uso de microdensitômetros avançados na re-redução de
antigos surveys de placas fotográficas obtidas em Telescópios Schmidt. Uma visão da
densidade de estrelas em todo o céu, em um tipo de projeção em coordenadas galácticas é
mostrado na Fig. 4.5, para o catálogo USNO-B1. São 526 milhões de estrelas até magnitude
22, com uma precisão média de 200mas.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
44 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 4.5 - Visão da densidade de estrelas em todo o céu, em um tipo de projeção em
coordenadas galácticas, para o catálogo USNO-B1. As partes mais claras são as de maior
densidade estelar.
4.4 Catálogos Astrométricos: como se apresentam e como acessá-los?
Em geral, os catálogos astrométricos listam as posições das estrelas no céu, listam a
variação dessa posição no tempo (movimentos próprios), listam a paralaxe (medida da
distância), entre outros dados, como magnitude e tipo espectral (classificação astrofísica da
estrela, que veremos em outro bloco no curso). A precisão desses valores também é
fornecida. Algumas vezes, apenas a posição (e precisão) é fornecida pelo catálogo. A Fig. 4.6
mostra o exemplo do conteúdo de um catálogo astrométrico.
Fig. 4.6 – Exemplo do conteúdo de um catálogo astrométrico, no caso, o HIPPARCOS.
Na Fig. 4.6, as 2 primerias colunas são as coordenadas no céu que indicam a posição
da estrela (o tema sistemas de coordenadas será visto mais adiante). As coordenadas foram
listadas apenas com os valores aproximados. A 3a coluna indica o movimento próprio da
estrela, isto é, a variação em segundos de arco por ano no céu da posição da estrela, causada
apenas pelo movimento no espaço da própria estrela. As demais colunas mostram o tipo
espectral, valores de magnitude, massa estimada e designação.
(*) Obs.: Linha de base entre primeira época (AC2000) e segunda (TYCHO 1
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
45 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig.4.7 – Página de abertura do banco de dados astronômicos SIMBAD, na internet.
Até bem poucas décadas atrás, antes da revolução da informática e dos computadores
pessoais, o registro dos catálogos era feito de forma impressa. Depois, em forma de fitas
magnéticas, e finalmente na forma digital como hoje a conhecemos, em arquivos de
computador. A maioria desses catálogos é distribuída pelas Universidades e Observatórios dos
centros de pesquisa em Astronomia Fundamental em todo o mundo, pela internet. Um
exemplo é o sítio do SIMBAD (ver Fig. 4.7), um banco de dados astronômicos mantido pela
Universidade de Strasburg na França (catálogos astrométricos constituem apenas uma parte
dos dados ali disponíveis). No caso de muitos catálogos astrométricos, a distribuição é feita em
CDs, como o HIPPARCOS (6 CDs), TYCHO-2 (1), UCAC(3), USNO-A2 (11), etc.
4.5 Catálogos das Futuras Missões Espaciais: Astrometria Aplicada a Astrofísica
Das futuras missões espaciais astrométricas, cujo planejamento está sendo levado a
cabo pela NASA e pela ESA, destacamos a Missão SIM e a missão GAIA. A precisão prevista,
sem precedentes, em posição, paralaxe, movimento próprio e magnitude, promete revolucionar
o quadro atual de informações cinemáticas e de brilho de nossa Galáxia e, pela primeira vez
com toda essa precisão, de nossas galáxias satélites (as Nuvens de Magalhães). Além de
expormos as características principais dessas missões (instrumental, etc), citamos também
alguns objetivos científicos pretendidos. O texto está cheio de exemplos de como a Astronomia
Fundamental e a Astrometria podem servir à Astrofísica, pelo conhecimento de distâncias
(paralaxes) e movimentos próprios. A primeira leitura desse texto é reconhecidamente difícil. O
objetivo é que o estudante retorne recursivamente a esse texto, à medida que ganhe mais
informação e conhecimento, durante este Curso, e mesmo depois dele. (algumas figuras estão
em inglês; recorra ao dicionário, e faça um curso!).
4.5.1 A Missão SIM
A missão SIM (Space Interferometry Mission) da NASA, está para entrar na 3a e última
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
46 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
fase de planejamento em 2007, com lançamento previsto para 2009, e duração de 5 anos. O
satélite SIM, através de técnicas interferométricas no ótico, e usando uma linha de base de 10
m, realizará medidas astrométricas em centenas de milhares de objetos entre magnitudes 12 <
mV < 20, com até 4 mas de erro nas posições e paralaxes trigonométricas, e 1 – 2 mas ano-1 de
erro nos movimentos próprios.
Por concepção, a operação do satélite permite observações tanto de grandes quanto de
pequenos ângulos (< 10), através de uma espécie de rede astrométrica de objetos fiduciais.
Também estão previstas a capacidade de anular imagens brilhantes, para observação dos
contornos mais fracos de objetos de interesse, e o uso de síntese de abertura para obter
imagens.
A Fig. 4.8 ilustra a planta atual do satélite. Este possui sete espelhos coletores
(siderostatos), dos quais três linhas de base arbitrárias podem ser formadas (o siderostato
extra é incluído por redundância). Duas das linhas de base são dedicadas ao controle de
estado e atitude do satélite, enquanto a terceira fornece os dados científicos. Paralelamente,
sistemas metrológicos a laser, internos e externos, monitoram as variações geométricas
relativas, por onde passa a luz.
O modo de observação do satélite é bastante diferente daquele do HIPPARCOS. Aqui, é
usada uma configuração interferométrica, bastante similar a dos experimentos Mark- III de
interferometria rádio. A variável é o tempo de atraso necessário para igualar as frentes de onda
que chegam nos dois braços interferométricos. A linha de base é monitorada pela metrologia
laser interna, durante a observação, e pela metrologia externa, entre as observações. A
redução de uma série de observações de objetos fiduciais, permite ajustar os parâmetros de
estado do caminho ótico dos feixes, além de calibrar a metrologia externa do sistema. A
solução é então utilizada para a determinação dos vetores posição dos objetos. Erros de 4 mas
de posição correspondem a precisões de 200 picometros para a linha de base de 10 m.
Fig. 4.8 – Planta atual do satélite SIM Este possui sete espelhos coletores (siderostatos), dos
quais três linhas de base arbitrárias podem ser formadas (o siderostato extra é incluído por
redundância). Duas das linhas de base são dedicadas ao controle de estado e atitude do
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
47 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
satélite, enquanto a terceira fornece os dados científicos. Paralelamente, sistemas
metrológicos a laser, internos e externos, monitoram as variações geométricas relativas, por
onde passa a luz. Os feixes são dirigidos aos detetores CCD, quando são combinados.
Os dados são então registrados e sinalizados para a Terra.
A Lei de Varredura do SIM é relativamente complexa, consistindo na observação de
pequenas curvas que vão se cruzando no céu, desde as bordas da região de exclusão do Sol,
até uma região oposta na esfera celeste, e depois executando o caminho inverso, até chegar
ao mesmo ponto de partida, 20 – 30 dias depois. Ao longo do caminho, são observados os
alvos, mais certos objetos astrometricamente fiduciais. Calcula-se que 4 ciclos completos por
ano bastam, para fechar (com os objetos fiduciais) as soluções astrométricas dos parâmetros
de calibração de estado e atitude da linha de base, ao longo do tempo, dentro das precisões
pretendidas. Isto equivale a somente 1/3 de tempo gasto. Os objetos fiduciais a serem
escolhidos não devem, em princípio, Ter manchas (“spots”), multiplicidade, companheiros
planetários, estarem sob o efeito de “microlensing”, ou apresentarem jatos relativísticos, pois
com isto seus centróides provavelmente se “agitariam” bem acima do limite de 4 mas.
Fig. 4.9 – Diagrama dos horizontes de precisão astrométrica, em termos da magnitude V, para
a missão SIM e os catálogos FK5 e HIPPARCOS.
A Figura 4.9 ilustra os horizontes de precisão astrométrica, em termos da magnitude V,
para a missão SIM e os catálogos mais precisos da atualidade, FK5 e HIPPARCOS. Baseados
nas estimativas SIM de precisão, temos que as distâncias ficariam conhecidas a 10% de erro,
dentro de 25 Kpc, e que velocidades transversais de 1 km/s a 10 Kpc ou 100 Km/s a 1 Mpc,
resultariam em movimentos próprios de 21 mas, perfeitamente detectáveis. Isto traz
importantes implicações para uma série de estudos, nas mais diversas áreas. Vamos citar
apenas algumas das possíveis contribuições do projeto SIM.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
48 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
4.5.1.1 Populações Galácticas
Essencialmente, qualquer objeto medido na Galáxia, até mV = 20, terá velocidade
transversal determinada a 1 Km/s. Assim, dentro do limite de magnitude, qualquer objeto
pertencente a quaisquer dos grupos na Galáxia, terá sua luminosidade calibrada. Os efeitos
de metalicidade e idade também poderão ser estudados para todos estes objetos,
particularmente para membros de aglomerados.
Os modelos de evolução estelar serão postos a prova, com a obtenção das distâncias
dos aglomerados galácticos e globulares.
Haverá um dramático aumento no conhecimento da função de massa, a partir das
distâncias determinadas para os sistemas binários.
As escalas de distâncias, baseadas na calibração fotométrica de luminosidades e
massas, terão grande importância para as estrelas massivas OB, AF e supergigantes M, já que
estas podem ser observadas em galáxias muito distantes. Muito provavelmente, poder-se-á
utilizar todas as Cefeidas e RR Lyrae conhecidas (principalmente as pertencentes a
aglomerados), na calibração das relações de período-luminosidade.
O satélite SIM, em medidas de pequenos ângulos (erros de 1 mas), poderia detectar
um planeta terrestre orbitando uma estrela como o Sol, a 5 pc. Assinaturas de planetas
jovianos seriam detectadas a 8 Kpc, o que corresponde a uma eficiência de detecção de 7 a 10
vezes maior que a de qualquer esquema baseado em observações de solo, para estrelas
próximas. Isto sem contar que somente os métodos astrométricos permitem a determinação
direta das massas, o parâmetro crítico em questão.
Operando no modo nulo (imagem central anulada), pode-se checar a presença de
companheiras sub-estelares, pela emissão remanescente (mesmo que térmica). Isto é
particularmente útil em casos como o de 51 Peg, onde a separação é de apenas 0,05 UA.
A investigação da dinâmica de estrelas centrais em sistemas “compactos”, tais como
aglomerados globulares, pode ser realizada com o SIM, pelo imageamento de pequenas
regiões do céu, via síntese de abertura.
4.5.1.2 Estrutura da Galáxia
As precisões do SIM permitem a determinação da cinemática e da distribuição espacial
dos diversos sub-sistemas, e da Galáxia como um todo, dentro de 25 Kpc. Devido ao
escurecimento no plano, pensa-se em dar ao SIM alguma sensibilidade no infravermelho.
O SIM permitirá a aproximação da verdadeira distribuição de tipos estelares,
melhorando a compreensão da evolução dinâmica e química da Galáxia, em particular no bojo.
A determinação do potencial gravitacional possibilitará mapear a componente Z do
campo na vizinhança solar, e em outras partes, e permitirá checar a curva de rotação,
principalmente para regiões distantes na Galáxia.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
49 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
As observações permitirão mapear as estruturas espirais de nossa Galáxia
(provavelmente assimétricas, segundo recentes estudos), dentre elas “warps” e deformações
do plano, e o tamanho e orientação da recém-descoberta barra no centro de nossa Galáxia.
Há evidências de que a recém-descoberta galáxia anã Sagitário, carrega uma cauda
que se estende a uma região de 800, do outro lado da Galáxia. O SIM pode determinar a
geometria e dinâmica das componentes desta estrutura, sendo esta uma oportunidade única
para chegar-se ao potencial galáctico a dezenas de Kpc.
4.5.1.3 Astronomia Extragalática
Com a possível exceção das Nuvens de Magalhães e da galáxia anã de Sagitário,
objetos extragaláticos encontram-se fora do alcance de medidas de paralaxe, restando a
determinação de suas velocidades transversas, dentro do limite de magnitudes.
A observação das Nuvens de Magalhães em pequenos ângulos (erros de 2 mas),
permitiria determinar distâncias a 10% de erro, levando ao mapeamento dessas galáxias em
profundidade, e permitindo a identificação de objetos interpostos entre nossa galáxia e as
satélites.
É possível, ao nível de 10 – 100 Km/s, a medida de movimentos próprios de estrelas
super-gigantes massivas, localizadas a 3 – 4 Mpc de distância. Estas estrelas deveriam ser
detectadas, em galáxias de População I significativa. Tais observações permitiriam a
constatação da cinemática desta porção do Universo, bem como traria evidências quanto às
idades do Grupo Local.
A síntese de abertura pode ser usada no mapeamento dos núcleos de AGNs,
revelando imagens 10 vezes mais resolvidas que com o telescópio Hubble, por exemplo.
Efeitos relativísticos serão testados, como a deflexão da luz, chegando-se a um
patamar tão fino, que no caso do SIM, terão que ser levados em conta não só os efeitos
causados pelo Sol, mas também os causados pelas massas de Júpiter e dos outros planetas
mais massivos.
4.5.2 A Missão GAIA
A missão GAIA (Global Astrometric Interferometer for Astrophysics), ainda na fase de
concepção de projeto, é uma das candidatas principais para o horizonte 2010+ da ESA
(Agência Espacial Européia). Está prevista para durar 5 anos. A maior parte da equipe de
astrônomos que participou da missão HIPPARCOS está envolvida no projeto. Em vários
aspectos, o projeto é uma extensão natural da missão HIPPARCOS, sendo que a
interferometria é aplicada para melhorar resolução, isto é, a precisão astrométrica. O satélite
terá dois ou quatro interferômetros óticos de grande campo, com linhas de base de alguns
metros, e operará em varredura global contínua. A meta é atingir-se precisões de 10 mas para
posições, paralaxes e movimentos próprios anuais, até o limite de completeza mV = 15 (40 - 50
milhões de estrelas). Estima-se em 350 milhões o total de objetos do catálogo, até o limite de
detecção de mV = 18. As precisões obtidas serão menores para magnitudes mV >15. A
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
50 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
fotometria multi-época será em 7 bandas. Existe a possibilidade de suplementar o satélite com
instrumentação para espectroscopia.
A Figura 4.10 ilustra o esquema dos interferômetros de Fizeau a bordo (esquerda),
bem como o mosaico de CCDs “multi-banda”, responsáveis pela detecção dos feixes
luminosos.
Para uma astrometria espacial precisa a grandes ângulos, deve-se medir ao mesmo
tempo regiões distantes no céu, tal como feito com o HIPPARCOS. No caso do GAIA, isto
poderá ser feito com um espelho duplo colimador (como antes), ou mais provavelmente serão
montados dois interferômetros com linhas de base formando um ângulo fixo entre si. O ângulo
será em torno de 600, sendo controlado por metrologia a laser. As linhas de base deverão ficar
em 2,5m. A abertura deve ficar em 0,5 m, para medir-se estrelas mais fracas. Os detetores
CCD a serem usados serão sensíveis na faixa de 350 – 800 nm, e melhorados na direção de
900 nm, pelo interesse de observações no infravermelho. As figuras de interferência são
imageadas diretamente em varredura síncrona, dispensando o uso de grades moduladoras.
Ainda há a possibilidade de se usar um prisma para medir a dispersão das franjas,
melhorando a astrometria e obtendo informação espectroscópica (baixa resolução) e
fotométrica diretamente.
Fig. 4.10 - À esquerda, uma ilustração dos interferômetros de Fizeau a bordo. À direita,
mosaico de CCDs “multi-banda”, responsáveis pela detecção dos feixes luminosos.
Algoritmos de compressão de dados, e escolha randômica de estrelas fracas, estão
sendo estudados para permitir a transmissão de dados à Terra, dentro da realidade técnica
das telecomunicações.
De forma inteiramente análoga ao HIPPARCOS, será mantido no GAIA o modo simples
de atitude orbital, evitando problemas de manobras orbitais, perturbações termais do Sol, etc.
Os grandes círculos observados devem ser fechados em poucas horas, correspondentes a
uma rotação completa do satélite em torno do seu eixo. Isto permite uma boa modelagem dos
parâmetros instrumentais (entre outros), uma vez que as condições instrumentais mudam
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
51 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
vagarosamente com o tempo.
A Lei de Varredura do GAIA seguirá na essência a do HIPPARCOS. Entretanto, ao
contrário do que ocorreu na primeira missão, a varredura será contínua, sem pré-seleção de
objetos. A grande quantidade esperada de estrelas, aliada ao aumento nas precisões, fará
aumentar consideravelmente o número de objetos não-simples (sistemas múltiplos,
variabilidades, etc.). Isto demandará o uso de modelos mais complexos, com um número bem
maior de incógnitas. A Lei de Varredura deve se amoldar a estas exigências, de forma a
maximizar o número de observações realmente independentes por objeto. A duração da
missão também deve ser cuidadosamente vista.
Além das contribuições na determinação de distâncias estelares, movimentos e
massas, a missão GAIA contribuirá com uma série de “subprodutos”, tais como informações
sobre a métrica espacial (parâmetro PPN calculado a 0,0001 %), sobre diâmetro angular de
centenas de estrelas, vasta quantidade de dados de sistemas duplos e múltiplos, estrelas
variáveis e detecção eficiente e sistemática de sistemas planetários. As precisões astrométricas
previstas, levam a determinação de distâncias (trigonométricas) com erros de 10% a 10 Kpc, e
de velocidades transversais com precisões de 1 Km/s a 20 Kpc. Assim, ao passo em que com
o HIPPARCOS apenas 0,1 % do volume da Galáxia foi alcançado, o satélite GAIA irá sondar
com medidas diretas uma grande parte da Galáxia, dentro do horizonte de paralaxes, incluindo
a maior parte do halo, e até mesmo “tocando” as Nuvens de Magalhães (ver Figura 4.11).
Outra grande conquista será o estabelecimento de um sistema de referência ótico
GAIA, em relação ao qual poderemos estudar a dinâmica dos movimentos da Terra, planetas,
Sol e do próprio sistema da Via-Láctea. Tal referencial trará grandes benefícios, como por
exemplo, no estudo da matéria escura, cujos efeitos podem se refletir em pequenos desvios
sistemáticos locais, somente detectáveis em um sistema inercial realmente preciso. A
magnitude limite é suficiente para uma conexão direta das observações com o referencial
ICRF.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
52 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 4.11 – Horizonte de distâncias para o projeto GAIA. As precisões astrométricas previstas,
levam a determinação de distâncias (trigonométricas) com erros de 10% a 10 Kpc, e de
velocidades transversais com precisões de 1 Km/s a 20 Kpc, O satélite GAIA irá sondar com
medidas diretas uma grande parte da Galáxia, incluindo a maior parte do halo, e até mesmo as
Nuvens de Magalhães.
A duração de 5 anos prevista para a missão, além de permitir o aumento natural das
precisões de posição, fornece uma base de tempo importante para os estudos da dinâmica de
asteróides, fortalece as soluções paramétricas de sistemas múltiplos e de estrelas variáveis, e
permite a detecção de planetas e de companheiras anãs marrons.
Existe uma enorme gama de aplicações para os dados GAIA em multicanal (7 bandas),
multi-época (5 anos), e de 20 mas e 20 mas ano-1 de precisão, tais como em Física e Evolução
Estelar (luminosidades estelares e idades; estrelas massivas; novas e variáveis tipo novas;
nebulosas planetárias; Cefeidas e RR Lyrae; aglomerados abertos e globulares; estrelas
pobres em metal e nucleosíntese primordial), Dinâmica de Sistemas Estelares(binárias visuais
e astrométricas; sistemas binários interagentes; binárias tipo Be emissoras de raios X; dinâmica
de aglomerados abertos e fechados), Estrutura Galáctica (dinâmica da Galáxia; sua formação;
o bojo; o halo; matéria escura no disco e no halo; a massa da Galáxia) detecção de sistemas
planetários e de anãs marrons, Astrofísica Extragalática e Relatividade Geral(escalas de
distância e idade do Universo; movimentos próprios das Nuvens de Magalhães; galáxias e
AGNs; quasares; desvio de luz pelo Sol e planetas; lentes gravitacionais e ondas
gravitacionais). A Figura 4.12 mostra os horizontes de precisão astrométrica em termos de
magnitude, para HIPPARCOS e GAIA, indicando as regiões associadas a objetos de interesse.
22/02/2010 10:46
ASTRONOMIA FUNDAMENTAL E ASTROMETRIA
53 of 53
http://pessoais.ov.ufrj.br/massaf/cursos/iam/iam2004_fundamental_arq...
Fig. 4.12 - Horizontes de precisão astrométrica em termos de magnitude, para HIPPARCOS e
GAIA. No gráfico, estão indicadas regiões associadas a alguns objetos de interesse.
22/02/2010 10:46