REVISÃO: I. O Campo Magnético
Material de Apoio de Física VII 1
REVISÃO
I – O CAMPO MAGNÉTICO
Os exercícios a seguir foram extraídos dos livros recomendados no curso (Ver Referências [1, 2, 3, 4] na
Apresentação). Eles estão organizados de tal forma que podem ser impressos em A4 frente e verso.
FORMULÁRIO E TABELA
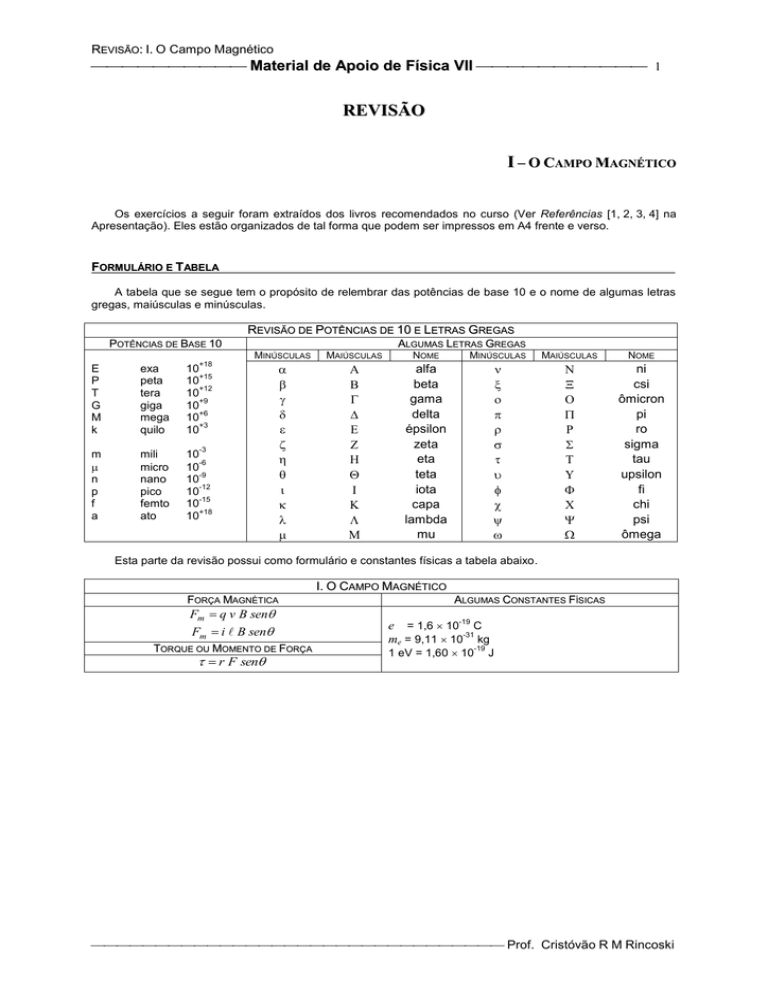
A tabela que se segue tem o propósito de relembrar das potências de base 10 e o nome de algumas letras
gregas, maiúsculas e minúsculas.
REVISÃO DE POTÊNCIAS DE 10 E LETRAS GREGAS
POTÊNCIAS DE BASE 10
ALGUMAS LETRAS GREGAS
MINÚSCULAS
MAIÚSCULAS
NOME
MINÚSCULAS
MAIÚSCULAS
NOME
alfa
beta
gama
delta
épsilon
zeta
eta
teta
iota
capa
lambda
mu
ni
csi
ômicron
pi
ro
sigma
tau
upsilon
fi
chi
psi
ômega
+18
E
P
T
G
M
k
exa
peta
tera
giga
mega
quilo
10
+15
10
+12
10
+9
10
+6
10
+3
10
m
n
p
f
a
mili
micro
nano
pico
femto
ato
10
-6
10
-9
10
-12
10
-15
10
+18
10
-3
Esta parte da revisão possui como formulário e constantes físicas a tabela abaixo.
I. O CAMPO MAGNÉTICO
FORÇA MAGNÉTICA
Fm q v B sen
Fm i B sen
TORQUE OU MOMENTO DE FORÇA
r F sen
ALGUMAS CONSTANTES FÍSICAS
e = 1,6 10-19 C
me = 9,11 10-31 kg
1 eV = 1,60 10
-19
J
Prof. CristóvãoRMRincoski
REVISÃO: I. O Campo Magnético
Material de Apoio de Física VII 2
LISTA DE EXERCÍCIOS 1 (15R)
Atenção:
Montar uma equipe de 4 ou 5 alunos e faça os exercícios abaixo.
Aluno:
Aluno:
Aluno:
Aluno:
Aluno:
1.
Turma:
Turma:
Turma:
Turma:
Turma:
Data:
Data:
Data:
Data:
Data:
/
/
/
/
/
/
/
/
/
/
a
(3R) Baseado no Ex.: 1. pág. 175, Halliday, 4 ed.
(3R) Na fórmula Fm q v B sen , (a) representa um ângulo entre quais vetores? (b) Dos três vetores
F m , v e B quais pares são sempre perpendiculares? (c) Que pares podem formar um ângulo diferente de
0
90 entre si?
R.:
2.
a
(1R) Baseado no Ex.: 3E) pág. 176, Halliday, 4 ed.
-19
6
(1R) Um elétron (e = –1,60 10 C), num antigo tubo de imagem de TV, movia-se a 7,20 10 m/s num
-3
campo magnético de aproximadamente 83,00 10 T. Sem conhecermos a direção do campo magnético,
quais são o maior e o menor módulo da força que o elétron pode sentir neste campo?
R.:
3.
a
(2R) Baseado no Ex.: 11E) pág. 177, Halliday, 4 ed.
(2R) Um campo elétrico de 1,50 kV/m e um campo magnético de 0,400 mT atuam sobre um elétron em
0
movimento de modo a produzir uma força nula. Supondo = 90 (a) calcule a velocidade escalar mínima do
elétron. (b) Como devem estar os campos elétrico e magnético para que isto aconteça ( Fe Fm )?
R.:
4.
a
(2R) Baseado no Ex.: 35P) pág. 179, Halliday, 4 ed.
-19
(2R) Um pósitron com energia cinética de 2,0 keV (1 eV = 1,60 10 J) é projetado para dentro de um
campo magnético uniforme de 0,10 T, com o seu vetor velocidade fazendo um ângulo de 45º com o campo
7
magnético. Supondo a velocidade do pósitron seja v = 2,65 10 m/s, determine (a) a massa do pósitron
(ela confere com a afirmação abaixo?) (b) o módulo da força magnética que atua no pósitron.
-19
(NP)
“Um pósitron possui a mesma massa que o elétron, mas a carga elétrica é positiva = +1,60 10 C” .
R.:
(NP)
Nota do Professor
Prof. CristóvãoRMRincoski
REVISÃO: I. O Campo Magnético
Material de Apoio de Física VII 3
5.
a
(2R) Baseado no Ex.: 2) pág.489, Alberto Gaspar, 1 ed.
(2R) Os ímãs abaixo (Fig. 1) estão marcados com letras nas extremidades (de A até F). Como não se sabe
a polaridade dos ímãs, (a) Como fazer para atribuir polos (Norte ou Sul) para cada ímã? (b) Se A for polo Sul
qual será o polo do resto dos ímãs? (Obs.: os ímãs se atraem de acordo com BC e DE).
A
B
C
Barra 1
D
E
F
Barra 3
Barra 2
Fig. 1
R.:
6.
a
(2R) Baseado no Ex.: 3) pág.489, Alberto Gaspar, 1 ed.
(2R) O ímã abaixo (Fig. 2) foi cortado em várias partes, como indicado pela linha tracejada. (a) Quantos
ímãs serão formados? (b) Qual será a polaridade de cada uma das partes separadamente?
N
S
Fig. 2
R.:
7.
a
(3R) Baseado no Ex.: 23) pág.174, Serway, 3 ed.
(3R) Uma bobina retangular é constituída por 100 espiras (Fig.
3), tem as dimensões 0,4 m por 0,3 m e é percorrida por uma
corrente de 1,2 A. A bobinha está articulada no eixo y, e seu
plano faz um ângulo de 30º com o eixo x. (a) Qual a força
exercida em cada uma dos lados da bobina, se o campo
magnético está alinhado com o eixo x e é igual a 0,8 T? (b)
Qual é o torque (ou momento de força) calculado no ponto
central de cada lado da bobinha, devido à interação entre o
campo magnético e a corrente que percorre a bobina? (c) Qual a
direção que se pode esperar para rotação da bobina?
y
i = 1,2 A
0,4m
x
30º
0,3m
R.:
z
Fig. 3
Prof. CristóvãoRMRincoski
REVISÃO: I. O Campo Magnético
Material de Apoio de Física VII 4
LISTA DE EXERCÍCIOS 1: EXERCÍCIOS COMPLEMENTARES
1.
v
B
+
q
B
a
(1R) Ex.: 6) pág. 490, Alberto Gaspar, 1 ed.
(1R) (PUC–MG) Uma carga +q, com velocidade
v , desloca-se em um
campo magnético B . A carga sofre uma força magnética
F
de módulo
F q v B ; Fig. 1, a direção e o sentido dessa força estão adequadamente
representados em:
Fig. 1
a)
2.
b)
c)
a
(1R) Ex.: 7) pág. 490, Alberto Gaspar, 1 ed.
(1R) (Vunesp) Em determinada região do espaço, há um campo
magnético uniforme ( B ), de direção perpendicular ao plano da
figura e sentido apontado para os olhos do observador, como
indica a Fig. 2. Um corpo carregado negativamente é lançado
nesse campo na direção e sentido indicados pela seta 3 da
figura. A trajetória descrita por esse corpo é representada pelo
número:
a) 1.
d) 4.
b) 2.
e) 5.
c) 3.
3.
4.
3
1
5
2
Fig. 2
4
a
(1R) Ex.: 13) pág. 491, Alberto Gaspar, 1 ed.
(1R) (Vunesp) Uma partícula positivamente carregada com carga de
20 C penetra perpendicularmente em um campo magnético uniforme,
4
de intensidade 4,0 T, com velocidade de 1,0 10 m/s, conforme a
figura 3. A intensidade da força magnética a que a partícula fica sujeita
tem, valor em newtons, igual a:
a) 0,1.
d) 0,6.
b) 0,2.
e) 0,8.
c) 0,3.
(1R) – Rafael
(1R) (FEEVALE RS/2001) A Figura 4 mostra um campo magnético
uniforme, perpendicular ao plano da página, com sentido entrando na
página.
A direção e o sentido da força magnética que atua na carga q, positiva,
que se movimenta com velocidade v em relação ao campo, serão
a) paralelo ao plano da página, para cima.
b) paralelo ao plano da página, para baixo.
c) paralelo ao plano da página, para esquerda.
d) paralelo ao plano da página, para direita.
e) perpendicular ao plano da página, para dentro.
5.
d)
B
v
+
q
Fig. 3
Fig. 4
(1R) – Rafael
(1R) (UDESC/2010/Janeiro) Os fornos de micro-ondas usam um gerador do tipo magnetron para produzir
9
micro-ondas em uma frequência de aproximadamente 2,45 GHz (2,4510 Hz). Ondas eletromagnéticas
desta frequência são fortemente absorvidas pelas moléculas de água, tornando-as particularmente úteis
para aquecer e cozinhar alimentos. Em um experimento em laboratório, deseja-se mover elétrons em órbitas
circulares com a frequência de 2,45 GHz, usando um campo magnético.
Assinale a alternativa que representa corretamente o valor do módulo do campo magnético necessário para
que isso ocorra.
21
–21
a) 2,710 T.
d) 8,710 T.
Prof. CristóvãoRMRincoski
REVISÃO: I. O Campo Magnético
Material de Apoio de Física VII 5
–2
b) 8,710 T.
–20
c) 2,310 T.
6.
2
e) 2,710 T.
(1R) – Rafael
(1R) (UEL PR/1999/Janeiro - Adaptada) Uma partícula com carga elétrica
4
1 C penetra num campo magnético de 5T, com velocidade de 210 m/s,
perpendicular ao campo de indução magnética. A velocidade faz um ângulo
de 30º conforme mostrado na Figura 5. A partícula ficará sujeita a uma força
magnética de módulo igual a:
–1
–2
a) 110 N.
d) 110 N.
–2
b) 510 N.
e) 5 N.
–1
c) 510 N.
B
v
300
+
q
Fig. 5
Prof. CristóvãoRMRincoski
REVISÃO: II. Corrente Elétrica e Campo Magnético
Material de Apoio de Física VII 6
REVISÃO
II – CORRENTE ELÉTRICA E CAMPO MAGNÉTICO
FORMULÁRIO E TABELA
Esta parte da revisão possui como formulário a tabela abaixo.
II. CORRENTE ELÉTRICA E CAMPO MAGNÉTICO
LEI DE AMPÈRE
ALGUMAS CONSTANTES FÍSICAS
B cos 0 i
CAMPO MAGNÉTICO DE UM FIO INFINITO
B
0 i
2 r
FORÇA MAGNÉTICA ENTRE DOIS FIOS PARALELOS
Fm
0 i1 i 2
2 d
0 = 4 10 T m/A
-12
2
2
0 = 8,85 10 C /Nm
-7
CAMPO MAGNÉTICO DA ESPIRA / BOBINA
Be
0 i
2r
e
Bb
0 N i
2r
CAMPO MAGNÉTICO DO SOLENÓIDE
Bs
0 N i
ou
Bs 0 n i com n
N
Prof. CristóvãoRMRincoski
REVISÃO: II. Corrente Elétrica e Campo Magnético
Material de Apoio de Física VII 7
LISTA DE EXERCÍCIOS 2 (10R)
Atenção:
Montar uma equipe de 4 ou 5 alunos e faça os exercícios abaixo.
Aluno:
Aluno:
Aluno:
Aluno:
Aluno:
1.
Turma:
Turma:
Turma:
Turma:
Turma:
/
/
/
/
/
/
/
/
/
/
a
(1R) Ex.: 5. pág. 503, Gaspar, 1 ed.
(1R) (Ufac) Um fio reto infinito é percorrido por uma corrente elétrica i, observando-se em um ponto P um
campo magnético de módulo B associado à corrente i. Se a corrente elétrica no fio for triplicada, então o
módulo do campo magnético observado no ponto P será:
B/3.
B/2.
3 B.
B.
4 B.
a)
b)
c)
d)
e)
2.
Data:
Data:
Data:
Data:
Data:
a
(1R) Ex.: 7. pág. 504, Gaspar, 1 ed.
(1R) (UFMG) Na Fig. 1 estão representados dois fios, percorridos por correntes
elétricas de mesma intensidade e de sentidos contrários e dois pontos, K e L.
Os fios e os pontos estão no mesmo plano. O ponto L é eqüidistante dos dois fios e o
ponto K está à esquerda deles. Considerando estas informações, é correto afirmar que
o campo magnético:
a)
b)
c)
d)
em
em
em
em
K, é nulo e, em L , está entrando no papel.
K, está entrando no papel e, em L, está saindo dele.
K, está saindo do papel e, em L, é nulo.
K, está saindo do papel e, em L, está entrando nele.
K
L
Fig. 1
3.
a
(1R) Ex.: 14. pág. 504, Gaspar, 1 ed.
(1R) (Uece) A Fig. 2 mostra uma pequena agulha magnética colocada no interior de um solenoide. Com a
chave C desligada a agulha tem a orientação mostrada na figura. Ao ligar a chave C obtemos no interior
do solenoide um campo muito maior que o campo magnético terrestre.
N
N
a)
c)
N
S
S
S
N
b)
d)
S
C
N
Fig. 2
S
4.
R
+
a
(2R) Baseado no Ex.: 10E) pág. 198, Halliday, 4 ed.
(2R) Um condutor retilíneo transportando uma corrente i, é dividido em voltas
semicirculares idênticas, como é mostrado na Fig. 3. (a) Qual é o campo
magnético resultante no centro C da espira circular? (b) Se pudéssemos
invertemos o sentido da corrente no arco inferior, o que aconteceria com o
campo magnético?
i
C
i
Fig. 3
R.:
Prof. CristóvãoRMRincoski
REVISÃO: II. Corrente Elétrica e Campo Magnético
Material de Apoio de Física VII 8
5.
a
(2R) Baseado no Ex.: 5) pág.204, Serway, 3 ed.
(2R) Um condutor, com a forma de uma espira quadrada com lado l = 0,4 m, tem uma
corrente i = 10 A (Fig. 4). (a) Calcular o módulo e a direção do campo magnético no
centro do quadrado. (b) Se trocarmos a espira quadrada por uma circular (de mesmo
comprimento, ou perímetro e percorrida pela mesma corrente), qual o valor do campo
magnético no centro desta nova espira?
R.:
i
l
Fig. 4
30 A
6.
R.:
7.
a
(2R) Baseado no Ex.: 38P) pág. 201, Halliday, 4 ed.
(2R) Na Fig. 5, o fio retilíneo longo transporta uma corrente de 30 A e a
espira retangular transporta uma corrente de 20 A. (a) Em quais fios da
espira retangular teremos força magnética? (b) Calcular a força resultante
atuando sobre a espira. Suponha que a = 1,0 cm, b = 8,0 cm e L = 30
cm.
20 A
a
b
20 A
L
Fig. 5
(1R)
(1R) Um solenoide de comprimento l = 10 cm, é percorrido por uma corrente i = 10 A. Qual deve ser o
número de espiras para que o campo magnético no eixo central do solenoide seja da ordem de 1,2 T?
(Dica: considerar como solenoide ideal, ou infinito).
R.:
Prof. CristóvãoRMRincoski
REVISÃO: II. Corrente Elétrica e Campo Magnético
Material de Apoio de Física VII 9
LISTA DE EXERCÍCIOS 2: EXERCÍCIOS COMPLEMENTARES
1.
2.
a
(1R) Ex.: 9) pág. 504, Alberto Gaspar, 1 ed.
(1R) (Furg–RS) Dois fios paralelos e próximos, A e B, têm
correntes i e 3i de mesmo sentido. Com relação às forças que
cada fio exerce um sobre o outro, podemos afirmar que:
a) os fios exercem forças repulsivas de igual magnitude um
sobre o outro.
b) os fios exercem forças atrativas de igual magnitude um
sobre o outro.
c) os fios não exercem forças um sobre o outro.
d) o fio A exerce uma força maior sobre o fio B do que o fio
B exerce sobre o fio A.
e) o fio B exerce uma força maior sobre o fio A do que o fio
A exerce sobre o fio B.
3i
i
Fig. 1
a
b)
c)
d)
4.
B
(1R) Ex.: 11) pág. 504, Alberto Gaspar, 1 ed.
(1R) (Ufop–MG) Uma bússola é colocada no ponto C localizado no interior de uma
espira ligada a uma bateria, como mostra a Fig. 2.
Então é correto afirmar que a agulha da bússola vai se orientar:
a)
3.
A
C
segundo a normal ao plano da espira, com o pólo norte dirigido da espira para o
leitor.
segundo a reta vertical localizada no plano da espira, com o pólo norte dirigido para
cima.
segundo a normal ao plano da espira, com o pólo norte dirigido do leitor para a
espira.
segundo a reta vertical localizada no plano da espira, com o pólo norte dirigido para
baixo.
+
Bateria
Fig. 2
a
(1R) Ex.: 13) pág. 505, Alberto Gaspar, 1 ed.
(1R) (ITA-SP) Uma espira circular de raio R é percorrida por
uma corrente i. A uma distância 2R de seu centro, encontra-se
um condutor retilíneo, muito longo, que é percorrido por uma
corrente i1 (conforme figura 3). As condições que permitem que
se anule o campo de indução magnética no centro da espira são,
respectivamente:
a)
i1
b)
i1
c)
i1
d)
i1
e)
i1
i
i
i
i
i
i1
2R
R
2 e a corrente na espira no sentido horário.
2 e a corrente na espira no sentido anti-horário.
Fig. 3
e a corrente na espira no sentido horário.
e a corrente na espira no sentido anti-horário.
2 e a corrente na espira no sentido horário.
(1R) – Rafael
(1R) (UFPel RS/2006/Julho) A figura 4 representa um fio retilíneo e
muito longo percorrido por uma corrente elétrica convencional i, de A
para B.
Com relação ao sentido do campo magnético criado pela corrente
elétrica no ponto P e a sua intensidade, é correto afirmar que:
a) o sentido é para fora da página e sua intensidade depende da
2
distância “r ”.
b) o sentido é para o ponto “1” e sua intensidade depende da
distância “r”.
c) o sentido é para o ponto “2” e sua intensidade independe da
distância “r”.
d) o sentido é para dentro da página e sua intensidade depende da
Fig. 4
Prof. CristóvãoRMRincoski
REVISÃO: II. Corrente Elétrica e Campo Magnético
Material de Apoio de Física VII 10
distância “r”.
e) o sentido é para o ponto “3” e sua intensidade depende de “i” e independe de “r”.
5.
(1R) – Rafael
(1R) (FURG RS/2003) Uma corrente constante i passa em cada um dos três
fios retilíneos longos, situados nos vértices de um triangulo equilátero. Os
fios são normais em relação ao plano que contém o triângulo, conforme
mostra a Figura 5.
Desconsiderando o campo magnético terrestre, a orientação de uma bússola
colocada no ponto P é:
a)
6.
b)
c)
d)
e)
Fig. 5
(1R) – Rafael
(1R) (UDESC/2011/Julho) A força entre dois fios condutores paralelos, perpendiculares ao plano da página,
ambos com 10,0 m de comprimento e separados por 5,00 cm, é de repulsão. A corrente elétrica em ambos é
de 20,0 A.
A alternativa que melhor representa a força é:
a)
d)
b)
e)
c)
7.
(1R) – Rafael
(1R) (PUC RS/1999/Julho - Adaptado) Um fio condutor em forma de solenoide (Figura 6a) encontra-se no
interior de um campo magnético uniforme, variável no tempo segundo a função B(t) – abaixo representada
(Figura 6b).
Fig. 6a
Fig. 6b
2
Supondo-se que o fio tem 10 espiras e cada espira tem área de 0,002 m , perpendicular às linhas do campo,
o valor absoluto da diferença de potencial induzida entre os extremos do fio durante o intervalo de tempo de
-3
zero a 2,010 s vale:
a) 0,5 volt.
b) 1,0 volt.
c) 2,5 volts.
d) 3,5 volts.
e) 5,0 volts.
Prof. CristóvãoRMRincoski
REVISÃO: III. Indução Eletromagnética
Material de Apoio de Física VII 11
REVISÃO
III – INDUÇÃO ELETROMAGNÉTICA
FORMULÁRIO E TABELA
Esta parte da revisão possui como formulário a tabela abaixo.
III. INDUÇÃO ELETROMAGNÉTICA
FLUXO MAGNÉTICO
ALGUMAS CONSTANTES FÍSICAS
B B S cos
L E I DA IND UÇÃ O DE F A RA DA Y
B
t
ou N
B
t
FORÇA ELETROMOTRIZ INDUZIDA
B S sen( t )
N B S sen( t )
FORÇA ELETROMOTRIZ E CORRENTE NUM TRANSFORMADOR
1 N1
i
N
, 2 1
i1 N 2
2 N2
e
1 i2
2 i1
Prof. CristóvãoRMRincoski
REVISÃO: III. Indução Eletromagnética
Material de Apoio de Física VII 12
LISTA DE EXERCÍCIOS 3 (12R)
Atenção:
Montar uma equipe de 4 ou 5 alunos e faça os exercícios abaixo.
Aluno:
Aluno:
Aluno:
Aluno:
Aluno:
1.
Turma:
Turma:
Turma:
Turma:
Turma:
Data:
Data:
Data:
Data:
Data:
/
/
/
/
/
/
/
/
/
/
a
(1R) Ex.: 3. pág. 517, Gaspar, 1 ed.
(1R) (Ufam/PSC) Um ímã desloca-se da esquerda para a direita com velocidade constante, ao longo de
uma linha que passa pelo centro de uma espira metálica fixa, perpendicularmente ao plano desta. A e B
representam os sentidos anti-horário e horário, respectivamente, visto por um observador sobre o ímã ao se
aproximar da espira, como mostra a Fig. 1. Sobre a corrente elétrica na espira, podemos afirmar que:
a)
b)
c)
d)
e)
tem o sentido de B quando o ímã se aproxima e A
ímã se afasta da espira.
tem o sentido de A quando o ímã se aproxima ou
da espira.
tem o sentido de A quando o ímã se aproxima e B
ímã se afasta da espira.
tem o sentido de B quando o ímã se aproxima ou
da espira.
é sempre nula.
A
quando o
se afasta
v
quando o
S
N
se afasta
Fig. 1
B
2.
a
(6R) Ex.: 11. pág. 519, Gaspar, 1 ed.
(6R) (UEM-PR) Uma espira condutora, mostrada na FIg. 2, está penetrando em uma região onde existe um
campo magnético B = 0,5T, perpendicular e entrando no plano, com velocidade constante v = 10 m/s,
passando sucessivamente pelas posições 1, 2 e 3. Nestas condições, assinale o que for correto.
1
10cm
20cm
B (entrando)
v
2
v
3
v
Fig. 2
01. Quando a espira está passando pela posição 1, o fluxo magnético através dela está aumentando.
-2
2
02. Quando a espira está passando pela posição 2, o fluxo magnético através dela é de 1,0 10 T m .
04. A fem induzida na espira na posição 2 é de 0,5 V.
08. O sentido da corrente induzida na espira é o mesmo, tanto na posição 1 como na posição 3.
16. Se a espira tem resistência de 2,0 , a corrente induzida na espira é de 0,25 A na posição 3.
32. Na posição 3 a corrente induzida possui sentido anti-horário.
Dê como resposta a soma dos números associados às afirmações corretas.
3.
a
(1R) Ex.: 15. pág. 520, Gaspar, 1 ed.
(1R) (UFRN) A linha telefônica fixa residencial é movida a corrente elétrica contínua (CC), com tensão de
45 V, e funciona de forma independente da rede elétrica convencional, que é de corrente alternada (CA) e
(NP)
com tensão de 220 V . Devido a uma freqüente falta de energia na linha convencional de sua casa,
Joãozinho, estudante do ensino médio, pensou em fazer um transformador elevador de tensão para usar na
luminária de sua mesa de estudo. Sua idéia é tirar a energia da tomada do telefone (o que é proibido por lei)
e usá-la em uma situação de emergência. Pode-se dizer que o objetivo de Joãozinho:
a)
(NP)
será alcançado, mas pela Lei de Faraday, o rendimento da luminária cairá um pouco em relação àquele
obtido quando a luminária é ligada na rede convencional.
A tensão fornecida pela COPEL é de 127 V ou 220 V, normalmente 127 V.
Prof. CristóvãoRMRincoski
REVISÃO: III. Indução Eletromagnética
Material de Apoio de Física VII 13
b)
c)
d)
4.
só será alcançado se a linha telefônica tiver tensão de, pelo menos, 110 V.
não será alcançado pela impossibilidade de se elevar uma tensão contínua para tensão alternada
somente com um transformador.
não será alcançado porque tensão só pode ser baixada e não elevada.
a
(1R) Baseado no Ex.: 39) pág.232, Serway, 3 ed.
(1R) Uma bobina quadrada (20 cm 20 cm) é constituída por 100 espiras de fio
condutor e gira em torno de um eixo vertical, a 1500 rpm, com mostra a Fig. 3. A
componente horizontal do campo magnético terrestre, na região onde está a bobina, é 2
-5
10 T. Calcular a fem máxima induzida na bobina pelo campo da Terra. (Dica: a fem
máxima se dá quando o sen() possui valor máximo).
R.:
Fig. 3
5.
a
(1R) Baseado no Ex.: 40) pág.232, Serway, 3 ed.
(1R) Uma bobina circular de 400 espiras e com o raio de 15 cm gira em torno de um eixo perpendicular a
um campo magnético de 0,2 T. Qual a velocidade angular que provocará uma fem máxima induzida de
4 V?
R.:
= 57º
6.
a
(1R) Baseado no Ex.: 1E) pág. 223, Halliday, 4 ed.
(1R) Num certo local do hemisfério norte, o campo magnético da Terra
tem módulo de 42 T e aponta para baixo, formando um ângulo de 57º
com a vertical. Calcular o fluxo através de uma superfície horizontal de
2
área igual a 2,5 cm ; veja a Fig. 4, na qual o vetor normal de área, de S,
foi arbitrariamente escolhida para baixo.
R.:
n
Fig. 4
Prof. CristóvãoRMRincoski
REVISÃO: III. Indução Eletromagnética
Material de Apoio de Física VII 14
7.
a
(1R) Baseado no Ex.: 3E) pág. 223, Halliday, 4 ed.
(1R) Uma antena circular de televisão para UHF (Ultra High Frequency – frequência ultraelevada) tem
diâmetro de 11 cm. O campo magnético de um sinal de TV é normal ao plano da antena, e num dado
instante, seu módulo está variando na taxa de 0,16 T/s. O campo magnético é uniforme. Qual a fem
induzida na antena? (Dica: foi dado
B
).
t
R.:
Prof. CristóvãoRMRincoski
REVISÃO: III. Indução Eletromagnética
Material de Apoio de Física VII 15
LISTA DE EXERCÍCIOS 3: EXERCÍCIOS COMPLEMENTARES
1.
a
(1R) Ex.: 5) pág. 518, Alberto Gaspar, 1 ed.
(1R) (Ufes) A Fig. 7 mostra um ímã movendo-se com
velocidade constante v , ao longo do eixo que passa
pelo
centro
de
uma
espira
retangular,
perpendicularmente a seu plano. A espira é formada por
um fio condutor e por uma resistência R.
v
R
N
S
B
Fig. 7
A
O pólo norte do ímã está voltado para a espira enquanto o ímã estiver aproximando-se da espira, é correto
afirmar que a corrente induzida nela é:
a) nula, porque a espira é retangular.
b) nula, porque a velocidade do ímã é constante.
c) diferente de zero, mas o seu sentido não pode ser determinado.
d) diferente de zero, e seu sentido, através da resistência é de A para B.
e) diferente de zero, e seu sentido, através da resistência é de B para A.
2.
a
(1R) Ex.: 7) pág. 518, Alberto Gaspar, 1 ed.
(1R) (UFV-MG) Próximo a um fio percorrido por uma
corrente i são colocadas três espiras, A, B e C,
como mostra a figura 8.
Se a corrente no fio aumenta com o tempo, pode-se
afirmar que os sentidos da corrente induzida nas
espiras A, B e C, respectivamente são:
a)
b)
c)
d)
e)
3.
B
i
C
Fig. 8
a
(1R) Ex.: 8) pág. 519, Alberto Gaspar, 1 ed.
(1R) (UFSM-RS) Se o campo magnético que passa através da espira aumenta
uniformemente com o tempo, então a corrente induzida:
a)
b)
c)
d)
e)
4.
anti-horário, anti-horário e horário.
anti-horário, anti-horário e anti-horário.
horário, horário e anti-horário.
anti-horário, horário e anti-horário.
horário, horário e horário.
A
é nula.
está no sentido horário e é constante no tempo.
está no sentido anti-horário e é constante no tempo.
está no sentido horário e é crescente no tempo.
está no sentido anti-horário e é crescente no tempo.
B
Fig. 9
a
(1R) Ex.: 12) pág. 520, Alberto Gaspar, 1 ed.
(1R) (UEL–PR) Como se explica a geração de eletricidade em uma usina hidrelétrica?
a) A água gira as escovas da turbina e, por atrito, é gerada uma grande concentração de cargas elétricas
de mesmo sinal. A eletricidade estática depois é transportada com a ajuda de transformadores, que
mudam o tipo de eletricidade para o uso doméstico.
b) A força gravitacional da queda de água se transforma na força elétrica, que é transportada por linhas
de transmissão e transformada em energia elétrica nos centros de consumo.
c) O gerador da usina hidrelétrica é composto de eletroímãs e de fios enrolados como em um motor
elétrico. A água, movimentando a turbina, faz girar o conjunto de eletroímãs, variando o fluxo do campo
magnético através dos fios enrolados. A variação do fluxo magnético induz uma força eletromotriz.
d) A água é levemente iônica, e esta propriedade é usada para gerar eletricidade estática, que depois é
transformada no tipo de eletricidade para uso doméstico.
e) A água desce para as turbinas e, por diferença de pressão, produz uma força elétrica nos fios que
compõem o gerador, produzindo a corrente elétrica que é transportada por linhas de alta tensão até os
centros de consumo.
Prof. CristóvãoRMRincoski
REVISÃO: III. Indução Eletromagnética
Material de Apoio de Física VII 16
5.
(1R) – Rafael
(1R) A Figura 7 mostra um circuito e uma espira contidos no plano da folha. O circuito contém uma fonte de
tensão, de fem , e um resistor de resistência R. A resistência deste circuito está sendo diminuída pelo
deslocamento descendente do cursor S.
Fig. 7
Quanto à corrente na espira, assinale a afirmação correta.
a)
b)
c)
d)
R.
e)
6.
A corrente é nula porque não existe contato físico entre os dois circuitos.
Existe uma corrente no sentido horário.
Existe uma corrente no sentido anti-horário.
Aparecerá uma corrente somente quando o cursor parar o seu movimento descendente sobre o resistor
A corrente é nula porque não existe nenhuma fonte de fem nessa espira.
(1R) – Rafael
(1R) (UDESC/2009/Janeiro) Um transformador possui 50 espiras no enrolamento primário e 200 espiras no
secundário.
Ao ligar o primário a uma bateria de tensão contínua e constante de 12 V, o valor da tensão de saída, no
enrolamento secundário, é igual a:
a) 12 V, pois a tensão de saída é igual à tensão de entrada.
b) zero, pois o número de espiras do enrolamento secundário é maior do que o dobro do número de
espiras do primário.
c) zero, pois não há força eletromotriz induzida nas espiras do secundário.
d) 72 V, pois a razão entre a tensão de saída e a tensão de entrada é igual à razão entre o número de
espiras do enrolamento secundário e o número de espiras do enrolamento primário.
e) 48 V, pois a razão entre a tensão de entrada e a tensão de saída é igual à razão entre o número de
espiras do enrolamento primário e o número de espiras do enrolamento secundário.
7.
(1R) – Rafael
(1R) (UDESC/2010/Julho) Na Figura 8 abaixo está representada uma espira
quadrada de lado igual a 10,0 cm, situada no interior de um campo magnético
uniforme B, perpendicular ao plano do papel e dirigido para dentro do papel, cuja
2
intensidade é 0,50 Weber/m . O plano formado pela espira é paralelo ao papel.
Quando o campo magnético tem seu sentido completamente invertido, surge na
espira uma força eletromotriz induzida de 5,0 V.
O intervalo de tempo médio utilizado para inverter completamente o sentido do
campo magnético, neste caso, é:
–4
a) 1,0 x 10 s.
–3
b) 1,0 x 10 s.
–3
c) 2,0 x 10 s.
Fig. 8
d) 10 s.
e) zero.
Prof. CristóvãoRMRincoski
I. Introdução às Equações de Maxwell
Material de Apoio de Física VII 17
INTRODUÇÃO À FÍSICA MODERNA E CONTEMPORÂNEA
INTRODUÇÃO
I – INTRODUÇÃO ÀS EQUAÇÕES DE MAXWELL
FORMULÁRIO E TABELA
Esta parte possui como formulário a tabela abaixo.
I. INTRODUÇÃO ÀS EQUAÇÕES DE MAXWELL
LEI DE GAUSS DA ELETRICIDADE
S E S cos q
ALGUMAS APLICAÇÕES
E
0
1
q
4 0 r
2
e
E
1
2 0 r
LEI DE GAUSS DO MAGNETISMO
S B S cos 0
L E I DA IND UÇÃ O DE F A RA DA Y
B
B
, N
ou
t
t
B
E cos
t
Bbv e i
Bbv
R
LEI DE AMPÈRE E LEI DE AMPÈREMAXWELL
B cos 0 i ,
e
E
B cos 0 i 0 0
t
B
0 i
2 r
e
B 0 n i , com n
N
VETOR DE POYNTING
S
1
0
E B sen
Prof. CristóvãoRMRincoski
I. Introdução às Equações de Maxwell
Material de Apoio de Física VII 18
LISTA DE EXERCÍCIOS 4 (13R)
Atenção:
Montar uma equipe de 4 ou 5 alunos e faça os exercícios abaixo.
Aluno:
Aluno:
Aluno:
Aluno:
Aluno:
1.
Turma:
Turma:
Turma:
Turma:
Turma:
Data:
Data:
Data:
Data:
Data:
/
/
/
/
/
/
/
/
/
/
a
(2R) Baseado no Ex.: 1E) pág. 316, Halliday, 4 ed.
(2R) (a) Verifique, com todas as passagens, o valor numérico da velocidade da luz usando a equação
c
1
0 0
.
(b) Mostre que esta equação está dimensionalmente correta, isto é, o sistema de unidades em ambos os
lados é o SI.
R.:
2.
a
(2R) Baseado no Ex.: 2E) pág. 316, Halliday, 4 ed.
(2R) (a) Mostre que
0
377
0
(o valor e a unidade), esta grandeza é chamada de “impedância do vácuo”
(NP2)
angular correspondente a 60 Hz é igual a 377 rad/s.
(NP1)
. (b) Mostre que a freqüência
R.:
(NP1)
Uma impedância, na presença de uma corrente alternada, pode ser: passiva (resistores – são inertes para freqüência da
Corrente Alternada (CA)) e ativa (indutores e capacitores – são ativos para a freqüência da CA).
(NP2)
Os geradores de Corrente Alternada (CA) operam em 60 Hz, devido à este “casamento de impedâncias” (na Europa e no
Paraguai operam em 50Hz).
Prof. CristóvãoRMRincoski
I. Introdução às Equações de Maxwell
Material de Apoio de Física VII 19
3.
a
(2R) Baseado no Exemplo: 34.3E) pág. 291, Serway, 3 ed.
2
(2R) O Sol proporciona cerca de 1.000 W/m de fluxo eletromagnético à superfície da Terra. (a) Calcular a
potência total incidente num telhado de 8 m 20 m. (b) Qual a quantidade de energia solar (em joules) que
incide sobre o telhado, durante 1 h?
R.:
4.
a
(1R) Baseado no Exemplo: 34.3E) pág. 291, Serway, 3 ed.
(1R) O Vetor de Poynting é dado por:
S
1
0
E B sen
onde S é o vetor de Poynting e é o menor ângulo entre E (campo elétrico) e B (campo
magnético). Ele é considerado como sendo a “energia transportada pela onda eletromagnética”. A potência
transportada pela onda eletromagnética, então, pode ser dada em função do vetor de Poynting:
P S A,
onde S é o Vetor de Poynting e A é a área. Calcule o vetor de Poynting para o telhado do exercício
anterior.
R.:
5.
(1R)
(1R) Se formos analisar friamente, uma corrente elétrica não pode circular através de um capacitor, pois
este apresenta duas armaduras ou placas condutoras separadas por um dielétrico (material isolante). Como
então a corrente elétrica pode fluir através de um capacitor? A resposta não é imediata, mas está inclusa
nas Equações de Maxwell. Se analisarmos o lado direito da Equação VI:
0 i 0 0
veremos que 0
E
t
E
t
tem que representar uma corrente elétrica ou pelo menos ter unidade de corrente
elétrica. Então, este termo é chamado de corrente de deslocamento elétrico, devido a isto, temos dois
tipos de correntes: a corrente de condução (conduz cargas elétricas) i e a corrente de deslocamento
elétrico
id 0
E
.
t
Com base nisto, podemos dizer que entra uma corrente de condução no capacitor, ela se transforma em
corrente de deslocamento dentro do capacitor (dielétrico) e sai corrente de condução do outro lado.
Prof. CristóvãoRMRincoski
I. Introdução às Equações de Maxwell
Material de Apoio de Física VII 20
2
Para um capacitor de placas paralelas de área de 10 cm sendo carregado por uma pequena corrente
condução de 0,885 mA, qual é o campo elétrico, quando o fluxo é máximo, entre as placas do capacitor,
para um tempo de carga de 1 ns.
R.:
6.
(3R)
(3R) Sabendo que uma bobina retangular de lados 5 cm e 10 cm,
como mostram a Fig. 1, está imersa em um campo magnético
uniforme de 0,25 T, ela está sendo puxada com uma velocidade de
2 m/s. (a) Qual é o sentido da fem induzida e da corrente induzida?
(b) Qual é a força eletromotriz induzida, na bobina? (c) Se a sua
resistência interna for de 2,5 , qual deve ser a corrente induzida na
bobina?
R.:
B
5 cm
10cm
v
Fig. 1
7.
a
(2R) Baseado no Ex.: 13P) pág. 317, Halliday, 4 ed.
(2R) Um capacitor de placas paralelas quadradas, de 1,0 m de
lado, como o da Fig. 2, está sendo carregado por uma corrente
de 2,0 A, que chega a uma das placas e sai da outra. (a) Qual é
a corrente de deslocamento na região entre as placas? (b) Se
admitirmos que:
i
J
S
i
e Jd d ,
S
como sendo a densidade de corrente de condução elétrica e
densidade
de
corrente de
deslocamento
elétrico,
respectivamente e S a área. Qual a densidade de corrente no fio
de 2,1 mm de diâmetro (ver Fig. 2) e entre as placas do capacitor?
i
= 2,1 mm
1,0 m
i
Vista de cima
Vista lateral
Fig. 2
R.:
Prof. CristóvãoRMRincoski
I. Introdução às Equações de Maxwell
Material de Apoio de Física VII 21
LISTA DE EXERCÍCIOS 4: EXERCÍCIOS COMPLEMENTARES
1.
2.
a
(4R) – Baseado no Ex.: 42) pág. 973, Halliday, 7 ed., Vol. único.
(4R) Um anel de r = 2,00 cm de raio está carregado, uniformemente,
com q = 6,00 C, gira com uma velocidade angular de
= 4,00 rad/s, em torno do seu eixo central, conforme a Fig. 1. (a)
Qual a frequência de rotação? (b) Qual é o período de rotação? (c)
Esta carga q, levando o período do item (b) quanto representa de
corrente elétrica quando o anel dá uma volta completa? (d) Qual é o
campo magnético no centro do anel?
r
q
Fig. 1
(2R)
4
(2R) Suponha que a luz está se propagando em um meio em que a sua velocidade é de 3 10 m/s. (a)
Quanto deve valer o produto da permissividade elétrica com a permeabilidade magnética, deste meio? (b)
Compare este resultado com o produto 0 0 , para o vácuo, quantas vezes este resultado é maior que o
do item (a)?
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 22
II – INTRODUÇÃO À RELATIVIDADE
FORMULÁRIO E TABELA
Esta parte da revisão possui como formulário a tabela abaixo.
II. INTRODUÇÃO À RELATIVIDADE
TRANSFORMAÇÕES DE GALILEU
ALGUMAS CONSTANTES FÍSICAS
xS x ' v t
yS y '
zS z '
tS t '
vS v ' v
aS a '
REFERENCIAIS NÃO INERCIAIS
x S x ' v0 t A t
aS a ' A
Fin m A
c = 3108 m/s
RT = 6,37 106 m
REFERENCIAIS EM ROTAÇÃO
aco 2 v ' cos
ac 2 r cos 2
g ' g 0 ac aco
EXPERIÊNCIA DE MICHELSONMORLEY
2 Ly
2 Lx
tx
e ty
2
v
v2
c1 2
c 1 2
c
c
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 23
LISTA DE EXERCÍCIOS 5 (13R)
Atenção:
Aluno:
Aluno:
Aluno:
Aluno:
Aluno:
1.
Montar uma equipe de 4 ou 5 alunos e faça os exercícios abaixo.
Turma:
Turma:
Turma:
Turma:
Turma:
Data:
Data:
Data:
Data:
Data:
/
/
/
/
/
/
/
/
/
/
(3R)
(3R) Dois carros transitam com velocidades constantes de 60 km/h e 50 km/h, respectivamente, em
relação a um referencial fixo ao chão. (a) Sem saber para qual lado estão se movendo calcule a maior
diferença de velocidade relativa entre os carros, e (b) qual a menor diferença de velocidade relativa entre os
carros. (c) Pode existir um referencial onde a velocidade relativa é negativa?
R.:
2.
(3R)
(3R) Considere uma pessoa, com massa de 70 kg, em repouso em relação a um carro que vai de 0 km/h a
100 km/h em 10 s, com aceleração constante. (a) Calcule a força inercial (força fictícia) sofrida pelo
motorista contra o encosto do banco do carro. (b) Isto dá quantos kgf (quilograma força)? (c) Qual é o valor
da força inercial quando o carro adota velocidade constante?
R.:
3.
(2R)
(2R) (a) Qual é o valor da velocidade angular da Terra (supondo que o tempo de uma volta completa como
sendo exatamente 24h). (b) Um corpo que cai com velocidade de 5 m/s qual será a Aceleração de Coriolis
máxima sofrida pelo corpo.
R.:
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 24
4.
(1R)
(1R) Se o corpo do item anterior possuir uma massa de 10 kg, qual deve ser o seu peso corrigido pela
2
aceleração de Coriolis? (Dica: supor g0 = 9,8 m/s )
R.:
5.
(1R)
(1R) Um corpo possui massa 50 kg no referencial que está em repouso. Qual será a sua massa em um
referencial que está em movimento com velocidade constante de 10 m/s?
R.:
6.
(1R)
0
(1R) Suponha uma latitude de 30 medida a partir do equador. Qual seria a correção na aceleração da
2
gravidade (9,8 m/s ), usando somente aceleração centrípeta, que deveríamos fazer para um corpo situado
muito próximo à superfície da Terra? (Dica: ver cálculo da velocidade angular da Terra do item 3)
R.:
7.
(2R)
(2R) Suponha que a Experiência de MichelsonMorley tivesse sido realizada, e tivesse obtido sucesso, isto
é, conseguido medir a velocidade da Terra através do éter luminífero. Para isto eles deveriam poder obter o
padrão de interferência da luz. Suponha que seja a diferença de fase entre os raios luminosos que
viajam em x e em y (ver figura do interferômetro Aula 11, pág. 76). A onda luminosa possui freqüência f:
2 t f , como v f
e
v c para a luz, então 2 t
c
.
Suponha que estivéssemos usando um laser de He-Ne (o laser de hélio-neônio: opera com luz vermelha de
3
632,8 nm) para fazer a interferometria, a velocidade da Terra em relação ao éter v = 3 10 m/s e
Lx = Ly = 1 m. (a) Calcule a diferença de tempo medida. (b) Calcule a diferença de fase. (Dica: use uma
planilha para calcular como Excel ou a do Linux e aumente o número de casas depois da vírgula até
aparecer o resultado, a calculadora não consegue calcular).
R.:
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 25
LISTA DE EXERCÍCIOS 5: EXERCÍCIOS COMPLEMENTARES
1)
(1R)
(1R) Suponha que um corpo cai com velocidade de 15 m/s, próximo à superfície da Terra, em uma latitude
0
de 30 , medida a partir do equador. Qual seria o valor da aceleração da gravidade se a Terra parasse de
girar? (Dica: admitir que a aceleração da gravidade medida, quando a Terra está girando, é de
2
g ’ = 9,8 m/s )
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 26
FORMULÁRIO E TABELA
Esta parte da revisão possui como formulário a tabela abaixo.
II. INTRODUÇÃO À RELATIVIDADE
TRANSFORMAÇÕES DE LORENTZ (S’ e S)
x'vt '
x v tS
xS
x ' S
2
2
1 v2 c2
1 v c
yS y '
zS z '
y ' yS
z ' zS
t '
t S v xS c 2
v '
tS
1 v 2 c 2
vS v
1 v vS c
ALGUMAS CONSTANTES FÍSICAS
t ' v x ' c2
vS
2
1 v 2 c 2
v' v
1 v v ' c 2
DILATAÇÃO DO TEMPO (S’ e S)
t
t ' S ou t S t '
1
1 v 2 c 2
CONTRAÇÃO DE FITZGERALDLORENTZ (S’ e S)
L '
L ' LS ou L S
1
1 v 2 c 2
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 27
LISTA DE EXERCÍCIOS 6 (14R)
Atenção:
Montar uma equipe de 4 ou 5 alunos e faça os exercícios abaixo.
Aluno:
Aluno:
Aluno:
Aluno:
Aluno:
1.
Turma:
Turma:
Turma:
Turma:
Turma:
Data:
Data:
Data:
Data:
Data:
/
/
/
/
/
/
/
/
/
/
(1R)
(1R) Tomando como base a contração do comprimento de FitzGeraldLorentz, suponha que no referencial
em repouso (S) seja efetuada uma medida de 1 m. Qual seria a medida deste comprimento no referencial
em movimento (S’) se a sua velocidade fosse v 0,3 c ?
R.:
2.
(1R)
(1R) Se usamos a dilatação do tempo para comparar 1 h no referencial em movimento (S’) , movendo-se
com a mesma velocidade relativa do exercício anterior, em relação ao referencial em repouso relativo (S).
Que valor vamos obter?
R.:
3.
(3R)
(3R) Um observador mede três velocidades relativas observadas (em relação ao referencial onde ele se
encontra). Para outro observador em repouso relativo ao anterior, para quais velocidades devemos usar
Transformações de Galileu e para quais devemos usar as Transformações de Lorentz (calcule o valor de v
em km/h para ter uma “noção da velocidade”):
VELOCIDADE v
v 10
8
3
c
v 10 c
v 0,9 c
4.
VALOR DE v (km/h)
TRANSFORMAÇÃO DE GALILEU
(
)Sim (
)Não
TRANSFORMAÇÃO DE LORENTZ
(
)Sim (
)Não
(
)Sim
(
)Não
(
)Sim
(
)Não
(
)Sim
(
)Não
(
)Sim
(
)Não
(3R)
(3R) O fator gama, ou de Lorentz, é usado para indicar que quando se torna maior que um, significa que
estamos usando velocidades relativísticas (Relatividade Restrita de Einstein). Para um 0,99 , (a) qual
deveria ser a velocidade do referencial S’ em relação ao referencial S. (b) Expresse esta velocidade em
termos de c? (c) Quanto valeria em km/h? (Dica: usar i 1 , indicando um número complexo)
R.:
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 28
5.
(2R)
“Alpha Centauri (α Centauri / α Cen); também conhecida como Rigel Centaurus, Rigil
Kentaurus, Rigil Kent, ou Toliman é a estrela mais brilhante da constelação de Centauro,
sendo a terceira mais brilhante do céu.”
“Esta estrela é, na verdade, um sistema triplo, no qual Alpha Centauri A e Alpha Centauri B
giram em torno de um centro comum, gastando quase 80 anos para completar uma órbita, já
Alpha Centauri C, também chamada de Proxima Centauri gasta mais de 1.000.000 anos para
completar uma órbita em torno das componentes principais e é a estrela mais próxima do Sol, a
4,2 anos-luz, enquanto o sistema Alpha Centauri AB estão um pouco mais distantes a 4,4 anosluz.” (http://pt.wikipedia.org/wiki/Alfa_Centauri)
(2R) Suponha que este sistema triplo de estrelas seja simplesmente chamado de AlfaCentauro, e vamos
considerar que está a 4,3 anos luz (média entre 4,2 e 4,4 anos luz) do nosso Sol. Como todos devem
saber, esta distância significa que se viajarmos a velocidade da luz, nós levaríamos 4,3 anos para chegar
nesta estrela. (a) Qual seria esta distância em km? Represente esta distância em potências de base 10
(ou notação científica). (b) Suponha que desejássemos viajar para esta estrela. Vamos considerar que esta
velocidade c seria impossível de ser atingida para os seres humanos (as equações das Transformações de
Lorentz, no sentido do movimento, tendem ao infinito), e que só conseguíssemos atingir v 0,99 c .
Quantos anos, nós levaríamos, para chegar a esta estrela?
R.:
6.
(2R)
(2R) (a) A Terra gira em torno do Sol com uma velocidade média de aproximadamente de 107.000 km/h.
Esta velocidade pode ser considerada uma velocidade relativística? (b) O Sol gira em torno do centro de
nossa galáxia (Via Láctea) com velocidade média de aproximadamente 900.000 km/h. Esta velocidade
pode ser considerada uma velocidade relativística?
R.:
7.
(2R)
(2R) A Via Láctea se move em relação à galáxia de Andrômeda com uma velocidade de aproximadamente
1.080.000 km/h. (a) Esta velocidade é relativística? (b) Independentemente da resposta anterior, vamos
considerar que esta velocidade é relativística, então quem veria a contração do comprimento e a dilatação
do tempo, os habitantes da Via Láctea ou os de Andrômeda?
R.:
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 29
FORMULÁRIO E TABELA
Esta parte da revisão possui como formulário a tabela abaixo.
II. INTRODUÇÃO À RELATIVIDADE
MOMENTO E ENERGIA RELATIVÍSTICOS
m '
p'm'u
1 v 2 c 2
e
p S m0 u
E p c m 02 c 4
2
ALGUMAS CONSTANTES FÍSICAS
m0
2 2
ENERGIA DE REPOUSO
E m0 c 2
PARTÍCULA DE MASSA m 0 kg
h
E pc e p
ENERGIA CINÉTICA
m0
E c m ' c 2 m0 c 2
c 2 m0 c 2
1 v 2 c 2
1 Å = 10
-10
m
G = 6,67 10 N m /kg
30
MSol = 1,99 10 kg
-11
2
2
h = 6,63 10-34 J s
mp = 1,0073u
mn = 1,0087u
mD = 2,0141u
1u = 1,6605 10
-27
kg
ENERGIA TOTAL
m0
E m ' c2
c2
1 v 2 c 2
RAIO GRAVITACIONAL OU DE SCHWARZSCHILD
2G M
rS
c2
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 30
LISTA DE EXERCÍCIOS 7 (12R)
Atenção:
Aluno:
Aluno:
Aluno:
Aluno:
Aluno:
8.
Montar uma equipe de 4 ou 5 alunos e faça os exercícios abaixo.
Turma:
Turma:
Turma:
Turma:
Turma:
Data:
Data:
Data:
Data:
Data:
/
/
/
/
/
/
/
/
/
/
(2R)
(2R) Através da interpretação de Einstein do Efeito Fotoelétrico é que surgiu a idéia do fóton, como sendo
um pacote (“quantum”) de luz. (a) Calcule o momento linear de um fóton de raios X, cujo comprimento de
-10
onda é 1 Å (10 m), (b) calcule a energia deste fóton.
R.:
9.
(3R)
(3R) A reação de formação do Deutério (ou dêuteron, isótopo do Hidrogênio, que possui um núcleo formado
por um próton mais um nêutron) representado aqui, pela letra D, produz raios gama (fótons), representado
aqui pela letra grega , veja reação indicada a seguir:
p n D .
Onde: a massa do próton é mp 1,0073u (u, aqui, significa unidade de massa atômica), a massa do nêutron
-27
é mn 1,0087u, a massa do Deutério é mD 2,0141u e 1u = 1,6605 10 kg.
(a) Qual a diferença de massa de antes da reação para depois da reação? (b) Nesta reação, houve perda de
massa, ganho de massa, ou a massa permaneceu constante? (c) Qual foi a conversão de massa em
energia? (Dica: estas partículas estão em repouso).
R.:
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 31
10. (2R)
(2R) (a) Qual o fator gama, ou fator de Lorentz, para um elétron com energia cinética de 150 MeV? (b)
Alguns livros usam:
v
,
c
chamado de parâmetro de velocidade . Calcule o parâmetro de velocidade para o fator de Lorentz
calculado no item (a).
R.:
11. (1R)
(1R) Qual é a velocidade de um elétron para que a sua energia cinética relativística seja o triplo da sua
energia de repouso?
R.:
a
12. (1R) Baseado no Ex.: 25E) pág. 143, Halliday, Vol. IV, 4 ed.
(1R) Uma partícula move-se ao longo do eixo x’ de um referencial S’ com a velocidade de 0,40c. O
referencial S’ move-se em relação ao referencial S com velocidade 0,60c. Qual é a velocidade da
partícula medida em S?
R.:
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 32
a
13. (1R) Baseado no Ex.: 56P) pág. 145, Halliday, Vol. IV, 4 ed.
(1R) Qual é a quantidade de energia liberada na explosão de uma bomba nuclear (bomba de fissão),
contendo 3,0 g de material “explosivo” ou fissionável. (Suponha que apenas 10% desta massa venham a
ser convertida em energia liberada).
R.:
14. (2R)
(2R) Considere que João está em um referencial em repouso S e possui uma massa de 70 kg. Maria está
em um referencial S’, que se move com velocidade constante em relação a S, e possui 55 kg. (a) Qual
deve ser a velocidade de Maria para que João determine uma massa de 58 kg para Maria? (b) Devido à
simetria entre referenciais inerciais, considere que Maria vê João se afastando com velocidade
v = 2,5 107 m/s. Qual deve ser a massa de João medida no referencial de Maria?
R.:
15. (2R)
(2R) Raio de Schwarzschild ou Raio Gravitacional. (a) A estrela Antares ( Scorpii ou Alfa Scorpii) é uma
a
estrela supergigante vermelha, na constelação de Scorpius (Escorpião). É a 16 estrela mais brilhante no
céu noturno. Ela possui 15,5 M (este é o símbolo de massa solar, isto é, a massa de Antares é 15,5 vezes
a massa do nosso Sol). Se Antares fosse se tornar um buraco negro, qual seria o raio de Schwarzschild?
(b) Um buraco negro, já formado, passou por um raio gravitacional dado por r S 50 km. Qual
deve ser a massa deste corpo celeste que se tornou buraco negro?
R.:
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 33
EXERCÍCIOS COMPLEMENTARES
FORMULÁRIOS E TABELAS
Os formulários e as tabelas de constantes foram vistas nas páginas 15, 18 e 21.
1.
(2R)
(2R) (a) Se, na experiência de Michelson-Morley, nós pudéssemos ter determinado o padrão de
-4
interferência, onde a diferença de fase fosse de = 10 rad, que é dado como
2 t f .
Suponha que estivéssemos usando um laser de He-Ne (o laser de hélio-neônio: opera com luz vermelha de
632,8 nm), determine o atraso no tempo t. (b) De acordo com os trabalhos de Michelson e Morley, eles
acreditavam que seriam capazes de medir com a precisão de 0,02 rad. Refaça as contas e verifique
como afetaria t.
2.
(2R)
(2R) Um trem bala está andando com uma velocidade de 500 km/h. Um garoto no seu interior liga uma
lanterna e ilumina uma parede que está diretamente na sua frente, no sentido do movimento do trem, a 2 m.
Depois ilumina uma parede lateral do trem que também está a 2 m. (a) Qual é o tempo que a luz leva para
atingir ambas as paredes, sob o ponto de vista clássico (de acordo com a Experiência de Michelson-Morley,
ou Relatividade de Galileu) (b) e sob o ponto de vista moderno (Relatividade de Einstein).
3.
(1R)
(1R) Que velocidade o trem, de Maria, deveria possuir para que ela medisse metade de um comprimento
que João, em repouso, mede?
4.
(1R)
(1R) Um carro viaja a 80 km/h, qual deveria ser a velocidade da luz para que o carro, com esta velocidade,
meça um comprimento que é a 10% (dez por cento) do que é medido em repouso?
5.
(2R)
4
(2R) Suponha que a luz está se propagando em um meio em que a sua velocidade é de 3 10 m/s. (a)
Quanto deve valer o produto da permissividade elétrica com a permeabilidade magnética, deste meio? (b)
Compare este resultado com o produto 0 0 , para o vácuo?
(1R)
(1R) Considere as afirmações a seguir:
6.
I
O movimento dos ventos, que compõe os tornados no hemisfério norte, forma um redemoinho no
sentido anti-horário. Se houvessem tornados (como os do hemisfério norte), no hemisfério sul, estes
formariam redemoinhos no sentido horário.
II Um corpo em queda livre não pode sofrer a ação da Aceleração de Coriolis, pois a queda livre significa
que ele está livre da ação de agentes externos à sua queda. Portanto todo corpo caindo na linha vertical,
continua nesta queda sem sofrer desvios.
III Um objeto em movimento, com Aceleração Centrípeta, é um objeto que está em um Referencial Não
Inercial, logo para aplicarmos as Leis de Newton, devemos tomar cuidado, pois estas foram pensadas para
Referenciais Inerciais.
IV Um carro de corrida movendo-se com velocidade constante em um circuito oval (como o da Fórmula
Indy) não sofre a ação de nenhuma força ou aceleração, logo o seu referencial é tido como sendo um
Referencial Inercial.
a)
b)
c)
d)
e)
7.
Somente as afirmações I e II estão corretas.
Somente as afirmações II e III estão corretas.
Somente as afirmações III e IV estão corretas.
Somente as afirmações I e III estão corretas.
Somente as afirmações II, III e IV estão corretas.
(1R)
(1R) De acordo com a Relatividade de Galileu:
“para um observador em um dado referencial inercial, é impossível para este
distinguir o seu estado de repouso ou de MRU.”
Formule um exemplo que explique esta afirmação.
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 34
8.
(1R) Marcus
(1R) Um certo quasar se afasta da Terra com a velocidade v = 0,87c. Um jato de material é ejetado do
quasar, na direção da Terra, com a velocidade de 0,55c em relação ao quasar. Achar a velocidade do
material ejetado em relação a Terra.
9.
(1R) Marcus
(1R) Dois jatos de material são ejetados, em direções opostas, do centro de uma radiogaláxia. Os dois jatos
se movem a 0,75c em relação a galáxia. Determinar a velocidade de um jato em relação ao outro.
10. (1R) Marcus
(1R) Qual deve ser a velocidade de um relógio ao deslocar-se de modo que marque o tempo a uma taxa
igual à metade da taxa de marcação do tempo de um relógio estacionário?
11. (1R) Marcus
-31
(1R) Um elétron, cuja massa é de 9,11 × 10
kg, move-se com a velocidade 0,750c. Achar o seu momento
relativístico e comparar o resultado com o momento calculado pela expressão clássica. Onde v = 0,750c.
12. (2R) Marcus
(2R) Um elétron se move com a velocidade v = 0,850c. Achar a sua energia total e a sua energia cinética,
em eV. Sabendo que a energia de repouso do elétron é 0,511 MeV.
13. (4R) Marcus
(4R) A energia total de um próton é igual a três vezes a sua energia de repouso. (a) Achar a energia de
repouso do próton em MeV (b) Com que velocidade o próton está se movendo? (c) Determinar a energia
cinética do próton em eV. (d) Qual o momento do próton?
14. (4R) Ramissés
(4R) Uma ambulância se desloca por uma estrada retilínea e ultrapassa um carro que se movimenta no
mesmo sentido com velocidade de 80km/h. Um dos passageiros do carro usa o fenômeno do efeito Doppler
para medir a velocidade da ambulância em relação ao carro e verifica que esta se afasta com velocidade de
90 km/h. (a) Qual é a velocidade da ambulância em relação ao referencial fixo na estrada? (Considere que o
momento em que a ambulância ultrapassa o carro seja um instante inicial t0 e que nesse instante ambos
estavam na mesma posição x0 em relação ao referencial do solo.) Após 6 minutos da ultrapassagem: (b)
Qual é a posição xSf da ambulância em relação ao referencial solo? (c) Qual a posição xf’ da ambulância
em relação ao referencial móvel do carro? (d) O que você pode dizer sobre as posições yS, y ’, zS e z ’ da
ambulância neste momento?
15. (2R) Ramissés
(2R) Após 20 s da decolagem, um foguete que voa verticalmente e possui uma aceleração uniforme
alcança 6 km de altura. (a) Qual o peso de um astronauta que possui massa de 70 kg nesse momento?
(b) Qual o peso aparente do astronauta que possui massa de 70 kg após o foguete atingir uma velocidade
constante?
16. (4R) Ramissés
(4R) A Terra completa uma órbita em torno do Sol aproximadamente a cada 365 dias. Supondo uma órbita
11
circular e que o raio da órbita é de aproximadamente 1,5 10 m, calcule: (a) A aceleração centrípeta (que
é idêntica à aceleração da gravidade do Sol sobre a Terra) que a Terra possui em direção ao Sol. (b)
7
Sabendo que o diâmetro da Terra é de aproximadamente 1,2 10 m, e que o tempo de revolução da Terra
é de aproximadamente 24 horas, calcule a aceleração centrípeta que uma pessoa sobre a Linha do
Equador sofre. (c) Calcule as respectivas forças inerciais e suas direções, sabendo que a massa da pessoa
é de 50 kg. (d) Calcule a diferença de peso aparente que uma pessoa que está exatamente sobre a Linha
do Equador sente ao meio-dia e à meia-noite. Essa diferença de peso aparente é relevante para a vida
cotidiana?
17. (7R) Ramissés
(7R) Calcular o fator gama de Lorentz
1
1 v
2
c2
para os seguintes casos:(a) Um carro em uma rodovia a 120 km/h. (b) Um avião de caça rompendo a
barreira do som 1.225 km/h. (c) Um satélite em órbita em torno da Terra 28.300 km/h. (d) A Terra em
movimento de translação em torno do Sol 105.000 km/h. (e) Estrela em órbita em órbita próxima ao buraco
negro do centro de nossa galáxia (Via Láctea) 18.000.000 km/h. (f) Velocidade de afastamento da galáxia
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 35
mais distante da Via Láctea 104.040.000 km/h. (g) Um próton se movimentando no interior do LHC (Large
Hadron Collider Grande Colisor de Hádrons) do CERN 1.076.000.000 km/h.
18. (2R) Marcelo
(2R) Sabendo que uma partícula qualquer possui energia cinética relativística como sendo a metade da sua
energia de repouso: a) Para qual velocidade este fenômeno pode ser observado? b) Se a energia cinética
relativística diminuir em relação à de repouso, a velocidade da partícula aumenta ou diminui? Prove sua
resposta.
19. (2R) Marcelo
(2R) Admitindo que a energia de um fóton seja a mesma que a energia de repouso de um elétron: a)
Calcule o comprimento de onda do fóton. b) Calcule o momento linear do fóton.
20. (1R) Marcelo Ex.: 28.8) pág. 1120, Serway 4, 3 Ed.
3
(1R) É medida a velocidade de um elétron como sendo 5,0010 m/s 0,003%. Dentro de quais limites
pode-se determinar a posição desse elétron ao longo da direção de seu vetor velocidade?
a
21. (2R) Marcelo Ex.: 27) pág. 1138, Serway 4, 3 Ed.
(2R) Um elétron e um projétil (massa = 10 g) tem, cada um, uma velocidade de magnitude de 900 km/h
exata com uma aproximação de 0,01%. Dentro de que limites podemos determinar: a) a posição do elétron
ao longo da direção da velocidade? b) A posição do projétil ao longo da direção da velocidade?
a
22. (1R) Elberth – Referência [A]
(1R) O Decaimento de um Múon.
Um múon é uma partícula subatômica que ocorre naturalmente na natureza, que é uma partícula instável e
que se transporta com um tempo de decaimento médio de 2,20 s. (Ele é criado por radiação cósmica em
alta na atmosfera da Terra). O múon possui massa de aproximadamente 310 vezes a massa de um elétron
(pósitron).
Assume-se que um múon é criado a uma altitude de 5,00 km acima da superfície da Terra e viaja para o
solo com uma velocidade de 0,995c. Portanto, há um tempo de atraso entre os dois eventos.
Este tempo seria o suficiente para que o múon chegue ao solo?
23. (3R) Elberth – Referência [A]
(3R) O Coração do Astronauta
Um astronauta, em repouso na Terra, tem uma taxa de batimento cardíaco de 70 batimentos/min. Quando o
astronauta está viajando em uma nave espacial à velocidade 0,90c, qual será a taxa de batimento medida
por (a) um observador também na nave, (b) um observador em repouso na Terra e (c) quanto deve ser o
batimento do astronauta para que o observador em repouso na Terra meça 70 batimentos/min.
24. (2R) Elberth – Referência [B]
(2R) O Explorador Espacial
Um explorador espacial viaja a v = 0,95c para uma estrela distante. Após explorar esta estrela por um curto
espaço de tempo, o explorador retorna com a mesma velocidade e chega em casa após 80 anos (medido no
referencial da casa). (a) Quanto tempo o relógio do explorador afirma que ele demorou? (b) Quanto ele
envelheceu?
25. (1R) Elberth – Referência [B]
(1R) Carlos e Denis são irmãos gêmeos. Carlos é físico e astronauta, sendo assim, ele ficou 20 anos
8
viajando em velocidade v = 210 m/s e quando voltou, seu irmão Denis estava com 60 anos de idade. Qual
a idade real de Carlos?
26. (1R) Elberth – Referência [C]
(1R) Determine a energia, em elétron-volt de um fóton que possui frequência igual a f = 1667 kHz.
27. (1R) Elberth – Referência [C]
(1R) Determine a energia de repouso de um elétron.
28. (1R) Elberth – Referência [C]
(1R) Um elétron e um pósitron (anti-elétron) aniquilam-se com momento oposto e de igual magnitude:
. Colisão produz uma nova partícula denominada
na reação
. Qual é a
massa desta nova partícula?
29. (2R) Elberth
(2R) Um colega empresta sua Ferrari capaz de viajar a 0,85c. A Ferrari mede 5,6 m de altura e 18 m de
comprimento em um referencial estacionário. (a) Qual é o comprimento da Ferrari na sua velocidade
Prof. CristóvãoRMRincoski
II. Introdução à Relatividade
Material de Apoio de Física VII 36
máxima? (b) Ainda na velocidade máxima, qual seria o tempo passado no referencial do seu colega se, para
você, passaram-se 2,0 h?
30. (1R) Baseado no exercício apresentado pelo Elberth
(1R) A transformação de velocidades de Lorentz (de S’ para S) é dada por
v' v
vS
,
1 v v ' c 2
tal que v ’ é a velocidade de um objeto paralelas a v como medido no referencial inercial com velocidade
relativa v e vS é a velocidade de um objeto paralela a v medida pelo referencial em repouso. Mostre que um
fóton à velocidade c possui a mesma velocidade em todos os referenciais inerciais (tanto no S’, v ’ = c,
quanto no S, vS = c).
31. (1R) Elberth
(1R) Uma espaçonave chamada Estrela da Morte viajando a 0,8c ejeta um míssil a 0,95c relativa à ela.
Quão rápido o míssil atingiria um asteroide em repouso?
32. (1R) Elberth
(1R) Um observador na Terra observa uma nave alienígena se aproximando à velocidade 0,6c. Uma nave
defensora tenta tomar a nave alienígena e atinge uma velocidade de 0,9c em relação à nave alienígena.
Qual seria a velocidade da nave defensora observada da Terra?
Prof. CristóvãoRMRincoski
Referências
Material de Apoio de Física VII 37
REFERÊNCIAS
REFERÊNCIAS BIBLIOGRÁFICAS
a
[1]
GASPAR, Alberto; “Física, Série Brasil – Ensino Médio”; 1 Edição; vol. Único, Editora Ática, 2004.
[2]
HALIDAY, David; Resnick, Robert; Walker, Jearl; “Fundamentos de Física – Ótica e Física Moderna”; 4
Edição, Livros Técnicos e Científicos Editora S.A., Rio de Janeiro, RJ.
[3]
HALIDAY, David; Resnick, Robert; Walker, Jearl; “Fundamentals of Physics”; 7 Edição, vol. único, John
Wiley & Sons, Inc..
[4]
Serway, Raymond A; “Física”; 3 ed., Rio de Janeiro, RJ, Livros Técnicos e Científicos Editora S. A.
(LTC), 1990.
a
a
a
REFERÊNCIAS ELETRÔNICAS
[A]
Portland State University. Acesso em 14/03/2016. Disponível em: <http://web.pdx.edu/~bseipel/213spring07-relativity.pdf>.
[B]
Worcester
Polythecnic
Institute.
Acesso
em
14/03/2016.
<http://users.wpi.edu/~physics/ph1130c06/Images/ppset01.PDF>.
[C]
University of Florida, Department of Physics. Acesso em
<http://www.phys.ufl.edu/~acosta/phy2061/lectures/Relativity4.pdf>.
Disponível
08/04/2016.
Disponível
em:
em:
Prof. CristóvãoRMRincoski












