v - ELITE CAMPINAS

(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
FÍSICA
Sabe-se que a velocidade do vento é 75% da velocidade do avião.
QUESTÃO 1
intervalos de tempo nas situações (1) e (2), vale
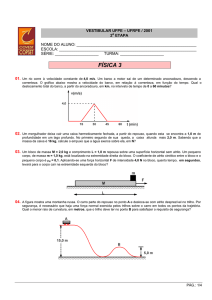
Uma partícula move-se com velocidade de 50 m/s. Sob a ação de uma
aceleração de módulo 0,2 m/s2, ela chega a atingir a mesma
velocidade em sentido contrário. O tempo gasto, em segundos, para
ocorrer essa mudança no sentido da velocidade é
a) 250
b) 500
c) 100
d) 50
Resolução
a)
1
3
b)
AVIÃO
atingir uma velocidade de mesmo módulo, porém em sentido contrário
( v = −50 m / s ), ela deve sofrer uma aceleração no sentido contrário
VENTO
ao seu sentido inicial de movimento, ou seja, a = −0,2 m / s 2 . Sendo
o movimento uniformemente variado, temos:
v = v 0 + at ⇒ −50 = 50 − 0,2 ⋅ t ⇒ t = 500 s
QUESTÃO 2
v 
d)  
g
v2
c)
g
Resolução
AVIÃO
3G
vA
4
2
Alternativa C
d)
5
7
Alternativa D
G
vA
TOTAL
3G
vA
4
G 7G
v1 = v A
4
G
vA
G
vA
3G
vA
4
VENTO
G
v2
TOTAL
Pelo teorema de Pitágoras, temos:
Orientando a trajetória para baixo, e colocando a origem no ponto de
onde o primeiro corpo é abandonado, temos:
G
G
G
3G
5 G
| v 2 |2 =| v A |2 + | v A |2 ⇒| v 2 |= | v A | .
4
4
0
Para uma mesma distância D percorrida nas duas situações:
Corpo 1
v
7
9
Situação (2):
Um corpo é abandonado do repouso de uma altura h acima do solo.
No mesmo instante, um outro é lançado para cima, a partir do solo,
segundo a mesma vertical, com velocidade v. Sabendo que os corpos
se encontram na metade da altura da descida do primeiro, pode-se
afirmar que h vale:
1
2
c)
Resolução
Alternativa B
v 
b)  
g
3
5
Situação (1):
A partícula inicialmente está com velocidade v 0 = 50 m / s . Para
v
a)
g
∆t1
, entre os
∆t2
Para uma mesma distância percorrida, a razão
D
 G
| v1 |= ∆t
G
G

1
⇒| v1 | ∆t1 =| v 2 | ∆t 2 ⇒

G
D
| v |=
 2 ∆t 2
7 G
5 G
∆t
5
| v A | ∆t1 = | v A | ∆t2 ⇒ 1 =
∆t 2 7
4
4
h
Corpo 2
QUESTÃO 4
As equações horárias do movimento de cada um deles são dadas por:
g 2

 y1 = 0 + 0t + 2 t
.

 y = h − vt + g t 2
 2
2
h
Como eles se encontram no ponto y = , da equação horária do
2
corpo 1 vem que:
h g 2
h
= t ⇒t =
g
2 2
Um corpo de massa m, preso à extremidade de um fio, constituindo
um pêndulo cônico, gira num círculo horizontal de raio R, como mostra
a figura.
Substituindo na equação do corpo 2, que nesse instante também
h
chegou ao ponto y = , temos:
2
Sendo g a aceleração da gravidade local e θ o ângulo do fio com a
vertical, a velocidade do corpo pode ser calculada por
2
v2
h
h g h
h
h
= h −v ⋅
+ 
⇒ h2 = v 2 ⋅ ⇒ h = ±
 ⇒h =v


g
2
g 2 g 
g
g
A raiz negativa não convém, devido às hipóteses adotadas (h positivo)
QUESTÃO 3
Considere um pequeno avião voando em trajetória retilínea com
velocidade constante nas situações a seguir.
(1) A favor do vento.
(2) Perpendicularmente ao vento.
1
a)
Rgtgθ
b)
2Rg
c)
Rgsenθ
d)
Rg
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
Resolução
Alternativa A
QUESTÃO 6
As forças que atuam no corpo são o seu peso e a tração do fio. A
resultante dessas duas forças é a força centrípeta:
G
T
Na questão anterior, considere que a bola da situação 2 atinge o solo
com uma velocidade duas vezes maior que a velocidade limite
alcançada pela bola na situação 1. Nestas condições, pode-se afirmar
que o percentual de energia dissipada na situação 1 foi de:
a) 75%
b) 25%
c) 50%
d) 10%
G
T
G
FCP
G
P
Resolução
G
P
Na situação 2, há conservação da energia mecânica, e portanto
podemos escrever:
O polígono de forças correspondente é:
G
P
G
T
θ
Alternativa A
Seja v1 a velocidade limite alcançada na situação 1 e v2 a velocidade
com que a bola atinge o solo na situação 2.
Em ambas as situações, a energia mecânica inicial em relação ao solo
G
é dada pela energia potencial gravitacional, ou seja, E0 = m | g | h .
G
G
mv 2 2
E0 = EC ⇒ m | g | h =
⇒ v2 = 2 | g | h
2
Por outro lado, na situação 1, de acordo com o enunciado:
G
FCP
v1 =
G
1
1
v 2 ⇒ v1 =
2|g |h
2
2
A energia mecânica com que a bola chega ao solo nessa situação é a
Logo, temos:
G
| v |2
G
G 2
m
|F |
RG = | v |G ⇒| vG |= R | gG | tgθ
G =
tgθ = CP
m|g | R|g |
|P |
sua energia cinética
mv12
. Assim, a perda de energia mecânica em
2
relação à energia mecânica inicial será dada por:
2
G 
1
G
mv12
m|g |h−
2
2 2|g |h
v
 =
= 1− 
G 2 = 1−
G1
G
m|g |h
2|g |h
2|g |h
QUESTÃO 5
A figura mostra uma bola de isopor
caindo, a partir do repouso, sob
efeito da resistência do ar, e outra
bola idêntica, abandonada no vácuo
no instante t1 em que a primeira
atinge a velocidade limite.
A opção que pode representar
= 1−
1 3
= = 75%
4 4
QUESTÃO 7
A figura abaixo representa dois corpos idênticos girando
horizontalmente em MCU com velocidades lineares v1 e v2. A razão
T1
entre as intensidades das trações nos fios ideais 1 e 2 é
T2
os gráficos da altura h em função do tempo t para as situações
descritas é:
c)
a)
d)
b)
Resolução
v12 + v 2 2
v 22
b)
2v12 + v 22
v 22
c)
v12 − v 2 2
v 22
d)
v 22
v12
Alternativa C
Observe que foi adotada a orientação positiva para cima.
O movimento da bola na situação 1 será acelerado para baixo
(embora não necessariamente com aceleração constante) até o
instante t1, em que ela atinge sua velocidade limite, e a partir daí
passa a cair em movimento retilíneo e uniforme. Antes de t1, seu
movimento não é uniforme e o gráfico do espaço em função do tempo
não será uma reta, o que descarta as alternativas (b) e (d).
Além disso, antes de t1 a aceleração escalar, apontando para baixo,
será negativa, pois está no sentido contrário àquele adotado como
positivo. Portanto, a curva deve ter concavidade negativa, o que
acontece apenas na alternativa (c).
Finalmente, na situação 2, a bola está em queda livre, e sua equação
horária dos espaços será dada por:
h(t ) = H −
a)
Resolução
Alternativa B
Isolando os corpos 1 e 2, temos:
g (t − t1 )2 , cujo gráfico é uma parábola, também de
2
G
T1
1
G
T2
2
G
T2
Os corpos estão em movimento circular uniforme, portanto a força
resultante sobre cada um deles é de natureza centrípeta:
concavidade negativa, deslocado de t1 para a direita.
2
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
G
G
 G
| v1 |2
|
T
|
−
|
T
|
=
m
 1
2
1
R
 G
G 2
|
|
v
| T |= m
2
2
2
2R

d)
c)
Dividindo membro a membro a primeira equação pela segunda, e
lembrando que as massas m1 e m2 são iguais, já que os corpos são
idênticos, vem que:
G
G
G
G
G
| T1 | − | T2 |
| v1 |2
| T1 |
| v |2
G
= 2 G 2 ⇒ G − 1 = 2 G1 2 ⇒
| v2 |
| v2 |
| T2 |
| T2 |
G
G 2
G 2
| T1 | 2 | v1 | + | v 2 |
G =
G
| v 2 |2
| T2 |
Resolução
QUESTÃO 8
O volume de água necessário para acionar cada turbina de uma
determinada central hidrelétrica é cerca de 700 m3 por segundo,
“guiado” através de um conduto forçado de queda nominal igual a 112
m.
Considere a densidade da água igual a 1kg/L. Se cada turbina
geradora assegura uma potência de 700 MW, a perda de energia
nesse processo de transformação mecânica em elétrica é,
aproximadamente, igual a
a) 5%
b) 15%
c) 10%
d) 20%
Resolução
Alternativa D
Como a pessoa fica em contato apenas com a parede vertical (não há
contato com nenhum tipo de piso), então deve haver alguma força de
atrito exercida pela parede para equilibrar a força peso que atua sobre
a pessoa. Portanto, deverá existir um atrito vertical e dirigido para
cima. A reação normal da parede sobre a pessoa faz o papel de
resultante centrípeta, sendo a responsável pelo movimento circular
uniforme que a pessoa executará junto com o cilindro. Como o
enunciado pediu o diagrama de forças em relação a um referencial fixo
na Terra, que pode ser considerado inercial para a situação do
problema, não existe nenhuma força do tipo centrífuga, uma vez
que forças dessa natureza só aparecem em referencias não-inerciais.
Tal seria o caso se a pergunta sobre o diagrama de forças fosse feita
em relação a um referencial dentro do brinquedo, ou seja, que também
estivesse em movimento de rotação. Além disso, naturalmente, há a
força peso, orientada para baixo, devido ao campo gravitacional da
Terra, que age sobre a pessoa.
QUESTÃO 10
Alternativa C
Em uma apresentação da Esquadrilha da Fumaça, uma das
acrobacias é o “loop”, representado pela trajetória circular da figura.
Ao passar pelo ponto mais baixo da trajetória, a força que o assento
do avião exerce sobre o piloto é
Se não houvesse perdas, a energia gerada seria precisamente a
energia potencial gravitacional da água no topo da queda. Assim:
G
G
E
m⋅ | g | ⋅h ( ρ ⋅ V )⋅ | g | ⋅h
V  G
=
= ρ ⋅   ⋅ | g | ⋅h
P0 = G =
∆t
∆t
∆t
 ∆t 
Onde,
ρ = densidade da água
V = volume de água
Assim, como temos 700 m3 a cada 1 segundo:
P0 = 1,0 ⋅ 10 3 ⋅ 700 ⋅ 10 ⋅ 112 = 784 ⋅ 10 6 W = 784 MW
Como a energia gerada é de fato 700 MW, a perda em relação à
energia potencial gravitacional é dada por:
784 − 700
= 10,7%
784
QUESTÃO 9
a) igual ao peso do piloto.
b) maior que o peso do piloto.
c) menor que o peso do piloto.
d) nula.
A figura representa um brinquedo de
parque de diversão em que as
pessoas, apenas em contato com a
parede vertical, giram juntamente com
uma espécie de cilindro gigante em
movimento de rotação.
Resolução
Alternativa B
Ao passar pelo ponto mais baixo da circunferência descrita, supondo
que o avião esteja em movimento circular e uniforme, temos duas
forças atuando no piloto, ambas verticais: o seu peso, que aponta para
baixo, e a força normal exercida pelo assento do avião, que aponta
para cima.
Considere as forças envolvidas abaixo relacionadas.
JJK
P é a força peso
JJK
Fat é a força de atrito estático
JJJK
Fcp é a força centrípeta
JJK
Fcf é a força centrífuga
G
N
Para um referencial externo, fixo na terra, as forças que atuam sobre
uma pessoa estão representadas pela opção:
b)
a)
G
P
Observe que a soma vetorial dessas duas forças deve ser uma força
resultante de natureza centrípeta, já que o piloto descreve uma
trajetória circular junto com o avião. Como a força centrípeta aponta
sempre para o centro da circunferência descrita, no ponto mais baixo
G
G
da trajetória, a resultante entre N e P deve apontar para cima,
G
G
portanto devemos ter: | N |>| P |
3
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
QUESTÃO 13
QUESTÃO 11
A figura abaixo apresenta dois corpos de massa m suspensos por fios
ideais que passam por roldanas também ideais. Um terceiro corpo,
também de massa m, é suspenso no ponto médio M do fio e baixado
até a posição de equilíbrio.
Três esferas estão suspensas por
fios ideais conforme a figura. Se a
esfera A for deslocada da posição
inicial e solta, ela atingirá uma
velocidade v e colidirá frontalmente
com as outras duas esferas
estacionadas.
M
Considerando o choque entre as esferas perfeitamente elástico, podese afirmar que as velocidades v A , v B e vC de A, B e C , imediatamente
após as colisões, serão:
a) v A = v B = vC = v
b) v A = 0 e v B = vC =
c) v A = v B = 0 e vC = v
d) v A = v B = v C =
Resolução
O afastamento do ponto M em relação à sua posição inicial é:
d 3
d 3
b)
a)
6
3
d 3
d 3
c)
d)
4
2
v
2
v
3
Alternativa
C
Designando as velocidades depois do choque por v’, temos, pela
conservação de energia (choque perfeitamente elástico e=1) no
choque entre A e B:
v
v '- v ' v '- v '
e = afast = B A = B A = 1 ⇒ v B '- v A ' = v (1)
v aprox v A - v B
v -0
Resolução
Pela conservação da quantidade de movimento, temos:
mA .v A + mB .v B = mA .v A '+ mB .v B ' ⇒ m.v + m.0 = m.v A '+ m.v B ' ⇒
Alternativa A
G
T'
G
T
v = v A '+ v B ' (2)
Somando as equações (1) e (2), temos:
2.v B ' = 2.v ⇒ v B ' = v
θ1
G
P
Portanto: v A ' = 0
G
T'
θ3
−T
G
T
Analogamente no choque entre B e C, temos:
v B '' = 0
G
P
G
P
v C '' = v
Logo, imediatamente após as colisões, as velocidades de A e B são
nulas e a velocidade de C é igual a v:
v A = v B = 0 e vC = v
Na figura, temos que as trações têm todas a mesma intensidade (T),
pois os três corpos são idênticos, logo θ1=θ2=θ3=120º. Além disso, da
simetria do problema, podemos concluir que θ3 é dividido pela vertical
em dois ângulos iguais:
QUESTÃO 12
d
A respeito de um satélite artificial estacionário em órbita sobre um
ponto do equador terrestre, afirma-se que:
Ia força que a Terra exerce sobre ele é a resultante
centrípeta necessária para mantê-lo em órbita.
II o seu período de translação é 24 horas.
III os objetos soltos em seu interior ficam flutuando devido à
ausência da gravidade.
Está (ão) correta(s):
a) apenas I.
b) apenas II e III.
c) apenas I e II.
d) I, II e III.
Resolução
G
T
θG2
2
h
60º 60º
G
T
θ1
G
P
Alternativa C
G
T
G
−T
G
T
G
P
G
P
I – Correta: De fato é a força gravitacional que mantém o satélite em
sua órbita. Por ele estar estacionário (geoestacionário), podemos
assumir que sua posição em relação à Terra não se altera e portanto
sua altitude permanece constante (raio constante, num movimento
circular). A força de atração, única força atuante, é perpendicular ao
vetor velocidade e, portanto, é a resultante centrípeta.
II – Correta: Seu período de translação é o mesmo período de rotação
da Terra, para que ele permaneça estacionário em relação à mesma
(sobre uma mesma posição projetada na Terra).
III – Incorreta: Tanto os objetos quanto o satélite estão sujeitos à
mesma ação da gravidade, ou seja, movimentam-se juntos. Daí o fato
dos objetos flutuarem no interior do satélite, eles possuem aceleração
relativa em relação ao satélite nula.
Assim, da figura:
d
tg60º =
2 = d =
h
2h
3 ⇒ h=
d
2 3
=
d 3
6
QUESTÃO 14
Uma viga homogênea é suspensa horizontalmente por dois fios
verticais como mostra a figura abaixo:
4
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
A razão entre as trações nos fios A e B vale:
1
2
5
c)
6
Assim, sabendo que o volume ocupado pela cortiça é maior, E1 < E2 e
2
3
3
d)
4
a)
o
como P1 − E1 = P2 − E2 ⇒ P1 < P2
Re
so
lu
çã
b)
Com isso, no vácuo (onde não existiria empuxo) a balança penderia
para o lado das cortiças.
Alternativa D
Observe a figura:
7L/12
QUESTÃO 16
L/4
TA
Duas esferas A e B de mesmo volume, de
materiais diferentes e presas por fios
ideais, encontram-se em equilíbrio no
interior de um vaso com água conforme a
figura.
Considerando-se
as
forças
peso
( PA e PB ), empuxo ( E A e EB ) e tensão no
TB
L/4
L/6
P
fio ( TA e TB ) relacionadas
a cada esfera, é INCORRETO afirmar que:
b) E A = EB
a) TA < TB
L
A partir do somatório das forças, temos:
(1)
TA + TB = P
A partir do somatório dos momentos em relação ao ponto de
sustentação do fio B, temos:
L
7L
3P
= 0 ⇒ TA =
(2)
P. − TA .
4
12
7
4P
Substituindo (2) em (1) temos: TB =
7
A razão entre as trações será:
3P
TA
7=3
=
TB 4P
4
7
C) TA + TB = PA − PB
Resolução
TA
QUESTÃO 15
TB
PB
Assim, as alternativas b, c e d estão corretas.
Nada podemos afirmar em relação a TA e TB:
PA = TA + E
TA = PA − E
⇒
⇒ TA − TB = ( PA + PB ) − 2E

PB + TB = E
TB = E − PB
Alternativa D
Temos três opções de sistemas que satisfazem as condições do
problema, com densidades possíveis para as esferas:
ρ + ρB
P + PB
⇒E < A
⇒ TA − TB > 0 ⇒ TA > TB
i) Se ρ liq < A
2
2
ρ + ρB
P + PB
⇒E = A
⇒ TA − TB = 0 ⇒ TA = TB
ii) Se ρ liq = A
2
2
ρ + ρB
P + PB
⇒E > A
⇒ TA − TB < 0 ⇒ TA < TB
iii) Se ρ liq > A
2
2
Portanto, não podemos afirmar o que diz a alternativa a.
E1
P2
P1
QUESTÃO 17
P1 = N1 + E1
Assim, como temos o seguinte equilíbrio: 
P2 = N2 + E2
O diagrama de fases apresentado a seguir pertence a uma substância
hipotética. Com relação a essa substância, pode-se afirmar que:
Podemos dizer que: P1 − E1 = P2 − E2
Daí, como o empuxo é dado por: E = ρ . V. g , temos que:
P1 − E1 = P2 − E2 ⇒ ( ρ1 − ρar )V1 = ( ρ2 − ρar )V2 ⇒
EB
PA = TA + E A
A partir da figura temos 
PB + TB = EB
Para esfera de mesmo volume o empuxo é igual E A = EB
Assim:
PA − TA = PB + TB ⇒ PA − PB = TA + TB
Como TA e TB são os módulos das trações (positivos), podemos
concluir que PA > PB
Denotando os índices 1 para ferro e 2 para cortiça, como no ar a
balança está em equilíbrio e considerando a balança com os braços
iguais N1 = N2
N2
E2
N1
Alternativa A
EA
PA
Uma balança está em equilíbrio, no ar, tendo bolinhas de ferro num
prato e rolhas de cortiça no outro. Se esta balança for levada para o
vácuo, pode-se afirmar que ela:
a) penderia para o lado das bolinhas de ferro, pois a densidade do
mesmo é maior que a densidade da cortiça.
b) não penderia para nenhum lado, porque o peso das bolinhas de
ferro é igual ao peso das rolhas de cortiça.
c) não penderia para nenhum lado, porque no vácuo não tem empuxo.
d) penderia para o lado das rolhas de cortiça, pois enquanto estava no
ar o empuxo sobre a cortiça é maior que o empuxo sobre o ferro.
Resolução
d) PA > PB
( ρ1 − ρar ) = V2
( ρ2 − ρar ) V1
Como ρ1 > ρ 2 > ρar ⇒ V1 < V2 (como descrito na figura)
5
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
L
S
V
a) nas condições normais de temperatura e pressão, a referida
substância se encontra no estado sólido.
b) se certa massa de vapor da substância à temperatura de 300º C for
comprimida lentamente, não poderá sofrer condensação, pois está
abaixo da temperatura crítica.
c) se aumentarmos gradativamente a temperatura da substância,
quando ela se encontra a 70º C e sob pressão de 3 atm, ocorrerá
sublimação da mesma.
d) para a temperatura de 0ºC e pressão de 0,5 atm, a substância se
encontra no estado de vapor.
Resolução
d) Verdadeiro. De acordo com o gráfico, o ponto citado está de fato
na região em que a substância se encontra no estado de vapor.
L
S
V
Alternativa D
QUESTÃO 18
A figura a seguir representa o Ciclo de Carnot realizado por um gás
ideal que sofre transformações numa máquina térmica. Considerandose que o trabalho útil fornecido pela máquina, em cada ciclo, é igual a
1500 J e, ainda que, T1 = 600 K e T2 = 300 K, é INCORRETO afirmar
que
a) Falso. Nas condições normais de temperatura e pressão (0 °C e 1,0
atm) a referida substância está no estado de vapor. Observe onde
está o ponto no gráfico:
a) de B até C o gás expande devido ao calor recebido do meio
externo.
b) a quantidade de calor retirada da fonte quente é de 3000 J.
c) de A até B o gás se expande isotermicamente
d) de D até A o gás é comprimido sem trocar calor com o meio
externo.
L
S
V
Resolução
Alternativa A
Como a máquina opera segundo um ciclo de Carnot, seu rendimento é
dado por:
T
300 1
η = 1− 2 = 1−
=
T1
600 2
b) Falso. Ao comprimir lentamente, podemos assumir que se trata de
um processo isotérmico, ou seja, a curva que representa o processo
seria um segmento de reta vertical no gráfico:
Por outro lado, sendo Q1 o calor absorvido da fonte quente e Q2 o
calor rejeitado para a fonte fria, temos também:
τ = Q1 − Q2
1500 = Q1 − Q2
Q = 3000 J


⇒  1 1500
⇒ 1
τ

η
=
=
Q2 = 1500 J

2
Q1
Q1


L
S
V
a) Incorreta: o ciclo de Carnot é formado por duas transformações
isotérmicas (trechos AB e CD) e duas transformações adiabáticas
(trechos BC e DA). Sendo o trecho BC uma transformação adiabática,
não há troca de calor com o meio nessa fase, e o trabalho que o gás
realiza nessa expansão vem de sua energia interna, de acordo com a
Primeira Lei da Termodinâmica.
b) Correta: calculado acima.
c) Correta: a transformação AB é uma expansão (volume em B maior
que volume em A) e se realiza à temperatura constante T1.
d) Correta: a transformação DA é uma compressão (volume em A
menor que volume em D) e como é adiabática, não há troca de calor
com o meio. Nesse caso, a energia recebida do meio sob a forma de
trabalho é armazenada como energia interna do gás.
Assim, se a substância atingir pressões próximas a 4 atm ou
superiores, passará do estado de vapor para o estado líquido, ou seja,
sofrerá condensação.
c) Falso. Quando a substância está a 70 °C e sob pressão de 3 atm,
ela se encontra no estado sólido. Além disso, se submetermos essa
substância a uma expansão isobárica, sua temperatura aumentará até
que sofra fusão e passe para o estado líquido, e não diretamente para
o estado gasoso.
6
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
QUESTÃO 19
O raio de luz que parte de A e atinge o observador O é refletido pelo
espelho no ponto P.
A distância percorrida pelo raio pode ser obtida aplicando o teorema
de Pitágoras:
Um cilindro de volume constante contém determinado gás ideal à
temperatura T0 e pressão p0. Mantém-se constante a temperatura do
cilindro e introduz-se, lentamente, a partir do instante t = 0, certa
massa do mesmo gás.
O gráfico abaixo representa a massa m de gás existente no interior do
cilindro em função do tempo t.
d 2 = 9 2 + (8 + 4)2 ⇒ d = 15 m
QUESTÃO 21
Um espelho esférico E de distância focal f e uma lente convergente L
estão dispostos coaxialmente, com seus eixos ópticos coincidentes.
Uma fonte pontual de grande potência, capaz de emitir luz
exclusivamente para direita, é colocada em P. Os raios luminosos do
ponto acendem um palito de fósforo com a cabeça em Q, conforme
mostra a figura.
Nessas condições, a pressão do gás existente no recipiente, para o
instante t = a, é igual a
a) 2,0 p0
b) 1,5 p0
d) 4,0 p0
c) 2,5 p0
Resolução
Alternativa B
A massa de gás existente no interior do cilindro é dada por:
b
m( t ) =
t +b.
2a
Aplicando a equação de Clapeyron para os instantes t = 0 e t = a,
temos:
m(0)

pV =
RT0
 p0V = n0RT0
 0
M
⇒


 pV = nRT0
 pV = m(a ) RT
0

M
Dividindo as duas equações membro a membro, vem:
Considerando-se as medidas do esquema, pode-se afirmar que a
distância focal da lente vale
2
f
a) f
b)
3
2
f
c)
d) f
3
p0 m(0)
b
3
=
=
⇒ p = p0 = 1,5 p0
2
p m(a ) b + b
2
Resolução
Alternativa A
Os raios de luz que partem de P incidem no espelho E e formam a
primeira imagem exatamente no ponto P. Aplicando a equação de
Gauss para esse espelho, temos:
1 1 1
1 1 1
+
= ⇒ + = ⇒ d = 2f
p p' f
d d f
Essa primeira imagem agora se comportará como objeto para a lente
L, formando a imagem final em Q. Nesse caso, como tanto o objeto
quanto a imagem são reais, aplicando novamente a equação de
Gauss, agora para a lente, vem que:
1
1 1
d 2f
+ = ⇒ fL = =
3 3
 d  d fL
 
2
QUESTÃO 20
A figura mostra um objeto A, colocado a 8 m de um espelho plano, e
um observador O, colocado a 4 m desse mesmo espelho.
8m
A
9m
O
QUESTÃO 22
4m
Considere uma película transparente de faces paralelas com índice de
refração n iluminada por luz monocromática de comprimento de onda
no ar igual a λ , como mostra a figura abaixo.
Um raio de luz que parte de A e atinge o observador O por reflexão no
espelho percorrerá, nesse trajeto de A para O,
a) 10 m
b) 12 m
c) 18 m
d) 15 m
Resolução
Alternativa D
Traçando o ponto A’, simétrico do ponto A em relação ao espelho,
temos o trajeto representado abaixo:
8m
8m
A’
A
Sendo a incidência de luz pouco inclinada, a mínima espessura de
película para que um observador a veja brilhante por luz refletida é
λ
λ
λ
λ
a)
b)
c)
d)
n
2n
5n
4n
9m
P
O
4m
7
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
Resolução
Alternativa D
d)
Para que o observador veja uma intensificação da luz refletida, existe
interferência construtiva da luz que é diretamente refletida (na
superfície) e aquela que é refratada, sofre reflexão na parte inferior da
película e é novamente refratada. Como o índice de refração da
película é maior que o do meio, temos que durante a reflexão na parte
superior da película o feixe sofre inversão de fase, enquanto a reflexão
na parte inferior da película não apresenta esta inversão. A situação
descrita é:
180o de
mudança de
fase
M +m
K
e
mv
M +m
M +m
K
Resolução
Alternativa B
Na colisão da bala com o bloco, ocorre conservação da quantidade de
movimento do sistema:
G
G
mv
QANTES = QDEPOIS ⇒ mv = (M + m )v ' ⇒ v ' =
M +m
A partir desse momento, o sistema passa a descrever um MHS em
torno da posição x = 0 indicada na figura do enunciado. Na posição
em que o sistema atinge sua posição extrema à esquerda ( x = −a ),
sua energia cinética foi toda convertida em energia potencial elástica.
Impondo a conservação de energia mecânica entre essas duas
posições (não existem forças dissipativas), vem que:
sem
mudança
de fase
Ar
Película
2
Ka 2 (M + m )(v ')2
Ka 2 (M + m )  mv 
=
⇒
=

 ⇒
2
2
2
2
M +m
Ar
2
mv
M +m
 mv  (M + m )
a2 = 
⇒a=

K
M +m
K
M +m
Por outro lado, da definição de ω para o MHS:
Para que ocorra uma interferência construtiva, a onda 2 , que vai
percorrer um caminho maior, deve, ao ser refratada pela segunda vez,
estar em fase com a onda 1. Isto ocorrerá se a diferença de caminhos
entre o raio 1 (diretamente refletido) e o raio 2 (refratado, refletido e
refratado) for um número ímpar (devido à inversão de fase de uma das
ondas) de meio-comprimentos de onda no meio da película.
Note que enquanto a luz percorre o caminho 2 dentro da película, ela
mantém sua freqüência, mas diminui sua velocidade. Portanto, altera
seu comprimento de onda. O comprimento de onda no meio da
λ
película é λn = .
n
Assim, como a incidência é pouco inclinada, a diferença de caminhos
(que deve ser igual a um número ímpar de meio-comprimentos de
onda no meio da película) deve ser igual a 2t (onde t é a espessura):
Portanto:
λ 
2 ⋅ t = k ⋅  n  com k = 1, 3, 5...
 2 


A espessura mínima para que ocorra interferência construtiva é para k
λ
= 1, onde temos t =
.
4n
ω2 =
K
K
⇒ω =
M +m
M +m
QUESTÃO 24
Considere um sistema formado por duas cordas diferentes, com
densidades µ1 e µ2 tal que µ1 > µ2, em que se propagam dois pulsos
idênticos,conforme mostra a figura abaixo.
A opção que melhor representa a configuração resultante no sistema
após os pulsos passarem pela junção das cordas é:
QUESTÃO 23
Um projétil de massa m e velocidade v atinge horizontalmente um
bloco de massa M que se encontra acoplado a uma mola de constante
elástica K, como mostra a figura abaixo.
Resolução
Após o impacto, o projétil se aloja no bloco e o sistema massa-molaprojétil passa a oscilar em MHS com amplitude a . Não há atrito entre
o bloco e o plano horizontal nem resistência do ar. Nessas condições,
a posição em função do tempo para o oscilador harmônico simples é
dada pela expressão x = a cos(ω t + ϕ 0 ) , onde a e ω valem,
respectivamente,
(M + m )v
K
e
a)
K
M +m
b)
c)
mv
M +m
e
M +m
K
K
e
M +m
Alternativa B
A situação exposta nas alternativas indica que deseja-se obter a
situação após a refração e reflexão de ambas as ondas. Lembrando
que:
- Na refração do pulso de onda não existe inversão do pulso.
- Não ocorre inversão na reflexão quando o pulso incide da corda de
maior densidade linear para a de menor.
- Ocorre inversão na reflexão quando o pulso incide da corda de
menor densidade linear para a de maior.
Analisando a situação na corda 1 temos que:
i) O pulso que vem da corda 2 não sofre inversão na refração.
ii) O pulso que vem da corda 1 quando refletido também não sofre
inversão.
Logo, na corda 1 deve existir um pulso para cima (refletido) e outro
para baixo (refratado).
K
M +m
M +m
K
8
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
Analisando a situação da corda 2 temos que
i) O pulso que vem da corda 1 não sofre inversão na refração.
ii) O pulso que vem da corda 2 quando refletido sofre inversão.
Logo, na corda 2 deve existir dois pulsos para cima.
A única alternativa que apresenta tal situação é a alternativa B. Vale
ressaltar que a ordem dos pulsos na corda 1 poderia ser diferente,
dependendo da velocidade de propagação de cada onda e da
distância dos pulsos até o ponto de refração.
Resolução
QUESTÃO 25
Alternativa A
O circuito pode ser esquematizado como:
Um corpo B, de massa igual a 4 kg e carga elétrica +6 µC, dista 30
mm do corpo A, fixo e com carga elétrica -1 µC. O corpo B é suspenso
por um fio isolante, de massa desprezível ligado a uma mola presa ao
solo, como mostra a figura. O comprimento natural da mola é L0 = 1,2
m e ao sustentar estaticamente o corpo B ela se distende, atingindo o
comprimento L = 1,6 m. Considerando-se a constante eletrostática do
meio k = 9.109 N.m2/C2, que as cargas originais dos corpos pontuais A
e B são mantidas e desprezando-se os possíveis atritos, o valor da
constante elástica da mola, em N/m, é:
A corrente que circula nesse circuito é:
ε = (R + r ) ⋅ i ⇒ i =
a) 320
b) 200
c) 600
Resolução
G
P = (ε − r ⋅ i ) ⋅ i = ε ⋅ i − r ⋅ i 2
Ou seja, o gráfico da potência em função da corrente é uma parábola
e é dado por:
B
Seja FC a força de Coulomb entre as duas cargas. Como as cargas
G
P
têm sinais opostos, tal força será de atração. Seja também FEL a força
elástica que a mola aplica no corpo B. O diagrama de forças para o
corpo B, já decompondo o peso em suas componentes paralela e
perpendicular ao plano inclinado, está representado a seguir:
G
N
ε2
4r
G
FEL
G
FC
0
G
Px
.
A potência dissipada no resistor R é:
d) 800
Alternativa
ε
R+r
60°
G
Py
ε
ε
2r
r
i
Para que a potência transmitida seja máxima, devemos ter i =
nesse caso, P =
Como o corpo está em repouso:
G
G
| N |=| Py |
G
G
 G
| Px | + | FC |=| FEL |
ε2
4r
ε
2r
e,
, que são as coordenadas do vértice da parábola.
502 625
=
W
4⋅3
3
Q
, quando a potência for máxima, o tempo para o
Como P =
∆t
aquecimento será mínimo. Esse tempo mínimo será:
Q
2 ⋅ 105
∆tMIN =
=
= 960 s = 16 min .
PMAX  625 
 3 


Assim, o tempo de aquecimento do líquido foi de pelo menos 16
minutos, portanto superior a 15 minutos.
Logo, PMAX =
Da última equação:
G
k ⋅ | q A | ⋅ | qB |
= kMOLA ⋅ (L − L0 ) ⇒
m⋅ | g | ⋅ cos 60° +
d2
1 (9 ⋅ 109 ) ⋅ (1⋅ 10 −6 ) ⋅ (6 ⋅ 10−6 )
4 ⋅ 10 ⋅ +
= kMOLA ⋅ (1,6 − 1,2)
2
(30 ⋅ 10−3 )2
20 + 60
kMOLA =
= 200 N / m
0,4
QUESTÃO 26
QUESTÃO 27
Aqueceu-se certa quantidade de um líquido utilizando um gerador de
f.e.m. ε = 50 V e resistência interna r = 3 Ω e um resistor de resistência
R. Se a quantidade de calor fornecida pelo resistor ao líquido foi de
2.105 J, pode-se afirmar que o tempo de aquecimento foi:
a) superior a 15 minutos.
b) entre 6 e 10 minutos.
c) entre 12 e 15 minutos.
d) inferior a 5 minutos.
No circuito representado abaixo, os geradores G1 e G2 são ideais e os
resistores têm a mesma resistência R.
9
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
Assim: U xy = ε − r ⋅ i ⇒ U xy = ε − r ⋅
ε
RAB


r
= ε 1 −

+r
 RAB + r 
No capacitor, temos:


r
Q = CU xy ⇒ Q = C ⋅ ε  1 −

R
r
+


AB
O gráfico desta função de RAB é nulo quando RAB = 0, tende a Q = C.ε,
quando RAB tende a valores muito altos:



r
lim C ⋅ ε  1 −
 = C ⋅ ε
RAB →∞
+
R
r

 
AB

O gráfico que melhor representa tal situação é dado por:
Se a potência dissipada por R2 é nula, então a razão entre as f.e.m. de
G1 e G2 é:
a) ¼
b) 2
c) ½
d) 4
Resolução
Alternativa C
Se a potência dissipada no resistor 2 é zero, então não há corrente
atravessando esse trecho do circuito, de modo que só existe corrente
no ramo da direita
i
i
i
i
Além disso, se não existe corrente circulando no trecho à esquerda,
então não existe queda de tensão nos resistores 1 e 2, portanto
E1 = U3 = R3 ⋅ i .
O gerador G2, por sua vez, alimenta os resistores 3 e 4:
QUESTÃO 29
A figura mostra uma região na qual atua um campo magnético
uniforme de módulo B. Uma partícula de massa m, carregada
positivamente com carga q, é lançada no ponto A com uma velocidade
de módulo v e direção perpendicular às linhas do campo. O tempo que
a partícula levará para atingir o ponto B é
E2 = (R3 + R4 ) ⋅ i
Como todos os resistores têm a mesma resistência R, temos:
E1 = R ⋅ i
E
1
⇒ 1 = .

E2 2
E2 = 2R ⋅ i
QUESTÃO 28
No
circuito
esquematizado
abaixo, C é um capacitor, G um
gerador de f.e.m. ε e resistência
interna r e AB um reostato.
O
gráfico
que
melhor
representa a carga acumulada
Q no capacitor
a)
π Bq
b)
m
2π m
Bq
c)
πm
d)
Bq
Resolução
π Bq
2m
Alternativa C
Como a velocidade é perpendicular ao campo magnético, a força
magnética de Lorentz será uma força resultante de natureza
centrípeta, agindo sobre a carga q.
G
G
G
G
G
| v |2
FM = FCP ⇒| q | ⋅ | v | ⋅ | B | ⋅sen90° = m
⇒
R
em função da resistência R do reostato é:
a)
b)
G
G | q | ⋅ | B | ⋅R
| v |=
m
A carga entrará em movimento circular uniforme dentro da região onde
existe campo magnético, descrevendo uma semicircunferência a partir
do ponto A até abandonar a região no ponto B.
d)
c)
G
v
Resolução
G
FM
Alternativa B
Denominando a resistência no reostato por RAB, e a diferença de
potencial no capacitor por Uxy temos:
B
A
Assim, o tempo que a partícula leva para atingir o ponto B é o tempo
que ela demora para percorrer essa semicircunferência:
G
G ∆s
| q | ⋅ | B | ⋅R π ⋅ R
π ⋅m
| v |=
⇒
=
⇒ ∆t = G
∆t
m
∆t
|B |⋅|q |
A corrente no circuito, no estado estacionário, pode ser calculada por
ε
i=
RAB + r
10
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE O VESTIBULAR DA AFA 2008 FÍSICA
QUESTÃO 30
Uma espira condutora é colocada no mesmo plano e ao lado de um
circuito constituído de uma pilha, de uma lâmpada e de um interruptor.
As alternativas a seguir apresentam situações em que, após o
interruptor ser ligado, o condutor AB gera uma corrente elétrica
induzida na espira, EXCETO:
a) mover a espira na direção y.
b) desligar o interruptor.
c) “queimar” a lâmpada.
d) mover a espira na direção x.
Resolução
Alternativa A
Como o condutor AB está sendo percorrido por uma corrente elétrica,
ele gera um campo magnético na região da espira. Caso este campo
varie (o que pode ser causado por variação de distâncias ou de
correntes), teremos uma variação no fluxo magnético na espira, o que
induz uma corrente na mesma (Lei de Lenz).
Considerando as dimensões do condutor AB muito maiores que as da
espira e a distância da mesma ao condutor pequena, podemos
desconsiderar os efeitos de borda. Também desconsideraremos os
efeitos do restante do circuito.
Assim, ao movermos a espira no eixo y, teremos que a distribuição do
campo sobre a espira permanece a mesma e, portanto, não há
variação de fluxo (ou seja não haverá corrente induzida).
Ao desligarmos o interruptor e ao “queimar” a lâmpada, teremos uma
variação de corrente no condutor, o que diminui o campo na região da
espira e induz corrente (alteração do fluxo).
Ao mover a espira no eixo x, teremos que a distribuição do campo
sobre a espira se altera e, portanto, temos alteração no fluxo e
também aparecimento de corrente induzida.
11