Circuitos especiais

Instrumentação e Técnicas de Medidas
Amplificadores e Circuitos Especiais
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
1
Controle de Versões
2013
Versão 1 – Instrumentação e Técnicas de Medidas (ITM)
Com base nas notas de aula de COB783 e Op Amp Applications Handbook,
Section 4, edited by Walt Jung (Newnes, 2006).
Versção 1.1 – Ordem dos capítulos, equações mais comuns para linearização de
termistor.
Última alteração: 28/08/2013
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
2
Índice
8 Amplificadores de Instrumentação...................................................................................................4
8.1 Amplificador Subtrator.............................................................................................................4
8.2 Amplificador de Instrumentação com Três Operacionais......................................................10
8.3 Amplificador de Instrumentação com Dois Operacionais......................................................11
8.4 Amplificador com Realimentação Ativa................................................................................12
8.5 Amplificador operacional de transcondutância (OTA)..........................................................13
8.6 Amplificador Isolador.............................................................................................................16
8.7 Amplificador chopper.............................................................................................................18
8.8 Amplificador Diferencial Completo.......................................................................................20
8.9 Amplificador de Ganho Programável (PGA).........................................................................21
9 Circuitos Especiais.........................................................................................................................22
9.1 Conversores Tensão Corrente.................................................................................................22
9.1.1 Outras topologias............................................................................................................22
9.2 Potenciômetro Digital.............................................................................................................26
9.3 Conversores AD e DA............................................................................................................26
9.4 Referências de Tensão e Corrente..........................................................................................28
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
3
8 Amplificadores de Instrumentação
8.1 Amplificador Subtrator
Os amplificadores de subtratores são circuitos que amplificam a diferença entre duas
tensões, com uma elevada rejeição a sinais de modo comum e um ganho diferencial ajustável,
funcionando de forma similar ao próprio AO, porém com ganhos menores.
O amplificador subtrator (diferencial) básico é apresentados na Figura 8.1. A configuração
permite alterar o ganho do amplificador mas a impedância de entrada é baixa.
Figura 8.1: Amplificador diferencial básico
Este amplificador pode ser estudado por superposição.
a) para a entrada vcm e v 2
v O =(v CM +v 2 )⋅
R4 R2+R1
⋅
;
R3+R4 R1
b) para a entrada formada por vcm e v 1
v O =−
R2
⋅(v +v ) ;
R1 CM 1
c) somando as duas equações, e após algum algebrismo
[
vO=
]
R1⋅R4 −R2⋅R3
R
R 1+R 2 / R1
⋅v CM − 2⋅v 1 + 4⋅
⋅v .
R1⋅(R3 +R4 )
R1
R3 1+R 4 / R3 2
Se
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
4
R2 R3
=
R1 R 4
então
vO=
R2
⋅(v −v ) .
R1 2 1
Observe que a influência de vcm é nula, se a razão entre as resistências R 2 e R1 for
exatamente igual a razão entre as resistências R3 e R4. Para calcular a CMRR do subtrator em
função da falta de casamento entre as resistências pode-se utilizar a equação 8.1 (Precision Matched
Resistors Automatically Improve Differential Amplifier CMRR – Here’s How, Linear Technology).
()
()
1
⋅(G+1)
2
CMRRR ≈
1 ΔR
⋅
2 R
(8.1)
A Tabela 8.1 mostra como o CMRR do circuito pode mudar com relação a tolerância dos
resistores. Observe que para resistores com tolerância de até 0,1% o CMRR do subtrator é
relativamente pequeno. A solução para este problema é integrar os resistores ou todo o circuito.
Exemplos destes circuitos integrados são o AMP03, o AD628, AD629 da Analog Devices, e os
INA149 e INA146 da Texas Instruments.
Tabela 8.1: CMRR do subtrator em função da tolerância dos resistores
Tolerância dos Resistores (%)
5
2
1
0,1
Acm subtrator (ganho 1)
0,1
0,04
0,02
0,002
CMRRsubtrator (ganho 1)
10x (20dB)
25x (27dB)
50x (33dB)
500x (54dB)
A CMRR do circuito completo, levando em conta a influência da CMRR do amplificador
pode ser obtida por
CMRRR
ONLY
≈
()
()
1
⋅(G +1)
2
()
1
1
1 ΔR
⋅(G+1)+
CMRRamp 2
2 R
(8.2)
Observe que a própria impedância da fonte pode causar um desbalanço nos resistores e
diminuir a CMRR da configuração. Por esta razão é desejável uma topologia onde a impedância de
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
5
entrada seja extremamente elevada. A construção integrada deste amplificador também minimiza os
erros entre as resistências e propicia um CMRR maior.
Exemplo 1: Calcular o CMRR para um amplificador diferencial cujas relações de
resistências são: R2=100·R1, e R4=101·R3.
[
v 0=
v 0=
v 0=
]
R 1⋅R 4−R 2⋅R3
R2
R4 1 R2 / R1
⋅v CM − ⋅v 1  ⋅
⋅v
R1⋅ R3 R 4 
R1
R3 1R 4 / R 3 2
101⋅R1⋅R3 −100⋅R1⋅R3
R1⋅ R3 101⋅R3 
1100
⋅v CM −100⋅v 1101⋅
⋅v
1101 2
1
⋅v −100⋅v 1 100 ,0098⋅v 2
102 CM
CMRR=
Ad 100
=
=10200≈80 dB
ACM 1/102
Exemplo 2: Calcular a função de transferência da topologia abaixo
Considerando que a tensão na saída do amplificador de realimentação é v G , então
v G =−
RK
⋅v
RG O
O problema pode ser resolvido por superposição:
com a entrada v 2 aterrada, a corrente pelos dois resistores da entrada positiva de A1 devem
ser iguais, e v + deve ser zero, então
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
6
v1
v
=− G
R
R
substituindo a equação de v G temos
v1
R
−
=−
RK
⋅v
RG O
R
logo
v O=
RG
RK
⋅v 1
com a entrada v 1 aterrada, o potencial em v – é metade do valor de v 2 , e v + é metade da
tensão v G
v2
2
=
vG
2
−
=
RK
⋅v
RG O
2
então
v O=−
RG
RK
v2
logo
v O=
RG
(v −v )
RK 1 2
O ganho é diretamente proporcional à RG, mas a impedância de entrada fica diminuída.
Exemplo 3: Calcular a função de transferência da topologia abaixo
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
7
Este circuito pode ser redesenhado como
(
(
v 1 =i 3⋅R2=
v 2 =i 4⋅R2=
i=
e1
R1
−
)
v eO
+ −i ⋅R2
R1 R2
)
e2 v
− +i ⋅R2
R1 R1
v 1 −v 2
R
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
8
(
(
)
e2 v
1 e1 v e0
i= ⋅
− + −i− + −i ⋅R 2
R R 1 R1 R2
R 1 R1
i=
R2 e 1 e 2 e 0
⋅
− + −2⋅i
R R1 R1 R 2
(e 1 −e 2 )⋅
i=
)
R2
+e
R1 0
2⋅R2 +R
Reescrevendo novamente as equações


v 1 =v−i 1⋅R 2=v−
v 2 =v−i 2⋅R2 =v−
i=


e1 v
−
⋅R2
R1 R1
e2
R1
−
v
⋅R 2
R1
v 1 −v 2
R
[ 

 ]
e1 v
e2 v
1
i= ⋅ v−
−
⋅R 2 −v
−
⋅R 2
R
R1 R1
R 1 R1
i=
R2
⋅ e −e 
R⋅R1 2 1
igualando as duas correntes i
R2
e
R1 0
R
= 2 ⋅ e 2 −e 1 
2⋅R 2 R
R⋅R 1
 e 1−e 2 ⋅
[
e 0=
e 0=
]
R2
R2
⋅ 2⋅R2 R 
⋅ e 2 −e1 
R⋅R1
R1
 
2⋅R 2 R2
⋅
1 ⋅ e 2−e1 
R1
R
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
9
8.2 Amplificador de Instrumentação com Três Operacionais
O circuito clássico para amplificador de instrumentação, e que resolve todos os problemas
apresentados é apresentado na Figura 8.2.
Figura 8.2: Amplificador de instrumentação com três operacionais.
O circuito pode ser resolvido por superposição.
a) supondo v 2 aterrada, o potencial na entrada negativa do AO de baixo é zero, logo
v O1=v 1⋅
R+R 3
,e
R
v O2=−v 1⋅
R3
;
R
b) supondo v 1 aterrada, o potencial na entrada negativa do AO de cima é zero, logo
v O2=v 2⋅
R+R3
,e
R
v O1=−v 2⋅
R3
;
R
Como a saída do segundo estágio já foi calculada anteriormente e vale
vO=
R2
⋅(v −v )
R1 2 1
então
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
10
vO=
R2 R+2⋅R3
⋅
⋅(v 2−v 1)
R1
R
vO=
R2
2⋅R3
⋅ 1+
⋅(v 2 −v 1)
R1
R
(
)
Esta topologia apresenta alta rejeição a tensões de modo comum, ganho elevado, ganho
ajustável apenas com um resistor, impedância de entrada (diferencial e de modo comum) elevada
em ambas as entradas. Além disto se o amplificador tiver ganho unitário, somente o offset dos
amplificadores de entrada vão ser significativos na determinação do offset de saída. Se os
amplificadores de entrada forem iguais o drift na saída do amplificador fica reduzido. Nesta
configuração o primeiro estágio é responsável pelo ganho e o segundo estágio é responsável pelo
CMRR e para que este valor seja elevado o amplificador de instrumentação é comercializado em
um único integrado.
Circuitos integrados com amplificadores de instrumentação alcançam CMRR maiores do
que 100 dB (CMRR > 105), mas este valor costuma decair com a frequência. Exemplos clássicos de
amplificadores de instrumentação integrado são o AD620, AD8221 da Analog Devices, o INA118 e
o INA103 da Texas Instruments.
8.3 Amplificador de Instrumentação com Dois Operacionais
Uma versão de amplificador de instrumentação com dois AO é apresentada na figura abaixo.
A maior vantagem deste amplificador reside no uso de apenas dois AO mas esta também é sua
maior desvantagem.
Por apresentar caminhos diferentes para os sinais amplificados positiva e negativamente o
sinal sofre diferentes atrasos e deslocamentos de fase nos dois caminhos. Como resultado o CMRR
para sinais alternados é reduzido com relação ao InAmp de três AO.
Assim como no amplificador subtrator tradicional, para que este circuito funcione
apropriadamente é necessário que R1/R2 = R4/R3 o que significa que o CMRR também será
dependente do perfeito casamento de valores entre os resistores. Para contornar este problema e o
problema com o baixo CMRR em sinais alternados, este circuito pode ser encontrado integrado e,
neste caso, suas características são ajustadas de fábrica para um desempenho superior. Exemplos
deste circuito integrado são o AD627. O circuito com resistor RG permite o ajuste do ganho com a
mudança de apenas um resistor evitando que o CMRR seja afetado.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
11

v O =v 2 – v 1⋅ 1
R4 2⋅R 4

R3
RG

 
ou v O =v 2 – v 1⋅ 1
R4
R3
(sem o resistor RG).
8.4 Amplificador com Realimentação Ativa
Uma outra topologia disponível é a do amplificador para recepção de sinais de alta
frequência (Figura 8.3). Diferente dos outros amplificadores de instrumentação estes amplificadores
utilizam uma topologia de realimentação ativa. Internamente este amplificador apresenta dois pares
de entradas diferenciais sendo que usualmente uma delas é usada para a realimentação (dai o nome
realimentação ativa). Uma das vantagens deste amplificador é que seu CMRR permanece elevado
mesmo para sinais de frequência muito alta (alguns MHz) ao contrário dos amplificadores de
instrumentação tradicionais onde o CMRR cai por volta de 100 a 10kHz, dependendo do ganho e do
amplificador.
A função de transferência deste amplificador é
Vo= A⋅[(V 1 – V 2 ) – (V 3−V 4 )]
A configuração clássica para uso deste amplificador é apresentada na Figura 8.4 e apresenta
função de transferência igual à do amplificador não inversor.
Figura 8.3: Amplificador Operacional de Recepção.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
12
Figura 8.4: Configuração clássica do amplificador de instrumentação para recepção.
Exemplos deste amplificador são o AD8129 e AD8130 da Analog Devices e podem ser
utilizados em conjunto com os amplificadores operacionais diferenciais completos.
8.5 Amplificador operacional de transcondutância (OTA)
Este amplificador é muito comum em microeletrônica mas existem poucos integrados
discretos disponibilizando funções de OTA. Como o próprio nome sugere este amplificador
transforma a diferença entre as tensões de entrada em uma corrente de saída. Isto confere
características bastante interessantes a este operacional que, por exemplo, pode ter sua saída ligada
a saída de outro operacional do mesmo tipo sem problema de curto circuito.
Em microeletrônica o OTA é utilizado para produzir filtros e acionar cargas capacitivas. Os
modelos discretos apresentam uma terceira entrada, chamada de corrente de polarização, capaz de
ajustar o ganho do amplificador. A função der transferência deste operacional é dado pela equação
8.3, alguns de seus símbolos são apresentados na Figura 8.5 e o circuito interno do CA3080 é
apresentado na Figura 8.6.
i o = Ag (v + −v – )
(8.3)
Ag =gm=K⋅I B
(8.4)
onde Ag ou gm é o ganho do OTA, K é uma constante que depende do modelo e I B é a
corrente de polarização).
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
13
Figura 8.5: Símbolo do amplificador de transcondutância (OTA).
As principais aplicações para este tipo de amplificador são o controle automático de ganho,
os multiplicadores e divisores de tensão, circuitos moduladores e filtros. Apesar disto este tipo de
amplificador pode ser utilizado em praticamente todos os casos onde um operacional comum
também é utilizado. Isto, entretanto, não consiste em nenhuma vantagem pois as características do
OTA não o auxiliam nestas tarefas mais comuns. Como exemplos de OTA podemos citar o clássico
CA3080, o LM13700 e o mais recente o CA3280.
Os OTA práticos, inclusive os listados, sofrem limitações e problemas de polarização que
dificultam seu uso, sendo importante a inclusão de componentes que teoricamente não seriam
necessários. Os fabricantes explicam quais cuidados devem ser tomados com cada circuito.
Normalmente os problemas dizem respeito a não linearidades do par diferencial de entrada. Como
os OTA não precisam trabalhar realimentados a diferença entre as tensões de entrada não são zero
e, infelizmente, o par diferencial só tem comportamento linear para valores de tensão de alguns
milivolts. Circuitos com diodos e resistores são utilizados para expandir a linearidade dos
componentes. Uma coletânea de circuitos de filtros utilizando OTA foi publicada no artigo Active
Filter Design Using OTA: A Tutorial.
Figura 8.6: Circuito interno do CA3080.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
14
Exemplo 1: Mostrar que os dois circuitos a seguir apresentam impedância de entrada
(gm1·gm2·ZL) –1. Supor que todos os OTAs tem o mesmo ganho gm. Sugestão: calcule o equivalente
Thévenin para os dois circuitos – para o circuito com entrada simples calcule apenas a corrente que
entra pelo terminal v1 não nulo, para o segundo circuito determine a corrente em cada terminal e
calcule a impedância pela diferença de tensão entre as entradas v1 e v2, observe que as correntes
que entram nos terminais v1 e v2 são iguais em módulo e opostas em sentido.
Exemplo 2: Mostrar que os dois circuitos abaixo apresentam impedância de entrada gm –1.
Supor que todos os OTAs tem o mesmo ganho gm. Sugestão: calcule o equivalente Thévenin para
os dois circuitos, da mesma forma que para a questão 1.
Exemplo 3: Mostrar que os circuitos abaixo correspondem a dois amplificadores diferenciais
e um somador (de diferenças de tensão). Supor que todos os OTAs tem o mesmo ganho gm.
Sugestão: para o problema superior esquerdo e a direita use o equivalente dos exercícios anteriores,
para o problema inferior esquerdo equacione o nó da entrada negativa do operacional.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
15
8.6 Amplificador Isolador
Em muitos sistemas o ponto de medida deve ser isolado galvanicamente do restante do
circuito amplificador. Nestes casos devemos utilizar técnicas de isolação entre a etapa de potência e
a etapa de medição. Esta isolação pode ser obtida por intermédio de amplificadores isoladores.
Estes amplificadores obtém a isolação com transformadores, com capacitores ou com opto
acopladores. A relação de ganho varia de amplificador para amplificador mas o símbolo é comum a
todos e pode ser visto na Figura 8.7.
Figura 8.7: Símbolo do amplificador isolador.
As principais aplicações para este tipo de amplificador encontram-se na área médica, na
quebra de laços de terra e na diminuição dos efeitos causados por elevadas tensões de modo
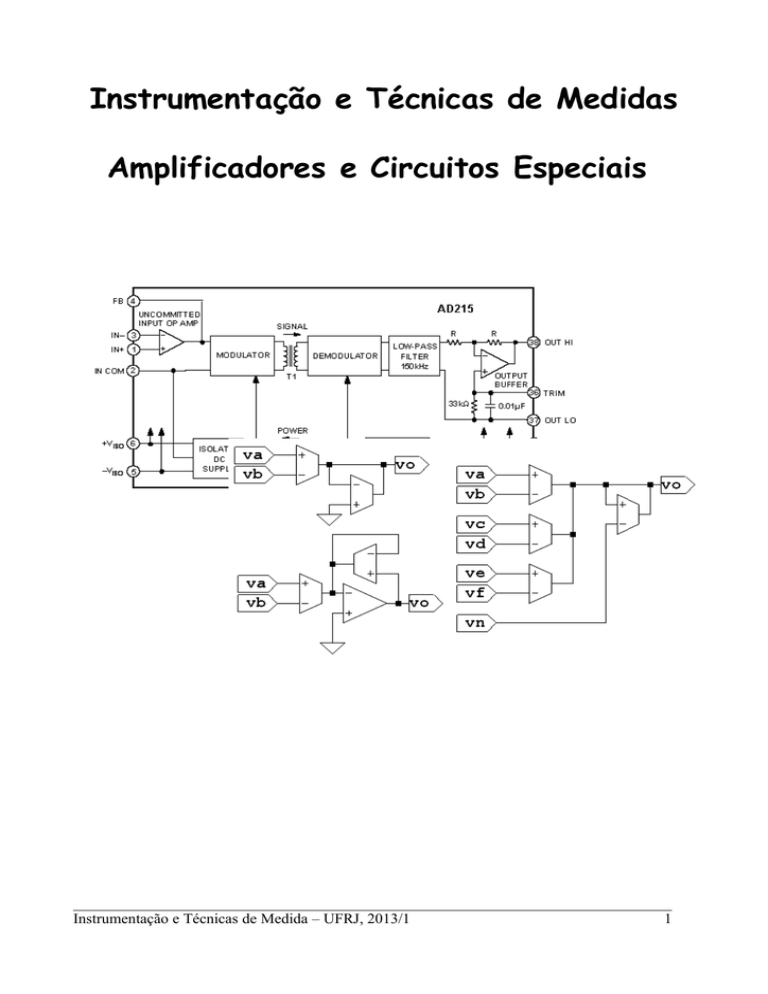
comum. Exemplos de amplificadores isoladores são o AD215 e o AD210 (com transformadores) da
Analog Devices, o ISO124 e o ISO122 (com capacitores) da Texas Instruments e o HCPL-7850,
HCPL-7851 da Avago. Outros integrados clássicos são o IS0103 e o ISO100 da Burr-Brown
(ambos obsoletos e não recomendados para novos projetos). Os diagramas de blocos para estes
amplificadores são apresentados nas figuras 8.8 e 8.9.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
16
Figura 8.8: Diagrama de blocos do AD215.
Os fabricantes fornecem duas tensões de isolação, uma para tensões continuamente
aplicadas e outra para tensões aplicadas por um curto período de tempo. A primeira tensão é menor
do que a segunda e ambas podem variar em função da frequência e temperatura. A impedância de
barreira situa-se em torno de 1012Ω.
Note que alguns destes amplificadores apresentam transformadores e portanto não são um
simples circuito integrado. Muitas vezes estes circuitos são modelos híbridos ou construídos com
componentes discretos e encapsulados em um único invólucro. Observe também que os
amplificadores isoladores necessitam de fontes de alimentação independentes para o “lado” do
amplificador. Isto significa, inclusive, dois terras diferentes e não conectados. Estes amplificadores
estão caindo em desuso e estão sendo substituídos por isoladores digitais, mais fáceis de serem
produzidos. Leia mais em Move Over Iso Amp—Make The Switch To Digital Isolation.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
17
sadf
Figura 8.9: Diagrama de blocos do amplificador IS0124.
Com os novos isoladores cada vez mais simples e com menos recursos se torna necessário
investir também em fontes de alimentação isoladas. Exemplos de conversores DC/DC são os E_T e
F_T da Mornsun, com isolação de 3000Vdc em encapsulamento SMD, os AY_D e BY_D, da
mesma fabricante com isolação de até 12000Vdc ou o ADUM6000 da Analog Devices com
isolação de 5000Vdc.
8.7 Amplificador chopper
Este tipo de amplificador foi desenvolvido a muito tempo (no fim dos anos 40, início dos
anos 50), e antes de ser um tipo de amplificador ele é uma técnica de amplificação cujo objetivo é
minimizar características indesejáveis de CC. O amplificador chopper utiliza técnicas de CA para
desacoplar as baixas frequências devido a VOS e IB. A melhora mais notável se dá no drift com a
temperatura de VOS e IOS. O amplificador chopper pode introduzir um fator de redução de 50 vezes
nestes drift. A Figura 8.10 mostra um esquema simplificado de um amplificador chopper.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
18
Figura 8.10: Diagrama esquemático de um amplificador chopper.
Na Figura 8.10 cada chave funciona como um modulador ou demodulador, uma vez que o
sinal em sua saída é equivalente ao produto do sinal de entrada por uma onda quadrada. Observe
que este é um sistema amostrado e como em todo sistema amostrado o espectro de frequências do
sinal de entrada é copiado para frequências maiores. Como o sinal de modulação é uma onda
quadrada o sinal de entrada é copiado em torno dos harmônicos ímpares da portadora. Após a
chave, na entrada do amplificador (Vy) são somados ao sinal amostrado todos os ruídos e offsets
que serão amplificados. Após a segunda chave o sinal está sincronamente demodulado (Vo) e
retorna ao seu espectro original com copias em torno dos harmônicos pares da portadora. Os offsets
são removidos pelo capacitor de saída. O espectro do ruído, por outro lado, será copiado em torno
dos harmônicos ímpares da portadora. Agora, um filtro passa baixas reconstrói o sinal original na
saída do amplificador chopper (Vout), filtrado todas as cópias espectrais de frequência elevadas.
Como este é um sistema amostrado o sinal de entrada (Vin) deve ter frequência bem menor
que a de chaveamento. Esta, por sua vez, é da ordem de centenas a milhares de Hz na maioria dos
sistemas.
Como exemplo de amplificador chopper estabilizado podemos citar o LTC1052 com
VOS < 5µV e drift de 50nV/oC. Observe que os valores de offset e drift são tão baixos que podem ser
necessários cuidados especiais na montagem do circuito. O efeito termopar causado por contatos de
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
19
metais diferentes pode produzir variações de tensão da ordem de 200nV/ oC, quatro vezes mais que
drift do LTC1052. Assim, é interessante minimizar o número de chaves, soquetes, conectores e
outros potenciais contatos problemáticos. Eletrostática e campos eletromagnéticos também podem
ser fontes de problemas. O uso de transformadores, por exemplo, podem gerar alguns microvolts de
tensão em trilhas de circuito impresso.
Os amplificadores chopper, na forma como apresentado, estão em desuso e sua produção
tem sido descontinuada. Novos amplificadores chamados de autozero (CAZ ou AZA) ou chopper
estabilizados estão em produção. Diferente do chopper tradicional os sinais são amplificados por
um canal CC, e um circuito adicional com chaveamento (chopper) é usado para remover offset e
reduzir drifts. Estas características estendem a faixa de frequência do amplificador. Exemplos de
modernos amplificadores de auto zero são o AD8571, TLC2654, OPA333. Para saber mais sobre
estes amplificadores leia To Chop or Auto-Zero: That Is the Question, da Analog Devices ou AutoZero Amplifiers Ease the Design of High-Precision Circuits, da Texas Instruments.
8.8 Amplificador Diferencial Completo
Amplificadores operacionais diferenciais completos são aqueles onde tanto a entrada quanto
a saída são diferenciais (Figura 8.11). Estes dispositivos apresentam elevados valores de CMRR,
provem baixa distorção harmônica e são aplicados na transmissão de dados a longa distância,
entradas de conversores AD ou sempre que for necessário saídas complementares.
Figura 8.11: Amplificador operacional completamente diferencial.
O circuito típico para este tipo de amplificador é apresentado na Figura 8.12. Se
R4/R3=R6/R5 a função de transferência é a mesma do amplificador subtrator porém com as saídas
complementares. Outra configuração bastante comum é aquela que transforma um sinal simples em
um sinal diferencial ( R4 =∞ , R3=0 e v –=0 ).
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
20
Figura 8.12: Amplificador subtrator.
Exemplos destes amplificadores são o ADA4940 e ADA8131 da Analog Devices e o
LTC1992 da Linear Technology LMH6550 da Texas Instruments.
8.9 Amplificador de Ganho Programável (PGA)
Amplificadores com ganhos pré estabelecidos e que podem ser selecionados digitalmente. O
tipo mais simples, apresentado na Figura 8.13, apresenta entradas digitais cuja lógica combinacional
é capaz de selecionar um entre diversos ganhos possíveis (4 no caso do PGA103). Alguns circuitos
mais sofisticados, como o MAX9939 apresentam uma interface serial (do tipo SPI) que permite
programar diversos parâmetros do amplificador. Neste caso os ganhos podem ser programados
entre 0,2 V/V e 157 V/V além de permitir a compensação de offset e oferecer recurso de shutdown
para minimizar consumo. Outros recursos comuns, internos aos PGA são os multiplexadores
(MUX) e seleção de ganhos binários ou para osciloscópio (x1, x2, x5, …). Também estão
disponíveis circuitos para ganho variável, ajustados analogicamente (VGA) como o AD8338.
Figura 8.13: Exemplo de Amplificador de Ganho Programável – PGA103
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
21
9 Circuitos Especiais
9.1 Conversores Tensão Corrente
Conversores tensão corrente são muito úteis para a implementação de fontes de corrente
controladas por tensão. A topologia mais conhecida é a Howland, mostrada na Figura 9.1 e
discutida no artigo A Comprehensive Study of the Howland Current Pump da Texas Instruments.
Observe que a principal característica destes circuitos conversores tensão corrente, ou fontes de
corrente, é que a corrente sobre a carga não depende da carga.
Figura 9.1: Conversor Tensão-Corrente tipo Howland
No circuito da esquerda, se retirarmos o resistor R, conectado a entrada vin, e o resistor RL,
o equivalente Thévenin do circuito restante resulta em uma resistência negativa de valor -R.
Substituindo o circuito pelo seu equivalente e a fonte vin em série com R pelo seu equivalente
Norton, é fácil perceber que a corrente na carga, de cima para baixo, é igual a
i RL=
vin
R
Para o circuito da direita a corrente na carga, de cima para baixo, é igual a
i RL=−
vin
R
9.1.1 Outras topologias
Além das fontes de corrente apresentada na seção anterior, na seção sobre medidas em
pontes, e nos exemplos resolvidos do primeiro capítulo, muitos outros circuitos são possíveis. A
seguir apresenta-se uma fonte de corrente Howland modificada que permite o ajuste da corrente
com a alteração de apenas 1 resistor.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
22
V 1−V 
V 1 =V − R2⋅
R1
 V 2 −V 
V 2=V −R2⋅
R1
 
 
V 1 =V⋅ 1
V 2=V 1
i0 =
V 1 −V 2
R
R2
R1
R2
R1
−V 1⋅
−V 2⋅
R2
R1
R2
R1
 
 
R2
R2
R2
R2
1
= ⋅V⋅ 1
−V 1⋅ −V⋅ 1
V 2
R
R1
R1
R1
R1
considerando que R << R2
io =

R2 V 2−V 1
⋅
R1
R

Exemplo 1: Dado o circuito abaixo, calcule sua função de transferência i L= f vi .
Considere os AO ideais. a) Estabeleça valores para os resistores R, R 3 e R4 de forma que o
circuito forneça uma corrente máxima i L máx =1 mA para uma carga 0 ≤R L ≤10 K  quando
v i =−10 V . Considere R1 =R 2 =100 K  e V CC =±12 V . Considere v i =0V . b) Calcule i L
levando em conta a existência de uma fonte de tensão conectada a entrada positiva de A1 e uma
fonte de corrente conectada a entrada positiva de A2.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
23
Solução:
Análise do circuito: A 2 : forma um amplificador de ganho unitário (buffer); A3 : forma um
subtrator junto com R3 ,R4 ; A1 : fornece a corrente de saída e é realimentado pelo subtrator através
de R1 ,R 2 .
Análise das realimentações de A1 : A1 recebe realimentação negativa (RN) através da
entrada não inversora de A3 e realimentação positiva (RP) através de A 2 e da entrada inversora
de A3 . Como o ganho dos dois caminhos do subtrator (entradas inversora e não-inversora) são
iguais em módulo, a RN é mais forte, porque a RP ainda passa pelo divisor resistivo R-R L. Como
resultado disto, o circuito possui realimentação negativa, o que permite o uso das técnicas
estudadas.
Função de transferência:
R4
R⋅i L
R3
, logo
=0
R1 +R 2
v i⋅R2 +R 1
v −A =
1
i L=−
R2⋅R3
⋅v
R1⋅R 4⋅R i
a)
Sendo i Lmáx =1 mA e R Lmáx =10K então v L Imáx =10 V (tensão máxima na carga)
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
24
R=
v Omáx −v L Imáx
, onde V Omáx é a máxima tensão de saída do AO.
i Lmáx
Como V CC =±12 V, podemos limitar, co segurança, V Omáx =11V .
R=
11 V −10 V
=1K 
1 mA
Como i L=−
então
R4
R3
R2⋅R3
⋅v (a corrente independe de RL)
R1⋅R 4⋅R i
=−
R 2⋅v i
100 K −10 
=−
=10
Ri⋅R⋅i 0
100 K⋅1K⋅1m
assim podemos escolher, por exemplo, R 4=100K  e
R3 =10K 
b)
O problema pode ser calculado por superposição:
Efeito de VOS1:
v os1 =
R1 R4
⋅ ⋅R⋅i L
R1 +R2 R3
i L  v os1 =
 R 1 +R 2 ⋅R3
v os1
R1⋅R4⋅R
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
25
Efeito de IB2:
i L =i R−i b2

R4
R⋅i R
R3
−
vA =
=0
R1 +R2
R1
1
i R=0
i L i b2 =−i b2
Portanto: i Ltot =
 R1 +R 2 ⋅R3
R1⋅R 4⋅R
v os1 −i b2
9.2 Potenciômetro Digital
Também conhecidos como digital POT, RDAC, ou digipot estes circuitos fornecem
potenciômetros integrados com passo controlado digitalmente. Eles são uma alternativa para os
circuitos PGA ou VGA e podem ser utilizados para produzir ajustes automáticos em circuitos de
instrumentação. O modelo apresentado na figura abaixo pode ter seu potenciômetro ajustado
inúmeras vezes até ser definitivamente programado pela queima de um fusível, como se fosse um
potenciômetro mecânico com eixo colado após ajustes.
9.3 Conversores AD e DA
Conversores AD (analógico para digital) e DA (digital para analógico) são muito comuns na
interface entre os mundos analógicos e digitais. Estes componentes serão estudados em detalhes no
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
26
fim deste curso mas informações adicionais podem ser obtidas em The Data Convertion Handbook
da Analog Devices. Basicamente estes componentes recebem sinais analógicos e os convertem para
digital e vice-versa aplicando um fator de conversão determinado, normalmente por tensões de
referência que devem ser fornecidas aos conversores. Estes circuitos normalmente operam com
valores digitais positivos, em complemento de dois, complemento de um, bit sinal, código de Gray
entre outros. As saídas e as entradas analógicas podem ser em tensão ou corrente. Os fatore de
escala envolvidos nesta conversão normalmente fazem com que os máximos estejam analógicos e
digitais correspondam aos valores das tensões de referência ou uma fração delas. A figura abaixo
mostra um esquema simplificado destes componentes com codificação digital monopolar.
VREF
+FS
(111...11)
MSB
Entradas
Digitais
N - Bits
N - bits
DAC
Saída
Analógica
0 ou -FS
(000...00)
LSB
VREF
MSB
+FS
(111...11)
Saídas
Dititais
N - bits
N - bits
ADC
Entrada
Analógica
0 ou -FS
(000...00)
LSB
Considerando um conversor operando com tensões positivas entre 0 e 10V e diferentes
resoluções, a tabela abaixo mostra a resolução em bits, volts, %FS e em partes por milhão (ppm) ou
dB (20·log x).
Resolução
(bits)
2N
Resolução
(10VFS)
ppm (FS)
%FS
dB (FS)
2
4
2,5V
250.000
25
-12
4
16
625mV
62.500
6,25
-24
6
64
156mV
15.625
1,56
-36
8
256
39,1mV
3.906
0,39
-48
10
1.024
9,77mV
977
0,098
-60
12
4.096
2,44mV
244
0,024
-72
14
16.384
610μV
61
0,0061
-84
16
65.636
153μV
15
0,0015
-96
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
27
18
262.144
38μV
4
0,0004
-108
20
1.048.576
9,54μV
1
0,0001
-120
22
4.194.304
2,38μV
0,24
0,000024
-132
24
16.777.216
596nV
0,06
0,000006
-144
9.4 Referências de Tensão e Corrente
Circuitos de referência de tensão ou corrente estão disponíveis para gerarem valores bastante
estáveis para alimentações de circuitos quando isto for crítico. A tabela abaixo mostra alguns destes
integrados e suas características principais.
Parâmetro
Saída
(V/mA)
Drift c/ Tempo
(10-6/1000h)
Drift Térmico
(10- 6/K)
Regulação (V)
(10-6/V)
Regulação (I)
(10-6/mA)
Ruído (μVpp)
(0,1- 10Hz)
AD581L
LM399A
LT1021A
MAX671C
REF10A
REF102C
10/10
6,95/10
10/10
10/10
10/20
10/10
25
20
15
50
50
5
5
0,6
2
1
8,5
2,5
50
10
4
50
100
100
50
3
25
1
800
10
40
6
6
50
30
5
Seleção de componentes do livro Sensors and Signal Conditioning
Uma lista de referências fabricadas pela Linear Technology pode ser obtida no seu AN42 –
Voltage Reference Circuit Collection.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
28