Técnicas de apoio à Economia (TAE) população amostra Critérios

Ex:
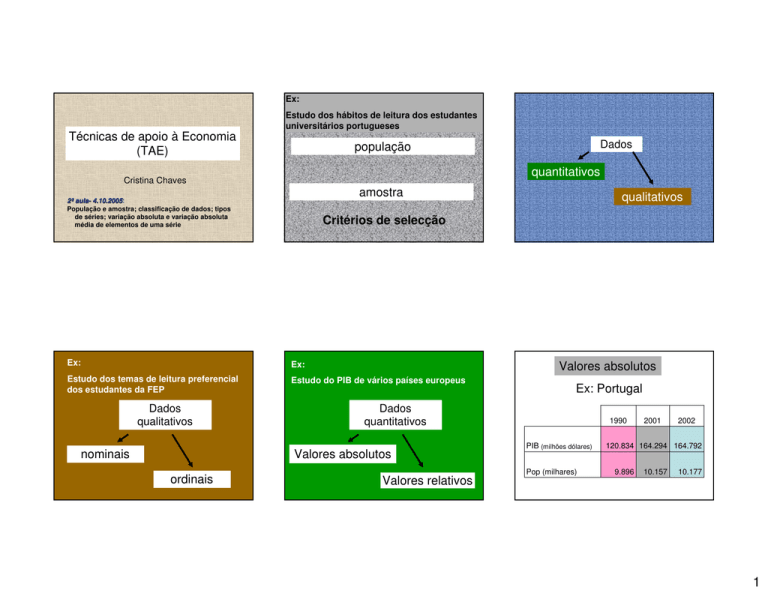
Técnicas de apoio à Economia
(TAE)
Estudo dos hábitos de leitura dos estudantes
universitários portugueses
quantitativos
Cristina Chaves
amostra
2ª aulaaula- 4.10.2005:
4.10.2005
População e amostra; classificação de dados; tipos
de séries; variação absoluta e variação absoluta
média de elementos de uma série
Ex:
Estudo dos temas de leitura preferencial
dos estudantes da FEP
Estudo do PIB de vários países europeus
Valores absolutos
ordinais
Ex: Portugal
Dados
quantitativos
Valores absolutos
nominais
qualitativos
Critérios de selecção
Ex:
Dados
qualitativos
Dados
população
Valores relativos
1990
PIB (milhões dólares)
Pop (milhares)
2001
2002
120.834 164.294 164.792
9.896
10.157
10.177
1
Valores relativos
Ex: PIB pc (dólares)
País
1990
PIB pc (dólares)
2001
2002
Séries de dados
País
1990
2001
2002
Alemanha
20.139
24.085
24.004
Áustria
20.758
25.892
25.880
24.418
Bélgica
20.526
24.421
24.418
27.001
27.404
Dinamarca
22.407
27.001
27.404
14.607
18.755
19.005
Espanha
14.607
18.755
19.005
Finlândia
19.849
23.012
23.193
Finlândia
19.849
23.012
23.193
França
20.282
23.601
23.844
França
20.282
23.601
23.844
Grécia
12.430
15.951
16.579
Holanda
20.178
25.507
25.778
Alemanha
20.139
24.085
24.004
Áustria
20.758
25.892
25.880
Bélgica
20.526
24.421
Dinamarca
22.407
Espanha
temporais
Grécia
12.430
15.951
16.579
Holanda
20.178
25.507
25.778
Irlanda
14.049
29.106
32.204
Irlanda
14.049
29.106
32.204
Itália
19.987
23.258
23.408
Itália
19.987
23.258
23.408
Luxemburgo
28.596
52.663
54.201
Luxemburgo
28.596
52.663
54.201
Portugal
12.210
16.175
16.193
Portugal
12.210
16.175
16.193
Reino Unido
18.794
22.895
23.166
Reino Unido
18.794
22.895
23.166
Suécia
19.386
22.712
23.071
Suécia
19.386
22.712
23.071
União Europeia
18.996
22.704
22.811
União Europeia
18.996
22.704
22.811
Portugal
1990
PIB
(milhões)
1991
1992
seccionais
Séries temporais (t)
...
2001
2002
Variação absoluta
120.834 125.832 126.612 ... 164.294 164.792
De um período:
Conceito de variação absoluta
Séries temporais (t)
De k períodos:
∆x t +1, t = x t +1 − x t
Variação absoluta média
.
De k períodos:
∆x t + k , t = x t + k − x t
∆ m x t + k,t =
x t + k,t
k
=
x t +k − x t
k
2