Minha resposta

O que são polígonos semelhantes? Os triângulos são um caso particular de
polígonos semelhantes. O que são triângulos semelhantes?
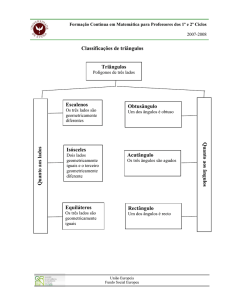
Polígonos Semelhantes
Dois polígonos com o mesmo número de lados dizem-se semelhantes quando têm de um
para o outro:


Ângulos geometricamente iguais;
Lados correspondentes proporcionais.
A razão de semelhança de dois polígonos semelhantes é a razão entre dois lados
correspondentes:



Se a razão é maior que 1, então, estamos perante uma ampliação;
Se a razão é menor que 1, então, estamos perante uma redução;
Se a razão é igual a 1, então, as figuras são geometricamente iguais.
Exemplo: Observe agora os seguintes retângulos, será que eles são semelhantes?
Como as duas figuras são retângulos, então, a amplitude todos os ângulos internos é
90º, logo, os ângulos são geometricamente iguais.
Logo, os lados são diretamente proporcionais.
Deste modo, podemos afirmar que as duas figuras são semelhantes.
A razão de semelhança é 1,5.
Semelhança de Triângulos
Na Geometria Plana é dito que dois triângulos são semelhantes quando
guardam uma proporção entre eles, ou melhor, quando os ângulos e os lados do
primeiro triângulo estão em correspondência com os ângulos e lados do segundo
triângulo, de tal forma que seus ângulos sejam iguais e os lados do primeiro triângulo
sejam proporcionais aos lados do segundo.
Mas, de fato não é necessário que se conheça todos os lados e ângulos dos
triângulos para que tenhamos a semelhança assegurada. É isso que nos dizem os
critérios de semelhança de triângulos: AA, LAL, LLL.
Caso AA - Ângulo Ângulo
"Se dois triângulos possuem dois ângulos ordenadamente congruentes, então eles são
semelhantes."
Caso LAL - Lado Ângulo Lado
"Se dois triângulos possuem os seus lados homólogos proporcionais, então eles são
semelhantes."
Caso LLL - Lado Lado Lado
“Se dois triângulos possuem os seus lados homólogos proporcionais, então eles são
semelhantes."
Que medidas terão a cabana do Tom sabendo que a razão de semelhança é
1:2?
A base medirá 3m, e os lados terão 2,25 m cada um, a entrada terá 50cm de largura e
1m de altura. Os ângulos continuarão com a mesma medida, pois os triângulos são
semelhantes, e 2 triângulos semelhantes possuem os mesmos ângulos.
Cálculos:
6/2 = 3
4.5/2 = 2.25
1 / 2 = 0.5
2/2 = 1
Tales de Mileto foi o primeiro personagem conhecido a quem se associam
descobertas matemáticas. Como foi que este matemático determinou a altura
da pirâmide de Quéops?
Há duas versões para este fato. Hicrônimos, discípulo de Aristóteles, diz que Tales
mediu o comprimento da sombra da pirâmide no momento em que nossas sombras são
iguais a nossa altura, assim medindo a altura da pirâmide. A de Plutarco diz que
fincando uma vara vertical no extremo da sombra projetada pela pirâmide,
construímos à sombra projetada da vara, formando no solo dois triângulos
semelhantes.
Notamos que neste relato é necessário o conhecimento de teoremas sobre triângulos
semelhantes.
Observando o desenho abaixo, a vara colocada no extremo C da sombra da pirâmide
forma, com sua sombra, o triângulo DCE que é semelhante ao triângulo ABC.
Medindo as duas sombras e a altura da vara, pode-se determinar então a altura da
pirâmide
Conclusão:
Essas atividades mostram como a matemática tem aplicação no dia á dia, pois usando
semelhança de triângulos, Tales pode medir uma grande pirâmide, como também
podemos medir a altura de muitas outras coisas como árvores, prédios, e até a nós
mesmos.
Referências
http://www6.ufrgs.br/espmat/disciplinas/geotri/moduloII/conteudos2_criterios1.html
http://www.matematica.br/historia/calpiramide.html