ESCOLA MAGNUS DOMINI
O ESTUDO DO TRIÂNGULO RETÂNGULO E SUA APLICABILIDADE NA
ENGENHARIA
Adriano Oliveira Vigário Filho
Maria Fernanda Bonvechio de Oliveira
Marina Slompo
MARINGÁ
2016
1. INTRODUÇÃO
Este trabalho visa mostrar as pessoas a importância do triângulo
retângulo nas edificações de hoje em dia e de antigamente, indicando
principalmente a sustentação das edificações. Para comprovar este teorema,
há demonstrações e um tangran no qual prova que a² = b² + c².
O Teorema de Pitágoras é considerado uma das principais descobertas
da Matemática, ele descreve uma relação existente no triângulo retângulo. Vale
lembrar que o triângulo retângulo pode ser identificado pela existência de um
ângulo reto, isto é, medindo 90º. O triângulo retângulo é formado por dois
catetos e a hipotenusa, que constitui o maior segmento do triângulo e é
localizada oposta ao ângulo reto. Em qualquer triângulo retângulo, o quadrado
do tamanho da hipotenusa é igual à soma dos quadrados dos tamanhos dos
catetos, ou seja, a² = b² + c², como dito anteriormente.
2. TEOREMA DE PITÁGORAS
Pitágoras foi um importante matemático e filósofo grego. O seu teorema
é considerado uma das principais descobertas de toda a matemática, ele
descreve uma relação existente no triângulo retângulo.
Um dia quando estava visitando o Egito, Pitágoras se encantou com as
pirâmides e desenvolveu o seu famoso teorema, que é muito utilizado na
matemática. O seu teorema diz que podemos calcular um lado do triângulo
retângulo sabendo os outros dois. Segundo Pitágoras, a soma dos quadrados
dos catetos é igual ao quadrado da hipotenusa.
Podemos reparar que suas invenções são aplicadas até nos dias de
hoje. Outra curiosidade é que o filosofo deu origem a uma corrente, que
inspirou vários pensadores gregos, entres eles, Platão. Sua corrente vem de
sua escola, a escola Pitagórica, que influenciou muito os ideias, e
principalmente os filósofos.
Também podemos citar o uso do teorema de Pitágoras aplicado no
estudo da trigonometria, por meio de sua aplicação determinamos valores de
medidas desconhecidas. Na trigonometria, após o teorema de Pitágoras ser
aplicado, descobriremos os três lados do triangulo retângulo, o qual facilitará a
continuação nas aplicações da trigonometria pelo fato de que elas precisam
das medidas dos lados A, B, C no triangulo retângulo.
Podemos afirmar que qualquer obra de construção civil requer o mínimo
de conhecimento matemático, no qual um dos mais utilizados é o teorema de
Pitágoras. Desde o início da obra, em sua demarcação inicial até o
acabamento, colocação dos pisos, muitas vezes, os pedreiros utilizam ângulos
retos aplicando então o teorema de Pitágoras. Uma curiosidade é que para os
pedreiros o ângulo reto de teorema é chamado de “deixar no esquadro”.
Na fase do acabamento da construção, durante a colocação dos pisos, o
pedreiro utiliza cálculo de áreas, ângulos e retas, e as quatro operações
básicas que estão presentes em quase todo desenvolvimento da construção.
Após os exemplos citados, podemos chegar à conclusão que a
matemática e o princípio do teorema é utilizado a todo momento na construção
civil. A matemática nesta profissão é uma ligação entre a teoria e a prática.
Teorema significa “afirmação que se pode provar. Vale lembrar que o
triângulo retângulo pode ser identificado pela existência de um ângulo reto, isto
é, medindo 90º. O triângulo retângulo é formado por dois catetos e a
hipotenusa, que constitui o maior segmento do triângulo e é localizada oposta
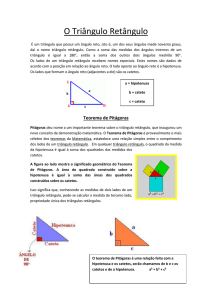
ao ângulo reto, podemos analisar isto na Imagem 1. O Teorema afirma que “a
soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”. Em
qualquer triângulo retângulo esta regra se aplica. É possível utilizar a regra de
Pitágoras em praticamente todas as figuras geométricas planas, pois, de
alguma forma elas podem ser divididas em triângulos.
Imagem 1 – Triângulo Retângulo (a = hipotenusa b = cateto c = cateto)
2.1 Elementos dos triângulos
Para entendermos o teorema de Pitágoras melhor temos que entender
antes a estrutura dos triângulos. Um triângulo é um polígono que possui: três
lados, três vértices e três ângulos internos e sua classificação é feita
considerando seus lados ou seus ângulos. Há três tipos de triângulos, sendo
eles: equilátero, isósceles e escaleno.
Triângulo Equilátero é todo triângulo que apresenta os três lados com a
mesma medida, congruente. Já o Triângulo Isósceles é todo triângulo que
apresenta dois lados com a mesma medida. E o Triângulo Escaleno é todo
triângulo que apresenta os três lados com medidas diferentes.
Também podemos classificar os triângulos de acordo com a medida de
seus ângulos internos, sendo eles: triângulo acutângulo, triângulo retângulo e
triângulo obtusângulo.
O Triângulo acutângulo é todo triângulo que apresenta os três ângulos
internos menores que 90o, ou seja, os três ângulos internos são agudos. E o
Triângulo obtusângulo é todo triângulo que apresenta um ângulo interno maior
que 90o, ou seja, que possui um ângulo obtuso. Já o Triângulo retângulo é todo
triângulo que apresenta um ângulo interno reto, ou seja, que possui um ângulo
medindo 90o. As propriedades dos triângulos variam de acordo com suas
classificações.
2.2 Aplicabilidade do Teorema de Pitágoras
Para poder apresentar o teorema de Pitágoras nos dias de hoje primeiro
temos que destacar as construções antigas e seu uso nas pirâmides, onde é
ele que as sustenta matematicamente.
Antigamente a geometria na babilônia se relacionava com a mensuração
prática. Eles deviam estar familiarizados com as regras gerais de cálculo da
área do triângulo retângulo.
Já nos dias de hoje podemos visualizar com maior evidência o triângulo
retângulo nas construções e edificações. Sua aplicação é importante nas
edificações pois ele “sustenta-as” com seu ângulo reto, como por exemplo, as
paredes, os telhados entre outros.
3. DEMONSTRAÇÕES QUE PROVAM O TEOREMA DE PITÁGORAS
Apresentamos, a seguir, a demonstração desta fórmula: a² = b² + c².
Primeiro iremos imaginar uma reta que irá sair do vértice "A", que possui o
ângulo reto, de maneira perpendicular em direção ao lado "a" e diremos que o
ponto de encontro dessa reta com esse lado se chamará "D". Note que a reta é
a altura do triângulo, ela mede "h". Note também que depois que o lado "a"
ficou dividido em dois pedaços, esses pedaços medem "m" e "n". Os vértices
"B" e "C" possuem os ângulos medindo "x" e "y". Assim, "x + y = 90º" olhando
para o triângulo ABC (maior). Podemos ainda preencher os dois triângulos
menores ABD e ADC pelos ângulos que faltam, que no caso serão "x" e "y",
como indica a Imagem 2.
Imagem 2 – Demonstração da Fórmula
A Imagem 2 nos permite deduzir que os triângulos ABC, ABD e ADC são
semelhantes entre si e isso nos permite fazer algumas relações matemáticas
com seus lados (Imagem 3).
Imagem 3 – Relações matemáticas com os lados do triângulo retângulo
Sabemos que b² = a•n e que c² = a•m então se somarmos b² com c²
seria o mesmo que estarmos somando a*n com a*m já que são iguais. Iremos
fazer isso para ver o que acontece, veja: b² + c² = a•n + a•m. Isolando o "a" do
segundo membro temos que: b² + c² = a•(m+n). Logo o resultado final será:
b² + c² = a•(m+n)
b² + c² = a•a
b² + c² = a²
ou
a² = b² + c²
3.1 Aplicação do Teorema de Pitágoras
Podemos utilizar esse teorema para facilitar o cálculo da diagonal de um
quadrado e altura de um triângulo equilátero (triângulo com os lados iguais). A
relação dos números irracionais com o Teorema de Pitágoras consiste no
cálculo da medida da diagonal do quadrado.
Dado o quadrado ABCD com lados medindo 1 unidade, vamos
determinar a sua diagonal, representada por ‘d’ na Imagem 4. A diagonal divide
o quadrado em dois triângulos retângulos, sendo assim, podemos notar que a
diagonal do quadrado é a hipotenusa dos dois triângulos retângulos. Aplicando
o Teorema de Pitágoras, temos:
Imagem 4 – Observação da Diagonal
Com o passar dos séculos e a evolução da Matemática, os números
irracionais foram aceitos e introduzidos nos conceitos matemáticos, tornando o
Teorema de Pitágoras ferramenta imprescindível nos estudos relacionados à
Geometria.
4. CONCLUSÃO
Pitágoras foi um importante matemático e filosofo grego e seu teorema
foi considerado uma das grandes e principais descobertas na matemática. Ele
descobriu esse teorema quanto estava no Egito observando as pirâmides. Seu
teorema nos possibilita descobrir um dos lados do triangulo retângulo tendo os
outros dois, como mostra na fórmula do teorema a² = b² + c². Mas a fórmula do
teorema só é válida quando aplicada em um triangulo retângulo, onde se
encontra o ângulo reto (90°).
Apesar de ser um conceito antigo, o Teorema de Pitágoras continua a
ter utilização prática no nosso dia a dia, sendo bastante utilizado para cálculos
de medidas em projetos arquitetônicos ou de engenharia, possibilitando a
execução segura dessas obras. Vale ainda citar, a utilização do triângulo como
base de apoio para diversos móveis, cadeiras, objetos e também construções,
situação em qual o ângulo reto é fundamental e imprescindível para manter a
estabilidade desses elementos.
REFERÊNCIAS
http://blogdoenem.com.br/triangulos-definicoes-e-propriedades-geraismatematica-enem/
http://brasilescola.uol.com.br/mitologia/pitagoras.htm
http://dspace.bc.uepb.edu.br/jspui/handle/123456789/3993
http://escolakids.uol.com.br/classificacao-dos-triangulos.htm
http://mundoeducacao.bol.uol.com.br/matematica/o-teorema-pitagorasaplicado-no-estudo-trigonometria.htm
http://www.brasilescola.com/matematica/propriedades-triangulo-retangulo.htm
http://www.infoescola.com/filosofos/pitagoras/
http://www.matematica.br/historia/babilonia.html
http://www.suapesquisa.com/pesquisa/pitagoras.htm
https://abordandoamatematica.wordpress.com/2015/09/24/a-matematica-naconstrucao-civil/