Aula 02 - Daves - Sistema Númerico e Representação interna

ARQUITETURA DE
COMPUTADORES
Sistema de Numeração
Prof Daves Martins
Msc Computação de Alto Desempenho
Email: [email protected]
Sistemas Numéricos
• Principais sistemas numéricos:
• Decimal
• 0, 1, ..., 9
• Binário
• 0, 1
• Octal
• 0, 1, ..., 7
• Hexadecimal
• 0, 1, ..., 9, A, B, C, D, E, F
•É importante atentar que no sistema
hexadecimal, as letras de A até F
equivalem, em decimal, a 10, 11, 12, 13,
14 e 15, respectivamente
Conversão Base X – Base 10
• Processo: soma de multiplicações
• numd = anxn + an-1xn-1 + ... + a0x0
• Exemplos, converter para a base
10:
• 10112
• 4A3B16
•72718
Conversão Base X – Base 10
• numd = anxn + an-1xn-1 + ... + a0x0
• Binário – Decimal: 10112
• 1 * 23 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0
• 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 = 1110
• Octal– Decimal: 72718
• 7 * 8 3 + 2 * 82 + 7 * 8 1 + 1 * 8 0
• 7 * 512 + 2 * 64 + 7 * 8 + 1 * 1 = 376910
• Hexadecimal – Decimal: 4A3B16
• 4 * 163 + A * 162 + 3 * 161 + B * 160
• 4 * 163 + 10 * 162 + 3 * 161 + 11 * 160
• 4 * 4096 + 10 * 256 + 3 * 16 + 11 * 1 =
1900310
Conversão Base X – Base 10
• Exercícios, converter para a base
10:
• 11002
• 01112
• ABCD16
•A8B216
Respostas
•Respostas ao exercício anterior:
• 11002 = 12 10
• 01112 = 7 10
• ABCD16 = 43981 10
•A8B216 = 43186 10
Conversão Base 10 – Base X
• num1d
r1
x
num2d
r2
x
num3d
numn-1d
rn-1
numix = rnx...r2xr1x
x
rn
Conversão Base 10 – Base X
• Exemplo, converter 5310 para binário:
53 2
Momento de Parar: quando
1 26 2
o quociente é menor do que
0 13 2
o valor da base
1 6 2
Neste caso, o valor da base
0 3 2
é “2”
1 1
1101012
Conversão Base 10 – Base X
• Exemplo, converter 101610 para hexadecimal:
1016 16
8 63 16
15
3
3F816
•Exemplo, converter 5310 para hexadecimal:
53 16
5 3
3516
Conversão Base 10 – Base X
• Exercícios, converter da base 10:
• para binário, 25
• para hexadecimal, 156
Conversão Base 10 – Base X
• Respostas
• 25 10 = 11001
• 156 10 = 9C 16
2
Adição e subtração em binár
– Somamos por colunas à partir da direita, temos
8+5=13, como a soma excedeu o maior dígito
disponível, usamos a regra do transporte para a
próxima coluna.
– Assim, dizemos que dá 3 e “vai um”.
– Este transporte “vai um” é computado na soma
da próxima coluna, que passa a ser 8+1+1=10,
novamente usamos o transporte e dizemos que
dá 0 e “vai um” abrindo uma nova coluna que é
0+0+1=1.
– Obtemos desta forma o resultado 103.
Adição e subtração em binár
• Vamos agora para o sistema base 2,
como temos apenas dois dígitos, vamos
verificar quais os possíveis casos que
ocorrerão na soma por colunas:
0
+0
0
a)
b)
0
+1
1
1
+0
1
c)
1
+1
10
d)
e) 1
1
+1
11
• Nos casos “a”,”b” e “c” não houve
transporte.
Adição e subtração em binár
• No caso “d” houve transporte, o resultado
é 0 e “vai um” e no caso “e” realizamos a
soma de três parcelas incluindo um
transporte, o resultado é 1 e “vai um”.
• Vamos agora efetuar 11012+10112,
temos:
1 1 1
1101
+1011
11000
Adição e subtração em binár
• Outro exemplo, efetuar 111012 + 10012
1
1
11101
+ 1001
100110
• Ainda outro exemplo, efetuar 1012+1112+102
1
1
101
111
+ 10
1110
Adição e subtração em binár
• Subtração no sistema binário
• Como o método também é análogo ao da
subtração no sistema decimal, vamos ver
quais os possíveis casos que ocorrerão
na subtração por colunas.
a)
0
-0
0
b)
0
-1
1
c)
1
-0
1
d)
1
-1
0
Adição e subtração em binár
• No caso “b”, o resultado será 1, mas
ocorrerá um transporte para a coluna
seguinte, que deve ser acumulado no
subtraendo.
• Exemplificando,
vamos efetuar 11102 – 10012
1110
1
-1001
0101
Adição e subtração em binár
• Outro exemplo,
vamos efetuar 11000- 101
11000
1
1
1
-
101
10011
• Multiplicação no sistema binário
• Novamente análoga ao caso decimal.
Agora os casos possíveis são:
a) 0x0 = 0 b) 0x1 = 0 c) 1x0 = 0 e d)
1x1 = 1
Adição e subtração em binár
• Exemplificando, efetuar 111102 x 112
11110
x 11
1 1 1
11110
11110+
1011010
Adição e subtração em binár
• Outro exemplo, efetuar 11012 x 102
1101
x 10
0000
1101+
11010
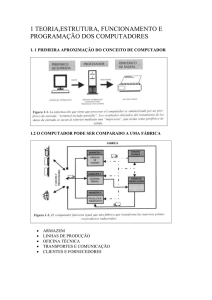
Tipos de dados tratados
pelo computador
• Dados e as instruções
armazenados em memória
– são codificados sob a forma de sinais
elétricos do tipo ligado e desligado
• representado pelos números 1 e 0
• sistema binário
– cada unidade de informação é
chamada de bit
• abreviação de Binary digit
Tipos de dados tratados
pelo computador
• Unindo dois ou mais bits
– Um bit pode representar dois valores: 1 ou 0, ou
então verdadeiro ou falso
– Pode-se unir dois ou mais bits para representar
mais de dois valores
• quantidade de valores representáveis por uma
sequência de n bits é de 2n
– Algumas strings de bits têm nomes próprio:
•
•
•
•
•
uma sequência de 8 bits são chamados de byte
uma sequência de 4 bits é chamada de nibble
um grupo de 16 bits é chamado de word
um grupo de 32 bits é chamado de double word
um grupo de 64 bits é chamado de quad word
Tipos de dados tratados
pelo computador
• K = 1024
– Na vida cotidiana e na física, o "k" vale 1000
• 1 km = 1000 metros
• 1 kg = 1000 gramas
• 1 kV = 1000 volts
– Número 1024 foi o escolhido para representar o "k" da
computação
• por razões de simplificação de hardware
• M = 1024 K
– "M" normalmente vale 1.000.000, na computação vale:
• 1 M = 1024 k = 1024x1024 = 1.048.576
• G = 1024 M
– "G" que normalmente vale 1 bilhão, na computação vale
• 1 G = 1024 M = 1024x1024x1024 = 1.073.741.824
Representação de
Caracteres
• Um caractere normalmente é representado por um
byte
– maioria dos códigos alfanuméricos representam caractere
através de um byte
– código ASCII a letra 'A' é representada pelo byte “0100
0001“
– uma sequência de caracteres é expressa por uma cadeia
de bytes sucessivos
– Nem todos os tipos de códigos utilizam os 8 bits de um
byte para a representação de caracteres
•
Representação de
Caracteres
Código de 7 bits (ASCII)
– apareceu com as linguagens de alto nível
Representação de
Caracteres
• ASCII Estendido
– caracteres extras representam caracteres de línguas
mortas e caracteres especiais para desenhas figures
Representação Interna de
Números
• Representação de Números Inteiros
– Representação de números não sinalizados
• utiliza-se normalmente o valor do próprio número binário
– número 6 é representado por 0101
– número 12 é representado por 1100
– Representação de números sinalizados
•
•
•
•
módulo e sinal (MS)
complemento de 1 (C-1)
complemento de 2 (C-2)
excesso de 2 elevado a (N-1)
Representação Interna de
Números
• Módulo e Sinal (MS)
– Bit que está situado mais à esquerda representa o
sinal
• valor será 0 para o sinal + e 1 para o sinal -
– Bits restantes (N-1) representam o módulo do número
– Exemplo
• supondo que exista a limitação de 8 bits (N=8)
– valor 00101010 representa o número +42
– valor 10101010 representa o número -42
– Amplitude (faixa) de representação para N bits
•
•
•
•
-2N-1+1 ≤ X ≤ 2N-1-1
Para 8 bits (byte): -127 ≤ X ≤ 127
Para 16 bits (word): -32767 ≤ X ≤ 32767
Para 32 bits (double word): -2147483647 ≤ X ≤ 2147483647
Representação Interna de
Números
• Módulo e Sinal (MS)
– Vantagem deste sistema
• possuir faixa simétrica
– Deficiências
• possui duas representações para o número 0
– para 8 bits: 00000000 (+0) e 1000000 (-0)
– Problema da Soma
Representação Interna de
Números
• Vamos ver alguns exemplos:
– Representar em binários sinal-módulo os números
2310 , -1510 , 1110 e -910 usando palavras de 8 bits.
2310 = 101112 usando 8 bits temos: 000101112
1510 = 11112 usando 8 bits temos: 000011112
como o sinal é negativo vem –1510 = 100011112.
1110 = 10112 usando 8 bits temos: 000010112
910 = 10012 usando 8 bits temos: 000010012 ,
como o sinal é negativo vem –910 = 100010012
Representação Interna de
Números
• Complemento de 1 (C-1)
– Utiliza o bit mais à esquerda para o sinal
• 0 ao sinal + e o 1 ao sinal -
– Números positivos
• N-1 bits da direita representam o módulo (como no MS)
– Números negativos
• obtidos pelo complemento de todos os seus dígitos
(trocando 0 por 1 e vice-versa) incluindo o bit de sinal
– Exemplo
• supondo que exista a limitação de 8 bits (N=8)
• valor 00101010 representa o número +42
• valor 11010101 representa o número -42
Representação Interna de
Números
• Complemento de 1 (C-1)
– Mesma faixa de representação para N dígitos do
método MC
• -2N-1+1 ≤ X ≤ 2N-1-1
– Desvantagem
• tem duas representações para o número 0
– 00000000 (+0) e 11111111 (-0)
Representação Interna de
Números
Ocorre porque há duas representações para
o zero: -0 e +0
Representação Interna de
Números
Representação Interna de
Números
• 1 + 255 = 0
• Significa que...
• 0 – 1 = 255 ( 11111111b)
• E que...
• 0 – 2 = 254 (11111110b)
• 0 – 3 = 253 (11111101b)
• 0 – 4 = 252 (11111100b)
• ...
• 0 – 127 = 129 (10000001b)
• 0 – 128 = 128 (10000000b)
Representação Interna de
Números
• Complemento de 2 (C-2)
– Utiliza o bit mais à esquerda para o sinal
• 0 ao sinal + e o 1 ao sinal -
– Números positivos
• N-1 dígitos da direita representam o módulo
– Números negativos
• executa-se o Complemento de 1: obtém-se o complemento de
todos os bits do número positivo (trocando 0 por 1 e vice-versa)
incluindo o bit do sinal
• Ao resultado obtido soma-se 1 (em binário), desprezando-se o
último transporte (se existir)
– O mais utilizado para representar números negativos
Representação Interna de
Números
• Por questões de convenção e eficiência, utiliza-se a
notação de complemento a 2 para se trabalhar com
números binários no computador
• Utilizando esta notação, a subtração é uma soma. Por
exemplo: 7 – 5 seria 7 + (-5)
• Embora seja uma alteração sutil, faz uma enorme diferença
para o computador
• Números que tenham o bit mais à esquerda 1 são
negativos. Os que tiverem 0 neste bit, serão positivos
• Para trabalhar com complemento a 2, é necessário saber a
quantidade de bits que os números devem ter. Isto varia de
acordo com o processador. Caso o resultado exceda esta
quantidade de bits, o bit mais à esquerda é desprezado
• Deve-se proceder da seguinte maneira:
– Os números negativos devem ter seus bits invertidos
– Soma-se 1 ao valor obtido
Representação Interna de
Números
• Complemento de 2 (C-2)
– Faixa de representação é assimétrica (inconveniente)
• -2N-1 ≤ X ≤ 2N-1-1
• Para 8 bits (byte): -128 ≤ X ≤ 127
• Para 16 bits (word): -32768 ≤ X ≤ 32767
• Para 32 bits (double word): -2147483648 ≤ X ≤ 2147483647
– Vantagem
• uma única representação para o número 0
• Para 8 bits, teremos: 00000000
Representação Interna de Números
• Complemento de 2 (C-2)
39
Representação Interna de Números
40
Representação Interna de Números
Exemplo
• Faça 10 – 5 utilizando complemento a 2. Suponha
que seu processador trabalhe com números de 5
bits
• Na verdade, deve-se fazer 10 + (-5)
• 10, em binário é: 01010
• 5 em binário é: 00101
• Aplicando o complemento a 2, obteremos -5:
– 00101. Invertendo seus bits, temos: 11010
– Fazendo 11010 + 1, temos 11011
• Agora, basta somar: 01010 + 11011. Assim,
obtemos 100101. Como o processador é de 5 bits,
o bit mais à esquerda a mais será desprezado.
Assim, o número que obtive como resultado foi
00101. De fato, o resultado é 5.
Representação Interna de Números
• Vamos exemplificar obtendo os
complementos de 2 dos números binários
abaixo:
binário
10001001
00111100
10011111
11000101
01101011
compl de 1
01110110
11000011
01100000
00111010
10010100
compl de 2
01110111
11000100
01100001
00111011
10010101
• Exercícios
•
Efetue as operações binárias
a)
d)
f)
i)
•
10001+1111 b) 1110+1001011
110101+1011001+1111110
10101-1110 g) 100000-11100
11001x101 j) 11110x110
c) 1011+ 11100
e) 1100+1001011+11101
h) 1011001-11011
k) 11110x111
Represente os números em notação sinal-módulo 8bits
a) 97
b) -121
c) 79
d) -101
• Represente os números do exercício anterior em
complemento de 2.
• Efetue as operações utilizando complemento de 2.
a) 111100-11101011
b) 101101-100111
c) 758-308
Overflow e underflow
• Os números manipulados
– grande demais para ser representados provocam
um overflow.
– pequeno demais para ser representados provocam
um underflow.
• Os sistemas têm feedback diferentes em caso de over
ou underflow. Certos param a execução, certos dão
uma mensagem e outros representam o número de
uma forma especifica.
Notação em Ponto
Flutuante
•
•
•
•
•
•
•
Como guardar esse número?
65340000000000000000000000000000
Pode ser reescrito assim:
6,534 * 10+31
O que significa * 10+31 ?
Significa que tenho que mudar a vírgula de lugar para
obter o número real
No caso, preciso andar 31 casas à direita
Notação científica ou Notação em Ponto Flutuante
Notação em Ponto
Flutuante
•
•
•
•
•
•
É comum especificar esses números assim:
6,534 * 10+31 → 6,534E31
6,534 * 10-31 → 6,534E-31
Repare que essa representação tem 3 partes
6,534E-31
Quais são os nomes destas partes?
6,534E-31
• Característica
• Mantissa
• Expoente
Notação em Ponto Flutuant
Intervalo normalizado aproximado: 2–126 a 2127.
também chamado de short real.
Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007.
Notação em Ponto Flutuant
•
•
•
Sinal
– 1 = negativo, 0 = positivo
Significando
– Dígitos decimais à esquerda e à direita do ponto decimal
– Notação posicional ponderada
– Exemplo:
123.154 = (1 x 102) + (2 x 101) + (3 x 100) + (1 x 10–1)
+ (5 x 10–2) + (4 x 10–3)
Expoente
– Inteiros sem sinal
– bias inteiro (127 para precisão simples)
Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007.
Notação em Ponto Flutuant
Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007.
Notação em Ponto Flutuant
• A mantissa é normalizada quando um 1
aparece à esquerda do ponto binário
• Não-normalizado: o ponto binário pode variar
até que o expoente seja zero
• Exemplos
Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007.
50
Notação em Ponto
Flutuante
•
•
•
•
Será que isso funciona com binários?
10110000000000000000000000000000b
Pode ser reescrito assim:
1,011b * 2+31
Assumimos que a característica é sempre 1b
Notação em Ponto
Flutuante
Notação em Ponto
Flutuante
Conversão números
fracionários/binário e
binários/fracionários
Notação em Ponto
Flutuante
Conversão números
fracionários/binário e
binários/fracionários
Notação em Ponto
Flutuante
• Vamos representar o número 2,25 nessa
notação
• Primeiro vamos converter para binário
• Parte inteira:
• 2 = 10b
• Parte fracionária:
• 0,25 = 0,01b
• Logo... 2,25 = 10,01b
• Em notação científica:
• 10,01b = 1,001b * 21
Notação em Ponto
Flutuante
•
•
Usar 8 bits é didático, mas muito limitado
para a prática
•
Até meados dos anos 1980, cada fabricante de computador
tinha seu próprio formato para representar números em ponto
flutuante.
Solução: criação do Padrão 754 (IEEE 1985).
O Padrão IEEE 754 procurou uniformizar a maneira como as
diferentes máquinas representam os números em ponto
flutuante, bem como devem operá-los.
O padrão IEEE 754 para ponto (vírgula) flutuante é a
representação mais comum para números reais em
computadores de hoje, incluindo PC's compatíveis com Intel,
Macintosh, e a maioria das plataformas Unix/Linux.
•
•
•
•
Notação em Ponto
Flutuante
O padrão IEEE 754 define três formatos:
– Precisão simples (32 bits)
– Precisão dupla (64 bits)
– Precisão estendida (80 bits)
Notação em Ponto
Flutuante
•
Por que aumentar mais os bits de mantissa que os de
expoente?
Notação em Ponto
Flutuante
Exercícios
Exercícios
Exercícios
• 1. Represente o número 273,5234 segundo
padrão IEEE de 32 bits
• 2. Converta o número obtido acima para
decimal.
• 3. Escreva a palavra Abacaxi como o
computador a vê, isto é, usando os códigos
ASCII dos caracteres. Use a notação
hexadecimal
Exercícios
• 1. Efetue a soma computacional binaria 123 + (418).
– A) utilizando a representação MS
– B) utilizando a representação C1
– C) utilizando a representação C2
• Ao final converta os resultado para decimal.
Exercícios
(Questão 1 – Petrobrás – Analista de Sistemas
Júnior – Engenharia de Software – ano 2010)
Ao converter o número (1011100)2 da base binária
para as bases decimal, hexadecimal e octal,
obtêm-se, respectivamente, os valores:
a) 2910, B416 e 5608
b) 2910, 5C16 e 1348
c) 9210, B416 e 5608
d) 9210, 5C16 e 1348
e) 9210, 5C16 e 2708
Exercícios
(Questão 22 – BADESC – Análise de Sistemas – ano 2010)
O sistema binário representa a base para o funcionamento dos
computadores. Assim, um odômetro binário mostra no display o
número 10101111.
A representação desse número em decimal e em hexadecimal e
o próximo número binário mostrado no display, serão,
respectivamente:
a) 175, AE e 10101110
b) 175, EF e 10110000
c) 175, AF e 10110000
d) 191, EA e 10110000
e) 191, FA e 10101110
Exercícios
(Questão 34 – TRT – Analista Judiciário – Tecnologia da
Informação – ano 2011)
Considere o quadro abaixo:
Exercícios
(Questão 22 – Petrobrás – Analista de Sistemas Júnior –
Suporte de Infraestrutura – ano 2005)
Um computador utiliza representação de inteiros em
complemento a dois (C2) com valores armazenados em 8 bits.
Indique qual é a representação em C2 do valor decimal -123.
a) 10000101
b) 10000100
c) 01111011
1111011 Binário
d) 11111011
0000100 C1
e) 10000111
+
1
---------------------0000101 acrescentar o sinal
10000101
Exercícios
(Questão 31 –
CESGRANRIO - 2013 - BNDES - Profissional Básico - Análise d
– Desenvolvimento)
Muitas vezes é necessário converter a representação de um
número inteiro com n bits para sua representação com m bits,
onde m > n.
Se a representação em complemento de dois com 8 bits do
número inteiro positivo +19 é 00010011, a representação em
complemento de dois com 16 bits do número inteiro negativo
-19 é
a) 1000000000010011
b) 1000000011101101
c) 1000000010010011
d) 1111111111101101
e) 1111111100010011
Exercícios
(CESPE
- 2009 - ANAC - Analista Administrativo - Tecnologia da Inform
)
Considere que os números, em decimal, A = -345 e B = +239
sejam convertidos para a representação em complemento a 2,
usando-se registradores de 16 bits. Qual o resultado da
operação A – B, demonstre os cálculos.
1111110110111000.
OBRIGADO!