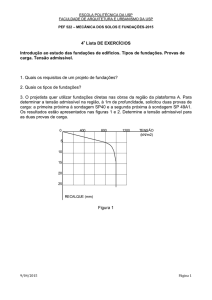
Geotecnia e Fundações, Arquitectura
Capítulo 2
CONCEITOS BÁSICOS DE MECÂNICA
Geotecnia e Fundações, Arquitectura
1. Noção de tensão e de deformação
Tensão:
F
σ=
A
σ - Tensão (N/m2 ou Pa)
F – força (N)
A – Área (m2)
Estado interno gerado num corpo para equilibrar
a força F aplicada numa dada área de contacto A
Deformação:
∆L
ε=
L0
F
Por exemplo, num
ensaio de um provete
de aço à tracção:
∆L
L0
1
Geotecnia e Fundações, Arquitectura
No espaço bidimensional
σy
y
σ xxσ xy
σ =
σ yxσ yy
τyx
τxy
σx
σ x σ x
σ = σ y = σ y
σ xy τ xy
σx
τxy
τyx
σy
x
σ xy = τ xy = σ yx = τ yx
Para os solos é costume adoptar-se
y=1(direcção vertical, do peso próprio)
x=2 (direcção horizontal)
Geotecnia e Fundações, Arquitectura
As deformações têm igual correspondência
σ
ε
τ
γ
Significado físico das deformações:
εyy
εxx
εyy
y
extensão
1/2γyx
1/2γ
1/2γxy
εxx
1/2γxy
1/2γ
γ
εxx
1/2γyx ε
yy
x
distorção
2
Geotecnia e Fundações, Arquitectura
Círculo de Mohr das tensões
Nos solos não há
valores negativos de
tensões normais
τ
σy
y
B
σx
τyx
90º
A
τxy
τyx
A
τxy
τxy
2x90º
σx
σx
σy
σy
τyx
x
σ
B
No espaço bidimensional
Convenção de sinais adoptada
na Mecânica dos Solos
σ xxσ xy
σ =
σ yxσ yy
Compressões
positivas
σ x σ x
σ = σ y = σ y
σ xy τ xy
Tensões tangenciais
positivas quando os
binários fazem rodar
no sentido anti-horário
+
Geotecnia e Fundações, Arquitectura
Círculo de Mohr
σV=σI
σH=σII
B
σH=σII
A
σA’
σB’ τB’
σV=σI
Cada ponto do círculo de
Mohr representa o estado
de tensão num plano com
uma dada orientação no
espaço 2D.
τA’
θ
A’
τA’
B’
σB’
τB’
σA’
As rotações dos planos, no círculo, são o
dobro das rotações reais (observadas no
espaço).
σI e σII são as
tensões principais
τ
τB’
O sentido é o mesmo porque a convenção de
sinais adoptada na mecânica dos solos para
as tensões normais é contrária à adoptada na τA’
Mecânica dos Meios Contínuos.
σH=σII
σA’
σB’
2xθ
σV=σI σ
3
Geotecnia e Fundações, Arquitectura
Círculo de Mohr das deformações
1/2
δεy
y
1/2
1/2
90º
A
δγxy
A
1/2δγyx
B
δεx
Pode haver valores
positivos e negativos
de deformações
volumétricas
δγ
1/2
1/2
δγxy
δγxy
2x90º
δεx
δεx
δγyx
δεy
1/2
δεy
δε
δγyx
B
x
No espaço bidimensional
ε x ε x
ε = ε y = ε y
ε xy 1 γ xy
2
1
δε xxδε xy δε xx 2 δγ xy
ε =
=
δε yxδε yy 1 δγ δε
2 yx yy
Convenção
de sinais igual
à das tensões
Geotecnia e Fundações, Arquitectura
2. Modelos de comportamento mais usuais
1- Elástico linear
1 − ν
ν
σ 11
E
1 −ν
σ 22 =
ν
σ (1 + ν )(1 − 2ν )
12
0
0
σ1
σ1=Eε1
E – módulo de
Elasticidade
ε11
0 ε 22
1 − 2ν ε12
2
0
Constantes elásticas:
E, v e G
ε3
ε1
σ1
ε1
ε3= -vε1
G=
E
2(1+v)
G –módulo de distorção
v – coeficiente de Poisson
4
Geotecnia e Fundações, Arquitectura
2- Elástico não linear
σ1
Etan – módulo de elasticidade
tangente
Esec – módulo de elasticidade
secante
ε1
Pequenas deformações
Pode ser assumido como um comportamento
elástico linear nas pequenas deformações
Geotecnia e Fundações, Arquitectura
3- Elástoplástico
σ
εP
de
sc
arg
rec
a
arg
a
ca
rga
Tensão de
σy
cedência
εe
ε
εP - Deformações irreversíveis ou plásticas
εe - Deformações elásticas ou reversíveis
5
Geotecnia e Fundações, Arquitectura
Para os materiais mais comuns em Engenharia Civil:
σ
Betão (compressão simples)
Aço (tracção)
σ
σ=Eε
E
σ=Eε
E
ε
ε
Elástico não linear
Elástico linear
Solo (compressão com tensões crescentes de confinamento)
σV
σH crescentes
σV
σH
σH
σV
E
ε
Elastoplástico
Geotecnia e Fundações, Arquitectura
3. Tensões nos solos
Superfície do terreno
Na ausência de carregamento,
num ponto à profundidade z, as tensões
são devidas ao peso do solo:
z
σV=σI
σH=σII
σH=σII
σV=σI
Tensões
verticais:
σV = γ h z
Tensões
horizontais:
σ H = kσ V = kγ h z
γh – peso volúmico do solo
(seco, húmido ou saturado)
k – coeficiente de impulso (há várias
expressões para o seu cálculo)
Convenciona-se que a direcção vertical
e a horizontal são direcções principais
6
Geotecnia e Fundações, Arquitectura
Tensão total, pressão intersticial e tensão efectiva
Solo
húmido
NF
Solo
saturado
(submerso)
z1
A
zA
Tensão total:
σA=γhzA
z2=hw
σB=γhz1+γsathw
B
A presença de água no solo
tem que ser considerada
Pressão intersticial:
uA=0
u=γwhw
uB=γwhw
com γw =10kN/m3
(peso volúmico da água)
Geotecnia e Fundações, Arquitectura
Pressão intersticial
Representações
mais usuais:
u<0
Solo
húmido
(Sr<100%)
N.F.
Solo
saturado
(Sr=100%)
N.A.
u>0
É positiva nos solos totalmente saturados e negativa
(sucção) caso os solos não estejam saturados.
7
Geotecnia e Fundações, Arquitectura
Pressão intersticial
É a pressão na água dos vazios do solo (solo
completamente saturado).
É isotrópica ou hidrostática (igual em todas as
direcções).
A resultante das pressões intersticiais é a
impulsão. Esta força opõe-se ao peso nos corpos
submersos.
Geotecnia e Fundações, Arquitectura
Tensão efectiva
NF
z1
A
zA
z2=hw
B
σ’ = σ - u
σ’v
σ’h
pressão intersticial:
tensão efectiva:
u
σv
σ’h σh
=
σ’v
σh
-
u
u
u
σv
tensão
=
efectiva
Tensão total:
Conceito de tensões
efectivas de Terzaghi
tensão
total
-
pressão
intersticial
σA=γhzA
uA=0
σB=γhz1+γsathw
σ’A=γhzA
σ’B=γhz1+(γsat-γw)hw
uB=γwhw
Peso volúmico submerso: γsub ou γ’
8
Geotecnia e Fundações, Arquitectura
Tensão efectiva (Cap. 4)
Sendo o solo um agregado de partículas sólidas,
a sua resistência e variação de volume depende
do arranjo das partículas (estrutura granular).
Ar (fase
gasosa)
Partícula
sólida
Vazio com ar
e água
Partícula
sólida
Água (fase
líquida)
Partícula
sólida
Menisco
Geotecnia e Fundações, Arquitectura
Tensão efectiva (Cap. 4)
No caso dos solos não
estarem saturados, há
água a formar meniscos
nos contactos entre as
partículas. Do equilíbrio
entre a pressão do ar e da
água existentes nos vazios
surgem forças de
capilaridade (T) .
menisco
Tubo capilar com
diâmetro d
hc - altura da
água no tubo
capilar
As forças capilares unem as partículas entre si e, deste modo,
aumentam a resistência do solo. Anulam-se quando o solo é
completamente saturado, o que explica a perda significativa
de resistência observada, por exemplo, na areia húmida.
9
Geotecnia e Fundações, Arquitectura
Tensão efectiva (Cap. 4)
Do ponto de vista macroscópico, o solo
entende-se como um meio contínuo e o
seu comportamento, descontando a
presença da água, explica-se por variações
de tensões efectivas
Verifica-se experimentalmente que
as tensões efectivas são as
responsáveis pelas variações de
volume e pela resistência dos solos.
Geotecnia e Fundações, Arquitectura
Exemplo de Aplicação
Para os pontos A e B:
a) Calcule a tensão total, σ.
b) Calcule a pressão intersticial, u.
c) Calcule a tensão efectiva, σ’.
N.F.
0,0 m
σA=120kPa
σB=200kPa
uA=60kPa
uB=100kPa
σ’A=60kPa
σ’B=100kPa
Areia:
γsat=20kN/m 3
A
B
6,0 m
10,0 m
10
Geotecnia e Fundações, Arquitectura
Capítulo 3
COMPORTAMENTO FRICCIONAL
E COESIVO
Geotecnia e Fundações, Arquitectura
1. Resistência ao corte
- Distorção de um corpo e rotura por corte
F
F
F
Plan
o de
τ
γ
Distorção
corte
σ
Rotura por corte
(Comportamento (Comportamento
elástico)
plástico)
A tensão neste plano
é independente da
deformação
τ= f(σ)
11
Geotecnia e Fundações, Arquitectura
- Critério de rotura de Mohr-Coulomb
Comportamento friccional
τ
τ
+
= c’
σ- tensão normal
τ- tensão tangencial
µσ’
φ’
µ - coeficiente de atrito
T
c’
Fa=µP
σ’
P
em equilíbrio, T=Fa
τ = c’ + σ’ tanφ’
σ’ – tensão efectiva (normal ao plano de corte)
c’ – coesão (MPa) (c’=0 se material tem comport. friccional)
φ’ – ângulo de resistência ao corte
Geotecnia e Fundações, Arquitectura
se c’=0
Demonstra-se que, na rotura, a relação
entre as tensões principais do círculo
de Mohr é dada pela expressão:
σ 'II
σ 'I
τ
C
=
1 − sin φ '
1 + sin φ '
φ’
τRotura
A
σ’II
90º-φ
φ’
B
σ’I
σ’
A e B – planos
principais
C – plano de
rotura
12
Geotecnia e Fundações, Arquitectura
- Critério de rotura de Tresca
τ- tensão tangencial
τ
Cu
τ = Cu
Cu – resistência não drenada
(coesão não drenada)
T
σ
F=Cu
Comportamento coesivo (solos coerentes)
τ = Cu
A resistência ao corte resulta das
ligações internas do material
Geotecnia e Fundações, Arquitectura
2. Comportamento friccional
τ = c’ + σ’ tanφ’
Verifica-se nos materiais granulares
Se c=0, o material tem
comportamento puramente
friccional (é o caso das areias)
τ
σ’
c=0, a envolvente
passa na origem
Escreve-se em termos de tensões efectivas
porque se tem que se descontar a parcela do
carregamento (peso) equilibrada pela pressão
intersticial
Corresponde a uma resposta em condições drenadas
13
Geotecnia e Fundações, Arquitectura
3. Comportamento puramente coesivo τ = cu
Verifica-se nos materiais coerentes como é o caso
das argilas e de solos com uma percentagem
importante de argila
Escreve-se em termos de tensões totais porque
não depende do nível de tensão instalado
(devido ao carregamento ou ao peso, por
exemplo)
Corresponde a uma resposta em condições não
drenadas
Geotecnia e Fundações, Arquitectura
4. Propriedades de resistência (Cap. 4)
As propriedades de resistência (φ’, c’ e Cu) são obtidas
em ensaios realizados para medir a resistência ao
corte de solos
Caixa de corte
Alguns ensaios
mais correntes:
Corte simples
Ensaio Triaxial
Verdadeiro ensaio triaxial
No ensaio aplicam-se forças (tensões) que provocam a
rotura por corte (há corte porque há distorção).
Durante o ensaio medem-se as tensões e as
deformações até à rotura.
14
Geotecnia e Fundações, Arquitectura
Ensaio mais simples: Caixa de corte
N
σxx
δx
T
τyx
δy
y
γyx
x
Caixa de corte
Caixa de corte
N
Ω
T
=
Ω
τ
σ xx =
τ xy
Ω - área de contacto
(ou da superfície
onde ocorre a rotura
por corte)
Ponto na
envolvente
de rotura
τyx
σxx
σ
Geotecnia e Fundações, Arquitectura
τzx
τpico
Explicação física:
F
Areia densa
h1
τresidual
Areia solta
δVolume
h2
h2>h1
γzx
Aumento de
volume
Areia densa
ψ>0 (dilatante: aumento de volume)
γzx
ψ<0 (contráctil: diminuição de volume)
Areia solta
15