Lista de exercícios – Resistência Elétrica - EaD

Lista de exercícios – Resistência Elétrica
Resistividade e Resistência:
Apesar do condutor possuir elétrons livres, as cargas não são totalmente livres
para se mover. O movimento das cargas depende de propriedade do material e do
campo elétrico aplicado. Para a maioria dos metais, a uma dada temperatura, a
densidade de corrente é quase diretamente proporcional ao campo elétrico
aplicado. Esta relação recebe o nome de lei de Ohm
=
E – campo elétrico
J – densidade de corrente
ρ – resistividade do material
Quanto maior a resistividade de um material maior deve ser o valor do campo E
para se produzir a mesma densidade de corrente (é mais difícil a carga se mover!).
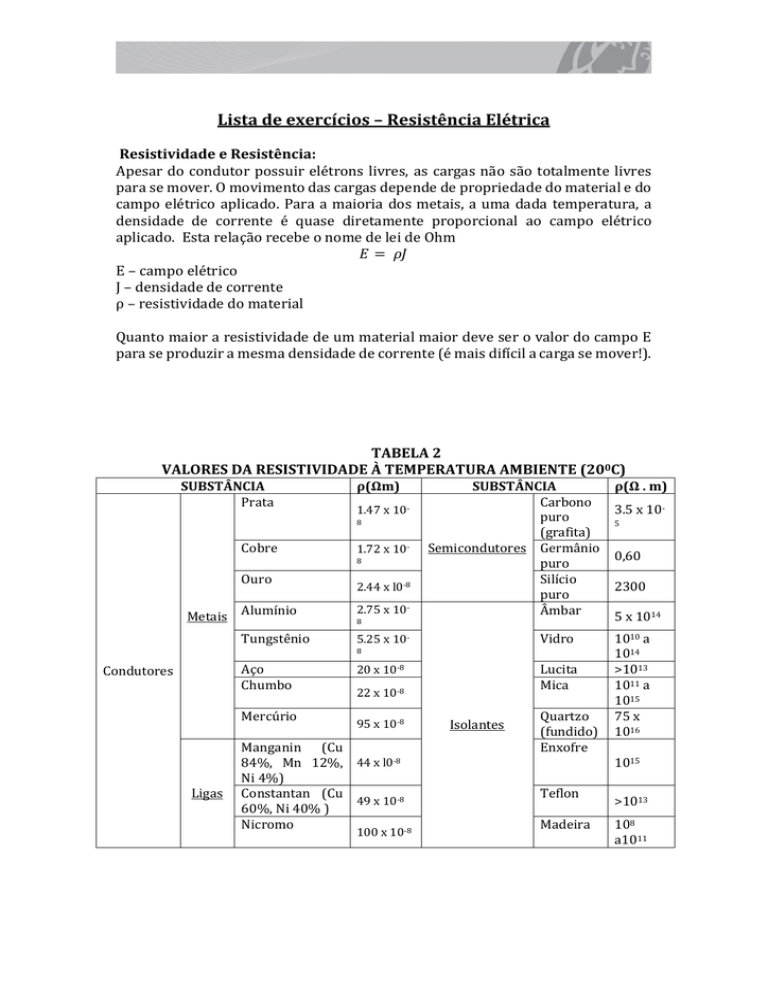
TABELA 2
VALORES DA RESISTIVIDADE À TEMPERATURA AMBIENTE (200C)
SUBSTÂNCIA
Prata
ρ(Ωm)
1.47 x 108
Cobre
1.72 x 108
Ouro
Metais Alumínio
Tungstênio
2.44 x l0-8
2.75 x 10-
SUBSTÂNCIA
Carbono
puro
(grafita)
Semicondutores Germânio
puro
Silício
puro
Âmbar
8
Vidro
5.25 x 108
Aço
Chumbo
Condutores
Mercúrio
Ligas
Lucita
Mica
20 x 10-8
22 x 10-8
95 x 10-8
Manganin (Cu
84%, Mn 12%, 44 x l0-8
Ni 4%)
Constantan (Cu
49 x 10-8
60%, Ni 40% )
Nicromo
-8
100 x 10
Isolantes
Quartzo
(fundido)
Enxofre
ρ(Ω . m)
3.5 x 105
0,60
2300
5 x 1014
1010 a
1014
>1013
1011 a
1015
75 x
1016
1015
Teflon
Madeira
>1013
108
a1011
Para ir de um ponto a até um ponto b de um condutor, os elétrons perdem energia
(existe um diferença de potencial entre estes pontos). Esta ddp é denominada
também de tensão elétrica (V) e se relaciona com corrente pela equação
=
V – tensão entre dois pontos de um condutor (volts)
I – corrente elétrica (ampère)
R – resistência elétrica (ohms, Ω)
Pense e Responda: Usando as equações da lei de Ohm ( = ), densidade de
corrente (J = I/A) e da diferença de potencial entre as extremidade de um condutor
(E = VL), mostre que a resistência de um condutor é dada por
=
R – resistência elétrica (Ω)
ρ – resistividade elétrica (Ωm)
L – comprimento do condutor (m)
A – área de seção reta (m2)
Exercícios:
1. Nas instalações elétricas de uma casa, geralmente se usa um fio de cobre com
diâmetro de 2,05 mm. Calcule a resistência de um fio de cobre com comprimento
igual a 24,0 m. 1,24 x 10-1 Ω
2. Um fio de comprimento L = 1,70 m e área da seção reta A = 1,80 x 10-6 m2 tem
uma resistência R = 6,46 x 10-2 Ω. Determine a resistividade do material que
compõe o fio. 6,84 x 10-8 Ω.m
3. Que diâmetro deve ter um fio de cobre para que sua resistência seja a mesma
que a de um fio de alumínio com mesmo comprimento e com diâmetro igual a 3,26
mm? 2,58 x 10-3 m
4. Como parte de uma aula experimental, uma professora de física planeja prender
com as mãos dois pontos de um fio desencapado conduzindo uma corrente
elétrica. Por motivo de segurança, a diferença de potencial entre suas mãos não
deve ser maior do que 1,50 V. A distância entre suas mãos é igual a 1,2 m e ela
segura firmemente os dois pontos do fio. O fio é feito de alumínio e deve conduzir
uma corrente de 6,00 A. Qual é o raio mínimo do fio consistente com a diferença
de potencial de segurança? 2,05 x 10-4 m
5. Você aplica uma diferença de potencial de 4,50 V entre as extremidades de um
fio de 2,50 m de comprimento e raio igual a 0,654 mm. A corrente resultante é
igual a 17,6 A. Qual e a resistividade do fio? 1,37 x 10-7 Ω.m
6. Um fio de comprimento L e seção reta com área A possui uma resistência R.
Calcule a resistência do fio supondo que ele seja esticado até o dobro de seu
comprimento original. Suponha que a resistividade do material e a sua densidade
não sejam alteradas quando este é esticado.
4R
7. Um pedaço de fio possui resistência igual a 5,60μΩ. Calcule a resistência de um
resistor formado por 120 fios iguais a esse quando eles são montados: a) lado a
lado formando um cabo com o mesmo comprimento do pedaço de fio considerado;
b) conectados pelas extremidades formando um fio com um comprimento 120
vezes maior do que o do pedaço de fio inicial.
a) R = 4,67 x 10-8 Ω
b) R = 6,72 x 10-4 Ω