Simulação

Universidade de Coimbra
Faculdade de Ciências e Tecnologia
Eng.ª Biomédica
Modelos dos Processos Fisiológicos no Homem
Trabalho elaborado por:
[email protected]
Carla Pereira
Edite Figueiras
Lara Aires
Narciso Beça
INTRODUÇÃO
No âmbito do programa da disciplina de Modelos dos processos fisiológicos no
Homem que visa o estudo da modelização de sistemas biológicos, processo este que é
cada vez mais importante, uma vez que permite caracterizar o comportamento e
evolução dos mesmos sem métodos “invasivos”. Assim sendo, as simulações
desempenham um papel preponderante uma vez que permitem variações nas condições
dos sistemas e dos respectivos meios ambientes, bem como das suas propriedades
intrínsecas sem implicar consequências nefastas para o organismo modelizado. A
simulação representa assim um método seguro, eficaz e fiável de estudar e prever o
comportamento dos organismos vivos. Durante algum tempo o modo como uma célula
é excitada era uma incerteza que persistia mas que foi clarificada com base nos
trabalhos realizados por Hodgkin e Huxley.
O nosso estudo consistiu em interpretar o modelo proposto por Hodgkin e
Huxley que explica como evolui o potencial de acção membranar e implementá-lo em
Simulink.
2
Nos trabalhos realizados por Hodgkin e Huxley foi utilizado o neurónio da lula
para fazer estudos sobre o potencial de acção pois o diâmetro do seu axónio permite a
inserção de eléctrodos axiais. Colocando outro eléctrodo num fluido fora do axónio a
diferença de potencial através da membrana pode ser medida.
Também se pode estimular este axónio injectando corrente com eléctrodos extra
celulares produzindo uma potencial de acção que se propaga ao longo do axónio. Este
potencial de acção pode ser registado por um eléctrodo intracelular.
Os neurónios dos mamíferos são muito pequenos, por isso, não é possível realizar esta
experiência com estes neurónios.
Todas as células vivas apresentam um gradiente eléctrico através das suas
membranas, mas o sistema nervoso, constituído por neurónios, é o que faz o mais
sofisticado uso dos potenciais da membrana. O sistema nervoso dirige e regula
processos corporais usando como meio de transmissão de informação os potenciais
eléctricos. Estes sinais eléctricos são originados pelo impulso nervoso, uma onda móvel
de alterações químicas e eléctricas que afecta a membrana da célula nervosa e envolve
alterações sequenciais na permeabilidade do neurónio aos iões de sódio e de potássio.
Os neurónios são constituídos pelo corpo celular, dendrite e o axónio. Os
impulsos são recebidos pelo corpo celular e passam, como uma pulsão de corrente
eléctrica, ao longo do axónio, a qual termina na sinapse, área especializada e muito
ligada à célula seguinte que pode ser outro neurónio ou outra célula. Ao atingir a
sinapse, o impulso liberta uma substância química, neurotransmissores, que se difundem
à célula vizinha, estimulando aí outro impulso.
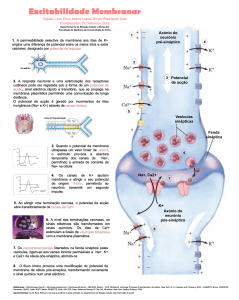
A transmissão do impulso nervoso é apresentada na figura seguinte.
3
A transmissão do impulso nervoso envolve a abertura e o encerramento de certos
canais selectivos existentes na membrana celular, para permitir que determinados iões
entrem ou saiam da célula.
A fibra nervosa em repouso tem uma carga negativa líquida, porque há mais iões
+
de Na no exterior do axónio do que no interior. Esta diferença de potencial mantém-se
graças a uma bomba química que envia esses iões de Na+ para fora e os de K+ para
dentro. Estes também deixam o axónio por difusão, através dos poros da membrana (1).
4
A chegada do impulso nervoso abre as portas dos Na+, que entram no axónio,
tornando-o positivo (despolarizado) (2).
Em seguida, essas portas fecham-se e a bomba Na+/K+ restabelece a pouco e
pouco o potencial de repouso (3). O impulso passa à célula seguinte através da sinapse
(4).
Os axónios são os elementos neuronais especificamente preparados para a
transmissão de potenciais de acção, funcionando como um cabo condutor que transmite
impulsos.
Uma diferença de potencial aplicada através de uma membrana neuronal não
consegue percorrer um milímetro sem sofrer distorções devido às propriedades
capacitivas da membrana e devido à diminuição de amplitude que resulta da perda de
corrente através da membrana. A capacitância (Cm) e resistência (Rm) são dois factores
determinantes das propriedades axoniais. O axónio compensa ao incrementar o seu sinal
ao longo de todo o percurso, regenerando continuamente o potencial de acção. Desde
que um estímulo, num dos lados, produza uma corrente de despolarização
suficientemente intensa para elevar a membrana circundante até ao limiar da
despolarização, fica assegurado que o impulso seja transmitido até a extremidade do
axónio.
5
POTENCIAL DE NERNST
Como já foi referido, a concentração de K+ é maior dentro do axónio, enquanto
que o Na+ esta mais concentrado fora deste. Este gradiente de concentração é mantido
devido à bomba Na+/K+. Como consequência, o potencial desta célula é negativo. O K+
vai difundir-se segundo o seu gradiente de concentração, isto é, para fora do axónio,
criando excesso de carga positiva fora do neurónio. Esta carga impede a difusão
continuada do K+ para o fluido extracelular. Atinge-se assim um ponto de equilíbrio em
que a diferença de potencial através da membrana suficientemente forte para impedir o
fluxo de K+ para o exterior do neurónio. A diferença de potencial resultante do ponto de
equilíbrio pode ser directamente calculada a partir da relação da concentração do ião
móvel, dentro e fora do neurónio, aplicando a equação de Nernst. O potencial de
equilíbrio do ião K+ é:
§ >K @e ·
RT
¸¸
EK
log¨¨
F
© >K @i ¹
R: constante dos gases
T: temperatura absoluta
F: carga por mole de ião univalente
6
MEMBRANA LINEAR
Considera-se a membrana celular constituída por uma bicamada lipídica, com
elevada resistência, e por canais de potássio. A corrente através dos poros é dada por:
IK=gK(V-EK) (1)
Figura: Circuito equivalente à fórmula
A corrente será igual a zero se o potencial transmembranar está ao potencial de
Nernst; a corrente entrará na célula se o potencial transmembranar for negativo
relativamente ao potencial de Nernst e sairá caso contrário.
Quando o potencial da membrana não esta num valor de equilíbrio, isto é, quando a
potencial é alterada haverá corrente através do condensador. A capacitância é devida ao
facto da membrana ser isoladora e estar rodeada em ambos os lados por um fluido
condutor.
A equação do condensador é:
Q = -CV
Q: carga do condensador
C: capacitância
7
V: potencial nos terminais do condensador
Diferenciando a equação:
dV
dt
IK
C
gK
V EK V EK (2)
C
W
Com:
C
gK
dQ
I=
dt
IJ=
IJ: constante temporal
A solução da equação diferencial (2) é:
V(t) = EK-(EK-V(0))e-t\ IJ (3)
Na realidade, a corrente de potássio não é dada pela equação (1), pois foi
assumido que a probabilidade do canal estar aberto é constante, independente do tempo
e da potencial (gk não é função do tempo e da voltagem), o que não acontece.
8
VOLTAGE-CLAMPING
Esta técnica envolve a introdução de dois eléctrodos internos: um para medir o
potencial transmembranar, e outro para injectar corrente.
Usando um circuito electrónico de feedback, um determinado potencial é
mantido através da membrana. A corrente injectada pelo circuito é o reflexo da corrente
na membrana àquele potencial. O tamanho da preparação é suficientemente curto para
que os efeitos da velocidade da corrente intracelular sejam desprezados.
A corrente resultante de um degrau voltage-clamp desde -65mV ate -9Mv é a
soma de quatro diferentes correntes:
9
Corrente capacitiva, corrente leakage, corrente de sódio e corrente de potássio.
A corrente de potássio activa-se lentamente, mas não fica inactiva.
A corrente de sódio activa-se rapidamente, mas depois torna-se inactiva, apesar
do potencial se manter constante.
10
FORMALISMO DE HODGKIN-HUXLEY
O modelo de Hodgkin-Huxley para o axónio da lula é um sistema de equações
diferenciais a quatro dimensões que descreve as três correntes responsáveis pelo
potencial de acção nestes neurónios. A corrente de sódio (INa) é responsável por gerar o
pico do potencial de acção, a corrente de potássio (IK) repolariza a membrana. A
corrente leakage (IL) é muito menor do que as outras duas.
No entanto outros neurónios podem ter outras correntes que não são
consideradas neste modelo.
Fizeram-se vários registos da corrente de K+ através de um poro quando o
potencial varia de -100mV até 50mV:
De onde resulta a seguinte curva, que representa uma média dos registos obtidos
para a corrente de K+:
11
Considera-se que existe apenas um poro por onde passa a corrente de K+, que
segue um esquema reaccional de primeira ordem :
Įn e ȕn são constantes de velocidade em função do potencial. Estas constantes controlam
a transição entre o canal fechado (C) e o canal aberto. A variável n é a fracção de poros
que estão abertos. Então:
nf n
dn
(4)
D n (1 n) E n n
Wn
dt
Onde:
nf
Wn
Dn
D n En
1
Dn En
As curvas de n’ e IJn evoluem em função do potencial.
A solução da equação diferencial (4) quando V é constante é:
n(t)
n f - (n f - n(0))e-t/W n
(5)
Então a fórmula para a corrente será:
Ik = g K n (V-EK) (6)
12
g K : máxima condutância
Mas a figura seguinte mostra que gk tem forma de onda, não sendo uma simples
exponencial.
Então, Hodgkin e Huxley elevaram n a potência 4, resultando:
I K (V, t)
g K (V - E K )
g K [n(V, t)]4 (V - E K ) (7)
A evolução de n e n4 em função do tempo. Como se pode verificar, a curva n4
mostra correctamente a evolução da corrente de potássio.
13
Fizeram-se vários registos da corrente de Na+ através de um poro quando o
potencial varia de -80mV até -40mV:
De onde resulta a seguinte curva, que representa uma média dos registos obtidos
para a corrente de Na+:
A equação desenvolvida por Hodgkin e Huxley para descrever a corrente de Na+
(INa), é:
I Na (V, t) g Na m 3 h(V - E Na ) g Na (V - E Na ) (8)
14
m: variável de activação
h: variável de inactivação
Nela está implícito que:
gNa(V,t) = g Na [m(V, t)]3 h(V, t) =
I Na (V , t )
(9)
(V E Na )
A figura seguinte representa esta equação:
As equações que reflectem o movimento no canal m são semelhantes às do canal
n. Assumindo novamente um esquema cinético de primeira ordem:
Įm e ȕm são constantes em função do potencial. A variável m satisfaz:
dm
dt
D m (1 m) E m m
mf m
Wm
(11)
Onde:
mf
Dm
Dm Em
15
Wm
1
Dm Em
A solução da equação diferencial (11) quando V é constante é:
m f - (m f - m(0))e-t/W m (12)
m(t)
Para o poro h:
Įh e ȕh são constantes em função do potencial. A variável h satisfaz:
dh
dt
D h (1 h) E h h
hf h
Wh
(13)
Onde:
hf
Wh
Dh
Dh Eh
1
D h Eh
A solução da equação diferencial (13) quando V é constante é:
h(t)
h f - (h f - h(0))e-t/W h (14)
A fórmula geral para INa é:
I Na
g Na m 3 h(V - E Na )
Em que m satisfaz a equação (11) e h satisfaz a equação (13).
16
Quando m’,IJm, h’ e IJh em função do potencial.
A evolução de m m3 e m3*h em função do tempo
17
Então o sistema de quatro equações não lineares que irão ser usadas no
MatLab/Simulink é:
x
x
x
x
mf m
dm
D m (1 m) E m m
dt
Wm
hf h
dh
D h (1 h) E h h
Wh
dt
nf n
dn
D n (1 n) E n n
dt
Wn
dV
1
[ g Na m 3 h(V E Na ) g K n 4 (V E K ) g L (V E L ) I stim ]
dt
C
Onde:
120 mScm 2
x
g Na
x
x
x
x
x
x
x
g K 36 mScm 2
g L 0.3 mScm 2
ENa = +55 mV
EK = - 72 mV
EL = -49.387 mV
C = 1 µFcm-2
Istim correntes de estímulos
As constantes dependentes do potencial são dadas por:
x
x
x
x
x
x
Įm = 0.1 (V+35)/(1-exp(-(V+35)/10))
ȕm = 4 exp(-(V+60)/18)
Įh = 0.07 exp(-(V+60)/20)
ȕh = 1/(exp(-(V+30)/10)+1)
Įn = 0.01(V+50)/(1-exp(-(V+50)/10))
ȕn = 0.125 exp(-(V+60)/80)
Reunindo todas as equações anteriores, produz-se um modelo de implementação
em Matlab e outro em Simulink, que se encontram anexados.
18
Gráfico resultante do MatLab
1º gráfico
Azul – dV/dt
2º gráfico
Azul – dm/dt
Vermelho – dn/dt
Verde – dh/dt
19
Gráfico resultante do Simulink
1º gráfico
Azul – dV/dt
Verde – I stim
2º gráfico
Azul – dh/dt
Vermelho – dn/dt
Verde – dm/dt
20
Verifica-se que os resultados das simulações realizadas são bastante semelhantes
aos obtidos por Hodgkin e Huxley. Há a ter em conta que se nota um ligeiro
desfasamento, devido ao facto de a implementação do impulso na simulação ser
realizado na primeira unidade de tempo e não na quinta, como no modelo experimental.
21
CONCLUSÃO
Com este trabalho tivemos oportunidade de conhecer o Modelo proposto por
Hodgkin e Huxley e confirmar os resultados por eles obtidos. Deve ter-se em atenção
que este modelo contempla apenas três correntes iónicas, sendo que existem células
com mais.
A sua implementação em Simulink é bastante complexa, devido ao elevado
número de constantes e equações diferenciais. Contudo a sua implementação em Matlab
torna-se acessível pois trata-se de equações diferenciais de primeira ordem, as quais são
facilmente definidas pela função Ode. Em ambos os casos, os resultados obtidos são
concretos e fiáveis.
Tratando as informações obtidas nas simulações, pode prever-se como evolui o
potencial de acção membranar e concluir como decorre o processo de excitação na
célula.
22
BIBLIOGRAFIA
Manual cedido pelo docente.
23