Março – Matemática II – 1ª Série

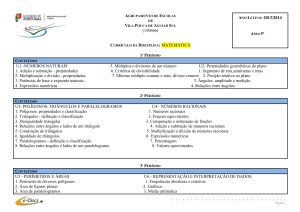
Março – Matemática II – 1ª Série
Semelhança de triângulos sempre é assunto cobrado nos principais vestibulares do país.
Dominar este tópico garante a compreensão de boa parte do entendimento da geometria
plana.
Algumas dicas:
Depois de garantido que os triângulos são semelhantes (dois ângulos de medidas
congruentes)


Localize inicialmente os lados correspondentes. Use a oposição aos ângulos para
isso ou, se preferir coloque os triângulos em posições iguais.
Escolha a ordem de montagem das razões (do maior para o menor ou do menor
para o maior)
Exercícios resolvidos:
01. Os triângulos ABC e AED, representados na figura a seguir, são
semelhantes, sendo o ângulo ADˆ E é congruente ao ângulo ACˆ B .
Se BC = 16 cm, AC = 20 cm, AD = 10 cm e AE = 10,4 cm, o perímetro do quadrilátero BCED, em centímetros, é?
02. Na figura, sabe-se que Ŝ e B̂ são congruentes, AR = 7cm, AS = 5 cm, SR = 4
cm e AB = 10 cm. Determine AD = x e BD = y
03. A figura abaixo mostra um quadrado inscrito num triângulo de base 10
cm e altura 6 cm. Obter o perímetro do quadrado.
1
Resolução:
01. Os triângulos ADE e ABC são semelhantes, pois, têm dois ângulos congruentes: ( Cˆ  Dˆ e    ).
Separando os triângulos temos:
16 20

x 10
16 2

x 1
2 x  16
x8
20
y

10 10, 4
2
y
O perímetro do quadrilátero BCED é: 10,8+8+9,6+16 = 44,4 cm

1 10, 4
y  20,8
ˆ A
ˆ ).
02. Os triângulos ABD e ASR são semelhantes, pois, têm dois ângulos congruentes: ( Bˆ  Sˆ e A
Separando os triângulos temos:
10 x

5 7
5 x  70
x  14
10 y

5 4
5 y  40
y 8
ˆ e Eˆ  Cˆ ).
03. Os triângulos ABD e ASR são semelhantes, pois, têm dois ângulos congruentes: ( Bˆ  D
Separando os triângulos temos:
10
6

x 6 x
6 x  10(6  x)
Perímetro do quadrado é 4x3,75 = 15 cm
2
6 x  60  10 x
16 x  60
x  3, 75