XVII IMEKO World Congress

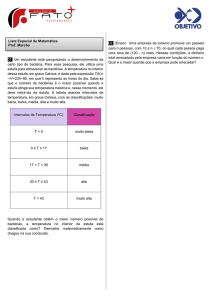
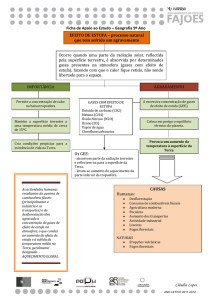
http://dx.doi.org/10.5540/DINCON.2011.001.1.0066
259
INFLUÊNCIA DOS GASES ESTUFA NA DINÂMICA DO MODELO DAISYWORLD
Flavio Maggessi Viola 1, Marcelo Amorim Savi 2
1
2
Universidade Federal do Rio de Janeiro - COPPE – Departmento de Engenharia Mecânica, Rio de Janeiro, Brasil, [email protected]
Universidade Federal do Rio de Janeiro - COPPE – Departmento de Engenharia Mecânica, Rio de Janeiro, Brasil, [email protected]
Resumo: Este trabalho discute a modelagem matemática do
aquecimento global, baseada no modelo Daisyworld que
representa a regulação planetária através da interação entre a
vida (populações de margaridas) e o ambiente (temperatura).
O modelo proposto incorpora uma variável relacionada aos
gases estufa. Simulações numéricas mostram diferentes
cenários associados ao aquecimento global.
Palavras-Chave: Daisyworld,
dinâmica de biossistemas.
aquecimento
global,
1. INTRODUÇÃO
Com o objetivo de representar o equilíbrio de um
sistema climático, [1-3] descrevem o modelo Daisyworld
(planeta das margaridas) para demonstrar que a regulação
global do planeta pode ocorrer pela interação entre a vida e
o ambiente. Daisyworld é um planeta imaginário semelhante
ao planeta Terra, iluminado por um sol que aumenta a sua
produção de calor à medida que envelhece. Sua atmosfera é
transparente, não possui nuvens e também não existem gases
estufa, com toda sua superfície fértil e poucos oceanos [4].
Sua população é composta de margaridas de diversas cores,
e em um caso particular, brancas e pretas. Este modelo
surgiu para testar a Teoria de Gaia que descreve que o
sistema planetário se auto-regula pela interação da vida
(populações) e o ambiente (temperatura).
A primeira menção sobre Gaia ocorreu em um artigo
publicado pelo cientista britânico James Lovelock, em 1972.
Em 1983, foi desenvolvido o modelo original do Daisyworld
apresentando as equações que governam o sistema [5]. Mais
tarde, [4] propôs a existência de populações de margaridas
de outras cores além das pretas e brancas do seu modelo
original.
Em [6] foram estudados os efeitos da evolução
adaptativa do Daisyworld permitindo que as margaridas
tivessem sua temperatura ótima de crescimento deslocada
eliminando a capacidade homeostática do Daisyworld.
Restrições nas condições ambientais foram propostas em
[7]. Posteriormente, esses dois trabalhos foram consolidados
em [8]. Através da introdução de uma fonte extra de
competição às equações que descrevem a interação entre as
espécies de margaridas, tenta-se constatar que a temperatura
do planeta estará ainda numa faixa adequada para a vida [9].
Daisyworld foi também estudado segundo um modelo
bidimensional com a introdução de uma curvatura na
superfície buscando analisar o efeito na interação do meio
ambiente caso houvesse a ocorrência de uma catástrofe [10].
Com base no modelo zero dimensional proposto em 1983
por James Lovelock, foi estudado um modelo
unidimensional incorporando-se uma distribuição da
radiação solar recebida e uma difusão de calor consistente
com um planeta esférico [11]. Em [12] apresentou uma
revisão geral da literatura associada ao Daisyworld,
enfatizando suas principais características e suas diferentes
abordagens para a análise, relatando a capacidade de
descrever tanto os fenômenos locais quanto globais [13,14].
O fenômeno do aquecimento global pode ser investigado
através de uma perspectiva dinâmica considerando duas
abordagens: análise de séries temporais de temperatura [15]
e modelagem matemática [16-17]. O modelo Daisyworld
pode incorporar uma variável relacionada aos gases de
efeito estufa possibilitando a análise do aquecimento global
[16]. Em [17] considera-se a evolução do transiente de
temperatura e a variabilidade climática considerando uma
variação senoidal da luminosidade solar.
Uma questão importante relacionada ao aquecimento
global é a preocupação com a sua reversibilidade. Em outras
palavras, é importante saber se a redução das emissões dos
gases estufa é suficiente para fazer a temperatura do planeta,
retornar a valores do passado. Neste trabalho, apresentam-se
simulações numéricas que representam diferentes cenários
da concentração dos gases estufa analisando o
comportamento com o modelo proposto.
2. O MODELO MATEMÁTICO
O primeiro passo da modelagem é a definição da vida,
representada pelas margaridas, cuja evolução é descrita pela
equação geral a seguir, onde i (i  1,2,...N ) representa a
área coberta pela população das diferentes margaridas:
(1)
o ponto sobre a variável representa a derivada no tempo,
é a variável da taxa de crescimento dependente
da temperatura,  é um parâmetro que representa a taxa de
mortalidade e é a fração de área descoberta do planeta.
As cores das margaridas definem a quantidade de
absorção de energia e o equilíbrio entre as populações de
margaridas pode controlar a temperatura do planeta. Uma
260
Influência dos gases estufa na dinâmica do modelo Daisyworld
Flavio Maggessi Viola, Marcelo Amorim Savi.
primeira abordagem a este modelo arquétipo é considerar
apenas duas populações de margaridas: pretas, αb e brancas,
αw. As Margaridas pretas absorvem mais energia, enquanto
margaridas brancas absorvem menos energia.
Com a finalidade de incorporar os gases estufa no
Daisyworld, uma nova população é incluída na modelagem.
A idéia é representar o aumento do albedo devido ao efeito
desses gases, representados pela variável G. Nesse contexto,
à inclusão do efeito estufa, variável G, tem um efeito
semelhante às margaridas pretas. Portanto, o modelo
proposto é escrito como no modo clássico, mas agora existe
uma função que estabelece o histórico de gases de efeito
estufa:
(2)
A variável
é a fração de área descoberta do planeta
representada por:
temperatura média global, aproximando-se um pouco mais
da situação real.
(8)
onde L (adimensional) é a luminosidade solar e S é a
constante solar que estabelece a energia solar média, SL; σ é
a constante de Stefan-Boltzmann, baseada na lei de StefanBoltzmann, que permite calcular a quantidade de radiação
emitida a partir da temperatura do corpo negro [22],
éa
derivada da temperatura no tempo e c é uma medida da
capacidade térmica média ou inércia térmica do planeta.
Uma das principais diferenças entre as mudanças
climáticas e a variabilidade climática é a persistência de
condições anômalas. Para investigar o efeito da
variabilidade climática no Daisyworld, assume-se que a
luminosidade solar apresenta uma variação senoidal
representada a seguir:
(9)
(3)
Aqui, p representa a proporção de terra disponível para o
crescimento das margaridas e N representa a biodiversidade
relativa ao número de populações envolvidas no sistema.
O albedo planetário médio do Daisyworld, A
(adimensional), pode ser estimado a partir do albedo
individual de cada população ( para as margaridas,
para a terra nua e G para os gases de efeito estufa) por:
Observe, que
podendo descrever um
crescimento linear, por exemplo, e o termo
representa uma perturbação que pode ser associada com a
variabilidade climática.
A forma da função  i é geralmente considerada como
uma função simétrica tipo sino, que representa a taxa de
crescimento das populações de margaridas, em função da
temperatura local Ti:
(4)
As temperaturas locais de cada população e a
temperatura da terra descoberta são dadas através de
aproximações em transferência de calor [18,19]. A equação
fornece o grau de conexão entre os conjuntos de margaridas
e independe da introdução de um espaço explícito. As
temperaturas locais das margaridas, da área descoberta do
planeta e dos gases, respectivamente,
e
são,
portanto, definidas como segue:
(5)
(6)
(7)
onde T é a temperatura média global do Daisyworld, e q é
uma constante usada para calcular a temperatura local em
função do albedo (uma medida do grau de isolamento entre
as regiões da superfície do planeta [20]), que é equivalente a
q’ = 20 utilizado em [5]. A equação diferencial
implementada em [21] é utilizada, Equação 8. Assim, o
modelo passa a apresentar características oscilatórias tanto
no comportamento das populações de margaridas quanto na
(10)
onde Topt é a temperatura ótima, geralmente assumida como
Topt = 295,5 °K = 22,5 °C. O parâmetro k representa o
tamanho da parábola, sendo definido a fim de estabelecer as
condições favoráveis à vida das populações, por exemplo,
entre 5°C e 40°C, k=17,5. Para temperaturas abaixo de 5°C
e acima de 40°C a taxa de crescimento é zero e para a
temperatura 22,5 °C a taxa de crescimento é máxima [5])
Do mesmo modo, B altera estes valores de forma a
representar diferentes características ambientais. O modelo
original considera que o valor de B é constante e igual a 1.
3. SIMULAÇÕES NUMÉRICAS
Para a simulação numérica do modelo Daisyworld
aplica-se o método de integração Runge-Kutta de quarta
ordem. Um estudo de convergência é feito comparando a
diferença nos resultados simulados com diferentes passos.
Os parâmetros assumidos para as simulações numéricas são
os seguintes: q = 2,06×109 K4,  = 5.67×10-8 W/m2 K4, S =
917 W/m2, c = 1000 J/m2Ks,
= 0,75 (brancas),
= 0,25
(pretas),
= 0,5,
= 0,25, L0 = 0,1, w = 0.01 e as
condições iniciais: αb = αw = 0,01 e T = 280 K.
261
A fim de observar a capacidade de reversibilidade do
fenômeno do aquecimento global e o comportamento da
temperatura e das populações de margaridas, são feitas
simulações variando os parâmetros de carga da
luminosidade e dos gases estufa (G) e os resultados são
apresentados nas Figuras 1-9 (sendo o painel esquerdo –
evolução das populações e painel direito – evolução da
temperatura). Na Figura 1,
é constante e o gás cresce
linearmente fazendo com que a temperatura permaneça
estabilizada por um tempo e aumente quando o gás atinge
um determinado valor. Na Figura 2, a estabilização do gás,
partir de um determinado valor, faz com que a temperatura e
as populações também permaneçam estabilizadas.
Fig. 4. 0,75
Fig. 5. 0,75
Fig. 1.
Fig. 2.
e 0,0 ≤ G ≤ 0,8
≤ 1,0 e 0,0 ≤ G ≤ 0,4 e estabiliza em 0,4
Na Figura 6, o gás inicialmente cresce linearmente por
um determinado tempo, em seguida sofre uma redução e
estabiliza em um determinado valor. A temperatura
permanece estabilizada até um determinado valor do gás
quando então começa aumentar. Enquanto o gás vai
reduzindo a temperatura também vai reduzindo até que o gás
estabiliza. Neste ponto a temperatura voltar a subir em
função do aumento da luminosidade.
e 0,0 ≤ G ≤ 0,4 e estabiliza em 0,4
Na Figura 3, Observa-se que com a luminosidade
constante, devido à redução das emissões dos gases estufa a
temperatura retorna ao patamar anterior e estabiliza, fazendo
com que a dinâmica da temperatura e das populações
acompanhem esse comportamento.
Fig. 3.
≤ 1,0 e 0,0 ≤ G ≤ 0,8
Fig. 6.
e G cresce de 0,0 a 0,8 e decresce a 0,4 e
estabiliza em 0,4
Na Figura 7, o gás cresce linearmente até atingir um
valor máximo e em seguida decresce até 0,0. Neste caso a
temperatura inicialmente permanece estabilizada até um
determinado valor do gás quando então começa aumentar.
Enquanto o gás vai reduzindo a temperatura também vai
reduzindo até que o gás atinja o valor 0,0. Neste momento, a
temperatura e as populações voltam a oscilar até um
determinado valor da luminosidade. A temperatura volta a
subir em função do aumento da luminosidade.
e G cresce de 0,0 a 0,8 e decresce a 0,4 e
estabiliza em 0,4
Nas próximas simulações é considerada a luminosidade
crescente, introduzindo um comportamento oscilatório na
temperatura e nas populações. Na Figura 4, a temperatura
permanece estabilizada por um tempo aumentando a partir
de um determinado valor do gás. Na Figura 5, apesar da
estabilização do gás a temperatura continua aumentando em
função do aumento da luminosidade.
Fig. 7. 0,75
≤ 1,7 e G cresce de 0,0 a 0,8 e decresce a 0,0 e
estabiliza em 0,0
262
Influência dos gases estufa na dinâmica do modelo Daisyworld
Flavio Maggessi Viola, Marcelo Amorim Savi.
3. CONCLUSÕES
Uma análise mais geral do Daisyworld foi realizada
considerando o comportamento da luminosidade solar e dos
gases estufa. Com isso pode-se observar a influência dessas
variáveis na dinâmica do Daisyworld. Em geral, esses gases
tendem a aumentar a temperatura do planeta, acelerando a
morte das populações e diminuindo a capacidade de
regulação global. Outro ponto importante é em relação à
reversibilidade do fenômeno do aquecimento global.
Simulações mostraram que mesmo a partir da redução e
estabilização das emissões de gases de efeito estufa, a
temperatura voltou a aumentar o seu valor, em função do
aumento da luminosidade embora o gás tenha permanecido
estabilizado em valores constantes.
AGRADECIMENTOS
Os autores gostariam de agradecer o suporte do Conselho
Nacional de Pesquisa (CNPq).
[10]DOI G.J. Ackland, M.A. Clark & T.M. Lenton,
“Catastrophic desert formation in Daisyworld”, Journal
of Theoretical Biology, Vol.223, pp.39-44, 2003.
[11]DOI B. Adams, J. Carr, T.M. Lenton & A. White,“Onedimensional Daisyworld: Spatial interactions and
pattern formation”, Journal of Theoretical Biology,
Vol.223, pp.505-513, 2003.
[12] A.J. Wood, G.J. Ackland, J.G. Dyke, H.T.P. Williams
& T.M. Lenton, “Daisyworld: A review”, Reviews of
Geophysics, Vol.46, RG1001 23pp, 2008.
[13]DOI R.J. Charlson, J.E. Lovelock, M.O. Andreae S.G.
Warren, “Oceanic phytoplankton, atmospheric sulphur,
cloud albedo and climate”, Nature, Vol.326, pp.655661, 1987.
[14]DOI M. Staley, “Darwinian selection leads to Gaia”, Journal of Theoretical Biology, v.218, pp.35-46, 2002.
[15]DOI Viola, F. M., Paiva, S. L. D; Savi, M. A.,“Analysis
of the global warming dynamics from temperature time
[1]DOI J.E.Lovelock,“Gaia as seen through the atmosphere”,
series”, Ecological Modelling, v.221, n.16, pp.1964in Biomineralization and biological metal accumulation
1978, 2010.
(eds. P. Westbroek and E.E. d Jong), D. Reidei
Publishing Company, pp.15-25. 1983.
[16] Viola, F. M., Savi, M. A., Santos Sobrinho, S., Brasil
REFERÊNCIAS
[2] J.E Lovelock, “Daisy world – a cybernetic proof of the
Gaia hypothesis”, The Co-evolution Quartely, pp.6672, 1983.
[3]DOI J.E.Lovelock,“A numerical model for biodiversity”,
Philosophical Transactions of the Royal Society of
London, Series B – Biological Sciences, Vol.338,
pp.383-391, 1992.
[4] J.E. Lovelock, “The ages of Gaia – A biography of our
living earth”, W.W. Norton, New York, 1988.
[5]DOI A.J. Watson; J.E Lovelock, “Biological homeostasis
of global environment: the parable of Daisyworld”,
Tellus, Vol.35B, pp. 284-289, 1983.
[6] D. Robertson, & J. Robinson, “Darwinian daisyworld”,
Journal of Theoretical Biology, Vol.195, pp.129-134,
1998.
[7]DOI T.M. Lenton; J.E. Lovelock, “Daisyworld is
Darwinian: Constraints on adaptation are important for
planetary self-regulation”, J. theor. Biol. (200), Vol.
206, pp.109-114, 2000.
[8] T. Sugimoto, “Darwinian evolution does not rule out
the Gaia hypothesis”, Journal of Theoretical Biology,
Vol.218, pp.447-455, 2002.
[9]DOI J.E. Cohen & A.D. Rich,“Interspecific competition
affects temperature stability in Daisyworld”, Tellus B,
Vol.52, pp.980-984, 2000.
Junior, A. C. P., “A qualitative description of the global
warming dynamics”. In: COBEM 2009 - 20th
International Congress of Mechanical Engineering,
2009, Gramado – Brazil, 2009.
[17] Viola, F. M., Paiva, S. L. D., Savi, M. A., Lopes, M. T.,
Brasil Junior, A. C. P., “Nonlinear dynamics of the
daisyworld”. In: CONEM 2010 – VI Congresso
Nacional de Engenharia Mecânica, 2010, Campina
Grande – Brasil, 2010.
[18]DOI M.L.Budyko,“The effect of solar radiation variations
on the climate of the Earth”, Tellus, Vol.21, pp.611619, 1969.
[19] G.R. North, R.F. Cahalan & J.A.Jr. Coakley, “Energy
balance climate models”, Reviews Geophys., Vol.19,
pp.91-121, 1981.
[20]DOI M. Lenton, J.E. Lovelock, “Daisyworld revisited:
quantifying biological effects on planetary selfregulation”, Tellus, Vol. 53B, pp.288-305, 2001.
[21] C. Nevison, V Gupta and L Klinger, “Self-sustained
temperature oscillations on Daisyworld”, Tellus, Vol.
51B, pp.806-814, 1999.
[22]DOI J.P. Holman, “Transferência de Calor”, Ed. Mc
Graw Hill, 1983.