Controlo do volume celular

Modelos dos Processos Fisiológicos no Homem
Maio 2005
Controlo do volume
celular
[email protected] Armanda Santos
Inês Aleixo
Joana Góis
Rosemeyre Cordeiro
Sumário
Modelo simples do controlo do volume celular:
- Pressão osmótica e trabalho da concentração
- Modelo simples do controlo do volume celular
Modelo do controlo do volume celular com parte eléctrica:
- Movimento de iões através da membrana
- A interacção dos efeitos eléctricos e osmóticos
- As equações de Hodgkin-Huxley para o potencial
de acção do nervo
Introdução
Membrana biológica são constituída por: bicamada fosfolipídica
Fosfolípidos: moléculas
anfipáticas
‘cabeças’
hidrofílicas
(solúveis
em água)
‘caudas’ hidrofóbicas
Membranas celulares:
-Delimitam o meio interior do meio exterior;
-Delimitam compartimentos intracelulares;
-Criam uma barreira impermeável a iões (estabelecendo assim
gradientes electroquímicos no interior da célula)
Introdução
• Tipos de transporte através da membrana celular: difusão facilitada,
transporte activo primário e secundário;
Transporte mediado por bombas – BOMBA Na+/K+
Bomba sódiopotássio:
potássio
Fluxo activo (contragradiente):
-Translocação de 3
Na+ e 2 K+ por cada
molécula de ATP
hidrolisada
Hodgkin e Huxley: teoria do volume celular através do estudo de
bombas sódio potássio no axónio gigante de lula
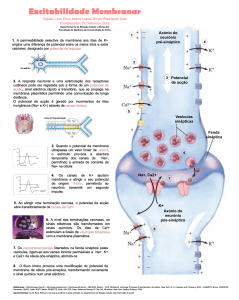
Neurónio-padrão:
padrão
-Corpo celular
-Dendrites
-Axónio
Axónio:
Axónio fibra que se projecta
para fora do corpo celular de
um neurónio e transmite
sinais gerados por esse
neurónio a outros
Potencial de acção
ou impulso nervoso:
Alteração brusca e
intensa do potencial de
membrana (inversão
brusca das cargas
através da membrana
plasmática do
neurónio)
Modelo simples do controlo do Volume
Celular
a)
Fluxo através da membrana:
P1-P2=RQ
Fluxo
Resistência ao
caudal através
da membrana
c)
P1-P2-kTc=RQ
k- cte Boltzman
T- temp. Absoluta da água
P1-P2= kTc
C=n/V1
Assegura o movi/ de água de 2 para 1
Posmótica= P1-P2=kTc= nkT/V1
- Sentido do
fluxo da água
[ ] açúcar
P1-P2-kTc = RQ.
Movimento de água quando se tem
açúcar dos 2 lados da membrana
( P1 − P2 ) − KT (c1 − c 2 ) = RQ
Pressão osmótica relativa determinada
pela diferença [ ] entre as duas soluções
Mistura de
solutos
Solução iónica
Ex: NaCl dissolvido
em água
Posmótica= soma das pressões
osmóticas parciais de cada soluto
independente
Posmótica da solução =
[
]
[ ]
kT Na + + kT Cl −
[ ] concentração individual de cada ião
Modelo simples de controlo do Volume
Celular
Difusão passiva de iões
Bomba de sódio-Potássio
- Responsável por manter o volume
celular
-Processo de difusão activa de iões
Pinterior célula = P exterior
Equações para o fluxo de sódio,potássio e água para o
exterior da célula
[
] [ ]
= α ([K ] − [K ] ) − p
X
Q = − KT ([Na ] + [K ] + − [Na ] − [K ] )
V
f Na = α Na ( Na + i − Na + e ) + p
fK
Concentração do ião no interior e
exterior da célula
+
K
+
i
R( H 2 O )
e
+
Fluxo de iões por unidade de
tempo
Permeabilidades passivas da célula relativamente
aos iões
Supondo que a célula se encontra
num estado de equilíbrio
+
i
+
i
+
e
e
Taxa de movimento de iões pela bomba
Resistência da membrana celular à
passagem da água
Fluxo de iões e água nulo
[Na ] − [Na ]
+
+
i
e
[K ] − [K ]
+
+
i
=−
=+
e
p
α Na
Diferenças de [ ] induzidas
pela bomba
p
αK
[Na ] + [K ] + VX = [Na ] + [K ]
+
+
i
X α K α Na
V=
p α K − α Na
+
i
+
e
e
Caso contrário a água iria Concentração de soluto dentro
e fora da membrana
circ atraves da memb
α K > α Na
=> V>0 => membrana + permeável ao
sódio que o potássio
V inv proporcional a p => p→0,V→∞
É necessário que a bomba mantenha o volume
celular reduzido, caso contrário –> turgescência
da célula e consequente lise celular
V proporcional a X => Com a produção de macromoléculas, a célula cresce e o seu
volume aumenta proporcionalmente
Não ocorre lise celular
Movimento dos iões através da membrana
Estudo do comportamento de um ião genérico A, com vista a aplicação do
resultado num situação de vários iões, os quais atravessam a membrana por
diferentes canais.
W&bateria = W& membrana + W&concentração
Bateria
Condução de
corrente iónica através
da membrana.
g A = 1 / RA
Diferença de voltagem
Condutância da membrana
I A = g A (v − E A )
POTENCIAL DE MEMBRANA
Relação correntevoltagem para um ião A:
AZ +
espécie iónica A
carga positiva
Quando → v = E A , I A = 0
 [ A z + ]2 
KT
EA =
log z + 
zq
 [ A ]1 
Potencial de
equilíbrio
A interacção dos
efeitos eléctricos e
osmóticos
[
0 IK = gK
-
] /[Na ] )) + pq
(v − (kT / q ) log([K ] / [K ] )) − pq
I Na = g Na (v − ( kT / q ) log( Na
+
+
+
e
+
i
+
e
i
[ ] [ ]
−
−
0 I Cl = g Cl (v + ( kT / q ) log( Cl e / Cl i ))
0
Estado de equilíbrio
[
] [ ]
0 = g (v − (kT / q ) log([K ] / [K ] )) − pq
0 = g (v + ( kT / q ) log([Cl ] / [Cl ] ))
5 incógnitas!!
0 = [Na ] + [K ] − [Cl ] − N / V
0 = [Na ] + [K ] + [Cl ] − [Na ] − [K ] − [Cl ]
0 = g Na (v − ( kT / q ) log( Na + e / Na + i )) + pq
+
+
e
K
CONDIÇÃO DE
ELECTRONEUTRALIDADE –
Excesso de carga muito pequeno
comparado com total nº cargas +/-.
i
−
−
e
Cl
+
+
i
+
−
i
+
i
i
i
−
i
+
i
+
e
−
e
e
Solução externa electricamente
neutra:
[Na ] + [K ] = [Cl ]
+
+
e
−
e
e
Para resolver equações anteriores:
[Na ] /[Na ]
+
+
i
e
[K ] /[K ]
+
+
i
= exp( − qv / kT ) exp( − pq 2 / g Na kT )
= exp(−qv / kT ) exp( pq 2 / g K kT )
e
[Cl ] /[Cl ] = exp(qv / kT )
−
−
i
e
βK
β Na
[Na ] = γ
[K ] = γ
+
i
+
i
γ
−1
β Na [Na + ]e
−1
β K [K + ]e
[Cl ] = γ [Cl ]
−
0 = β /( 2γ ) − γ / 2 − b
Equação de
electroneutralidade
−
i
e
Usando a equação do balanço osmótico,
[
] [ ] [ ]
RH 2O Q = −kT ( Na + i + K + i + Cl − i +
Obtém-se:
β <1
β ≥1
V =
b = 1− β
[
x
− Na +
V
] − [K ] − [Cl ] )
+
−
e
e
e
N
[ ]
2 Cl −
e
1− β
Volumes finitos reais
Volume aumenta até ocorrer lise celular
Investigando a dependência de β com p…
Beta tem valor mínimo ao fazer dβ /dp=0
póptimo
Minimiza o volume da célula!!
Funcionamento da célula!!
Volume da célula
depende:
Nº cargas negativas no interior:
Crescimento celular
VOLUME AUMENTA COM
PRODUÇÃO MACROMOLÉCULAS
COM CARGA NEGATIVA
Concentrações iónicas externas:
- Concentração Iões externos inversamente proporcional ao
volume;
Razão [Na+]o/[K+]o
- se diminui, origina aumento
volume celular, devido ao
aumento de beta;
- se tender para 0, pode ocorrer
lise celular;
A Teoria de Hodgkin-Huxley
Canal de Potássio:
- 4 portas idênticas com funcionamento independente
- probabilidade de abertura/encerramento dependentes de voltagem
dn
= α n (v)(1 − n) − β n (v) n
dt
DINÂMICA DE n(t)
Constante de proporcionalidade
gk = gk n4
Probabilidade do canal estar aberto
Condutância de potássio
Canal de Sódio:
- 4 portas não idênticas, mas com funcionamento independente;
Portas m e Portas h
-Probabilidade de abertura /encerramento
função da voltagem v
Difere qualitativamente, com o aumento de v:
- portas m abrem
- portas h fecham
Constante de proporcionalidade
g Na = g Na m 3 h
Condutância do sódio
Probabilidade do canal estar aberto
Equações matemáticas:
m& = α m (v)(1 − m) − β m (v)m
h& = α h (v)(1 − h) − β h (v)h
n& = α n (v)(1 − m) − β n (v)n
Seja: m(t) a fracção de abertura das portas m
h(t) a fracção de abertura das portas h
n(t) a fracção de abertura das portas n
α m (v) α h (v)
α n (v)
Constantes de abertura das
portas m, h e n
β m (v)
β h (v)
β n (v)
Constantes de encerramento
das portas m, h e n
Simulink
Equações
implementadas:
m& = −[α m (v) + β m (v)]m + α m (v)
h& = −[α (v) + β (v )]h + α (v )
h
h
h
n& = −[α n (v ) + β n (v )]n + α n (v )
Simulink – Gráficos / Conclusões
H Gráficos dos fluxos iónicos das portas
m, h e n, respectivamente;
H A porta m abre, facilitando o fluxo
iónico;
HA porta h mantém-se sempre fechada,
impedindo qualquer transporte de iões;
H A porta n tem uma resposta mais
lenta, mas permite também a passagem
iónica;
H A condutância de potássio/sódio
aumenta até estabilizar num nível
elevado, que se mantém ao longo do
tempo.
E viva a lula gigante! ☺
The end..