7º ano - Educação Adventista

ESCOLA ADVENTISTA SANTA EFIGÊNIA
EDUCAÇÃO INFANTIL E ENSINO FUNDAMENTAL
Rua Prof Guilherme Butler, 792 - Barreirinha - CEP 82.700-000 - Curitiba/PR
Fone: (41) 3053-8636 - e-mail: [email protected] – site: www.ease.org.br
LISTA DE EXERCÍCIOS PARA PROVA FINAL/2015
Disciplina: Matemática
Prof.: Márcia Carvalho Vieira
Turmas: 7º ano 1 e 2
1.
Tomando como referência os conceitos de múltiplos e divisores, julgue os itens abaixo
com (V) verdadeiro ou (F) Falso.
(
) – Podemos afirmar que o 1 é sempre divisor de todo número enquanto que o 0 é sempre
múltiplo de qualquer natural;
(
) – Os divisores do número 50 são: {1, 2, 5, 10, 25};
(
) – O número 30 é múltiplo de 2 e 3 somente;
( ) – Podemos afirmar que os números que são divisíveis por 9 são todos aqueles, cuja soma dos
valores absolutos dos algarismos são também divisíveis por 3;
(
) – Os números que são divisíveis por 6, são todos que são divisíveis por 2 e 3, porém, não
necessariamente precisam ser divididos pelo dois ao mesmo tempo;
2.
Determine aquilo que se pede nos itens abaixo:
a)
Múltiplos
de
12
=
{____________________________________________________________}
b)
Múltiplos
de
20
=
{____________________________________________________________}
c)
Divisores
de
60
=
{____________________________________________________________}
d)
Divisores
de
32
=
{____________________________________________________________}
3.
Usando seus conhecimentos sobre sequências numéricas, escreva os 4 próximos
elementos de cada sequência e escreva com suas palavras como cada uma delas tem se
formado.
a)
1, 3, 7, 15, 31, 63, ...
b)
2, 6, 18, 54, ...
c)
1, 2, 6, 24, ...
d)
3, 6, 9, 12, ...
4.
Analise o número abaixo e responda o que se pede, sempre justificando sua resposta:
23 283 834 001
a)
Este número é divisível por 2?
b) Este número é divisível por 3?
c)
Este número é divisível por 8?
d) Este número é divisível por 9?
5.
De acordo com o procedimento descrito, responda os itens abaixo.
a)
Escreva com suas palavras o que está acontecendo com o fractal acima.
b)
Qual a sequencia numérica que determina a quantidade de triângulos pretos?
c)
Qual a sequencia numérica que determina a quantidade de triângulos brancos?
6.
Alberto e Carlos, são administradores da empresa, CINECOM, e precisam
constantemente fazer viagens para atualizar contratos com duas filiais. Carlos precisa
viajar a cada duas semana, e o Alberto precisa viajar a cara 3 semanas. Sobre esta situação
responda o que se prede.
a)
Qual a sequência que determina as semanas de viajem do Carlos?
b)
Qual a sequência que determina as semanas de viajem do Alberto?
c)
Qual será a semana que eles viajarão juntos pela segunda vez?
7.
Dentro do conceito de números primos, determine quais dos números abaixo não pode
ser considerado como número primo, sempre justificando sua resposta.
a)
29
b) 221
c) 65
d) 31
8.
Responda os itens abaixo, justificando suas respostas.
a)
2 é divisor de 275?
b)
5 é divisor de 28?
c)
6 é divisor de 150?
d)
10 é divisor de 116?
9. Calcule as expressões:
a) (-15+4)+[-18+(-3-7+5)]
b) –1 + [1 + (1 – 1) –11
c) –1 +(-2+5)+[-4+(-6+5-8)]
10 - Qual é a diferença?
a) (+3) - (-3)
b) (-9) - (-3)
c) (-7) - (+5)
d) (-5) - (+5)
e) (-2) – (+4)
f) (-12) – (-1)
g) (-1) – (-5)
h) (-3) – (+8)
11. Em relação ao nível do mar, a altitude de um avião é +2500 metros e a de um
submarino é -400 metros. Qual é a diferença entre as altitudes do avião e do submarino?
12. Um avião partiu de um aeroporto situado 600 metros acima do nível do mar, com tempo
bom e temperatura de 28 'C. Ao atingir a altitude máxima, de 3300 metros acima do nível do
mar, o piloto avisou que a temperatura externa era de -40 °C. Da decolagem até o momento
em que foi atingida a altitude máxima, calcule quanto variou:
a) a altitude do avião;
b) a temperatura externa.
13. Indique + se o resultado for positivo e - se for negativo:
+(+3) +(-3) -(+3) -(-3)
14) Agora, elimine os parênteses e calcule:
a) (+1) + (+3) – (+8)
15) Usando seus conhecimentos sobre operações com frações, resolva os itens abaixo:
a)
1
17
+ 3
3
b)
( .
c)
(4 −
+
22
8
+2
2
18 16
2 4
)+( . )
5 4
3 2
11
10
33
)÷(2
2
−
15
)
2
16) Resolva a expressão fracionária abaixo:
𝟐 𝟔
𝟏 𝟗
𝟔 𝟏𝟎
( ÷ )+( ÷ )+( ÷ )
𝟑 𝟐
𝟐 𝟑
𝟐 𝟔
17) Analise as sentenças abaixo e resolva o que se pede:
a)
Uma pessoa deve caminhar 100 metros e já andou 65 metros. Que fração do total do percurso
ainda falta?
b)
Escreva uma fração equivalente a um meio cujo denominador seja dez.
c)
Escreva uma fração equivalente a cinco sétimos cujo numerador seja quinze.
18) Justifique os itens abaixo com verdadeiro ou falso, usando como referência, os
conceitos de números inteiros.
(
) – Dados dois números negativos, o maior deles é o que está mais longe da origem;
(
) – Dados um número positivo e outro negativo, o maior deles é o positivo;
(
) – O número oposto de um número dado é a distância deste á origem;
(
) – O número modular de um número dado é a distância deste á origem;
19) Calcule o valor das expressões numéricas abaixo:
𝑎) − [−6 + (5 − 11 + 6)] + [−9 + (+3 + 1 − 2)]
𝑏) {[(+2 − 6) − (−8 + 2)] + [(+1 − 3) − (+1 + 5)]} − (−20)
𝑐) 13 − {2 − [−5 + 4 + (+7 − 2) − (+7 + 3 − 22) + 6] − 10} + 11
20) Calcule o valor das parcelas desconhecidas abaixo:
21) Resolva as expressões abaixo, usando o jogo de sinais.
𝑎) (+10) + (−17) =
_______________________________________________________________
𝑏) (+2) − (−20) =
________________________________________________________________
𝑐) − (−1) − (+9) =
______________________________________________________________
22) Complete a pirâmide abaixo, sempre somando os números da base, para encontrar os
números da base superior.
23) Num jogo, cada jogador sorteou 5 fichas indicadas abaixo.

Pedro = + 2 - 5 + 3 - 1 + 5

André = - 3 - 4 + 6 + 1 - 1

Carlos = + 3 - 3 - 5 + 6 - 1

Mário = + 2 + 2 + 2 - 4 - 3
24) Assinale a alternativa correta:
a) Pedro totalizou - 4 pontos.
b) Carlos terminou sem nenhuma pontuação.
c) André terminou o jogo com 1 ponto.
d) Mário terminou o jogo com 1 ponto.
25) Em cada uma das situações abaixo, DETERMINE o número desejado.
a) O elevador de um edifício saiu do 9º andar e desceu 12 andares indo parar num dos subsolos.
Que andar é esse? _________
b) Luísa tem 88 reais e deve 100 reais a uma amiga. Como está a “situação econômica” de Luísa?
_________
c) Se a temperatura em Paris é de 5 graus acima de zero e em Moscou é de 8 graus abaixo de
zero. O que deve acontecer com a temperatura em Paris para que seja igual à de Moscou?
________________
26) Em cada uma das expressões abaixo, resolva – as usando as regras de sinais.
a)
1 – {–2 + [–1 + 10 – (3 + 14 – 11)]}
b)
21 – [–17 + (19 – 4) + 12]
27) Calcule o valor das potências abaixo:
a)
(−𝟐)𝟔
b)(+𝟕)𝟑
e)
( )
−𝟒 𝟐
𝟔
f)(−𝟗)𝟐
c) (−𝟏)𝟏𝟎𝟎
d) (+𝟐𝟑𝟏)𝟎
28) Resolva as expressões abaixo, usando seus conhecimentos sobre operações com
números inteiros:
a)
(− 10 + 15 – 1) − [7 + (− 4 + 2) − 3]
(−1)2 − (−1)243 + (−1)7 − (−1)100 +(−1)1 − (−1)0
29) Calcule os valores das raízes quadradas abaixo:
a)
b) −√+9
√−9
c) √−144
e) √−100
30) O valor da expressão numérica [
a)
-1
b) -2
(−𝟏𝟎)+𝟓−(−𝟒) 𝟑
] é:
√𝟗+(−𝟐)
c) +1
d) +2
31) Calcule o valor das seguintes expressões:
a)
16 – {- 4 + [1 + (+ 8 – 1) – 10] + 14 – 2}
b)
– 20 – {- 3 – [- 9 + (- 16 + 1 – 22) + 5]}
d) √+169
32) Resolva as equações abaixo:
a) 3x - 5 = 13
b) 2x + 5 = 5x – 1
c) 3x + 5 = 2
d) 6x + 5 = 5x +
2
33) Usando seus conhecimentos em relação a resolução de equações, simplifique-as e
encontre a solução de cada uma delas.
a)
2.(x + 1) - 3.(2x - 5) = 3.(2x - 1)
b)
5.(1 - x) + 1 = 2x - 3.(x + 2)
c)
2.(3x - 4) - 3.(5 + 2x) = 12
34) Resolva as equações do 1º Grau:
a.
x7 9x

6
3
2
b.
x2 x2
3


3
4
2
c.
x 1 1
 
3 2 4
35) Em uma aula, de Matemática, o Professor apresenta para a turma, a equação
x 3 x
x 8 3

2
 , e solicita que eles respondam. Passado um determinado tempo, o
6
2
3
4
Ângelo, apresenta a equação resolvida e diz que sua solução é
𝟏
𝟒
. Pergunta-se:
d.
O Ângelo estava correto em sua afirmação?
e.
Justifique sua afirmação com a apresentação da solução e dos cálculos.
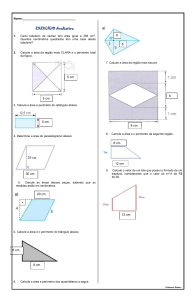
36) Calcule o Perímetro e a área das figuras abaixo apresentadas:
Retângulo = Perímetro: _______________________
Área:
_____________________________
Triângulo = Perímetro: _______________________
Área:
_____________________________
Paralelogramo = Perímetro: ___________________
Área:
_____________________________
Trapézio = Perímetro: _______________________
Área:
_____________________________
37) Resolva os pequenos problemas abaixo, usando noção de área e perímetro de formas
geométricas planas:
a)
Sabendo que um circuito de Fórmula 1 tem o formato de um retângulo de dimensões 2 km e
5 km, calcule a distância percorrida por um piloto que fez 25 voltas nesse circuito?
_________________________________________
b)
Quantos metros de arame serão necessários para cercar uma área retangular de dimensões
4 m e 7 m, sabendo que o proprietário irá fazer uma cerca com 4 fios de arame?
_________________________________________
38) O pátio de uma escola tem a forma retangular e suas dimensões são 45m e 30m. Nesse
pátio foi construída uma quadra de basquete. Sabendo-se que as medidas oficiais de uma
quadra de basquete são 25m por 15, qual a área livre que restou desse pátio? Qual o
perímetro do pátio e da quadra de basquete?
Área Livre do Pátio: _______________________________________
Perímetro do Pátio: _______________________________________
Perímetro da quadra de basquete: _______________________________________
39) Uma parede tem 15m de comprimento por 2,75m de altura. Com uma lata de tinta é
possível pintar 12 m2 de parede.
a)
Quantas latas de tinta serão necessárias para pintar essa parede? _________________
b)
Qual o perímetro da parede? _________________
40) Um campo de futebol tem 105m de comprimento e 70m de largura. Para gramar esse
campo foram compradas placas de grama. Cada placa pode cobrir uma área de 3,5m2.
a)
Quantas placas de grama foram compradas para gramar o campo todo? _________________
b)
Qual o perímetro deste campo de futebol? _________________