E03 - CAMPO ELÉTRICO E MAPEAMENTO DE

E03 - CAMPO ELÉTRICO E MAPEAMENTO DE EQUIPOTENCIAIS
1- OBJETIVOS
 Traçar as equipotenciais de um campo elétrico, em uma cuba eletrolítica.
 Determinar o campo elétrico, em módulo, direção e sentido, devido a algumas distribuições
de cargas elétricas.
 Analisar o potencial e campo no interior de um anel metálico, isolado.
2- MATERIAIS UTILIZADOS
Gerador de
tensão
Pontas de
prova
Multímetro
digital
Papel
milimetrado
Cuba de
vidro
Fios e
conectores
Placas
metálicas
Anel e
pontas
metálicas
Água de
torneira
Figura 1: Materiais necessários para a realização desta experiência.
3- POTENCIAL E CAMPO ELETROSTÁTICO
Uma propriedade do campo eletrostático é ser um campo conservativo (seu rotacional é
nulo). A força elétrica ( ⃗ ) é simplesmente o campo ( ⃗⃗ ) multiplicado por uma constante (a carga de
prova -
) e também é conservativa. É conhecido da mecânica que as forças conservativas são
muito mais simples de se analisar, porque o trabalho ( ) que elas realizam depende apenas dos
pontos inicial e final (
), e não da trajetória. Isso permite definir uma função escalar, chamada
energia potencial ( ), de tal forma que, se apenas a força conservativa atuar, a soma da energia
cinética com a energia potencial permanece constante (essa constante é denominada energia total).
∫ ⃗
∫ ⃗⃗
⃗
⃗
Da mesma forma que a força é proporcional à carga elétrica, a energia potencial também é.
Podemos então definir (
) a energia potencial por unidade de carga, que é chamado de potencial
elétrico:
⁄
∫ ⃗⃗
⃗
A equação
dá o potencial se o campo for conhecido. No entanto, é mais fácil medir o
potencial, porque esse é uma função escalar, enquanto o campo é vetorial; ou seja, para determinar
o potencial, precisamos apenas de um número, enquanto que para determinar o campo precisamos
saber a intensidade, a direção e o sentido. Para calcular o campo supondo conhecido o potencial,
precisamos da relação inversa da equação , que é:
⃗⃗
Uma superfície equipotencial é aquela sobre a qual o potencial é constante. Logo, a
diferença de potencial entre dois pontos quaisquer da superfície é nula. Portanto, sobre uma
equipotencial temos da equação :
∫ ⃗⃗
Uma condição que satisfaz a equação
deslocamento
⃗
é que o campo elétrico seja perpendicular a um
⃗ sobre uma equipotencial. Definindo,
⃗
̂ onde ̂ é um vetor unitário, temos
para o campo elétrico médio entre duas equipotenciais:
⃗⃗
⁄
̂
4- MEDIDAS DE POTENCIAS E CAMPOS ELÉTRICOS
As medidas de potenciais e campos eletrostáticos são experimentos difíceis de serem
realizados em laboratório convencionais de ensino. Isto ocorre porque o meio no qual o campo é
gerado é altamente isolante, e a resistência equivalente entre dois pontos é grande, comparável ou
até maior do que a resistência interna dos voltímetros comerciais, de modo que a leitura seria
totalmente errônea. Tais medidas exigiriam instrumentos de altíssima resistência interna, como
voltímetros eletrostáticos ou eletrômetros e condições ambientais especiais, tais como baixo teor de
umidade, atmosfera inerte ou alto vácuo.
Contudo, podemos contornar esta situação fazendo o mapeamento em um meio com baixa
resistividade como, por exemplo, água de torneira ou uma solução aquosa de CuSO4. Este eletrólito
possui cargas que podem se deslocar quando sujeitas à ação de um campo elétrico, que surge
quando conectamos uma fonte de tensão a eletrodos metálicos mergulhados no eletrólito. A
distribuição de cargas nas superfícies dos eletrodos dá origem a um campo eletrostático no meio
eletrolítico. Dessa forma, o potencial V(P) nos diferentes pontos do eletrólito pode ser mapeado e
possibilita o estudo do campo eletrostático bidimensional correspondente. Esse método é muito
usado na prática para determinar as figuras de potencial de objetos de diferentes formatos, e pode
inclusive ser usado para estudar um campo elétrico tridimensional, mergulhando o objeto
totalmente no meio eletrolítico.
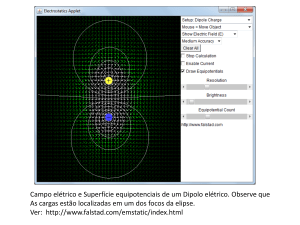
Para ilustrar o método de mapeamento, a Figura 2 ilustra as linhas de campo e as superfícies
equipotenciais de dois eletrodos simulando cargas pontuais, opostas e de mesmo módulo (dipolo
elétrico). Uma bateria cria a diferença de potencial entre os eletrodos e faz com que um fique com
carga positiva e o outro fique com carga negativa.
As linhas equipotenciais podem ser traçadas ligando um conjunto de pontos que possuem o
mesmo valor de potencial, os quais podem ser determinados utilizando um voltímetro convencional.
Uma vez traçado um conjunto de linhas equipotenciais, as linhas de campo podem ser encontradas
trançando-se linhas perpendiculares às mesmas.
O valor do campo elétrico em cada ponto pode ser encontrado de forma aproximada
utilizando a equação 5.
Figura 2: Padrão do campo elétrico gerado por duas cargas de sinais opostos e mesmo módulo
(dipolo elétrico).
5- PROCEDIMENTOS EXPERIMENTAIS
5.1 - MEDIDA DO POTENCIAL ENTRE CARGAS PONTUAIS UTILIZANDO UMA
CUBA
A Figura 3 apresenta um diagrama esquemático da montagem experimental a ser utilizada
para a determinação das linhas equipotenciais e o campo elétrico nos pontos determinados por (A),
(B) e (C).
Figura 3: Diagrama esquemático da montagem experimental com eletrodos em forma de pontos.
01 - Monte o experimento conforme mostrado na Figura 3. Coloque água na cuba, de modo que as
pontas metálicas fiquem ligeiramente mergulhadas (aproximadamente 1 cm de altura). Ajuste a
tensão da fonte para o valor máximo.
02 - Com a ponta de prova
do voltímetro (na vertical) na função (DC), determine pelo menos 3
linhas equipotenciais com pelo menos 07 pontos de mesmo potencial em cada uma, anotando as
coordenadas em uma Tabela. Faça um gráfico destas linhas equipotencial unindo os pontos
experimentais obtidos para cada linha conforme esquematizado na Figura 2.
03 - Faça um gráfico contendo às três as linhas equipotenciais obtidas.
04 - Com as duas pontas de prova, espaçadas de um centímetro, faça uma varredura de 360 sobre
cada circunferência, em torno dos pontos (A), (B) e (C) e determine (Vmax). Para esta situação
registre a posição das pontas de prova. Isto lhe permitirá traçar, depois, a direção do campo e
também determinar, aproximadamente, o seu valor, em torno dos pontos considerados.
05 - Substitua as pontas metálicas pelas placas metálicas conforme mostra a Figura 4. Obtenha as
equipotenciais do campo elétrico. Meça a distância entre as placas e anote.
Figura 4: Diagrama esquemático da montagem experimental com eletrodos em forma de placas.
06 – Faça um gráfico contendo às três as linhas equipotenciais obtidas.
07 – Repita o procedimento do item
em torno dos pontos A B e C.
Figura 5: Diagrama esquemático da montagem experimental com eletrodos em forma de placas e
anel no interior.
08 - Obtenha uma nova configuração introduzindo entre as placas, um anel metálico no centro da
superfície, exatamente no ponto intermediário entre as duas placas, conforme Figura 5, e obtenha
três curvas equipotenciasis conforme feita nos itens 5 e 6.
09 - Determine o potencial elétrico em 05 pontos no interior do anel.
6- QUESTÕES A SEREM ANALISADAS
01 - As linhas equipotenciais obtidas possuem a configuração esperada, em cada caso? Trace
também algumas linhas de força para cada configuração de campo.
02 - Trace o vetor campo elétrico ⃗⃗ em cada ponto considerado (A, B e C), nas configurações
obtidas para as cofigurações x e y. Discuta seus resultados.
03 - Determine também o móodulo do campo elétrico, em torno destes pontos.
04 - Qual o módulo, direção e sentido do campo elétrico entre as placas, referente ao item 05?
(placas paralelas).
05 - O que você verificou sobre o potencial, no interior do anel? O que você conclui sobre o campo
elétrico? Justifique.
06 - Explique o que acontece na superfície do anel, quando este é introduzido entre as placas.
REFERÊNCIAS BIBLIOGRÁFICAS:
1. Albert Malvino e David J. Bates. Eletrônica Volume 1, 7a Edição. McGraw-Hill Interamericana
do Brasil Ltda, São Paulo, SP, 2008.
2. H. Moysés Nussenzveig, Curso de Física Básica 3 - Eletromagnetismo. 1a edição, Editora Edgard
Blucher, São Paulo, SP, 1997.
3. Antonio M. V. Cipelli e Waldir J. Sandrini. Teoria e Desenvolvimento de Projetos de Circuitos
Eletrônicos, 6ª Edição, Editora Érica, São Paulo, SP, 1982.