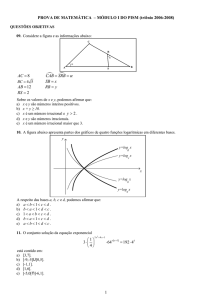
(UFBA – 1996)
05. Considerando-se as funções
01. Considerando-se os conjuntos:
(01) Todos os zeros de g(x) estão contidos no domínio de
h(x) = log(x2 – 4).
(02) A sentença que define (fog)(x) é x2 – 5x + 2.
(04) g(x) é crescente, x [3, + [.
(08) O gráfico de f(x) intercepta os eixos coordenados no
ponto (0, 0).
(16) (gof)(x) é uma função bijetora em R.
(32) Os gráficos de f(x) e g(x) se interceptam nos pontos
(0, -4) e (1, 2).
(64) O conjunto imagem da função h(x) = 2f(x) é R+.
é verdade que:
(01) A B = A
(02) A C = {2, 3}
(04) A – B = {0, 1, 3}
(08) A C = R
(16) (B C) A
C
A
Z
Z
*
06.
A=
02. A respeito dos números reais, é verdade que:
(01) A fração geratriz de 0,39191... é
(08) At =
, pode-se afirmar:
(01) m2 = n . p
(02) m + n = p
(04) Se x
1 e x -1, então
07. Sendo
n.m
= x.
p
(08) Se m . p = 0, então x = 2.
(16) Se x =
1
1
, então o valor numérico de m . n é
.
2
8
(32) O grau da expressão m . n . p é um número inteiro,
pertencente ao intervalo [0, 7].
7x
é R.
x2
(04)f(x) =
é uma função inversa de g(x) =
(08) Sendo f(x) = 2x + 4, então f(x) > 0, x > 0.
(16) Sendo f(x) = 4x2 – 7x, então f(-1) = 11.
m, p
56 e
C m , p 28, pode-se afirmar:
(01) Pm = 61
(02) Am + 2, p + 1 = 27
(04) Cm, p + 1 = 56
(08) Cm, 0 + Cm, 1 + Cm, 2 + ... + Cm, m – 1 + Cm, m = 256
(16) Pp + 1 = 6
(32) Pp . Am + 1, p + 1 = 2! . 9!
(01) h . d . D = 60 cm3.
(02) O volume de P é V = 16 cm3.
(02) f(x) = 3x2 + 4x é uma função par.
3x 2
2x
A
08. Em um paralelepípedo retângulo P, a altura h, a diagonal
da base d e a diagonal D são, nessa ordem, os termos
consecutivos de uma progressão aritmética de razão r = 1.
Sendo a base do paralelepípedo P um quadrado, pode-se
afirmar:
04. Sobre as funções reais, é verdade que:
(01) O domínio de f(x) =
8 4
6 b
1 2
3 4
6 2
(16) Bt =
8 4
1
(32) det B-1 =
40
(16) Se x2 + 81 = 0, então x = -9 ou x = 9.
03. Sendo
B=
(01) a . b = 8
(02) detA + detB = 50.
(04) A matriz A . B é inversível.
x 1 8 , então x = -7 ou x = 9.
m x 1
2
n x x
p x2 1
a 2
3 1
Se as matrizes A e B, dadas acima, são tais que 2A – B = 0,
pode-se afirmar:
194
.
495
(02) Se x = 1, então (x – 1)(x – 4)(x + 5) = 0.
(04) Se x + y = 10 e x – y = 2, então x = 8 e y = 2.
(08) Se
é
verdade:
A = {X N; X < 4}
B = {X Z; 2X + 3 = 7}
C = {X R; X2 + 5X + 6 = 0}
(32)
f ( x) x 4
2
g ( x) x 5 x 6
2
.
2x 3
(04) A área total de P é 4(4 + 3 2 ) cm2.
(08) A área do círculo inscrito na base de P é S = 2 cm2.
(16) O perímetro do triângulo cujos lados coincidem com h, d,
D é p = 12 cm.
09. Uma pessoa retira R$ 70,00 de um banco, recebendo 10
notas, algumas de R$ 10,00 e outras de R$ 5,00. Calcule
quantas notas de R$ 5,00 a pessoa recebeu.
10. O triângulo ABC está inscrito num círculo de área igual a
16 cm2, sendo  = 30º, AB = 8 cm e AC . BC = x cm 2.
Determine o valor de x
3.
(01) O produto das raízes da equação (x2 – 6x + 8)(x + 3) = 0 é
– 24.
(02) A solução da inequação x2 – 3x + 2 > 0 é o conjunto
(- , 1] [2, + ).
MATEMÁTICA – UFBA – 1996
QUESTÕES
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
01 + 04 + 16
01 + 02 + 08
04 + 32
04 + 08 + 16
02 + 04 + 64
01 + 02 + 04 + 32
04 + 08 + 16
01 + 08 + 16
-------------------------------------------------
03. Sobre as equações e inequações, é verdade que:
GABARITO
21
11
36
28
70
39
28
25
06
48
x
(04) A equação
(08) Se
x2
= - x não tem solução.
< 1, então x
]-3, -1].
(16) Se 2x – y = 4 e 2x + y = 16, então x2 + y2 = 10.
(32) Se log 1 (x + 1) < 1, então -1 < x <
3
2
.
3
04. Sobre as funções reais, é verdade que:
(UFBA – 1997)
01. Numa escola, 45% dos estudantes são crianças, 35% são
adolescentes, e os 600 alunos restantes são adultos. Nessas
condições, pode-se afirmar:
(01) A escola possui um total de 3000 alunos.
(02) O número de adolescentes é de 1250.
(04) 270 crianças, menores de 5 anos, correspondem a 25%
do total de crianças.
(08) O percentual do número de adolescentes, em relação ao
número de adultos é de 175%.
(16) 420 adolescentes estudam à tarde e correspondem a 2/5
do total de adolescentes.
(01) A função f(x) = 1 – x é decrescente.
(02) A função f(x) = x2 – x + 1 tem valor máximo em x = 1/2.
(04) Se f(x – 1) = x + 1, então f(3) = 5.
(08) Se f(x) = x2 – 1 e g(x) = x2, então gof(x) = x4 - 1.
(16) Se f é a função inversa de g, então f(g(x)) = x.
(32) Se f: R R é uma função crescente, então f(3) > f(4).
(64) Se f é uma função ímpar e f(1) = 2, então f(-1) = -2.
05. Sobre exponenciais e logaritmos, é verdade que:
02. Considerando-se as taxas de natalidade e mortalidade, a
população da cidade A apresenta crescimento de 3% ao ano,
e a população B aumenta, a cada ano, 2000 habitantes em
relação ao ano anterior. Se, em 1970, a população da cidade
A era de 200000 habitantes e a população da cidade B era de
220000 habitantes, pode-se afirmar:
(01) Em 1972, a população de A era maior que a população
de B.
(02) Em 1980, a população de A cresceu aproximadamente
6 x 103 x (1,03)9 habitantes.
(04) Em 1980, a população de A era de aproximadamente
2 x 10 5
0,03
[1 – (0,03)11] habitantes.
(08) Em 1990, a população de B era de 2,6 x 105 habitantes.
(16) O gráfico abaixo representa a variação da população de
B em relação ao tempo t, a partir de 1970.
(01) log 0,1 + log
2
4 = 0.
(02) O domínio da função f(x) = log (1-x) é o conjunto
ab 2
c
(04) log
= log a + 2log b – log c,
a, b, c
R* .
R* .
(08) f(x) = (m – 1)x é uma função exponencial crescente, para
m > 2.
(16) O gráfico da função f(x) = log2(x + 2) intercepta o eixo OY
no ponto (0, 1).
(32) O gráfico abaixo representa a função y = 1 +
2x
06. Sendo P(x) (m – 1)x3 + x2 + x – 1 um polinômio de grau 2 e
Q(x) = kx3 + x2 + 2x + 2 um polinômio que tem -1 como raiz,
pode-se afirmar que:
09. Dispondo-se de abacaxi, acerola, goiaba, laranja, maçã,
mamão e melão, calcule de quantos sabores diferentes podese preparar um suco, usando-se três frutas distintas.
(01) k.m = 1
(02) P(x).Q(x) é um polinômio de grau 6.
(04) P(x) tem duas raízes reais.
(08) xP(x) – Q(x) = 2 + 3x
(16) O quociente da divisão de Q(x) por x + 1 é x2 + 2.
(32) O resto da divisão de Q(x) por P(x) é 3x + 2.
10. Uma estrada eleva-se 0,5 m a cada
graus, o ângulo de inclinação da estrada com a horizontal.
MATEMÁTICA – UFBA – 1997
07. No semicírculo representado abaixo, consideram-se os
triângulos retângulos CMO e MHO, sendo
AM
OC = 3 cm
(02)
CM = 15 cm
(5
= 5 cm e
O
perímetro
do
triângulo
AMC
é
15 / 2
cm2.
PROPOSIÇÕES
CORRETAS
01 + 08 + 16
02 + 08 + 16
01 + 02 + 08 + 16
01 + 04 + 16 + 64
04 + 08 + 16
01 + 04 + 16 + 32
02 + 16 + 32
04 + 08 + 32
-------------------------------------------------
01
02
03
04
05
06
07
08
09
10
igual
a
GABARITO
25
26
27
85
28
53
50
44
35
30
(UFBA – 1998)
6 + 15 )cm.
(08) A área do triângulo MHO é igual a
(16) A área do círculo de centro em O e raio OB é igual a
16 cm2.
2
(32)
QUESTÕES
= 3 cm. Nessas condições, pode-se afirmar:
(01)
(04)
BM
3 / 2 m. Calcule, em
2
AB AC CB
2
01. No conjunto dos números reais, é verdade que:
(01) Se x = 0,5454... e y = 0,4545..., então x + y = 1.
(02) A expressão (m – 3)x3 + (m – n +1)x2 + 4x + 2n é do
1º grau, em x, para m = 3 e n = 4.
(04) Se x {-2, -1, 0, 1}, a expressão (x – 1)(x + 1)(x + 2)x
assume um único valor.
(08)
08. Considerando, no sistema cartesiano XOY, o ponto
P(-1, 1) e as retas r: y = 2x + 2 e s: x + 2y – 3 = 0, é verdade:
1
2
<
4
<
8
3
<
3
5
(16) Se os números 2m + 1, 4 e 2n + 5 são diretamente
proporcionais a 1, 2 e 3, então m + n = 2.
(01) O simétrico de P, em relação ao eixo OY, é o ponto
02. Sobre funções reais, é verdade que:
Q(-1, -1).
(02) P s
(01) O conjunto imagem da relação M = {(x,y)
(04) A distancia de P à origem é de
2 u.c.
(08) As retas r e s são perpendiculares.
(16) A reta que passa por P e é paralela a r tem equação
2x – y + 1 = 0.
(32) A reta r intercepta o eixo OX no ponto (-1, 0).
A x B; y = x/2
+ 1/x}, sendo A = {-2, 1, 3, 4}, é {-1, 1/2, 3/2, 12}.
(02) Sendo f(x) =
x 2x 2
3
, f(9) = -53.
(04) O conjunto imagem da função representada no gráfico
abaixo é [-2, -1] [1, 3].
(08) O sistema
x y z 0
x y 2z 0
tem como única solução
(0, 0, 0).
= 0, então o sistema
ax y 2
2 x by 3
é
(32) Se S1 é o conjunto solução do sistema
x y 3
2 x 3 y 7
e
(16) Se det
a 1
2 b
determinado.
1
(08) O domínio da função f(x) =
x 5x 6
é R – {2, 3}.
2
(16) A função f(x) = x2 – 1, definida de A = {-2, 1, 0, 3} em
B = {-1, 0, 3, 8}, é bijetora.
S2 é o conjunto solução do sistema
S1
S2 = {(2, 1)}.
x y 1
3x 3 y 3
, então
representado
abaixo,
03. Sendo f(x) = (x – 3)(x + 2) uma função real, pode-se
afirmar:
(01) O conjunto imagem da função é ]- , 3].
(02) O gráfico da função intercepta o eixo das abscissas nos
pontos (-2, 0) e (3, 0).
(04) A função é crescente no intervalo [-3, 2].
(08) O gráfico da função tem vértice no ponto (1/2, -25/4).
06.
No
quadrilátero
AB AD AC =
ABCD
3u.c.,
ABˆ C , ACˆ D
e
ABˆ D . Nessas condições, pode-se afirmar:
(16) Para todo x < -2, f(x) > 0.
(32) O eixo de simetria do gráfico da função é x = 3/2.
04. Sobre as funções exponenciais e logarítmicas, é verdade:
(01) Se log 13 = 1,114, então log 1300 = 3,114.
(02) log 6 = log 2 . log3
(04) O domínio da função f(x) = log4(x + 3) é ]-3, + [.
(08) Se 3x + 1 = 9x, então x é um número par.
(16) Se 2x + 4x – 6 = 0 e log28 = y, então x + y = 4.
(01)
180º
(02) O triângulo BCD é acutângulo.
(04) A área do triângulo ABC é igual a 2,25 u.a.
(08) O perímetro do triângulo ACD é igual a 9u.c.
(16) A altura do triângulo ABC, relativa à base
05. Sobre matrizes, determinantes e sistema de equações
lineares, pode-se afirmar:
(01) Se A
1 2
= 2
5
1 x 2
1
4 3x
0
, é igual a
1,5 u.c.
(32) O raio da circunferência circunscrita ao triângulo ABD é
igual a 4
2 u.c.
é matriz simétrica, então
x ] - , 2].
(02) Se B é uma matriz tal que [0 1 0] B = [2 1 0], então a
2ª coluna da transposta de B é
AC
2
1 .
0
(04) Se as ordens das matrizes M, N, P e MN + P são,
respectivamente, 3 x a, 2 x b, c x d e 3 x 3, então
a + b + c + d = 10.
07. No sistema de coordenadas XOY, tem-se uma
circunferência C, de centro no ponto A(1, 1) e tangente à reta
s: 4x + 3y + 3 = 0. Sendo assim, pode-se afirmar:
(01) O raio de C mede 2 u.c.
(02) A equação de C é x2 + y2 = 4.
(04) A área do quadrado inscrito em C tem 12 u.a.
(08) A reta que passa pelo ponto A e é perpendicular à reta s
tem equação 3x – 4y + 1 = 0.
(16) Sendo B(x, 1) ponto da região interior a C, então
-1 < x < 3.
08. Uma rede de lojas comprou uma mercadoria à vista, com
20% de desconto sobre o preço de tabela e teve uma despesa
de R$ 50,00 com transporte e impostos. Na venda dessa
mercadoria, obteve um lucro de 20% sobre o total
desembolsado. Se o preço de venda foi R$ 540,00, então
pode-se afirmar:
(01) O preço de tabela era R$ 500,00.
(02) O preço a vista foi de R$ 400,00.
(04) O lucro obtido foi de R$ 60,00.
(08) O desconto sobre o preço de tabela foi R$ 40,00.
(16) As despesas com transporte e impostos corresponderam
a 12,5% do preço à vista.
09. Durante 15 dias, um automóvel é submetido a testes de
desempenho mecânico. No primeiro dia ele percorreu 40 km;
no segundo, 60 km; no terceiro, 80 km; e assim
sucessivamente, até o último dia, quando percorre x km.
Calcule
x
10
(UFBA – 1999)
01. Uma indústria foi implantada com um ritmo de produção tal
que garantiu um aumento mensal constante ate o 59º mês,
quando afinal a produção se estabilizou. A soma da produção
do 2º mês com a do 4º foi igual a 40 unidades, e a do 3º mês
com a do 6º, igual a 55 unidades. Com base nessas
informações, pode-se afirmar:
(01) A indústria produziu 15 unidades no 1º mês de
funcionamento.
(02) Até o 59º mês, o aumento mensal da produção era de 5
unidades.
(04) Ao fim de 6 meses de atividades, a industria já tinha
produzido um total de 145 unidades.
(08) Aos 24 meses de atividades, a indústria estava
produzindo 125 unidades.
(16) A indústria estabilizou sua produção ao alcançar o marco
de 300 unidades mensais.
.
02. Sobre a função real, de variável real, f(x) =
x2 1
, pode
x3
-se afirmar:
10.
No
cubo
1
AB 3u.c., AI . AE,
3
representado
abaixo,
(01) O domínio da função f é R.
(02) O gráfico da f intercepta o eixo Ox no ponto (-1, 0).
e o volume do tetraedro EFHI é
(04)
igual a x u.v. Calcule x.
2 f ( 2 )
f (1)
=6
(08) Se f(x) = 3, então x
(16) f(x) e g(x) =
x3 x
x 2 3x
{-2, 2, 5}
são funções iguais.
(32) Sendo g(x) = 3x + 1, g(f(x)) =
x g ( x)
.
x3
03. Sobre as funções reais, pode-se afirmar:
(01) f(x) =
MATEMÁTICA – UFBA – 1998
QUESTÕES
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
01 + 02 + 04
02 +16
02 + 08 + 16
01 + 04 + 16
01 + 02 + 32
01 + 04 + 08 + 16
01 + 08 + 16
01 +02 + 16
-------------------------------------------------
GABARITO
07
18
26
21
35
29
25
19
32
03
3x 1
xa
é a função inversa da g(x) =
2x 1
,
x3
se
x = 2.
(02) f(x) =
x
x
pode ser representada graficamente por
(04) Sendo f(x) = 2x2 – 5x + 2, tem-se f(x) > 0, se 1/2 < x < 2.
(08) f(x) = (2m – 1)x é decrescente, se 1/2 < m < 1.
(16) f(x) = log log (3x + 4) está definida, se x > -1.
(32) o valor máximo da f(x) = 6cos(x) + 15 é 21.
04. Sobre os polinômios p(x) = x3 – 5x2 + 6x e
q(x) = -x3 – 4x2 + 5x, é verdade que:
07. Sobre trigonometria, pode-se afirmar:
(01) Se f(x) = cós(x), então f-1(x) = sec(x).
(01) q(x) tem duas raízes reais inversas.
(02) p(x) e q(x) têm uma raiz comum.
(04) p(x) tem duas raízes imaginárias.
(02) As expressões E1 =
(08) p(x) é divisível por x – 2 ou q(x) é divisível por x + 1.
(16) O quociente da divisão de p(x) por x – 3 é x2 – 2x e o
resto é p(2).
(32) O grau do polinômio p(x) + q(x) é igual a 3.
1 tg 4 x
cos 4 x sen 4 x
equivalentes.
(04) A função f(x) = 3sen(2x) é injetora no
3
4 , 4
(08)
O
conjunto
de
todas
a 1
2 b
x
y
X=
com a + b = 4, a.b = 3 e a < b, B = A-1,
(16) Se senx =
2
, é verdade:
1
eC=
(32) Se tgx =
m
2
(01) det A = 1
3 2
(02) B =
1 1
(64) Se cosx =
e0<x<
7
.
5
R; x =
soluções
2
1
2
e
da
+ k ; k
equação
Z}.
3
, então cos arcsen
2
5
=
4
.
5
3 3
Z
,
.
3
3
3
< x < 2 , então o valor numérico
2
cot gx cos sec x
é um número
senx
pertencente ao conjunto R – Q.
(08) Se AX = C, então X =
0
2
, então X = .
0
3
08. Uma indústria de equipamentos elétricos produz 1000
unidades por dia, vendendo cada unidade a R$ 1,20. O lucro
diário da indústria é de R$ 300,00. Nessas condições, pode-se
afirmar:
(16) Se BX =
(32) det (A + 5B)t = 96
06. Se uma das faces de um cubo está inscrita numa
3 2
as
e secx = m, então m
da expressão E =
(04) det A . det B = 1
circunferência de raio r =
3
5
intervalo
3 5
4 , 4 .
e é crescente no intervalo
sen2x cotgx = cosx é S = {x
05. Sendo A =
e E2 = cos4x são
cm2, é verdade:
(01) O volume do cubo é V = 216 cm2
(02) A área total do cubo é S = 144 cm2
(04) A área do círculo inscrito em uma face do cubo é
A = 9 cm2
(01) A receita total da produção diária é de R$ 1200,00.
(02) O lucro diário sobre a receita total de produção diária
equivale a 30%.
(04) Com o pagamento à vista a receita total da produção
sofreu descontos sucessivos de 8% e de 3%, resultando num
desconto total de 10,76%.
(08) Se a margem de lucro diário aumentar em 35%, a
indústria, independentemente de outros fatores, lucrará R$
405,00 por dia.
(16) Se, mantida a mesma capacidade produtiva, a receita
total diária passear para R$ 1248,00, o preço de venda de
cada equipamento terá sofrido um aumento de 4,8%.
(08) O apótema da pirâmide de altura igual à aresta do cubo e
de base igual a uma das faces desse cubo é a = 6
5 cm.
(16) A área lateral do cilindro de base circunscrita a uma face
do cubo e de altura igual a uma aresta desse cubo é
L = 18
2
cm2.
(32) A área do triângulo retângulo em que um cateto é igual à
diagonal de uma das faces do cubo e o outro cateto é igual a
uma aresta desse cubo é s = 18
2
cm2.
09. Uma herança de R$ 525000,00 foi dividida entre duas
famílias, uma com 25 pessoas e a outra com 30 pessoas, de
maneira tal que a quantia recebida por um dos membros da
família menor somada à recebida por um dos membros da
família maior foi igual a R$ 20000,00. Todos os membros de
uma mesma família receberam quantias idênticas. Cada
pessoa da família menor recebeu x mil reais. Calcule x.
10. A, B e C são pontos de interseção da circunferência
x2
02. O número de bactérias de determinada cultura varia de
y2
+
= 4, respectivamente, com o semi-eixo positivo das
abscissas, o semi-eixo positivo das ordenadas e a reta y = x.
Se C pertence ao 3º quadrante e m é a medida, em u.a., da
área do triângulo ABC, calcule m(1 +
2
01
02
03
04
05
06
07
08
09
10
100.2
t
2
, em que o tempo é dado em
horas. Nessas condições, pode-se afirmar:
)-1.
(01) No instante t = 0, o número de bactérias existente na
cultura é igual a 200.
(02) Depois de 8 horas, o número de bactérias existente na
cultura é menor que 7.
(04) Em 4 horas, a quantidade de bactérias na cultura se
MATEMÁTICA – UFBA – 1999
QUESTÕES
acordo com a lei N(t) =
PROPOSIÇÕES
CORRETAS
02 + 08 + 16
02 + 08 + 32
01 + 08 + 16 + 32
02 + 08 + 16
01 + 04 + 08 + 32
01 + 04 + 32
04 + 08 + 16
01 + 04 + 08
-------------------------------------------------
GABARITO
reduz a 1/4 da quantidade inicial.
(08) Na cultura, a quantidade de bactérias se reduz de 2/5 da
26
42
57
26
45
37
28
13
15
02
quantidade inicial no tempo t = 2log2
5
3
(16) Em relação ao tempo, a variação da quantidade de
bactérias é representada pelo gráfico
(UFBA – 2000)
01. Sendo f(x) = x2 + bx + c e g(x) = mx + n funções reais
cujos gráficos estão representados abaixo, pode-se afirmar:
03. Sobre expressões algébricas e polinômios, pode-se
afirmar:
(01) (x + 2)3 = x3 + 8,
(02)
x
R.
x 1
2
x2 1
,
x( x 1) x 2 1 x 3 x
x
R – {-1, 0, 1}.
(04) Se (mx2 – nx + 1)(x – 1) = x3 – 2x2 + 2x – 1, então mn = 1.
(08) O resto da divisão x3 – 2x2 – 6x + 1 por x + 1, então
m = 1/2.
(16) Se 2 é raiz do polinômio P(x) = x3 + 3x2 + 3x + 2, então as
outras raízes são números complexos conjugados.
(01) A imagem de f é [-1/2, +
[.
(02) f (-2) = 15.
(04) A solução da inequação f(x)
3 é [0, 4].
(08) g(4) = -1
(16) A solução da inequação
g ( x) 3
é ]-
,
0]
04.
Dadas
as
matrizes
A
=
[6, + [.
(32) f(g(x)) = x2 - 2x
(64) g-1(x) = x – 3
B =
1 1
0 1
1 0
e C =
1 0 1
1 1 0
det A = 4a, pode-se afirmar:
1
a 1 0
1
a ,
0
0
0 a 1
e sabendo-se que
(01) A soma dos elementos da diagonal principal de A é igual
Nessas condições, é verdade:
a 6.
(02) B + 2Ct = 9B
(01) As coordenadas de Q são (8, 4).
(04) A matriz inversa de CB é
1 2 1
.
3 1 2
(08) As soluções do sistema C
(z, -x, -x), x
x
0
y
z 0
(02) O ponto médio de
OQ
é M = (4, 2).
(04) A reta paralela ao eixo OX que passa por P é x = 3.
são da forma
(08) A reta perpendicular a OP que passa pelo ponto P tem
por equação 3x + 4y – 25 = 0.
(16) A equação da circunferência de centro em M e tangente
ao eixo OY é x2 + y2 – 8x – 4y = -4.
(32) A área do triângulo OPQ é igual a 32 u.a.
R.
x 0
(16) O sistema A y 0
z 0
07. Em uma escola, o 3º ano colegial tem duas turmas: A e B.
A tabela mostra a distribuição por sexo, dos alunos dessas
tem solução única.
turmas.
05. Na figura abaixo, o triângulo retângulo ABC tem maior
ângulo em , área igual a 6 u.a. e é semelhante ao triângulo
de catetos iguais a 6 u.c. e 8 u.c. Nessas condições, pode-se
Turma
Homens
Mulheres
A
B
20
25
35
20
afirmar:
Com base nesses dados, pode-se afirmar:
(01) Escolhendo-se, ao acaso, um aluno do 3º ano, a
probabilidade de ser homem é igual a 0,45.
(02) Escolhendo-se, ao acaso, um aluno do 3º ano B, a
probabilidade de ser mulher é igual a 20%.
(04) Escolhendo-se, ao acaso, simultaneamente, dois alunos,
um de cada turma, a probabilidade de serem os dois do
(01) A altura do triângulo relativa à hipotenusa mede 3 u.c.
(02) A área do círculo circunscrito ao triângulo é igual a
6,25 u.c.
(04) O comprimento da circunferência de centro em B e raio
AB
é 6 u.c.
(08) A área do hexágono regular de lado igual a
18 u.a.
(16) tg + sen(180º -
AB
mede
) = 32/15
06. No triângulo OPQ, representado na figura ao lado,
OP PQ
mesmo sexo é igual a
16
.
33
(08) Escolhendo-se, ao acaso, um aluno do 3º ano, a
probabilidade de ser mulher ou de ser da turma B é igual a
80%.
(16) Reunindo-se as mulheres das turmas e escolhendo-se
uma, ao acaso, a probabilidade de ser da turma A é igual a
35%.
08. Um carro anunciado para venda por R$ 20000, 00 em três
parcelas iguais, também poderá ser negociado nas seguintes
condições:
e PQ é paralela ao eixo OX.
(01) À vista, por R$ 17600,00, se for dado um desconto de
12%.
(02) Em três parcelas iguais, com 16% de desconto por
isenção de ICMS, totalizando R$ 16400,00.
(04) Em quatro parcelas iguais e mensais, com um acréscimo
de R$ 1600,00 no total, o que corresponde a 2% de juros ao
mês.
(08) Em cinco parcelas iguais de R$ 4360,00, havendo um
acréscimo de 11%.
(16) Em oito parcelas iguais e mensais, com juros de 2,2% ao
mês, totalizando R$ 23520,00.
09. Um jogador faz uma série de apostas e, na primeira vez,
perde R$1,00; na segunda, duplica a aposta e perde R$2,00;
ma terceira, duplica a aposta anterior e perde R$4,00; e
assim, sucessivamente, até ter perdido um total de R$255,00.
Calcule quantas vezes o jogador apostou.
10. Uma pessoa possui dez CDs de musica clássica e quer
escolher quatro deles para levar numa viagem. Sendo n o
Com base nessas informações, pode-se concluir:
(01) A pesquisa envolveu 500 pessoas.
(02) 61 pessoas estavam matriculadas apenas em
alongamento.
(04) 259 pessoas estavam matriculadas em alongamento ou
musculação.
(08) 89 pessoas estavam matriculadas em pelo menos duas
atividades indicadas na tabela.
(16) O número de pessoas matriculadas apenas em
hidroginástica corresponde a 28,4% do total de pessoas
envolvidas na pesquisa.
número de maneiras distintas em que a escolha pode ser feita,
calcule
n
.
3
MATEMÁTICA – UFBA – 2000
QUESTÕES
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
02 + 04 + 08 + 16 + 32
02 + 04 + 08
02 + 04 + 16 + 32
04 + 08 + 16
02 + 04 + 16
01 + 02 + 08 + 16
01 + 04 + 08
ANULADA
-------------------------------------------------
GABARITO
62
14
54
28
22
27
13
ANULADA
08
70
02. Um agricultor plantou uma série de mamoeiros, distando 3
m um do outro e formando uma fila, em linha reta, com 72 m
de comprimento. Alinhado com os mamoeiros, havia um
depósito, situado a 20 m de distancia do primeiro. O agricultor,
para fazer a colheita, partiu do depósito e, margeando sempre
os mamoeiros, colheu os frutos do primeiro e levou-os, ao
depósito; em seguida, colheu do segundo, levando-os para o
depósito; e, assim, sucessivamente, até colher e armazenar
os frutos do último mamoeiro. Considere que o agricultor anda
50 metros por minuto, gasta 5 minutos para colher os frutos de
cada mamoeiro, e mais 5 para armazena-lo no depósito.
Nessas condições, pode-se concluir que o agricultor:
(01) plantou 25 pés de mamão.
(02) plantou o 12º mamoeiro a 56 metros do depósito.
(04) quando fez a colheita do 10º mamoeiro, havia passado6
vezes pelo 5º mamoeiro.
(08) ao completar a tarefa de colheita e armazenamento dos
frutos de todos os mamoeiros, tinha andado 2800 metros.
(16) para realizar toda a tarefa de colheita e armazenamento,
gastou 5 horas e 6 minutos.
(UFBA – 2001)
01. Numa academia de ginástica que oferece
de atividades físicas, foi feita uma pesquisa
número de pessoas matriculadas em
hidroginástica e musculação, chegando-se
expresso na tabela a seguir:
Atividade
varias opções
para saber o
alongamento,
ao resultado
Nº de pessoas matriculadas
Alongamento
109
Hidroginástica
203
Musculação
162
Alongamento e hidroginástica
25
Alongamento e musculação
28
Hidroginástica e musculação
41
As três atividades
5
Outras atividades
115
03. Uma micro-empresa fabrica um determinado bem de
consumo e o coloca à venda, no mercado. O custo de
fabricação do produto é composto de uma parcela fixa,
correspondendo a R$ 3,00 por unidade fabricada. A
quantidade vendida depende do preço da unidade e obedece
à lei de uma função afim. Quando o preço da unidade é de R$
6,00, são vendidas, mensalmente, 200 unidades do produto.
Aumentando-se o preço em R$ 2,00 por unidade, passam a
ser vendidas 100 unidades mensais. Com base nessas
informações, pode-se concluir:
(01) A quantidade vendida em relação ao preço unitário é
uma função decrescente.
(02) Se o preço unitário for de R$ 3,00, 250 unidades serão
vendidas.
(04) O custo de fabricação de 1000 unidades do produto é
igual a R$ 3300,00.
(08) A receita máxima pela venda do produto é igual a R$
1250,00.
(16) Sendo L(x) o lucro em função das unidades vendidas,
então L(x) = - 0,02x2 + x – 100.
(32) Quando o preço unitário se situar entre R$ 6,50 e R$
9,00, o lucro será crescente.
04. Com base no gráfico da função f: R R, representada
abaixo, pode-se afirmar:
(01)
(01) A imagem de f é o intervalo ]0, 1].
2
2
PT
mede 3
11
u.c.
(02) A altura do triângulo PTO, em relação ao lado PO, mede
(02) A equação f(x) = 1 tem infinitas soluções.
(04) A equação f(x) =
06. Na circunferência de centro O, representada pela figura
abaixo, o raio mede 4 u.c., a distância de P a A mede 3 u.c. e
a reta PT é tangente à circunferência. Nessas condições, é
correto afirmar:
4 33
u.c.
7
não tem solução.
(08) A função f admite inversa.
(16) O ponto (0, 2) pertence ao gráfico de g(x) = 1 + f(x + 1).
(32) O gráfico da função f ( x ) é
(04)
O
perímetro
do
triângulo
MOT
é
igual
a
4(11 33 )
u.c.
7
(08) A área do triângulo POT mede 2
33 u.a.
(16) A hipotenusa de um triângulo homotético ao triângulo
POT em que a razão de homotetia é igual 3/2 mede 21u.c.
07. De acordo com o Boletim do Serviço de Meteorologia de 07
de Junho de 2000, o quadro abaixo apresenta a temperatura
máxima, em graus Celsius, registrado em Fernando de Noronha
e nas capitais da Região Nordeste do Brasil.
05. Considerando-se as funções f(x) = log3(1 – x2) e
g(x) = 27x – 1, é correto afirmar:
(01) O domínio da função f é
R*
3
3 = - 1 + log 32
(02) f
log( 1 x )
log 3
(08) O conjunto-solução da inequação g(x)
[0, + [.
27 ºC
30 ºC
31 ºC
30 ºC
27 ºC
30 ºC
30 ºC
26 ºC
32 ºC
32 ºC
Com base nessas informações pode-se afirmar:
2
(04) f(x) =
Aracajú
Fernando de Noronha
Fortaleza
João Pessoa
Maceió
Natal
Recife
Salvador
São Luis
Terezina
(01) O gráfico abaixo representa a distribuição de freqüência
das temperaturas.
2 é o intervalo
(16) A função g é crescente em todo o seu domínio.
(32) g-1(x) = log3 (
3
x 1 )
( x 1) 3
27
2
(64) g(f(x)) =
(02) A freqüência relativa da temperatura de 31 ºC é igual a
10%.
(04) Representando-se a freqüência relativa por meio de um
gráfico de setores, a região correspondente à temperatura de
27 ºC tem ângulo de 36º.
(08) A média aritmética das temperaturas indicadas no quadro
corresponde a 29,5 ºC.
(16) A mediana das temperaturas registradas é igual à
temperatura modal.
(32) A amplitude das temperaturas é de 32 ºC.
08. Uma pessoa tomou um empréstimo de R$ 6000,00 a uma
taxa de juros compostos de 10% ao ano e saldou a divida da
seguinte maneira:
I) 2 anos após ter contraído a dívida, pagou R$ 2260,00;
II) 2 anos após o 1º pagamento, pagou mais R$ 3050,00;
III) 1 ano após o 2º pagamento, quitou a dívida.
Nessas condições, pode-se afirmar:
(01) Depois do primeiro pagamento, a pessoa ficou devendo
R$ 4340,00.
(02) Após o segundo pagamento, a dívida correspondia a 50%
do valor do empréstimo.
(04) No momento em que a pessoa quitou o empréstimo, a
dívida correspondia a R$ 3300,00.
(08) O montante pago pelo empréstimo foi igual a R$ 9000,00.
(16) O valor pago pelos juros da dívida correspondeu a 43,5%
do valor do empréstimo.
09. Um teatro colocou à venda ingressos para um espetáculo,
com três preços diferenciados de acordo com a localização da
poltrona. Esses ingressos, a depender do preço,
apresentavam cores distintas: azul, branco e vermelho.
Observando-se quatro pessoas na fila da bilheteria, constatouse o seguinte: a primeira comprou 2 ingressos azuis, 2
brancos e 1 vermelho e gastou R$ 160,00; a segunda
comprou 2 ingressos brancos e 3 vermelhos e gastou R$
184,00 e a terceira pessoa comprou 3 ingressos brancos e 2
vermelhos, gastando R$ 176,00. Sabendo-se que a quarta
pessoa comprou apenas 3 ingressos azuis, calcule, em reais,
quanto ela gastou.
(UFBA – 2002)
01. Considerando-se os números complexos z =
MATEMÁTICA – UFBA – 2001
QUESTÕES
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
01 + 02 + 16
01 + 04 + 08 + 16
01 + 04 + 08
02 + 16 + 32
02 + 04 + 16 + 32
02 + 04 + 08
01 + 02 + 08 + 16
02 + 04 + 16
-------------------------------------------------
i e
w = 1 + i, é correto afirmar:
(01)
z.w
=3
2
(02) w2 – 2z é um número real.
(04) z2 = 4(cos60º + isen60º)
(08)
z 1 i
=
w
2
(16) Se v = a + bi e v.w = 3i, então 2a + 4b = 9.
02. A partir de um quadrado Q1, com lado de medida l1,
constrói-se um quadrado Q2, de forma que seus vértices são
os pontos médios dos lados de Q1. Procedendo-se de modo
análogo, para cada n Є N, sendo n > 1, constrói-se um
quadrado Qn cujos vértices são os pontos médios dos lados de
Qn – 1, conforme ilustração abaixo.
Chamando-se de ln a medida do lado Qn, em u.c. e de
An a medida da área de Qn em u.a., é correto afirmar:
(01) (l1, l2, ..., ln, ...) é uma P.A de razão 1/2.
(02) (A1, A2, ..., An, ...) é uma P.G. de razão 1/2.
(04) Se l1 = 36, então l11 =
10. Um recipiente em forma de um cilindro circular reto, com
dimensões internas de 20 u.c. de diâmetro e 16 u.c. de altura,
está completamente cheio de argila que deverá ser toda
usada para moldar 10x bolinhas com 2 u.c. de raio. Calcule x.
3+
9
.
8
(08) O termo geral da seqüência (A1, A2, ..., An, ...) é
An = l12 . 21 – n .
(16) A soma infinita de (l1, l2, ..., ln, ...) é (2 +
(32) A soma dos 5 primeiros termos
(A1, A2, ..., An, ...), para A1 = 144, é 252.
2 )l1.
da
seqüência
03. Sendo as funções f: R→R e g: R – {1} → R – {2} definidas
GABARITO
19
29
13
50
54
14
27
22
84
154
pelas equações f(x) = x2 – 2x e g(x) =
2x
,
x 1
é correto
afirmar:
(01) Se x < -1, então g(x) > 0
(02) A equação f(x) = g(x) possui duas soluções distintas.
(04) A função composta fog satisfaz a equação
f(g(x)) =
4x
x 2x 1
2
para todo x
1.
(08) A função h, definida por h(x) = g(x + 1), é ímpar.
(16)
A
g-1(x) =
inversa
da
função
g
é
dada
pela
equação
x
.
x2
(08) A solução do sistema M.X
04. Dadas as funções f, g e h, definidas por f(x) =
2x,
x + y + z = 0.
(16) Existem a, b
g(x) = log5(x – x2) e h(x) = x3 + x2 – 1, é correto afirmar:
(32) Para todo k
(01) A figura abaixo representa um esboço do gráfico da
função q, definida por q(x) = f--1(x) + 2.
R ec
0
= 1
0
satisfaz a equação
R* tais que Mt = M.
0
0
R, o sistema P.X =
é possível e
determinado.
06. Considerando-se os pontos A = (-1, 0) e B = (2, 3) do
plano cartesiano, é correto afirmar:
(01) O ponto médio do segmento AB tem abscissa igual a 1/2
e ordenada igual a 3/2.
(02) O simétrico do segmento AB em relação ao eixo das
abscissas é o segmento AC, sendo C = (-2, -3).
(04) O perímetro do triângulo ABD, sendo D = (-2, 3), é, em
(02) O conjunto solução da inequação f(h(x)) < 1/2 é o
intervalo ]- , -1[.
(04) O resto da divisão do polinômio h(x) por x – 1 é igual a -3.
(08) O domínio da função g está contido no intervalo ]0, 2[.
(16) A equação g(x) = 1 possui uma única solução real.
(32) A equação g(x) =
log x . log (1 x )
log 5
é verdadeira para
todo x pertencente ao domínio de g.
(64) O número 1 é a única raiz real do polinômio
p(x) = h(x) – 1.
05.
Considerando-se
as
d
1 0 1
N = 2, P =
0 k 2
0
são números reais e c
matrizes
M
a 1 1
= b 1 1,
c 0 0
x
e X = y , em que a. b. c. d e k
z
0, pode-se afirmar:
(01) M é inversível, e a soma dos termos da primeira coluna
M-1 é igual 1, para quaisquer valores a, b R e c R*.
(02) O determinante da matriz 2M é igual a 4c.
(04) Se P.N =
3 / 2
3
, então d.k = .
4
1
u.c., um número real maior que 10.
(08) A equação y = -x + 1 representa uma reta que contém os
pontos A e B.
(16) A equação x2 + y2 + 2x – 17 = 0 representa uma
circunferência com centro em A, que passa pelo ponto B.
07. Na figura ao lado, cada quadrado representa um
quarteirão de um condomínio e, em cada cruzamento de ruas
indicado por um x, foi instalado um semáforo, exceto em A e
B. Um carro desloca-se de A até B, obedecendo as seguintes
condições:
- o trajeto deve ser formado por segmentos de reta ligando
pontos de cruzamentos consecutivos;
- cada segmento só pode ser percorrido num dos dois
sentidos indicados pelas setas na figura;
- o tempo gasto para percorrer cada segmento é de 2 minutos;
- cada semáforo, após ligado, funciona alternando apenas os
sinais verde e vermelho, que ficam acessos por períodos de 3
e 2 minutos, respectivamente;
- o carro pára em cada semáforo que estiver fechado e parte
no exato instante em que este abrir.
MATEMÁTICA – UFBA – 2002
Com base nessas informações, é correto afirmar:
(01) Existem 10 trajetos possíveis.
(02) Se os semáforos estiverem desligados, o tempo gasto
pelo carro através de qualquer dos caminhos possíveis é igual
a 8 minutos.
(04) Se os semáforos forem ligados ao mesmo tempo,e o
carro partir de A, no instante em que os semáforos abrirem,
serão gastos pelo menos 12 minutos no trajeto.
(08) Se os semáforos forem ligados de modo aleatório, então
o tempo gasto pelo carro será, no máximo, 18 minutos.
(16) Sendo constante a distancia entre dois cruzamentos
consecutivos quaisquer, então a distancia total percorrida pelo
carro dependerá do trajeto.
QUESTÕES
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
02 + 04 + 16
02 + 04 + 08+ 16
01 + 02 + 04
01 + 02 + 08 + 16
01 + 04 + 08 + 32
01 + 04 + 16
01 + 04 + 08
01 + 08 + 16
-------------------------------------------------
GABARITO
22
30
07
27
45
21
13
25
04
22
(UFBA – 2003)
08. A receita de uma empresa cresceu, durante o ano 2000, a
uma taxa constante de 1% ao mês. Sabendo-se que a receita
do mês de fevereiro foi de R$ 51.005,00, é correto afirmar:
(01) A receita do mês de março foi de R$ 51.515,00.
(02) A média da receita do primeiro trimestre foi de
R$ 51.005,00.
(04) A receita mediana do período de janeiro a abril foi de
R$ 51.515,05.
(08) O resultado da operação 510,05 x 10 4(1,0111 – 1)
representa a receita total, em reais, do período de fevereiro a
dezembro de 2000.
(16) A probabilidade de que a receita de um mês escolhido ao
acaso no ano de 2000 seja superior a R$ 51.005,00 é igual a
5/6.
09. Um tanque, na forma de um cilindro circular reto, deve ser
construído de modo que sua área lateral seja 24 u.a., e seu
volume seja igual ao de uma esfera cujo raio mede 3 u.c.
Calcule, em u.c., a altura desse tanque.
10. Numa faculdade, estudam 1000 alunos, sendo 500 de
Direito, 300 de Computação e 200, de Letras. Em cada um
dos três cursos, o custo médio mensal por aluno independe da
quantidade de alunos e é, respectivamente, igual a R$ 300,00,
R$ 400,00 e R$ 250,00.
Se a faculdade quiser aumentar o número de alunos de
Computação em 15% e o de Letras em 30%, sem alterar o
gasto total com os alunos, calcule, em porcentagem, qual
deverá ser a redução do número de alunos do curso de
Direito.
01. Considere as funções f: R+*
f(x) = log2 x e g(x) =
afirmar:
x3
R
e g: R→R definidas por
– 1. Nessas condições, é correto
(01) A função g é ímpar.
(02) A função g possui uma única raiz real.
(04) O ponto (1, 0) pertence à interseção dos gráficos de f e
de g.
(08) A imagem de x = 8 pela função composta g o f é igual a
3.
(16) A função composta g o f é inversível, e sua inversa
(g o f)-1 : R
R*
definida pela equação (g o f)-1 (x) =
2
3
x 1
.
02. Um cliente, ao solicitar um empréstimo de R$ 5000,00 a
determinado banco, foi informado de que, no vencimento, em t
meses, deveria pagar o valor calculado pela formula
P(t) = 5000(1,1)t. Nessas condições, é correto afirmar:
(01) A condição estipulada pelo banco corresponde a um
empréstimo com juros compostos de 10% ao mês.
(02) O valor dos juros a serem pagos, se o cliente optar pelo
prazo de 2 meses, corresponderá a 20% do valor emprestado.
(04) O valor total a ser pago, se o cliente optar pelo prazo de 3
meses, será igual a R$ 6655,00.
(08) A divida do cliente, se ele optar pelo prazo de 10 meses,
será maior que R$ 10000,00.
(16) P(1), P(2),..., nesta ordem, formam uma progressão
aritmética.
(32) A figura ao lado representa um esboço do gráfico da
função P(t), com t N*
05. Considere um plano , um ponto P
não contida em
e uma reta r
. Nessas condições, é correto afirmar:
(01) Toda reta que passa por P não intercepta r.
(02) Se r é paralela a alguma reta contida em
paralela a
, então ela é
.
(04) Se P r, então r é perpendicular a
.
(08) Existe um plano que contém r e é perpendicular a
(16) Se Q é um ponto não pertencente a
03. Considerando as funções f: R→R e g: R→R definidas
pelas equações f(x) = -x + 2 e g(x) = x2, é correto afirmar:
não está contida em
.
, então a reta PQ
.
(32) Qualquer reta perpendicular a r intercepta
.
(01) A soma das soluções da equação f(x) = g(x) é igual a -1.
(02) O trapézio ABCD, que tem como vértices A = (-2, 0),
B = (1, 0) e os pontos de interseção dos gráficos de f e de g,
tem área igual a 15/2 u.a.
(04) O conjunto solução da inequação g(x)
[1, + [.
(08) A desigualdade
f2(x)
f(x) é o intervalo
g(x) é válida para todo x
Considerando-se
o
sistema
de
R.
equações
1 2 k
x 2 y kz 1
S:
x y z 1 e as matrizes B = 1 1 1 ,
k 1 1
kx y z 0
C =
1
1
0
e X =
x
y ,
z
sendo k um número real, pode-se
(01) A matriz transposta de B.C é a matriz (1, 1, k – 1).
(02) A matriz inversa de B, para k = 0, é a matriz
2 2
1
.
1 1 1
1 1
1
B-1 =
(04) S é um sistema determinado, se k
1 e k 2.
(08) O terno (-1, 1, -1) é a única solução do sistema S, para
k = 0.
(16) O sistema S é possível e indeterminado, para k = 1.
0
0
0
(32) O conjunto solução do sistema homogêneo B.X = ,
sendo
o
polígono
A(1;3),
ABCDEFG
B(1;5),
no
1
;5 ,
2
C
plano
D(3;7),
11
;5 , F(5;5) e G(5;3), pode-se afirmar:
2
E
(01) A reta que passa pelos pontos A e F é paralela à reta que
passa pelos pontos C e D.
(02) A distância entre os pontos D e G é igual a
2 5 u.c.
(04) A reta que passa pelos pontos C e G tem coeficiente
angular negativo.
(08) O ponto de interseção das diagonais do retângulo ABFG
é (3;4).
(16) A área do polígono ABCDEFG é igual a 13 u.a.
(32) A figura abaixo representa o polígono obtido pela reflexão
de ABCDEFG em relação à origem.
afirmar:
para k = 1, é {(x, 0, -x), x
Considerando-se
cartesiano,
(16) A imagem da função h definida por h(x) = g(x) – f(x) é
[-9/4, + [.
04.
06.
R}.
07. Usualmente, chama-se Taxa de Analfabetismo de uma
localidade a taxa percentual de analfabetos com idade
superior a 10 anos, calculada em relação ao número de
habitantes, nessa faixa etária, da localidade. A tabela a seguir
contém dados sobre o Estado da Bahia e os municípios
baianos de Salvador e de Cel. João Sá.
09. Calcule o número de pares de vértices não consecutivos
que se pode obter num prisma triangular.
10. Uma ponte, com formato de um arco de circunferência e
comprimento igual a
Bahia
Salvador
Cel. João Sá
População com idade
superior a 10 anos
10405000
2030000
14748
Número de analfabetos
com idade superior a 10
anos
2247000
126000
7320
Taxa de Analfabetismo
21,6%
49,6%
4
3
quilômetros, liga dois pontos A e B
situados em margens opostas de um rio, conforme figura
abaixo. Sabe-se que O é o centro da circunferência e que o
ângulo AOB mede
2
3
rd. Calcule d2 , sendo d a distância,
em quilômetros, entre os pontos A e B.
Com base nessas informações, é correto afirmar:
(01) A taxa de analfabetismo de Salvador é de,
aproximadamente, 6,2%.
(02) Mais de 80% da população da Bahia com mais de 10
anos de idade não é habitante de Salvador.
(04) Na faixa etária considerada acima, o número de
analfabetos de Salvador corresponde a aproximadamente
5,6% do número de analfabetos da Bahia.
(08) Se o número de analfabetos de Cel. João Sá com idade
superior a 10 anos fosse 3660, a taxa de analfabetismo desse
município seria menor que a do Estado da Bahia.
(16) Escolhendo-se ao acaso um habitante do Estado da
Bahia, analfabeto, na faixa etária referida, a probabilidade de
que ele seja habitante de Cel. João Sá é maior do que a de
ser habitante de Salvador.
(32) Escolhendo-se ao acaso uma pessoa de Salvador ou de
Cel. João Sá, com idade superior a 10 anos, a probabilidade
de que essa pessoa seja analfabeta é maior que 27%.
MATEMÁTICA – UFBA – 2003
QUESTÕES
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
02 + 04 + 16
01 + 04 + 08
01 + 02 + 16
04 + 08 + 32
02 + 08 + 16
02 + 04 + 08 + 16 + 32
01 + 02 + 04
01 + 02 + 04 + 32
-------------------------------------------------
GABARITO
22
13
19
44
26
62
07
39
06
12
(UFBA – 2004)
08. O lucro de uma empresa, em função dos meses de janeiro
a dezembro do ano de 2001, é dado, em milhares de reais,
pela fórmula:
L(n) = 39n –
3n2,
n
{1, 2, ..., 12}
em que os números naturais n, variando de 1 a 12,
correspondem, respectivamente, aos meses de janeiro a
dezembro.
Com base nessas informações, pode-se afirmar:
(01) O maior lucro da empresa, no ano, ocorreu em junho e
em julho.
(02) O maior lucro obtido pela empresa, no ano, foi de
R$ 126000,00.
(04) O lucro, durante o segundo semestre, foi decrescente.
(08) O lucro foi igual nos meses de maio e setembro.
(16) O lucro médio, nos três primeiros meses, foi de
R$ 66000,00.
(32) O lucro mediano, nos doze meses, foi de
R$ 99000,00.
01. Considere as sentenças:
p: “ Todo país em desenvolvimento possui dívida externa ” ;
q: “ Todo país economicamente independente não possui
dívida externa “ ;
r: “ Nenhum país em desenvolvimento é economicamente
independente “ ; e os conjuntos
X = { países em desenvolvimento }
Y = { países que possuem dívida externa }
Z = { países economicamente independentes }
Nessas condições, pode-se afirmar:
(01) A negação da sentença p é: “ Algum país em
desenvolvimento não possui dívida externa “.
(02) “ Existe país economicamente independente que possui
dívida externa e nenhum país em desenvolvimento é
economicamente independente “ é equivalente a q r.
(04) p
(08) q
r ├-- q é válido.
r ├-- p não é válido.
(16) A representação em diagrama de Venn do argumento
p q ├-- r é
02. Sobre os números reais, é verdade afirmar:
(01) Se x = 0,666..., y = -1,333... e z = 12,444... então
z
x y
= 6,222....
(02) O valor da expressão
3
(5 2 6 )(5 2 6 ) é um
número irracional.
(04) Se x < 0, então
x2
= -x .
(08) Dividindo-se o número 34 em partes inversamente
proporcionais a 1, 2 e 5, obtêm-se os valores x, y e z,
respectivamente, tais que 3yz = 5x.
(16) Se em uma progressão aritmética de sete termos, a soma
é igual 133, então o termo médio é igual a 19.
(32) A equação (x – 1)2 = x – 1 possui duas raízes distintas.
03. Considerando-se as funções f, g e h, com domínio R,
definidas pelas equações f(x) = x – 2, g(x) = x2 – x – 2 e
h(x) = 3x, pode-se afirmar:
f ( x)
1
, para todo x R.
g ( x) x 1
(02) Se x1, x2 R, as tais que g(x1) = g(x2), então x1 = x2 ou
04. Um aparelho eletro domestico está à venda pelo preço de
R$ 300,00, numa loja que oferece as seguintes opções de
pagamento:
Plano A: à vista, com 5% de desconto;
Plano B: pagamento no prazo de um mês, sem desconto nem
acréscimo;
Plano C: pagamento no prazo de dois meses, com juros
compostos de 5% ao mês.
Uma segunda loja vende o mesmo aparelho por um preço de
5% mais caro que a anterior, mas oferece um desconto de
10% à vista.
Com base nessas informações, é correto afirmar que, se um
cliente
(01) optar pelo plano B, pagará 5% a mais que outro que optar
pelo plano A.
(02) preferir o pagamento à vista, será mais vantajoso comprar
na segunda loja.
(04) optar pelo plano C, pagará um valor maior que R$ 330,50.
(08) aplicar, no dia da compra, a uma taxa de 7% ao mês, o
dinheiro que usaria para o pagamento à vista no plano A, após
dois meses terá o suficiente para o pagamento do valor
correspondente ao plano C.
(16) comprar dois aparelhos à vista, um em cada loja, a média
dos preços dos aparelhos será inferior a R$ 285,00.
(01)
x1 + x2 = 1.
(04) A imagem da função composta g o f, é o intervalo
[-9/4, + [.
05. Considerando-se os pontos A(1;2), B(-1;4) e C(2;7) no
plano cartesiano, é válido afirmar:
(08) O gráfico da g o f pode ser obtido a partir do gráfico de g,
transladando-o duas unidades para a direita.
(16) A função composta h o g: R R+* é crescente.
(01) Se A, B, C e D são, nessa ordem, vértices consecutivos
de um retângulo, então o produto das coordenadas de D é 20.
(02) A área do triângulo ABC é igual a 6 u.a.
(04) O ponto médio do segmento BD pertence à reta y = x +
21/5.
abaixo representa um esboço do gráfico da sua inversa.
(08) A circunferência de centro
(32) A função composta h o f: R R+* é bijetora e a figura
circunscrita ao retângulo ABCD.
3 9
; e
2 2
raio
26
2
está
(16) O coeficiente da reta angular da reta AC é positivo.
(32) O simétrico do segmento AB, em relação ao eixo Oy, está
contido no 2º quadrante.
06. Uma empresa de microcomputadores vende alguns
produtos em pacotes, de acordo com a tabela a seguir:
Monitor
(unidade)
Processador
(unidade)
Gravador
(unidade)
Preço
(R$)
Pacote1
2
1
3
2736
Pacote2
1
0
2
840
Pacote3
1
2
0
2952
Com base nos dados acima e considerando-se que o preço
unitário de cada produto independe do pacote, pode-se
afirmar:
(01) A soma dos preços de uma unidade de cada produto é
um múltiplo de 8.
(02) É possível que o preço de um monitor seja menor que R$
300,00.
(04) O preço do gravador é maior que R$ 420,00.
(08) Se o preço de um monitor é igual a R$ 400,00, então a
soma dos preços unitários de cada um dos outros produtos é
um número divisível por 5.
(16) Se A é a matriz 2 x 3, formada com as duas primeiras
linhas e as três primeiras colunas
da tabela, e B é a matriz 3 x 2, formada com as três linhas e
8 8
.
4 5
as duas primeiras colunas, então A.B =
07. Defini-se a População Economicamente Ativa (PEA) de
uma região como o número de indivíduos com idade igual ou
superior a dez anos, enquadrados numa das situações
Ocupado ou Desempregado. A taxa de Desemprego total é
então definidas como a razão (expressa em termos
percentuais) entre o número de desempregados e a PEA. A
taxa de Desemprego Total na Região Metropolitana de
Salvador (RMS), no mês de maio de 2003, foi de
aproximadamente 30%. Com base nessas informações, é
correto afirmar:
(01) Sabendo-se que, no mês de maio de 2003, a PEA foi
estimada em 1662000, o número estimado de desempregados
situa-se entre 490000 e 500000.
(02) Mais de 2/3 dos indivíduos do PEA são classificados
como ocupados.
(04) Se a PEA representa y% da população da RMS, o
contingente de desempregados, no mês de maio de 2003,
corresponde a 0,3y% da população da RMS.
(08) Se no mês de junho de 2003, não houver variação na
PEA e a taxa de desemprego total diminuir meio ponto
percentual (passado para, aproximadamente, 29,5%), haverá
um acréscimo aproximado de 8310 pessoas ocupadas com
mais de dez anos de idade.
(16) Sabendo-se que a Taxa de Desemprego Total e a PEA
(aproximadas), referentes ao mês de abril, foram 29% e
1645000, respectivamente, pode-se estimar em 5500 o
aumento do número de desempregados em maio, com relação
a abril.
08. Uma escola de Ensino Médio – com 20 alunos na primeira
série, 30 alunos na segunda e 40 na terceira – organiza um
torneio de tênis. Na primeira fase, cada aluno jogará duas
partidas contra dois adversários distintos escolhidos de acordo
com as seguintes regras que levam em consideração a série
que está cursando e sua média escolar, comparada com a
média de cada um dos demais alunos da escola:
- para o primeiro adversário, um aluno com média escolar
superior à sua;
- para segundo adversário, outro aluno que esteja cursando a
sua mesma série, ou outra mais adiantada.
Fica excluído dessas regras apenas o único aluno que obteve
a maior media escolar. Este aluno, que cursa a terceira série,
poderá escolher livremente seus adversários. Classifica-se
para a segunda fase cada aluno que vencer as duas partidas
disputadas.
Considerando-se que não há a possibilidade de empate no
jogo de tênis, que a probabilidade de um aluno ganhar de
outro da mesma serie é igual a 1/2, e a de ganhar de outro de
série mais avançada é igual a 1/3, é correto afirmar que, se o
aluno
(01) com a segunda maior média está na terceira série, então
ele pode escolher seus adversários de 38 maneiras distintas.
(02) com a segunda maior média está na terceira série, sua
probabilidade de classificação é igual a 1/4.
(04) com a segunda maior média está na segunda série, então
ele pode escolher seus adversários de 69 maneiras distintas.
(08) com a segunda maior média está na segunda série,
então, a depender de sua escolha, sua probabilidade de
classificação é igual a 1/6 ou a 1/9.
(16)tem a menor média em relação a todos os demais e está
na primeira série, então ele pode escolher seus adversários de
7835 maneiras distintas.
09.
Considere a figura acima em que
- a distância entre as retas r e s é igual a 20 u.c.;
- os segmentos AB e CD medem, respectivamente, 10 u.c. e
30 u.c.;
- P é o ponto de interseção dos segmentos AD e BC.
Com base nesses dados, calcule a área do triângulo APB, em
u.a..
10. Uma empresa fabrica copos plásticos para refrigerante e
café. Os copos têm a forma de tronco de cone e são
semelhantes, isto é, um deles pode ser obtido a partir do outro
por homotetia. O copo de refrigerante mede 9,5cm de altura e
tem capacidade para 480ml. Sabendo-se que o copo de café
tem 3,8cm de altura, determine a sua capacidade em mililitros,
aproximando o resultado para o número inteiro mais próximo.
MATEMÁTICA – UFBA – 2004
QUESTÕES
PROPOSIÇÕES
CORRETAS
01 + 08 + 16
01 + 04 + 16 + 32
02 + 04 + 08
02 + 04 + 16
01 + 02 + 08 + 16
01 + 02 + 16
ANULADA
01 + 02 + 08
-------------------------------------------------
01
02
03
04
05
06
07
08
09
10
03. Considere um empréstimo de um capital de R$2 000,00 a
uma taxa mensal de 10%.
Nessas condições, é correto afirmar:
(01) Se for considerada a capitalização simples, o montante
F(n), expresso em reais, ao final de n meses, será dado por
F(n) = 2000 (1+10n).
(02) Ao final de dois meses, o valor dos juros na capitalização
composta será igual a R$420,00.
(04) Na capitalização composta, o montante G, expresso em
reais e dado em função do número n de meses, pode ser
representado pelo gráfico abaixo.
GABARITO
25
53
14
22
27
19
ANULADA
11
25
31
(08) Se for considerada a capitalização composta, a seqüência
dos montantes mensais será uma progressão geométrica de
razão 1,1.
(16) Se a capitalização for composta, o capital dobrará de
valor ao final de
log 2
log 1,1
meses.
(UFBA – 2005)
01. Sobre os números reais, é correto afirmar:
04. Considerando-se as funções f, g : R→R, tais que
(01) Se x e y são positivos, então
x<
y se e somente se
f(x) = -3x2 +
3 x + 5 e g(x) = px + q, sendo p R* e q R, é
x < y, x > 1 e y > 1.
(02) Se x e y são números racionais que representam,
respectivamente, a medida do raio da base e a altura de um
cilindro circular reto, expressos em u. c., então o volume do
cilindro, expressos em u.v., é um número irracional.
(04) Se x e y são inteiros positivos impares consecutivos e
correto afirmar:
x.y = 1295, então x e y são números primos.
(08) Para cada n N, 2n + 5 – 3 é um número primo.
(04) Se a composta f o g for uma função quadrática, seu
gráfico terá concavidade voltada para cima.
(08) Existe p R* tal que a função composta f o g é inversível.
(16) Se a > 0, então a equação x4 – a2 = 0 possui, no máximo,
duas soluções reais distintas.
(01) A função f é crescente no intervalo ]- ,
(02) Existe p R tal que o gráfico da função h: R→R, dada por
h(x) = f(x) + g(x), é simétrico em relação ao eixo das
ordenadas, qualquer que seja q R.
(16) G1 = g, G2 = g o g, G3 = g o g o g, ... são funções afins,
cujos os coeficientes angulares formam uma progressão
geométrica de razão p, e o coeficiente linear da função G n é
02. Considerando-se a seqüência de números reais dada por
2n 8
.an – 1
17 n
igual a q
2
a0 = 1 e a n =
Para
n N * , é correto afirmar:
(01) Todos os termos da seqüência são positivos.
(02) Para qualquer n N, an é um número racional.
(04) (a1, a2, a3, ...) é uma progressão geométrica.
(08) Para, n N*, an > an – 1 se, e somente se, n > 8.
(16) Existe n N*, tal que an = n.an – 1.
3 / 6 ].
pn 1
.
p 1
05. Considerando-se, no plano cartesiano com origem O, os
pontos A(5, 0), B(5,
2 3 ) e C(-2, -2 3 ), é correto afirmar:
(32) Escolhendo-se ao acaso um par de sapatos de número
38, a probabilidade de que ele seja do modelo masculino é
igual a
(01) O coeficiente angular da reta que passa por A e C é igual
a
2 3
.
3
(02) A área do quadrilátero OABC é igual a 6
1
.
10
07.
3 u.a.
(04) Existe uma única função quadrática cujo gráfico passa
pelos pontos O, B e C.
(08) O segmento obtido através do segmento OC, aplicando a
rotação de 30º no sentido anti-horário em torno da origem,
está contido no eixo das ordenadas.
(16) Os triângulos OCD e ABC são semelhantes, sendo D o
ponto de interseção do segmento BC com o eixo das
ordenadas.
06. Uma empresa fabrica apenas dois modelos de sapato,
sendo um feminino e outro masculino. Os modelos femininos
são fabricados nos números 35, 36, 37 e 38, e cada par é
vendido por R$ 80,00. Os modelos masculinos são fabricados
nos números 38, 39, 40 e 41, e o preço de venda de cada par
é R$ 100,00. Os gráficos abaixo mostram as quantidades (em
milhares de pares) produzidas e vendidas por mês pela
fabrica.
Considerando-se
u 2 log v 0
B =
0
2w
u 2 log v 0
a
matriz
u 2 log v
0
sendo u, w R e v R+*,
u 2 log v
é correto afirmar:
(01) A matriz B é simétrica, para quaisquer u, w R e v
R+*.
(02) O determinante de B é negativo se e somente se u o e
v >1.
(04) Se u = 6, e v = 0,0001, então existe um único w Î R tal
que os elementos da diagonal principal de B são medidas de
um triângulo eqüilátero.
(08) Se u = 0, existem v R+* e w R tais que B2 é uma
matriz nula.
(16) Para qualquer w R, o sistema de equações BX = 0 tem
x
uma infinidade de soluções X = y , se e somente se v = 1.
z
08. Na figura, os quadrados ABCD e A’B’C’D’, cujos lados
medem 10 u.c., são bases de um prisma reto de altura igual a
5
3 u.c.,
e o ponto O é, ao mesmo tempo, o centro do
quadrado ABCD e o vértice da pirâmide com base A’B’C’D’. A
partir dessas informações, pode-se afirmar:
Com base nessas informações, é correto afirmar:
(01) O preço de venda médio dos sapatos é igual a R$ 88,00.
(02) O preço de venda mediano dos sapatos é igual a
R$ 80,00.
(04) A receita obtida com a venda de sapatos masculinos
representa menos de 82% da receita correspondente ao
modelo feminino.
(08) Se a venda do modelo feminino for reduzida em 20%, os
dois modelos passarão a contribuir com o mesmo montante
para receita da empresa.
(16) Escolhendo-se ao acaso um par de sapatos, entre todos
os produzidos em um mês, a probabilidade de que ele seja de
um número 38 ou do modelo feminino é igual a
16
.
25
(01) Qualquer plano que contenha uma face lateral da
pirâmide faz um ângulo de 60º com o plano da base A’B’C’D’.
(02) Qualquer aresta lateral da pirâmide faz um ângulo de 60º
com o plano da base A’B’C’D’.
(04) Existem uma aresta da pirâmide que é coplanar ao
segmento DD’ e uma aresta da pirâmide que está contida
numa reta reversa à reta que contém DD’.
(08) A área do triângulo OC’D’ é igual a 50 u.a.
(16) O volume do sólido compreendido entre o prisma e a
pirâmide é igual a
500 3
u.v.
3
09. Durante uma reunião, ocorreu uma divergência
quanto à formação de uma comissão gestora, a ser
escolhida pelos presentes. Um grupo defendia uma
comissão com três membros, sendo um presidente, um
vice-presidente e um secretário. Outro grupo queria uma
comissão com três membros sem cargos definidos. A
primeira alternativa oferece 280 possibilidades de
escolha a mais que a segunda.
Determine o número de pessoas presentes à reunião,
sabendo-se que esse número é maior que 5.
MATEMÁTICA – UFBA – 2005
QUESTÕES
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
02 + 16
01 + 02 + 08
02 + 08 + 16
01 + 02 + 16
04 + 08
01 + 02 + 16
01 + 04
01 + 04 + 08
-------------------------------------------------
GABARITO
18
11
26
19
12
19
05
13
08
12
(UFBA – 2006)
01. Com base nos conhecimentos sobre geometria plana, é
correto afirmar:
10. Considere um triângulo eqüilátero cujos lados medem
2( 3 1) u.c.
e três circunferências com raios medindo
( 3 1) u.c., cada uma delas com centro em um vértice do
triângulo, conforme a figura. Considere então um segundo
triângulo T satisfazendo as seguintes condições:
(01) Se dois triângulos semelhantes têm a mesma altura
relativa a um lado comum, então eles são congruentes.
(02) Se dois triângulos semelhantes têm a mesma área, então
eles são congruentes.
(04) Em um triângulo eqüilátero, o ângulo agudo formado pela
altura relativa a um lado e a mediana relativa a outro lado
mede 60º.
(08) Em um paralelogramo, se dois lados formam um ângulo
- as três circunferências estão contidas no interior do triângulo
T;
3 cm, então a menor diagonal
de 150º e medem 1cm e
mede 1cm.
(16) Se A é um conjunto formado por n pontos coplanares de
modo que três pontos quaisquer de A não são colineares,
então o número de triângulos que se pode formar com vértices
-cada vértice do
circunferências;
pertencentes a A é igual a
triângulo
T tangencia duas
dessas
- cada vértice do triângulo T pertence à mediatriz de um dos
lados do triângulo inicial.
Com base nesses dados, determine, em u.c., o perímetro do
triângulo T.
n(n 1)( n 2)
.
6
02. O trabalho de crianças e adolescentes é um problema que
afeta principalmente os paises mais pobres sendo motivo de
preocupação de governantes e de organismos internacionais,
Com base nos dados obtidos na Pesquisa Nacional de
Amostra por Domicílios (PNAD/IBGE) em 2003, existiam, no
Brasil, 43,05 milhoes de pessoas na faixa etária de 5 a 17
anos das quais 5,07 milhoes estavam ocupadas (trabalhando),
o que corresponde a 11,78% dessa população. A tabela a
seguir apresenta esses dados por regiões do Brasil.
Regiões do Brasil
Norte
Nordeste
Centro-Oeste
Sudeste
Sul
Faixa etária de 5 a 17 anos
População
Percentual
(em milhões)
de pessoas
ocupadas %
2,98
9,51
13,81
15,30
3,12
9,75
17,05
8,63
6,09
14,43
Com base nessas informações sobre a faixa etária de 5 a 17
anos, é correto afirmar:
05. Considerando-se, no plano cartesiano, a reta r
(01) Mais de 50% das pessoas nessa faixa etária
encontravam-se nas regiões Sul e Sudeste.
(02) O número de pessoas ocupadas, nessa faixa, era menor
na região Sudeste do que na região Sul.
(04) Entre as pessoas ocupadas nessa faixa etária
aproximadamente 10% encontravam-se na região CentroOeste.
(08) Escolhendo-se ao acaso uma pessoa da região Norte
nessa faixa etária, a probabilidade de que ela não esteja
ocupada é igual a 90,49%.
(16) Supondo-se um crescimento de 1% ao ano para a
população da faixa etária de 5 a 17 anos, a estimativa é de
que , no ano de 2006 a população dessa faixa seja de
43,05x1,030301 milhoes de pessoas.
(5;0) e raio 5
03. Considerando-se C1, C2, C3,... cilindros com mesmo
volume, de modo que os respectivos raios das bases,
medindo em cm, formem uma P.G. com primeiro termo e
razão iguais a
5 , é correto afirmar:
5 é o termo de ordem 122 da
(01) O número real
seqüência dos raios.
(02) O termo geral da seqüência dos raios pode ser escrito
561
representada pela equação y = 15 e a circunferência de centro
3 , pode-se afirmar:
(01) A circunferência intercepta o eixo y nos pontos (0; 5
e (0; -5
3)
3).
(02) Existe um único triângulo eqüilátero cujos vértices são o
centro da circunferência e dois pontos da reta r.
(04) A circunferência pode ser representada pela equação
x2 – 10x + y2 = 50.
(08) Existe uma única reta que passa pelo ponto (10; 0) e é
tangente á circunferência.
(16) A imagem da reta r pela rotação de 60º no sentido antihorário, em torno do ponto (5,15), intercepta a circunferência
em dois pontos distintos.
(32) Existe um número natural k tal que a imagem da
circunferência pela homotetia de razão
8
7
k
e o centro na
origem é uma circunferência que intercepta a reta r em dois
pontos distintos.
k
como rk = 5 2 .
(04) Considerando-se apenas os termos de ordem par da
seqüência dos raios, obtém-se uma P.G. de razão 5, em que
todos os termos são positivos.
(08) A seqüência formada pelas alturas dos cilindros é uma
P.G. de razão 1/5.
(16) Sendo o volume dos cilindros igual a 20 cm3, a área
total do primeiro cilindro expressa em cm2, é um número
menor que 42.
04. Com relação às funções f, g:R→R e h:]0, + [ R,
dadas por f(x) = bx + b-x, g(x) = bx – b-x + x e
h(x) =
logbx, sendo b um número real positivo e diferente de 1, é
correto afirmar:
(01) O gráfico da função f é simétrico em ralação à origem.
(02) A função produto fg é ímpar se, e somente se, b ]0, 1[.
(04) A função composta f o h é dada por f(h(x)) =
(08) x R, f(x)(g(x) – x) = g(2x) – 2x.
(16) Existe b ]0, + [ - { 1 } tal f(2) = 2.
x2 1
.
x
(32) Existe b ]0, + [ - {1} tal que h(x + y) = h(x)h(y) para
quaisquer números reais positivos x e y.
06. O custo de produção diária e a receita pela venda de um
determinado produto fabricado por uma empresa, em milhares
de reais, são dados, respectivamente, pelas funções
C: [0, + [ [0, + [ e R: [0, + [ [0, + [, com
C(x) = 2 + log2(x + 1) e R(x) = 2x – 1, sendo x o número de
centenas de unidades produzidas. Com base nessas
informações, é correto afirmar:
(01) As funções C e R são crescentes.
(02) R é a função inversa de C.
(04) Para uma receita igual a R$ 7000,00, custo é igual a R$
4000,00.
(08) Se a produção é de 100 unidades, então um aumento de
200% na produção acarretará um aumento de 100% no custo.
(16) A função lucro, definida por L = R – C, satisfaz a condição
L(0) = L(1), mas não é uma função constante.
(32) A figura abaixo ao lado representa um esboço do gráfico
da função C.
07. Os estoques de gasolina, álcool e diesel de três postos de
combustíveis são dados, em milhares de litros, na tabela a
seguir, sendo c e k números reais
não-negativos.
Posto 1
Posto 2
Posto 3
Gasolina
2
1
c
Álcool
1
4
k
Diesel
1
K
1
Seja M a matriz formada pelos estoques de cada combustível
em cada posto, na mesma disposição da tabela dada. Sabese que o preço por litro de cada combustível é o mesmo nos
três postos. Com base nessas informações, é correto afirmar:
(01) Se c =1, então a matriz M2 é simétrica.
(02) Se c =1, então a matriz M é inversível, para todo
k [0, + [.
(04) Se c = 3, então existe k [0, + [ para o qual o
determinante da matriz M é nulo.
(08) Conhecendo-se os preços por litro de álcool e de diesel e
sabendo-se que o primeiro é maior que o segundo, então
existe k [0, + [ tal que a soma dos valores dos estoques
desses dois combustíveis,
no Posto 2, é igual à
mesma soma no Posto 3.
(16) Assumindo-se que c = 3, k = 0 e que as somas dos
valores dos estoques dos Postos 1, 2 e 3 são,
respectivamente, R$8 800,00, R$10 800,00 e R$9 600,00,
então a soma dos preços, por litro, de cada combustível é
igual a R$6,00.
- cada time ganharia dois pontos por vitória e um ponto por
empate, não marcando ponto em caso de derrota;
- ao final das seis partidas,em que estará em disputa um total
de 12 pontos, o campeão seria o time que acumulasse o maior
número de pontos.
Um dos times somou três pontos nas partidas realizadas no
próprio estádio, e outro empatou todas as partidas que
disputou. Sabendo que, ao final de todas as partidas, os times
ficaram com pontuações distintas e que a pontuação do
campeonato foi um número par, determine o produto das
pontuações finais dos três times.
10. Uma senhora teve um filho a cada dois anos, exceto no
terceiro parto quando nasceram duas crianças. Sabendo que
todos os filhos estão vivos e que após o nascimento do último,
em qualquer época, o número de filhos vezes a idade dos
gêmeos é igual à soma das idades de cada um. Determine o
número de filhos que essa senhora teve.
MATEMÁTICA – UFBA – 2006
QUESTÕES
08. Com relação a um prisma reto de base quadrada, é
correto afirmar:
(01) Cada diagonal de uma face divide-a em dois triângulos
congruentes.
(02) Existem exatamente 8 segmentos que ligam pares de
vértices não pertencentes a uma mesma face.
(04) Dadas duas faces não adjacentes e quatro vértices, dois
em cada uma dessas faces, existe um plano que contém
esses quatro vértices.
(08) Dados dois vértices consecutivos, para n {1, 3, 5, 7}
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
02 + 04 + 08 + 16
08 + 16
02 + 04 + 08
04 + 08
02 + 04 + 16 + 32
01 + 04 + 16 + 32
01 + 08 + 16
01 + 08 + 16 + 32
-------------------------------------------------
existe um caminho poligonal que liga esses vértices e é
formado por n arestas, cada uma percorrida uma única vez.
(UFBA – 2007)
(16) Se a medida do lado da base e a altura do prisma são
números inteiros consecutivos, e o volume é um número primo
p, então p é único.
(32) Existem exatamente 24 pirâmides distintas cujas bases
são faces do prisma e cujos vértices são também vértices do
prisma.
01. Sobre os números reais, é correto afirmar:
09. Numa disputa entre três times, estabeleceu-se que:
- cada time jogaria duas vezes contra os outros dois, sendo
uma partida no seu próprio estádio e outra no estádio do
adversário;
GABARITO
30
24
14
12
54
53
25
57
48
06
(01) Se a é o maior número de três algarismos divisível por 7,
então a soma de seus algarismos é igual a 22.
(02) Se a é um múltiplo de 3, e b é um múltiplo de 4, então a.b
é múltiplo de 6.
(04) Se c = a + b e b é divisor de a, então c é múltiplo de a.
(08) Se a e b são números reais tais que |a| ≤ b, então b é
positivo.
(16) Para quaisquer números a e b, |a – b| ≤ |a + b|.
(32) Dados quaisquer números reais a, b e c, se a ≤ b, então
a.c ≤ b.c
02. Um comerciante compra determinado produto para
revender. A diferença entre o preço de venda e o preço de
custo, quando positiva, é chamada de “lucro por unidade”. O
comerciante estabeleceu um preço de venda tal que o seu
lucro seja 50% do preço de custo.
Com base nessas informações, é correto afirmar:
(16) Se a função quadrática h(x) = ax2 + 4x + c admite máximo
1 no ponto de abscissa -2, então c – a = 4.
(32) Se a função real f(x) = ax4 + bx2 + c, com a ≠ 0, possui
apenas duas raízes reais positivas distintas, entre duas raízes,
então a função quadrática g(x) = ax2 + bx + c possui duas
raízes reais positivas distintas.
(01) O lucro total obtido é diretamente proporcional à
quantidade vendida.
(02) O preço de venda é 150% maior que o preço de custo.
(04) Se o comerciante conceder um desconto de 20% sobre o
preço de venda, então terá um lucro de 20% sobre o preço de
custo.
(08) Se o preço de custo aumentar em 10% e o preço de
venda for mantido, então o lucro será 40% do preço de custo
04. A vitamina C é hidrossolúvel, e seu aproveitamento pelo
organismo humano é limitado pela capacidade de absorção
intestinal, sendo o excesso de ingestão eliminado pelos rins.
Supondo-se que, para doses diárias inferiores a 100mg de
vitamina C, a quantidade absorvida seja igual à quantidade
ingerida e que, para doses diárias maiores ou iguais a 100mg,
a absorção seja sempre igual à capacidade máxima do
organismo – que é de 100mg -, pode-se afirmar, sobre a
ingestão diária de vitamina C, que são verdadeiras as
proposições
após o aumento.
(16) Se o comerciante fizer uma promoção do tipo “Leve 4
unidades e pague apenas 3”, então isso representara, para o
cliente, um desconto total de 25%.
(32) Se, nos meses de janeiro e fevereiro de 2006, o lucro do
comerciante cresceu exponencialmente a uma taxa mensal de
2% em relação ao mês anterior, então, ao final de fevereiro, o
lucro foi de 4,04% maior que o lucro ao final de dezembro de
2005.
03. Com base nos conhecimentos sobre funções, é correto
afirmar:
(01) Se a função afim m(x) = ax + b, a ≠ 0, é crescente, então
a > 0 ou x > -
(01) Para a ingestão de até 100mg, a quantidade absorvida é
diretamente proporcional à quantidade ingerida.
(02) Para a ingestão acima de 100mg, quanto maior for a
ingestão, menor será a porcentagem absorvida de vitamina
ingerida.
(04) se uma pessoa ingere 80mg em um dia e 120mg no dia
seguinte, então a media diária da quantidade absorvida
nesses dois dias foi de 100mg.
(08) A razão entre a quantidade ingerida e a quantidade
absorvida pelo organismo é igual a 1.
(16) A função f que representa a quantidade de vitamina C
absorvida pelo organismo, em função da quantidade ingerida
x, é dada por f(x) =
x, se 0 x 100
100, se x 100
(32) O gráfico abaixo representa a quantidade de vitamina C
absorvida pelo organismo em função da quantidade que foi
ingerida.
b
.
a
(02) Se a função afim p(x) = ax + b, a ≠ 0, é decrescente,
então a função é negativa para todo x < -
b
.
a
(04) Se a função quadrática n(x) = ax2 + bx + c é par,
então
b = 0.
(08) Se a figura representada um esforço do gráfico da função
quadrática r(x) = ax2 + bx + c, então b é um numero real
negativo.
05. Considerando-se as funções f(x) = x – 2 e g(x) = 2x,,
definidas para todo x real, e a função h (x) = log 3 x, definida
para todo x real positivo, é correto afirmar:
(01) O domínio da função
g
h
é o conjunto dos números reais
positivos.
(02) A função
f .h
fog
se anula em dois pontos.
(04) A função composta hog é uma função linear.
(08) O gráfico da função hof intercepta o eixo Ox em um único
ponto.
(16) O gráfico da função fog intercepta o gráfico de h(x) no
ponto de abscissa igual a 1.
(32) Se g(h(a)) = 8 e h(g(2b)) = log3 8, então
a
b
= 18.
(01) Se duas matrizes quadradas de mesma ordem, A e B,
são simétricas, então a matriz (A + B) também é simétrica.
x 2
1 x
é inversível, então x é um número
racional.
(04) Se x é um número real não nulo e
x2
0
x2
1
1
3
1
x 1
x
7
2
x
1
= a, então
x y b
2 x ay 3
, então 2 < x < 3.
(32) Se P(x, y) é o ponto de interseção das medianas do
é impossível, então
.
08. Com base nos conhecimentos sobre geometria espacial,
pode-se afirmar:
(01) Se uma reta r e um plano são paralelos, então toda
reta perpendicular à reta r é também perpendicular ao plano
.
(02) Se um ponto P não pertence a uma reta s, então existe
um único plano passando por P, paralelo à reta s.
(04) Se uma reta r está contida em um plano , e a reta s é
reversa a r, então a reta s intercepta o plano .
(08) Se
e
são dois planos perpendiculares, e r é uma
reta perpendicular a
, que não está contida em , então r
09. Na figura ao lado, todos os triângulos são retângulos
isósceles, e ABCD é um quadrado.
Nessas condições, determine o quociente
(16) O sistema linear
(a 1) x (a 1) y b
(a 1) x (a 1) y c
11
.
3
é paralela a .
(16) Se dois planos são perpendiculares, então toda reta de
um deles é perpendicular ao outro.
(32) Três planos distintos interceptam-se segundo uma reta ou
um ponto.
= a3.
(08) Se o sistema linear
b–a≠
x
x 1
DC
AB
triângulo ABC, sendo B(2, 3) e C(4, 1), então x + y =
06. Com base nos conhecimentos sobre matrizes,
determinantes e sistemas lineares, é correto afirmar:
(02) Se a matriz
(16) Se x =
GH
CE
.
é possível e
determinado, quaisquer que sejam os valores reais a, b e c.
(32) Existe um número real a, não nulo, tal que o sistema
linear homogêneo
x ay z 0
2 x ay 3z 0
admite uma única
solução.
10. Considerando que os números reais a, b e c formam,
nessa ordem, uma progressão geométrica e satisfazem a
07. Considerando-se um triângulo retângulo isósceles ABC,
ˆ C , que mede
um ponto D tal que AD BD e o ângulo DB
150º, representados na figura, é correto afirmar:
igualdade log2 a +
1
log b 2
+ 2log4 c = 9, determine o valor de
b.
MATEMÁTICA – UFBA – 2007
QUESTÕES
(01) O quadrilátero ADBC é um trapézio.
(02) O triângulo ADB é eqüilátero.
(04) O ângulo
CAˆ D mede 105º.
(08) A área do quadrilátero ADBC é igual a
AB
4
2
(
3 +2).
01
02
03
04
05
06
07
08
09
10
PROPOSIÇÕES
CORRETAS
01 + 02
01 + 04 + 16 + 32
01 + 04 + 08 + 16 +32
01 + 02 + 16
04 + 08 + 16 + 32
01 + 04 + 08 + 16
02 + 04 + 08 + 32
08
-------------------------------------------------
GABARITO
03
53
61
19
60
29
46
08
04
08