interação entre a luz clássica e a matéria quântica

CENTRO UNIVERSITÁRIO DA FEI
HENRIQUE LANZA FARIA TORRES
INTERAÇÃO ENTRE A LUZ CLÁSSICA E A MATÉRIA QUÂNTICA
São Bernardo do Campo
2010
HENRIQUE LANZA FARIA TORRES
INTERAÇÃO ENTRE A LUZ CLÁSSICA E A MATÉRIA QUÂNTICA
Relatório Final de Projeto de Iniciação Científica,
apresentado ao Centro Universitário da FEI,
como requisito fundamental para a apresentação
dos resultados do presente projeto de pesquisa,
orientado pelo Prof. Dr. Roberto Baginski Batista
Santos.
São Bernardo do Campo
2010
A mente que se abre a uma nova idéia jamais voltará ao seu tamanho original.
Albert Einstein
RESUMO
A interação entre a luz e a matéria é um dos ramos de estudo da Física Quântica mais
amplos. Um de seus processos fundamentais é a absorção e a emissão de luz que serve como
base tanto para tecnologias de informação quântica quanto para a computação, comunicação e
a criptografia quânticas. Sendo assim, a compreensão correta da interação entre a radiação e a
matéria é importante para a fundamentação e o desenvolvimento de aplicações tecnológicas
como a geração e a detecção de laser e a transmissão de informação por lasers em fibras
ópticas. O objetivo do presente projeto é modelar e descrever como um átomo se comporta
quando está interagindo com um feixe de laser. O átomo será modelado como um sistema de
dois níveis e o feixe de laser será modelado como um estado coerente de luz, pois envolve um
grande número de fótons. A interação entre o átomo e a luz será descrita pelo modelo de
Jaynes-Cummings, no qual um fóton é retirado do campo de luz sempre que o átomo é
excitado e um fóton é acrescido ao campo de luz quando o átomo realiza uma transição para
seu estado de menor energia.
Palavras-chave: Física Quântica. Átomos. Fótons. Modelo de Jaynes-Cummings.
SUMÁRIO
1 OBJETIVO .............................................................................................................................................. 6
2 REVISÃO BIBLIOGRÁFICA ...................................................................................................................... 6
2.1 Introdução ao formalismo e aos postulados da física quântica .................................................... 7
2.1.1 Postulado 1: estados físicos e vetores ................................................................................... 8
2.1.2 Postulado 2: observáveis e operadores ................................................................................. 9
2.1.3 Postulado 3: medições e autovalores .................................................................................. 10
2.1.4 Postulado 4: valores médios e probabilidades .................................................................... 13
2.1.5 Postulado 5: evolução temporal .......................................................................................... 15
2.1.6 O Quadro da Interação ......................................................................................................... 16
2.2 Sistemas quânticos de dois níveis: um modelo simples para o átomo ....................................... 18
2.2.1 A evolução temporal dos operadores atômicos .................................................................. 21
2.3 Oscilador harmônico: a descrição quântica da luz ...................................................................... 22
2.3.1 A evolução temporal dos operadores de criação e aniquilação de fótons .......................... 24
2.4 Modelo de Jaynes-Cummings: a interação entre átomos e fótons ............................................ 25
2.4.1 A evolução temporal do hamiltoniano de interação ........................................................... 29
2.5 Estados coerentes de luz ............................................................................................................. 31
3 METODOLOGIA................................................................................................................................... 33
4 RESULTADOS ...................................................................................................................................... 36
4.1 Estados vestidos e emaranhamento quântico ............................................................................ 36
4.2 Probabilidade de transição e as oscilações de Rabi .................................................................... 38
4.3 Inversão da população e número de fótons ............................................................................... 41
4.4 O operador densidade................................................................................................................. 43
4.5 Colapsos e revivais quânticos...................................................................................................... 44
5 CONCLUSÃO ....................................................................................................................................... 50
6 REFERÊNCIAS BIBLIOGRÁFICAS .......................................................................................................... 51
1 OBJETIVO
O objetivo do projeto é a descrição detalhada da evolução temporal de um sistema
atômico simples, tratado como um sistema de dois níveis, em interação com a luz de um laser,
tratada como um campo eletromagnético quantizado em um estado coerente de radiação.
Este relatório apresenta uma descrição detalhada da evolução temporal de um sistema
atômico em interação com um campo eletromagnético quantizado em um estado de Fock, no
qual há um número definido de fótons. Serão obtidos os autoestados do sistema bem como
suas respectivas energias. As oscilações de Rabi para a probabilidade de transição do átomo
serão deduzidas e comparadas com resultados experimentais da literatura.
Em seguida, serão introduzidos os estados coerentes da radiação e algumas de suas
propriedades para que possamos obter a evolução temporal do sistema e descrever os
fenômenos de colapsos e revivais quânticos, comparando-os com resultados empíricos
também encontrados na literatura.
2 REVISÃO BIBLIOGRÁFICA
Na teoria da interação da luz com a matéria, supõe-se que o átomo possa ser descrito
por um sistema de dois níveis e que a luz do laser possa ser representada por um único modo
de campo eletromagnético com N fótons. A esse estado damos o nome de estado de Fock da
luz.
Por
sua
vez,
estados
de
Fock
puros
são
muito
difíceis
de
produzir
experimentalmente[1,2]. Na maior parte das vezes, a luz é adequadamente representada como
um estado coerente, também conhecido como estado clássico[3,4]. Um estado coerente, no qual
a fase do campo eletromagnético é bem definida, é a descrição quântica mais próxima
possível da chamada luz clássica. Em um estado coerente, o número de fótons presentes no
feixe de luz não é uma grandeza bem definida.
6
Nesta seção, vamos inicialmente revisar os postulados da física quântica, aproveitando
a oportunidade para introduzir o formalismo abstrato de Dirac no chamado quadro de
Schrödinger, em que os estados físicos evoluem no tempo enquanto a maior parte dos
operadores não evolui no tempo. Em seguida, vamos apresentar os principais resultados
relacionados a sistemas de dois níveis e osciladores harmônicos, que serão usados como
modelos para um átomo e para o campo eletromagnético, respectivamente. Introduziremos o
quadro da interação (ou quadro de Dirac), no qual tanto os vetores de estado quanto os
operadores dependem do tempo. Apresentaremos uma descrição detalhada do modelo de
Jaynes-Cummings para a interação entre átomos e fótons e, finalmente, definiremos os
estados coerentes e revisaremos algumas de suas propriedades.
2.1 Introdução ao formalismo e aos postulados da física quântica
Nesta seção, faremos uma revisão dos cinco postulados da física quântica, essenciais
para o desenvolvimento deste trabalho. Os postulados explicam como
i.
descrever o estado físico de um sistema quântico por meio de vetores em um
espaço vetorial abstrato;
ii.
descrever as grandezas físicas observáveis por meio de operadores neste
espaço vetorial;
iii.
extrair os valores possíveis das grandezas físicas na forma dos autovalores dos
operadores que as representam;
iv.
atribuir probabilidades de observação a cada um dos valores possíveis da
medição de uma grandeza física;
v.
computar a evolução temporal do estado físico do sistema quântico.
Nesta revisão, faremos uso do formalismo abstrato introduzido por Dirac[5] para a
física quântica. Este formalismo mostrou-se bastante conveniente para o estudo da interação
de um átomo com um modo do campo eletromagnético por permitir que os detalhes
específicos do sistema fossem especificados à medida que o trabalho se desenvolvia.
7
2.1.1 Postulado 1: estados físicos e vetores
Na física quântica, átomos e seus estados físicos são representados por vetores em
espaços vetoriais abstratos conhecidos por espaços de Hilbert.
Um espaço de Hilbert é um espaço vetorial dotado de produto interno, ou seja, com
noções de distância e ângulos, de dimensão finita ou infinita definida sobre os complexos.
Esse espaço obedece a uma relação de completude e permite que, de certa forma, noções
intuitivas sejam aplicadas em espaços funcionais[6]. Esta estrutura algébrica é a linguagem
matemática natural para o desenvolvimento da física quântica.
Em mecânica quântica, o estado de um sistema físico é descrito por um vetor de estado
(ket)
em um espaço de Hilbert complexo. Os vetores de estado armazenam toda a
informação disponível sobre o sistema.
Partindo-se do princípio da superposição, o vetor de estado
, pode ser escrito como
combinação linear dos vetores da base do espaço de Hilbert
(1)
Os kets definem os vetores de estado existentes no espaço de Hilbert, porém
paralelamente também existe o espaço dual definido pelos seus próprios vetores de estado,
conhecidos como bras
, de forma que para todo ket
existe um bra
em seu espaço
dual correspondente [7].
Partindo-se desta correspondência dual CD temos:
,
(2)
e se
(3)
então
(4)
8
Tendo conhecimento destes princípios, podemos introduzir o conceito de produto
interno entre os vetores |
e|
como
(5)
isto é, como sendo a ação do bra
associado ao ket
sempre um número complexo que depende de
sobre o ket
e o resultado é
.
Define-se também como norma do vetor
a seguinte propriedade:
(6)
e dois vetores não nulos são ortogonais apenas se
(7)
Outro ponto importante a se destacar, é que tanto o vetor
quanto o vetor
(onde c é um número complexo não nulo) representam o mesmo estado físico. Desta forma,
exige-se que todos os vetores obedeçam a condição de normalização
(8)
A condição de normalização é de extrema importância, pois está associada à
interpretação probabilística da física quântica.
2.1.2 Postulado 2: observáveis e operadores
Uma grandeza observável, como o próprio nome já diz, é uma grandeza que pode ser
mensurada e necessita ter como valor um número real. O segundo postulado afirma que todo
observável é representado por um operador linear hermitiano.
Matematicamente, um operador é um ente que estabelece uma relação funcional entre
dois espaços vetoriais. A relação funcional que um operador estabelece pode ser chamada de
transformação linear. Na mecânica quântica os operadores são utilizados para representar
grandezas físicas. Um operador  que representa o observável A atua sobre o ket
pelo
lado esquerdo produzindo um novo ket
(9)
9
Ao exigir que o operador seja linear, estamos apenas preservando o caráter lienar das
operações sobre os vetores do espaço de Hilbert,
(10)
Para compreender o que significa para um operador ser hermitiano, é preciso
introduzir a noção de adjunto hermitiano ou, simplesmente, adjunto
do operador Â. O
operador ajunto é definido por meio da correspondência dual. Assim como a operação
produz o ket
o bra
, o operador adjunto é aquele que atuando sobre o bra
pela direita produz
, isto é,
(11)
Deve-se notar que enquanto um operador atua sobre um ket pela esquerda, sua ação
sobre o bra é realizada pela direita.
Finalmente, um operador é hermitiano se
(12)
.
Neste caso, ainda podemos dizer que o operador é autoadjunto visto que
.
Operadores hermitianos possuem duas propriedades que são úteis para a física quântica. A
primeira propriedade estabelece que os autovalores de um operador hermitiano são sempre
reais enquanto a segunda afirma que os autovetores de um operador hermitiano formam uma
base ortogonal para o espaço de Hilbert.
2.1.3 Postulado 3: medições e autovalores
O terceiro postulado afirma que os resultados possíveis para a medição do observável
A no estado físico
são os autovalores
medição é descrito pelo autovetor
Um autovetor
de . Neste caso, o estado do sistema após a
associado ao autovalor
associado a um autovalor
.
do operador
é um vetor que satisfaz
(13)
10
Como operadores hermitianos possuem sempre autovalores reais, fica claro por qual
motivo os observáveis devem ser representados por deles. Além disso, operadores
hermitianos possuem autovetores que formam uma base de vetores ortonormais para o espaço
de Hilbert. Assim, podemos expandir qualquer vetor em termos dos N autovetores
de um operador hermitiano Â,
(14)
Neste caso, dizemos que
Para determinar os coeficientes
é uma superposição dos autovetores
.
da expansão, basta notar que como os autovetores de  são
ortonormais,
(15)
então,
(16)
isto é, o coeficiente
é apenas projeção do vetor de estado de estado
sobre o vetor
da
base. Esta relação permite que escrevamos
(17)
e definimos uma representação para o operador identidade Î em termos dos autovetores de
qualquer operador hermitiano Â
(18)
Como
e
, o produto
interno
(19)
entre estes vetores pode ser interpretado como o produto de matrizes
11
(20)
Esta identificação sugere a chamada representação matricial na qual o ket
é representado na base dos autovetores de  pela matriz coluna
(21)
e o bra
é, por sua vez, representado pela matriz linha
(22)
Em outras palavras, o bra
é representado por uma matriz que é a conjugada
complexa da transposta da matriz que representa o ket
representar matricialmente um operador
que se
. De modo semelhante, podemos
na base dos autovetores de Â. Para tal, basta notar
, então
(23)
na qual
é o coeficiente da expansão de
e o elemento de matriz do operador
entre os autovetores do operador  é
(24)
Deste modo, o operador
pode ser representado na base dos N autovetores de  como
(25)
Já a representação do operador  na base de seus autovetores tem uma característica
especial. Como
, a representação matricial de  é diagonal e os elementos da
diagonal são os autovalores de Â,
.
(26)
12
Na
representação
matricial,
operadores
sempre
serão
matrizes
quadradas.
Aproveitando-se que foi introduzido o conceito de representação matricial dos operadores
hermitianos, podemos introduzir agora a noção de comutador. O comutador
operadores  e
entre os
é definido por
(27)
Os observáveis A e B são compatíveis se o comutador
. Neste caso, é
possível medir simultaneamente tanto o observável A quanto o B, isto é, os autovetores do
operador  são também autovetores do operador
. Por outro lado, se
, é possível
mostrar que[7]
(28)
na qual
é a dispersão ou variância do observável A
em torno do valor médio
A como
. Comumente define-se a incerteza
na medição do observável
.
A equação (28) é o enunciado matemático geral do princípio de incerteza de
Heisenberg. O que o princípio de incerteza afirma é que certos pares de observáveis não
podem ter ambos valores bem definidos, isto é, incerteza nula, em um dado estado físico. Do
ponto de vista físico, a incompatibilidade entre observáveis é uma das novidades trazidas pela
física quântica. Do ponto de vista formal, contudo, a ausência de comutatividade do produto
de matrizes é a regra geral. Isso significa que a maior parte dos observáveis não devem ser
compatíveis entre si, isto é, não podem ser medidos simultaneamente com incerteza nula.
2.1.4 Postulado 4: valores médios e probabilidades
No quarto postulado, temos que o valor médio das medições do observável A em um
sistema físico descrito pelo vetor de estado
é
(29)
13
Se expandirmos o vetor de estado
ortonormais
como uma superposição dos autovetores
do operador  que representa o observável A,
(30)
obteremos
(31)
pois
(32)
Como os únicos valores possíveis para o observável A são seus autovalores
, podemos interpretar a equação (32) como uma sugestão de que a
probabilidade de obter o autovalor
descrito por
em uma medição do observável A em um sistema físico
é
(33)
O número complexo
é a amplitude de probabilidade de obter
medição de A em um sistema no estado
em uma
. A amplitude de probabilidade é muito importante
na física quântica. Se
e se
então a probabilidade
da transição entre os estados
,
e
é dada por
(34)
O termo
é responsável pela interferência entre estados classicamente
distinguíveis.
14
2.1.5 Postulado 5: evolução temporal
O postulado 5 afirma que o ket
que descreve o estado físico do sistema no
instante de tempo t se relaciona com o ket
de tempo
que descreve o estado do sistema no instante
por
(35)
e o operador de evolução temporal obedece a equação de Schrödinger
(36)
Ĥ
Equivalentemente, podemos escrever a equação de Schrödinger para o ket
como
(37)
Ĥ
Em qualquer uma das versões da equação de Schrödinger, o operador hamiltoniano Ĥ
representa o observável energia, que é a única grandeza física mencionada explicitamente nos
postulados da física quântica.
No caso simples em que Ĥ não depende explicitamente do tempo,
(38)
Ĥ
Como o operador hamiltoniano é hermitiano, há um conjunto de autovetores
, os
autoestados da energia, que satisfazem Hˆ Ei  Ei Ei e que formam uma base para o espaço
de Hilbert. Neste caso, podemos expandir o estado inicial
em termos dos autoestados
da energia,
(39)
para descobrir que
(40)
15
O valor médio do observável
é, então,
(41)
o que mostra que o valor médio é constituído por termos que oscilam no tempo na frequência
(42)
No caso particular em que
é um autoestado da energia, o valor médio de
se torna
(43)
que é uma grandeza independente do tempo. Por este motivo, os autoestados da energia são
chamados estados estacionários.
2.1.6 O Quadro da Interação
Todos os postulados introduzidos e discutidos até o presente momento consideram o
operador de evolução temporal afetando somente os vetores de estado. Nesta formulação, os
operadores não participam da dinâmica do sistema. Essa abordagem da mecânica quântica é
conhecida como quadro ou representação de Schrödinger[7].
Há, contudo, duas abordagens alternativas ao quadro de Schrödinger, os quadros de
Heisenberg e da interação ou de Dirac. No quadro de Heisenberg, são os operadores que
evoluem no tempo enquanto os vetores de estado permanecem constantes. Esta abordagem
realça o paralelismo formal entre a mecânica clássica e a mecânica quântica sugerindo uma
interpretação[5] em que a física quântica é uma física clássica em que variáveis dinâmicas
foram substituídas por operadores e em que o colchete de Poisson
pelo comutador
foi substituído
.
Já o quadro da interação é uma forma intermediária entre os quadros de Schrödinger e
Heisenberg, no qual a interação física entre as partes de um sistema é destacada. No quadro da
interação, tanto operadores quanto vetores de estado evoluem no tempo. Porém, enquanto os
operadores evoluem segundo uma dinâmica regida pelo hamiltoniano livre, não interagente,
16
os vetores de estado evoluem segundo uma dinâmica regida pelo hamiltoniano de interação. O
quadro da interação torna-se interessante por facilitar os cálculos em problemas nos quais os
termos de interação do hamiltoniano dependem explicitamente do tempo.
A fim de definir melhor o quadro da interação, considere um hamiltoniano
no
quadro de Schrödinger. Este hamiltoniano pode ser dividido em uma componente livre
e
outra com dependência explícita do tempo
que representa a interação:
(44)
Ainda que a divisão do hamiltoniano seja bastante arbitrária, é uma boa prática
escolher para
a parte do hamiltoniano total que não deve depender do tempo e deixar
todos os termos que podem apresentar dependência temporal para
. Deste modo, os
operadores, que obedecem uma álgebra difícil, não comutativa, evoluem de modo mais
simples enquanto a parte mais difícil da evolução temporal pode ser deixada para os vetores
de estado.
No quadro da interação, os vetores de estado
são novamente definidos como
transformações dos estados de Schrödinger. Estes vetores de estado são transformados apenas
pela parte livre do hamiltoniano:
(45)
onde
(46)
de forma semelhante podemos obter as transformações para os operadores:
(47)
É interessante notar que o operador evolução temporal livre comuta com seu operador
adjunto, ou seja:
(48)
17
A partir destas propriedades, obtemos a equação de Schrödinger (evolução temporal
dos estados) no quadro da interação como sendo:
(49)
e, consequentemente, a equação de Heisenberg (evolução temporal dos operadores) será:
(50)
Podemos concluir que no quadro de Dirac a evolução temporal dos estados é
determinada somente pelo termo de interação do hamiltoniano do sistema. Em contrapartida,
a evolução temporal dos operadores neste quadro é controlada pelo componente livre do
hamiltoniano.
Havendo descrito o formalismo básico da física quântica, passamos ao estudo da
interação entre o átomo e o campo eletromagnético. No projeto, o átomo foi descrito como um
sistema de dois níveis análogo a uma partícula de spin 1/2 enquanto o campo eletromagnético
foi tratado como um conjunto de osciladores harmônicos quânticos distribuídos por todos os
pontos do espaço. Nesta representação, a quantização da energia surge naturalmente e leva à
introdução do conceito de fóton, o quantum de luz.
2.2 Sistemas quânticos de dois níveis: um modelo simples para o átomo
Sistemas de dois níveis são importantes na física quântica porque, na maior parte das
vezes, apenas dois níveis estão envolvidos em transições radiativas, isto é, transições que
envolvem a absorção ou a emissão de um fóton de energia bem definida. Desta forma, é
conveniente representar um sistema atômico ou molecular complexo em interação com fótons
de energia bem definida por apenas os dois níveis envolvidos na transição, descartando os
demais, que não estão diretamente envolvidos.
A construção de um sistema de dois níveis segue o modelo de uma partícula de spin ½,
como o elétron. Podemos aproximar o átomo de dois níveis por um spin pois o fóton que faz a
18
primeira transição não possui energia suficiente para as transições posteriores e, na maior
parte das vezes, os átomos decaem para o estado fundamental antes de serem capazes de
absorver outro fóton.
Neste caso, os autoestados do sistema de dois níveis são denotados por
e
(“e”
correspondendo a excited e “g” correspondendo a ground, que representam respectivamente
os estados excitado e fundamental do átomo de dois níveis) e são autovetores do operador de
Pauli
(51)
associados aos autovalores +1 e -1, respectivamente. Os outros operadores de Pauli podem ser
representados, na base dos autovetores de
, como
(52)
e
(53)
Estes operadores, representam as rotações do spin em um espaço abstrato de duas
dimensões, por isso todos são descritos por matrizes de ordem 2. Vale lembrar que esta
representação dos operadores de Pauli foi realizada no quadro de Schrödinger. No quadro de
Heisenberg, os operadores de Pauli podem evoluir no tempo, dependendo da escolha que
fizermos para o hamiltoniano livre
.
O conjunto dos três operadores de Pauli obedece à álgebra do momento angular
expressa na relação de comutação[7]
(54)
na qual
é o símbolo antissimétrico de Levi-Civita[6]. Isso mostra que os operadores de
Pauli são observáveis incompatíveis, isto é, não existe um estado físico que seja,
simultaneamente, autovetor de
precisamente os valores de
,
,
e
e
. Em outras palavras, não é possível conhecer
ao mesmo tempo.
Podemos escrever o hamiltoniano para um sistema de dois níveis não interagente
como
19
(55)
Ĥ
de tal modo que
Ĥ
(56)
Ĥ
É conveniente introduzir operadores não hermitianos que realizam transições entre os
dois níveis do sistema. Neste caso, o operador
(57)
responde pela transição do estado
para o estado
enquanto o operador
(58)
é responsável pela transição do estado
para o estado
.
Para analisar a influência destes operadores sobre um sistema de dois níveis devemos
considerar o sistema em uma superposição como
, onde
e
assumem valores entre 0 e 1 e representam, respectivamente, as probabilidades do átomo ser
encontrado ou no estado excitado ou no fundamental. Vamos utilizar também a representação
matricial para os estados
e
,
.
(59)
Há duas situações particulares interessantes. Considerando o átomo no estado
fundamental (
e
)
(60)
e
(61)
Vemos que se o átomo estiver inicialmente no estado fundamental, a ação de
corresponde a uma excitação atômica enquanto
aniquila o estado pois não há um nível de
20
energia abaixo do fundamental. Por outro lado, se o átomo estiver no estado excitado (
e
)
(62)
e
.
Neste caso, o operador
(63)
desexcita o átomo enquanto o operador
aniquila o estado
pois, por hipótese, não há um nível de energia acima do excitado que seja acessível. A
visualização correta do papel destes operadores para um sistema de dois níveis é essencial
para o desenvolvimento deste projeto.
2.2.1 A evolução temporal dos operadores atômicos
Vimos na seção 2.1.6 que tanto os vetores de estado quanto os operadores que
descrevem observáveis físicos de um sistema podem evoluir no tempo no quadro da interação.
Por esse motivo, torna-se interessante neste momento descrever como os operadores atômicos
,
e
se comportam na análise temporal do quadro de Dirac. Este resultado se mostrará
importante quando calcularmos a evolução temporal da função de onda que sistematiza a
interação de um átomo com um estado coerente de luz.
Já sabemos que a evolução temporal de um operador no quadro da interação é descrita
pela equação de Heisenberg. Fazendo a escolha
para que o hamiltoniano
livre não dependa explicitamente do tempo, a aplicação da equação (50) para o operador
,
nos leva a
(64)
pois
equação,
uma vez que o operador não depende explicitamente do tempo. Nesta
é o próprio operador
do quadro de Schrödinger (
) e, portanto, suas
propriedades já são bem conhecidas. De modo semelhante,
(65)
21
com
.
Por fim, a partir da mesma análise é possível observar que a derivada do operador
no tempo é nula, o que nos leva a concluir que este operador não evolui no tempo. Assim,
(66)
Este resultado é interessante e confirma que, como o operador de Pauli
permanece
o mesmo tanto no quadro de Schrödinger como no quadro de Dirac, o hamiltoniano atômico
para o sistema de dois níveis também se mantém inalterado em ambas as representações.
2.3 Oscilador harmônico: a descrição quântica da luz
O campo de radiação eletromagnética pode ser descrito como uma grande coleção de
osciladores harmônicos[8,9,10]. O hamiltoniano de um oscilador harmônico de massa m e
frequência angular
em uma dimensão é
Ĥ
p̂
x̂
(67)
Esse é o operador que representa a energia do sistema e podemos claramente observar
os termos referentes à energia cinética e à energia potencial através dos operadores de posição
x̂ e de momento linear p̂ respectivamente, que satisfazem a relação de comutação
(68)
x̂ p̂
É conveniente introduzir dois operadores não hermitianos
x̂
p̂
x̂
p̂
(69)
chamados operadores de aniquilação e de criação, respectivamente. Estes operadores
satisfazem a relação de comutação
(70)
e podem ser usados para definir o operador número
22
Ĥ
N̂
cujos autovetores, os estados de número
(71)
, satisfazem
(72)
N̂
Como Ĥ e N̂ comutam, os autovalores n de N̂ representam o número de excitações
da energia do oscilador e a aplicação dos operadores de aniquilação e de criação em um
estado de número
resulta em
(73)
justificando seus nomes pois o operador
operador
aniquila uma excitação do oscilador enquanto o
cria uma excitação no oscilador. A partir do estado fundamental
é possível
obter todos os autovetores pela aplicação repetida do operador de criação, isto é,
(74)
Os estados de número
, autovetores de N̂ , são também autoestados da energia.
Deste modo,
Ĥ
N̂
(75)
e o espectro de energia do oscilador harmônico é facilmente obtido em termos dos autovalores
n do operador N̂ ,
(76)
A representação do campo eletromagnético em termos de osciladores harmônicos
permite escrever o campo elétrico como[11]
(77)
na qual
e
são operadores de aniquilação e de criação de fótons no modo espacial
determinado pela função
que, por sua vez, é solução da equação de onda[8,9,10]
23
 2 
 2u k  2k u k  0
c
(78)

Deve-se notar que o índice k representa tanto o vetor k de propagação de onda quanto

as duas possíveis polarizações (   1 ou 2) ortogonais a k .
Em termos dos operadores
e
, o hamiltoniano do campo eletromagnético é
N̂
Ĥ
(79)
e o espectro de energia
(80)
pode ser interpretado como a soma das energias
Um estado
com
de
fótons em cada modo k do campo.
fótons em um dado modo do campo é, por analogia com o oscilador
harmônico, chamado estado de número.
Esta interpretação dá origem à chamada representação de Fock para a luz. Em um
estado de Fock
(81)
o número de fótons e, portanto, a intensidade da luz em cada modo são grandezas bem
definidas. Já a amplitude e a fase do campo não são grandezas bem definidas em um estado de
Fock. Pode-se dizer que um estado de Fock
é a representação mais pura da natureza
corpuscular da luz. Todavia, é extremamente difícil produzir estados de Fock[12,13].
2.3.1 A evolução temporal dos operadores de criação e aniquilação de fótons
Na seção 2.2.1, utilizamos a equação de Heisenberg para calcular a evolução temporal
dos operadores atômicos
,
e
. Podemos utilizar a mesma equação para o cálculo da
evolução temporal dos operadores de criação
e de aniquilação
de fótons. Este resultado
será utilizado em conjunto com a análise temporal dos operadores atômicos no cálculo da
evolução temporal do sistema interagente átomo mais estado coerente de luz.
24
A aplicação da equação de Heisenberg ao operador de aniquilação
nos fornece como
resultado
(82)
pois
uma vez que o operador não depende explicitamente do tempo. Nesta
equação,
é o próprio operador
do quadro de Schrödinger (
) e, portanto, suas
propriedades já são bem conhecidas. De modo semelhante,
(83)
com
.
Neste caso, podemos concluir que
(84)
o que significa que o operador de número de fótons
permanece o mesmo tanto no
quadro de Schrödinger como no quadro de Dirac. Assim, o hamiltoniano que representa o
oscilador harmônico para a descrição quântica da luz também se mantém inalterado em ambas
as representações.
2.4 Modelo de Jaynes-Cummings: a interação entre átomos e fótons
O modelo de Jaynes-Cummings descreve a interação entre um átomo de dois níveis e
um modo de campo eletromagnético quantizado, formado por uma determinada frequência,
uma certa polarização e uma direção de propagação.
Para o projeto, consideramos a existência de um campo eletromagnético confinado
dentro de uma cavidade, como mostrado na figura 1, no regime de acoplamento forte onde
haveria a interação com o átomo de dois níveis. No regime de acoplamento forte, a
probabilidade de se perder fótons por emissão espontânea em direção à lateral aberta da
cavidade ou por transmissão através dos espelhos é pequena e, portanto, os fótons têm
aumentada a probabilidade de interagir com o átomo.
25
Figura 1: Representação de um átomo e do campo eletromagnético no centro de uma cavidade isolada.
A interação de um sistema atômico de dois níveis com um único modo de campo
eletromagnético é usualmente descrita pelo hamiltoniano ressonante de Jaynes-Cummings[14]
Ĥ
no qual Ĥ
Ĥ
Ĥ
é o hamiltoniano referente ao átomo, Ĥ
eletromagnético ou radiação e Ĥ
(85)
Ĥ
é o hamiltoniano referente ao campo
é o hamiltoniano de energia que surge a partir da
interação átomo-radiação.
O hamiltoniano para o sistema de dois níveis não interagente é:
(86)
Ĥ
e o hamiltoniano para um único modo de campo eletromagnético pode ser escrito como:
Ĥ
N̂
(87)
A interação entre átomo e campo pode ser descrita pelo hamiltoniano de interação
entre um dipolo elétrico e o campo elétrico,
Ĥ
onde
(88)
é o campo elétrico, que por simplicidade, pode ser escrito como
26
(89)
e
(90)
é o momento de dipolo elétrico, operador responsável pelas transições atômicas.
É conveniente também neste momento introduzir o conceito da constante de
acoplamento entre o momento de dipolo elétrico (sistema atômico) e a amplitude do campo
elétrico (luz), também conhecida como frequência de Rabi
(91)
onde
é a amplitude do campo elétrico definida como
(92)
O hamiltoniano de interação nos leva a quatro processos diferentes, ilustrados na
figura 2. No modelo de Jaynes-Cummings, o hamiltoniano de interação consiste de dois
termos com interpretação física simples. O termo
representa a absorção de luz na qual um
fóton é aniquilado do campo de radiação enquanto o átomo realiza uma transição para o
estado de maior energia e o termo
representa a emissão de luz na qual um fóton é
emitido enquanto o átomo realiza uma transição para o estado de menor energia. Já os outros
dois processos não conservam o número de excitações do sistema (número de fótons mais
número de átomos no estado excitado) ou, se
, não conservam a energia do sistema.
Figura 2: Processos associados ao hamiltoniano de interação átomo-radiação.
27
Descartando os processos que não conservam a energia, em uma aproximação
conhecida por aproximação da onda girante, o hamiltoniano de interação se reduz a
(93)
Ĥ
Por fim, o hamiltoniano de Jaynes-Cummings será, na aproximação da onda girante,
Ĥ
Ĥ
Ĥ
(94)
Ĥ
Figura 3: Energia e processos envolvidos na interação dentro da cavidade.
A figura 3 mostra cada uma das partes do sistema, bem como a interação entre elas e
suas energias. Nesta figura,
ou dessintonia
é a diferença de energia entre o átomo e o campo. O detuning
pode ser escrito como
(95)
A situação em que
, é conhecido como caso de ressonância, e é quando a
excitação do átomo pode acontecer com maior facilidade. Para os outros casos (
), a
probabilidade de transição é menor.
O hamiltoniano de Jaynes-Cummings também pode ser escrito na forma matricial para
o caso com n fótons na cavidade como
Ĥ
(96)
28
proveniente do espaço dos estados da base, gerados pelos processos
e
que foram
mantidos, conhecidos como estados desacoplados:


correspondendo ao átomo excitado e n fótons na cavidade;
correspondendo ao átomo no estado fundamental e consequentemente a
geração de mais 1 fóton na cavidade.
Porém, podemos observar que os termos
da diagonal secundária são
diferentes de zero, o que mostra que a base desacoplada não é a ideal, pois nesta base, a
energia do sistema não é bem definida.
Um caso particular, que por facilidade algébrica, será comumente tratado neste projeto
é o caso em que temos um número definido de fótons na cavidade, que por sua vez, também
formarão a base vetorial utilizada em cálculos posteriores. Este caso é:
1. Quando temos 1 fóton na cavidade e o átomo está no estado de menor energia,
formando o vetor da base
;
2. Quando não há fótons na cavidade, pois o mesmo foi utilizado no processo de
excitação do átomo, formando o vetor da base
.
Para esta situação, o hamiltoniano total de interação se resume a:
(97)
Ĥ
2.4.1 A evolução temporal do hamiltoniano de interação
Quando introduzimos o conceito de quadro de Dirac ou da interação, explicamos a
necessidade da divisão do hamiltoniano
em duas componentes
(98)
Essa seleção, apesar de ser arbitrária, pode ser melhor executada escolhendo-se para
a parte do hamiltoniano total que não dependa do tempo e deixando todos os termos que
podem apresentar dependência temporal para
.
29
Aplicando-se esse conceito ao hamiltoniano de Jaynes-Cummings, podemos então
escolher
(99)
pois como vimos,
e
permanecem os mesmos tanto para o quadro de Schrödinger
quanto para o quadro da interação por não apresentarem dependência explícita no tempo.
Consequentemente,
(100)
é a parte do hamiltoniano de Jaynes-Cummings que pode, ao menos em princípio, sofrer
alguma variação temporal.
O objetivo desta seção é descobrir a forma do hamiltoniano de interação
no
quadro da interação. Este resultado é importante, pois segundo a equação de Schrödinger, a
evolução temporal de um estado coerente depende explicitamente do hamiltoniano de
interação no quadro de Dirac.
O hamiltoniano de interação no quadro de Dirac pode ser definido como
(101)
Substituindo pelos valores de
,
,
e
encontrados respectivamente nas
seções 2.2.1 e 2.3.1, temos
(102)
em que, novamente,
é a dessintonia entre as frequências características da
transição atômica e do laser. Por fim, podemos facilmente notar que no caso de ressonância,
, o hamiltoniano de interação é o mesmo tanto para o quadro de Dirac
quanto para o de Schrödinger
(103)
o que deve facilitar os cálculos, já que o hamiltoniano de interação entre átomo e radiação
para o quadro de Schrödinger já foi amplamente utilizado.
30
2.5 Estados coerentes de luz
Até o presente momento, a luz foi tratada como um campo eletromagnético quantizado
em um estado de Fock. Os estados de Fock são caracterizados por apresentarem um número
definido de fótons e, portanto, a intensidade da luz em cada modo também é uma grandeza
bem definida, o que já não acontece com a amplitude e a fase do campo eletromagnético.
Porém, sabemos que a representação da luz pelos estados de Fock não é a mais adequada
devido ao fato de que o número de partículas de um sistema quântico nem sempre é bem
definido, sendo possível que, ao se fazer diversas medições do número de fótons presentes em
um feixe de laser, sejam obtidos resultados diferentes a cada medição.
Neste contexto, a melhor representação possível na física quântica para descrever a luz
gerada por uma fonte clássica, com amplitude e fase bem definidas, são os estados coerentes
de luz. Os estados coerentes são uma superposição dos estados de Fock e por isso não
possuem um número bem definido de fótons[3],[8],[11].
Um estado coerente é definido como
(104)
onde
é denominado operador deslocamento e sua aplicação sobre o estado de vácuo
gera o estado coerente
. Podemos observar claramente que um estado coerente é uma
superposição de estados com todos os números de fótons possíveis, desde o estado de vácuo
com zero fótons até estados com número arbitrariamente grande de fótons.
O operador deslocamento é por sua vez, definido como
(105)
e é responsável pela transformação de um estado coerente atual para outro estado coerente,
dentro do espaço de fase óptico. O espaço de fase óptico é um espaço de fase em que todos os
estados quânticos de um sistema são descritos. Os espaços de fase dão origem aos diagramas
de fase, que são ferramentas utilizadas para se descobrir propriedades e comportamentos de
um sistema quântico que não podem ser obtidos de uma outra maneira imediata.
31
Para se entender a representação física associada ao parâmetro
, é interessante o
resultado obtido durante o cálculo da média do número de fótons em um estado coerente
:
(106)
isto é, o quadrado do módulo de
representa a média do número de fótons em um estado
coerente de luz.
Podemos facilmente demonstrar também que um estado coerente é um autoestado do
operador de aniquilação
(107)
e como o operador de aniquilação não é hermitiano, seus autovalores
não são
necessariamente números reais. A partir da equação (107) observamos que aniquilar um fóton
de um estado coerente não altera o número médio de fótons, pois o sistema ainda é descrito
pelo mesmo estado
. Este resultado é bastante contraintuitivo. Por outro lado, acrescentar
um fóton a um estado coerente, altera o estado do feixe de laser. Contudo, pela
correspondência dual temos
(108)
Além das propriedades já mencionadas, os estados coerentes são também conhecidos
por apresentarem incerteza mínima. Para que essa propriedade seja demonstrada, é
conveniente neste momento definirmos os operadores de quadratura
e
em função dos
operadores de aniquilação e criação de fótons:
(109)
Enquanto o operador
está relacionado ao campo elétrico (Eq, 77), o operador
está
associado ao campo magnético. Para um fim de comparação, podemos calcular a variância do
operador
nos estado de Fock
como
(110)
e a variância de
em um estado coerente
como
32
(111)
Já que a variância de
representa a média da flutuação do campo elétrico no estado,
vemos que a flutuação do campo elétrico em um estado de Fock é sempre maior ou igual a
variância em um estado coerente. O mesmo é válido para as flutuações do campo magnético.
Finalmente, sabemos que o princípio da incerteza de Heisenberg impõe uma restrição
na precisão com que se podem efetuar medições simultâneas de uma classe de pares de
observáveis, o que aplicado às medições de posição e momento linear, define a seguinte lei:
(112)
Partindo-se do cálculo da variância de
e
em um estado coerente, descobrimos que
(113)
o que prova que um estado coerente realmente é um estado de incerteza mínima.
Outro resultado curioso é obtido no cálculo da probabilidade de se obter
fótons em
uma medição em um estado coerente. Essa probabilidade pode ser definida como:
(114)
e tem como resultado
(115)
É interessante notar que a chance de se obter um certo número
de um estado coerente
de fótons na medição
obedece a uma distribuição de Poisson.
3 METODOLOGIA
Como se trata de um projeto de caráter teórico, para sua realização não foram
utilizados materiais nem equipamentos necessários para experimentos. A metodologia
33
empregada consistiu em realizar, inicialmente, uma revisão bibliográfica dos postulados da
física quântica e de suas interpretações. Em seguida, realizamos um estudo dos sistemas de
dois níveis, do oscilador harmônico quântico e do modelo de Jaynes-Cummings, tendo
deduzido todos os resultados apresentados nas seções 2.2, 2.3, 2.4 e 2.5, independentemente
deles já existirem na literatura.
Após a revisão bibliográfica, diagonalizamos o hamiltoniano de Jaynes-Cummings e
obtivemos as energias permitidas (autovalores) e os autoestados do sistema. Aplicamos a
equação de Schrödinger, obtivemos a evolução temporal do estado que descreve o sistema e,
com ela, calculamos a probabilidade de transição do átomo, que pôde ser comparada com
resultados experimentais. Calculamos a inversão de população e o número de fótons do
sistema dentro de uma cavidade e analisamos os resultados obtidos. Finalmente determinamos
a evolução temporal do sistema formado por um átomo em interação com um estado coerente
de luz e observamos os fenômenos de colapsos e revivais, comparando-os também com
resultados experimentais. As etapas mencionadas estão descritas com mais detalhes a seguir.
A) Revisão bibliográfica sobre a física quântica
Neste período, realizamos uma revisão bibliográfica da física quântica com ênfase no
entendimento dos postulados, em suas interpretações e no formalismo quântico necessário
para o desenvolvimento do projeto. Introduzimos o quadro da interação e neste quadro,
obtivemos a evolução temporal dos operadores
e
usando a equação de
Heisenberg.
B) Propriedades de um sistema atômico de dois níveis
Nesta etapa, deduzimos as propriedades de um sistema de dois níveis usando técnicas
de física quântica. Os autovalores e os autovetores de um átomo de dois níveis foram
calculados e pudemos entender a ação dos operadores
e
.
C) Propriedades do oscilador harmônico
Nesta etapa, deduzimos as propriedades do oscilador harmônico unidimensional, em
especial o espectro de energia do sistema e seus autoestados, e nos familiarizamos com o
formalismo dos operadores de aniquilação e de criação.
34
D) Modelo de Jaynes-Cummings
Nesta etapa, entendemos como a interação entre o campo elétrico e um dipolo elétrico
leva ao hamiltoniano de interação proposto por Jaynes e Cummings. Simplificamos o
hamiltoniano de Jaynes-Cummings ao desprezar os termos que não preservam o número de
excitações do sistema e introduzimos uma representação matricial para o operador
hamiltoniano no caso geral de
fótons e no caso particular de
fóton.
E) Interação de um sistema de dois níveis com um único fóton
Usando as técnicas desenvolvidas anteriormente, diagonalizamos o hamiltoniano e
obtivemos as energias e os autoestados de um sistema de dois níveis interagindo com
fótons. Estudamos com mais profundidade o caso particular
fóton e obtivemos a
evolução temporal de um estado quântico que descreve o sistema físico estudado. Ainda neste
caso, conseguimos calcular a probabilidade de transição do sistema tendo a chance de
observar as oscilações de Rabi no resultado teórico deduzido. O resultado foi comparado com
os dados experimentais disponíveis na literatura.
F) Estados coerentes de luz
Nesta etapa, deduzimos as propriedades dos estados coerentes, fizemos sua
representação em termos dos estados de Fock
obtivemos a distribuição de probabilidade
estado coerente
com número de fótons definidos e
de encontrar
fótons em um
.
G) Revivais quânticos
Nesta etapa, obtivemos, no quadro da interação, a evolução temporal de um estado
físico inicialmente descrito por
usando a equação de Schrödinger. Calculamos
a probabilidade de encontrar o sistema no estado inicial e comparamos os resultados obtidos
com os colapsos e revivais observados por Rempe, Walther e Klein em sistemas compostos
por átomos de rubídio em interação com estados coerentes da radiação no interior de uma
cavidade[22].
35
4 RESULTADOS
Nesta seção, descreveremos os resultados obtidos no contexto do modelo de JaynesCummings. Inicialmente, vamos obter os autoestados do sistema, nos quais o átomo está
vestido pelo campo de luz. Por analogia com os estados de partículas vestidas da
eletrodinâmica quântica[17], estes estados podem ser chamados estados vestidos. Indicaremos
as características de emaranhamento quântico do sistema introduzidas pela interação entre
átomo e fótons no interior da cavidade.
Em seguida, usaremos os estados vestidos para obter a probabilidade de transição
de encontrar o sistema no estado
após ter sido preparado no estado
. Este resultado
será comparado ao obtido experimentalmente por Brune e colaboradores[18]. Adicionalmente,
calcularemos a inversão da população atômica e o número de fótons na cavidade como função
do tempo e obteremos a matriz densidade que descreve as propriedades estatísticas e de
coerência do sistema.
Para finalizar o trabalho, utilizaremos a equação de Schrödinger no quadro de Dirac
para calcular a evolução temporal de um sistema composto por um átomo de dois níveis em
interação com um estado coerente de luz. Calcularemos a probabilidade de encontrar o
sistema em seu estado inicial após um intervalo de tempo . Compararemos os resultados com
os colapsos e revivais observados por Rempe e colaboradores[22] em sistemas compostos por
átomos de rubídio em interação com estados coerentes de radiação.
4.1 Estados vestidos e emaranhamento quântico
A interação entre átomo e campo dentro da cavidade fortemente acoplada faz com que
ocorra um desdobramento dos estados atômicos, dando origem a novos estados. Estes estados
são denominados estados vestidos, e representam um sistema no qual o átomo se encontra
vestido pelos fótons do campo de luz.
Os estados desacoplados formam a base nas quais as medições das propriedades do
sistema são usualmente efetuadas enquanto os estados vestidos formam a base na qual a física
realmente acontece, onde a dinâmica da interação entre átomo e luz é observada.
36
Os estados vestidos são autoestados do hamiltoniano de Jaynes-Cummings, estados
em que suas energias são bem definidas, e suas energias são os autovalores, obtidos através da
diagonalização, da matriz Ĥ .
Para o caso com n fótons na cavidade, em que o modelo de Jaynes-Cummings é
representado pela equação (96), os autovalores, ou seja, as energias obtidas através da
diagonalização desta matriz são:
(116)
associadas respectivamente, aos estados vestidos
e
.
Este resultado permite entender como a energia do sistema depende da dessintonia,
como mostrado na figura 4. Podemos observar que quanto maior for o módulo da dessintonia,
maior é a diferença de energia entre os estados vestidos e portanto, menos acoplados estão
átomo e fóton. Para
, a interação entre os estados desacoplados
máxima e a diferença de energia entre os estados vestidos é mínima,
e
é
. Quando a
dessintonia é grande, átomo e luz interagem cada vez menos e as energias tendem aos valores
de energia dos estados desacoplados, representados pelos extremos laterais do gráfico abaixo.
Figura 4: Energias dos estados vestidos em função da dessintonia.
Para o caso particular importante em que temos 0 ou 1 fótons na cavidade, as energias
dos estados vestidos são simplificadas para
37
(117)
que nos permite escrever os estados vestidos como:
(118)
A partir da equação (118), é fácil constatar que os estados vestidos são uma
superposição não-separável de estados puros, isso porque há uma correlação quântica entre o
átomo e o campo. A esta correlação é dado o nome de emaranhamento.
O emaranhamento é um fenômeno da mecânica quântica referente à inseparabilidade
das partes de um sistema isolado e nos permite descobrir informações sobre algumas partes do
sistema realizando medições apenas sobre outras partes do sistema, de forma que uma parte
não pode ser descrita sem que sua contraparte emaranhada seja mencionada. Esta
característica da interação átomo-fóton pode ser explorada em um esquema de medição
quântica não destrutiva[15] ou medição QND (Quantum Nondemolition). Tradicionalmente,
para descobrir o número de fótons na cavidade, seria preciso contá-los com um detector de luz
que absorveria todos os fótons, destruindo o sistema do qual obtivemos informação. Em uma
medição QND, o emaranhamento entre o estado atômico e o estado do campo de luz permite
que obtenhamos informação sobre o campo de luz sem jamais perturbá-lo, simplesmente ao
medir o estado atômico emaranhado[16]. Vale lembrar que os estados vestidos são
naturalmente emaranhados e representam a situação em que o emaranhamento é máximo.
Os estados desacoplados também podem ser escritos em função dos estados vestidos,
em uma relação de mudança de base que será posteriormente utilizada
(119)
4.2 Probabilidade de transição e as oscilações de Rabi
Calcular a evolução temporal do sistema interagindo dentro da cavidade, nos permite
descobrir como ele se comporta em função do tempo. Considerando o sistema dentro da
cavidade
como uma superposição de estados vestidos, temos:
38
(120)
onde
e
assumem valores entre 0 e 1 e representam, respectivamente, as
probabilidades de encontrarmos, dentro da cavidade, o sistema no estado
ou no estado
.
De forma análoga à revisão bibliográfica, a evolução temporal do estado pode ser
calculada através da equação de Schrödinger
(121)
Ĥ
da qual obtemos
(122)
e os coeficientes
e
dependem do estado do sistema em
e obedecem a relação
(123)
que garante a conservação da probabilidade durante a evolução temporal.
Uma evidência da característica quântica da luz é encontrada quando calculamos a
probabilidade de transição
preparado no estado
de encontrar o sistema no estado
Neste caso, descobrimos que
após ter sido
e que, portanto,
(124)
A probabilidade de transição
sido preparado no estado
de encontrar o sistema no estado
após ter
é dada por
(125)
Na situação de ressonância em que
e, portanto,
, a diferença de energia
entre os estados vestidos pode ser escrita como
(126)
e a probabilidade de transição
é
39
(127)
Este resultado pode ser comparado com o obtido em um experimento em
eletrodinâmica quântica em cavidades por Brune e colaboradores[18]. No experimento, átomos
de rubídio foram preparados no estado excitado
quântico principal
, um estado de Rydberg com número
, e enviados um por um em direção a uma cavidade na qual havia
apenas o campo eletromagnético de vácuo. Após a interação com o vácuo da cavidade, o
estado de cada átomo foi medido por ionização seletiva ao estado
Rydberg com número quântico principal
, outro estado de
, e a probabilidade de transição
foi
medida. A figura 5 mostra o resultado teórico que deduzimos juntamente com o resultado
experimental obtido por Brune e colaboradores[18]. Podemos verificar que a probabilidade de
encontrar o átomo no estado fundamental oscila com o tempo em uma frequência compatível
com a determinada experimentalmente. Estas oscilações são chamadas oscilações de Rabi
associadas à frequência de Rabi
por semelhança com o fenômeno análogo que ocorre em
ressonância magnética nuclear[19].
Figura 5: Oscilações de Rabi para o caso
e
constante de acoplamento do experimento de Brune et al.
.. A curva teórica foi calculada usando a
[18]
do qual foram extraídos os dados experimentais.
Podemos observar que, experimentalmente, as oscilações têm sua amplitude reduzida
à medida que o tempo passa enquanto a previsão teórica é de oscilações com amplitude
constante. A discrepância é causada pelo fato de que, no experimento, os átomos não estão em
40
repouso no interior da cavidade mas passam por ela com uma velocidade média de
em
. Estes átomos permanecem na região central, onde a interação é semelhante à
estudada no nosso modelo teórico, em torno de
pois a largura do modo eletromagnético
da cavidade é de apenas
Excetuando os casos extremos em que a probabilidade valeria exatamente 0 ou 1 e o
sistema seria descrito por um dos dois estados desacoplados, o que acontece é que há um certo
nível de emaranhamento correspondendo a uma superposição de estados vestidos.
Particularmente quando
, o emaranhamento é máximo e o
sistema possui todas as características descritas na seção 4.1.
Portanto, é possível concluir que controlando-se o tempo que o átomo permanece na
cavidade, ou seja, o tempo de interação entre átomo e campo eletromagnético, podemos
definir o grau de emaranhamento apresentado pelo sistema.
4.3 Inversão da população e número de fótons
A inversão da população e o número de fótons na cavidade como função do tempo
foram dois outros resultados obtidos nesta etapa do projeto. Para ambos os casos, considerouse o sistema em ressonância e a existência de uma única excitação na cavidade. Deste modo,
haveria no máximo um fóton na cavidade, em qualquer instante de tempo.
A inversão da população pode ser entendida como o número de átomos no estado
excitado menos o número de átomos no estado fundamental e é representada pelo operador
. O valor médio desta grandeza no sistema no estado descrito por
equação (29), dado por
é, conforme a
.
Como resultado, temos que
(128)
representando, justamente, como a população de átomos excitados se comporta dentro da
cavidade com o passar do tempo. Como na cavidade só há um único átomo, este resultado é
equivalente à probabilidade deste átomo ser encontrado no estado excitado.
41
Já a média do número de fótons é definida como
, e, neste caso, é
equivalente à probabilidade de encontrarmos exatamente um fóton dentro da cavidade.
(129)
A figura 6 mostra as previsões para a inversão da população e para o número médio de
fótons na cavidade em função do tempo. Podemos entender o resultado mostrado da seguinte
maneira. Quando
, ou seja, o átomo na cavidade está no estado excitado, temos
, representando que, como já era esperado, não há fótons dentro da cavidade, pois o
mesmo foi utilizado para excitar o átomo. Para o caso oposto, em que o átomo na cavidade
está no estado de menor energia (
na cavidade (
), temos 100% de chance de encontrarmos 1 fóton
). Sendo assim, tanto a população atômica oscila entre os estados
e o número de fótons na cavidade oscila entre os estados
Figura 6: Inversão da população
e número médio de fótons
caso
e
e
com frequência
e
.
na cavidade em função do tempo para o
.
42
4.4 O operador densidade
O operador densidade descreve aspectos estatísticos relacionados a um sistema
quântico misto. A descrição estatística do sistema através do operador densidade é necessária
quando o sistema em questão é formado por n sistemas diferentes ou quando não se conhece a
forma como o sistema foi preparado e, consequentemente, não se tem certeza absoluta sobre
qual estado quântico puro o sistema se encontra[20].
Como o operador densidade é definido como
(130)
e como
, representado na base dos estados vestidos, é dado por
(131)
a representação matricial do operador densidade, conhecida como matriz densidade será
(132)
Nesta representação, os elementos diagonais nos dão informação sobre a população do
respectivo estado e os elementos fora da diagonal principal são chamados de coerências e dão
informação sobre a fase relativa entre os estados e a capacidade de haver interferência entre
eles. Na base dos estados vestidos, tanto a população de estados
como a de estados
são constantes e apresentam probabilidade de 50% de encontrarmos o sistema em cada um
deles.
Podemos observar também, que uma das propriedades da matriz densidade é que a
soma dos elementos que compõem a diagonal principal (traço) será sempre igual a 1,
correspondendo à normalização da probabilidade.
Considerando-se agora
sendo representado na base desacoplada,
(133)
43
a matriz densidade será
(134)
Assim, na base desacoplada, a população do estado
e a população do estado
oscila segundo
oscila entre 0 e 1 segundo
, e a coerência entre estes
estados é representada por
(135)
indicando a possibilidade de interferência entre os estados.
4.5 Colapsos e revivais quânticos
O estudo da interação entre a luz e a matéria baseado no modelo de Jaynes-Cummings,
nos permitiu, até o presente momento, descrever alguns dos fenômenos apresentados por este
sistema. Porém, como já foi discutido anteriormente, modelar um feixe de laser como um
estado de Fock não é o procedimento mais adequado uma vez que estados de Fock, com
número bem definido de fótons, apresentam características quânticas que estão em desacordo
com o esperado da luz clássica de um laser.
Com isso, nesse estágio do projeto, finalizamos nossos estudos baseados em sistemas
formados por um átomo de dois níveis em interação com um campo eletromagnético que
possui um número definido de fótons e passamos agora, a tratar a luz clássica de um laser por
um modelo mais realista, os estados coerentes.
Neste caso, o sistema que antes era descrito pela equação (133), passa agora a ser
representado por
(136)
44
evidenciando mais uma vez, que um estado coerente é uma superposição de estados com
todos os números de fótons possíveis, ou seja, uma superposição de estados de Fock.
Os coeficientes
coeficiente
e
em princípio, apresentam dependência temporal. Já o
é definido como
(137)
de forma que represente um átomo em interação com um estado coerente de radiação.
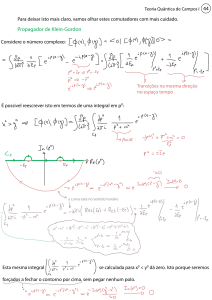
O problema da evolução temporal do sistema representado por
na equação
(136) já foi resolvido por Eberly e colaboradores[21] utilizando a abordagem do quadro de
Heisenberg. A solução é bastante complexa pois se baseia na evolução temporal de um
conjunto de operadores quânticos sem significado físico imediato, sendo, portanto, pouco
natural ainda que formalmente correta. O método que utilizaremos para se analisar a evolução
temporal de um átomo em interação com um feixe de laser é mais simples que o proposto na
referência [21] e se baseia no quadro de Dirac. Até onde sabemos, é um tratamento inédito e
mostrou-se conveniente pela relativa simplicidade quando comparado à solução do problema
no quadro de Heisenberg.
O sistema representado por
será inicialmente descrito por
(138)
e utilizaremos a equação de Schrödinger para o quadro da interação, pois como vimos
anteriormente, é a equação que rege a evolução temporal dos estados dos observáveis
(139)
onde
(140)
porém, como consideraremos o caso de ressonância em que
, o
hamiltoniano de interação se resume a
(141)
45
A resolução da equação de Schrödinger para a interação nos fornece outras duas
equações:
(142)
As equações diferenciais obtidas desacoplam facilmente levando a uma equação de segunda
ordem equivalente à do oscilador harmônico. A solução geral para este caso é
(143)
Como o estado inicial do sistema
é formado por um átomo excitado em
interação com um estado coerente de luz, obtemos
e
, o que nos leva a
(144)
e a amplitude de probabilidade do estado fundamental
(145)
Reescrevendo a equação (136) obteremos
(146)
que é a solução final da evolução temporal de um sistema formado pela interação entre um
átomo de dois níveis e um estado coerente de luz.
Considerando-se agora o caso mais geral, com dessintonia diferente de zero (
),
teríamos para a amplitude de probabilidade do estado excitado e fundamental respectivamente
(147)
ambas levando a
46
(148)
com
(149)
Porém, mais interessante que descobrir como o estado evolui no tempo, é descobrir
como a inversão de população se comporta de acordo com a evolução do sistema. Para isso,
calcularemos o valor médio do operador
conforme a equação (29), é dado por
no estado descrito por
e
que,
.
Como resultado, temos que
(150)
que pode ser simplificado para
(151)
Deve-se notar que o resultado é uma série infinita da qual não se conhece solução
analítica em forma fechada. Para estudar seu comportamento, foi necessário realizar a soma
numericamente. Para os parâmetros que serão utilizados a seguir, verificamos que os
primeiros 150 termos eram mais do que suficientes para que o erro da soma fosse inferior a
1%.
47
Figura 7: Inversão da população
na cavidade composta por um estado coerente em função do tempo, para o
caso em que
e
fótons.
A figura 7 nos permite constatar a existência de um fenômeno conhecido como
colapsos e revivais. Os colapsos e os revivais surgem a partir da interação de um átomo com
um estado coerente de luz, por causa da defasagem, provocada pela diferença de frequência,
entre cada um dos estados de
fótons que formam o estado coerente.
Podemos entender o resultado observado da seguinte maneira: assim que o sistema é
colocado para interagir, temos uma maior probabilidade de encontrarmos o átomo ou no
estado excitado ou no estado de menor energia, de maneira discreta. Por conta da
incomensurabilidade das frequências de oscilação de cada termo da série, a coerência quântica
colapsa, reduzindo a zero o valor da inversão de população. Porém, de tempos em tempos, os
diversos termos da série voltam a se encontrar quase em fase novamente, e a coerência
quântica ressurge parcial mas espontaneamante em um fenômeno chamado de revival.
Se compararmos a inversão de população quando a radiação dentro da cavidade era
descrita por um estado de Fock (figura 6) com os resultados obtidos agora, onde a luz é
representada por um estado coerente, veremos de imediato que além de não termos uma
variação constante durante o regime de estado estacionário, nos sistemas em que a luz é
descrita por um estado coerente, o valor da inversão de população não é bem definido devido
à influência do princípio da incerteza de Heisenberg.
No caso de dessintonia não nula,
, obtemos, para a inversão de população,
48
(152)
e percebemos que não há grandes diferenças entre o caso de ressonância e o de dessintonia
diferente de zero, pelo menos quando utilizados valores razoáveis para as dessintonias. Talvez
por este motivo, este caso parece ausente da literatura até o momento.
Ainda que a análise da inversão da população já evidencie a existência de colapsos e
revivais no sistema estudado, parece ser mais simples medir a probabilidade
de
encontrar o átomo no estado excitado. Esta grandeza, relacionada à inversão da população, é a
que foi determinada em experimentos pioneiros realizados ainda na década de 1980[22]. Para
poder comparar nossos resultados com as medições realizadas, calculamos a probabilidade
de encontrar o átomo no estado excitado, que é o estado inicial do sistema.
Considerando-se o sistema em situação de ressonância (
), temos
(153)
com
(154)
e podemos perceber como a inversão de população está intimamente relacionada à
probabilidade do átomo estar excitado.
Os resultados obtidos pela soma numérica dos primeiros 150 termos da série
representada na equação (153) foram comparados aos resultados experimentais obtidos por
Rempe, Walther e Klein[22] na figura 8. Os resultados são qualitativamente semelhantes e
parecem concordar de modo bastante razoável do ponto de vista quantitativo. O experimento
foi feito utilizando um sistema formado pela interação entre átomos de rubídio e estados
coerentes de luz. Percebemos que entre
constante. Após isso,
e
a probabilidade
é praticamente
volta a oscilar novamente, iniciando o fenômeno de revival.
49
Figura 8: Probabilidade de se encontrar o sistema no estado inicial na interação entre átomos e estados coerentes
de luz, para o caso em que
e
.
5 CONCLUSÃO
Durante o projeto, a revisão bibliográfica permitiu o entendimento dos postulados e
interpretação do formalismo quântico envolvido em seu desenvolvimento. O estudo realizado
permitiu que modelos quânticos fossem usados tanto para descrever o átomo como um
sistema de dois níveis quanto para descrever o campo eletromagnético como um conjunto de
osciladores harmônicos. A interação entre estes sistemas foi descrita pelo modelo de JaynesCummings.
No contexto do modelo de Jaynes-Cummings, diagonalizamos o Hamiltoniano,
obtivemos a probabilidade de transição e comparamos nossos resultados com resultados
obtidos experimentalmente[18]. A comparação sugere que o modelo de Jaynes-Cummings é
capaz de descrever a interação de um átomo com o campo eletromagnético de modo bastante
acurado no que diz respeito às trocas de energia entre o átomo e a luz.
50
Porém, a luz clássica de um laser é dotada de uma complexidade um pouco maior do
que aquela que pode ser representada por estados de Fock puros. Com isso, o entendimento da
radiação a partir de sua descrição por estados coerentes permitiu que estas características
peculiares fossem descritas tanto para a luz como um sistema isolado, quanto para sua
interação com a matéria. A introdução do princípio da incerteza de Heisenberg durante o
desenvolvimento das propriedades dos estados coerentes deixou ainda mais clara a
interpretação probabilística que a física quântica nos permite fazer da natureza. A partir disso,
pudemos utilizar o quadro de Dirac para a realização dos cálculos envolvendo os estados
coerentes de luz e sua interação com modelos atômicos de dois níveis, método que não foi
encontrado na literatura e que, no entanto, mostrou-se mais simples que os utilizados por
outros autores.
Calculamos a evolução temporal desse sistema e comparamos nossas previsões
teóricas com os resultados obtidos experimentalmente[22]. Esta comparação permitiu que
concluíssemos que os modelos utilizados neste trabalho são adequados para descrever de
modo acurado os fenômenos de interação entre radiação e matéria.
6 REFERÊNCIAS BIBLIOGRÁFICAS
[1] LEOŃSKY, W.; TANAŚ, R. Possibility of producing the one-photon state in a kicked
cavity with a nonlinear Kerr medium. Physical Review A v.49, p.R20, 1994.
[2] BERTET, P. et al. Generating and probing a two-photon Fock state with a single atom in a
cavity. Physical Review Letters v.88, p.143601, 2002.
[3] GLAUBER, R.J. Coherent and incoherent states of the radiation field. Physical Review
v.131, p.2766, 1963.
[4] VAN ENK, S.J.; FUCHS, C.A. Quantum state of an ideal propagating laser field.
Physical Review Letters v.88, p.027902, 2001.
[5] DIRAC, P.A.M. The Principles of Quantum Mechanics. 4.ed. Oxford: Oxford
University Press, 1958.
51
[6] ARFKEN, G. Mathematical Methods for Physicists. 3.ed. San Diego, CA: Academic,
1985.
[7] SAKURAI, J.J. Modern Quantum Mechanics. Reading, MA: Addison-Wesely, 1985.
[8] SCULLY, M.O.; ZUBAIRY, M.S. Quantum Optics. Cambridge: Cambridge University
Press, 1997.
[9] JONES, R.V. Optical Physics and Quantum Electronics: Lecture Notes. Cambridge,
MA:
Harvard
University,
2000.
Disponível
em:
<http://people.seas.harvard.edu/~jones/ap216/lectures/lectures.html>. Acesso em: 18 dez.
2009.
[10] KRYSZEWSKI, S. Quantum Optics : Lecture Notes. Gdańsk: Uniwersitetu
Gdanskiego, s.d. Disponível em: <http://iftia9.univ.gda.pl/~sjk/skok/indexOK.html>. Acesso
em: 18 dez. 2009.
[11] WALLS, D.F.; MILBURN, G.J. Quantum Optics. Berlin: Springer, 1995.
[12] LEOŃSKY, W.; TANAŚ, R. Possibility of producing the one-photon state in a kicked
cavity with a nonlinear Kerr medium. Physical Review A v.49, p.R20, 1994.
[13] BERTET, P. et al. Generating and probing a two-photon Fock state with a single atom in
a cavity. Physical Review Letters v.88, p.143601, 2002.
[14] JAYNES, E.T.; CUMMINGS, F.W. Comparison of quantum and semiclassical radiation
theories with application to the beam maser. Proceedings of the IEEE v.51, p.89, 1963.
[15] BRAGINSKY, V.B.; KHALILI, F. Ya. Quantum nondemolition measurements: the route
from toys to tools. Reviews of Modern Physics v.68, p.1, 1996.
[16] GLEYZES, S. et al. Quantum jumps of light recording the birth and death of a photon in
a cavity. Nature v.446, p.297, 2007.
[17] MOREIRA, M.A. O modelo padrão da física de partículas. Revista Brasileira de
Ensino de Física v.31, p.1306, 2009.
[18] BRUNE, M.; SCHMIDT-KALER, F.; MAALI, A.; DREYER, J.; HAGLEY, E.
RAIMOND, J.M.; HAROCHE, S. Quantum Rabi oscillation: a direct test of field quantization
in a cavity. Physical Review Letters v.76, p.1800, 1996.
52
[19] RABI, I.I. Space quantization in a gyrating magnetic field. Physical Review v.51, p.652,
1937.
[20] FANO, U. Description of states in quantum mechanics by density matrix and operators
techniques. Reviews of Modern Physics v.29, p.74, 1957.
[21] NAROZHNY, N. B.; SANCHEZ-MONDRAGON, J. J.; EBERLY, J. H. Coherence
versus incoherence: collapse and revival in a simple quantum model. Physical Review A
v.23, p.236, 1981.
[22] REMPE, G.; WALTHER, H.; KLEIN, N. Observation of quantum collapse and revival
in a one-atom maser. Physical Review Letters v.58, p.353, 1987.
53