Segunda Lista de Exercícios Eletricidade Básica

1
Eletotécnica Aplicada (ETE)- Segunda Lista de Exercícios
Segunda Lista de Exercícios
Eletricidade Básica
(Material original do Prof.: Leonardo Nepomuceno)
OBSERVAÇÃO: Esta lista de exercícios avalia o conteúdo ministrado em sala de aula e o conteúdo
descrito nos capítulos 11, 12, 13 e 14 do livro texto: ELETRICIDADE BÁSICA, Milton Gussow.
1) A tensão de pico de uma onda seno CA é de 100 V. Calcule a tensão instantânea em 0 o ,
30 o , 60 o , 90 o , 135o , 245o . Qual o seu valor eficaz? Qual a representação fasorial desta onda,
se ela está adiantada de 30 graus em relação a uma onda de referência? Resp: 0, 50V, 86.6V,
100V, 70.7V,-90.6V, 70.71, 70.7130 o .
2) Para a onda descrita no exercício anterior, qual deve ser o valor medido se utilizarmos um
aparelho de medição desta onda (voltímetro). Resp.: 70.71V.
3) Um forno elétrico consome 7.5 A de uma fonte de alimentação CC de 120 V. Qual o valor
máximo de uma corrente alternada capaz de produzir o mesmo efeito térmico? Calcule a
potência consumida em CA. Resp.: 10.6A, 900W.
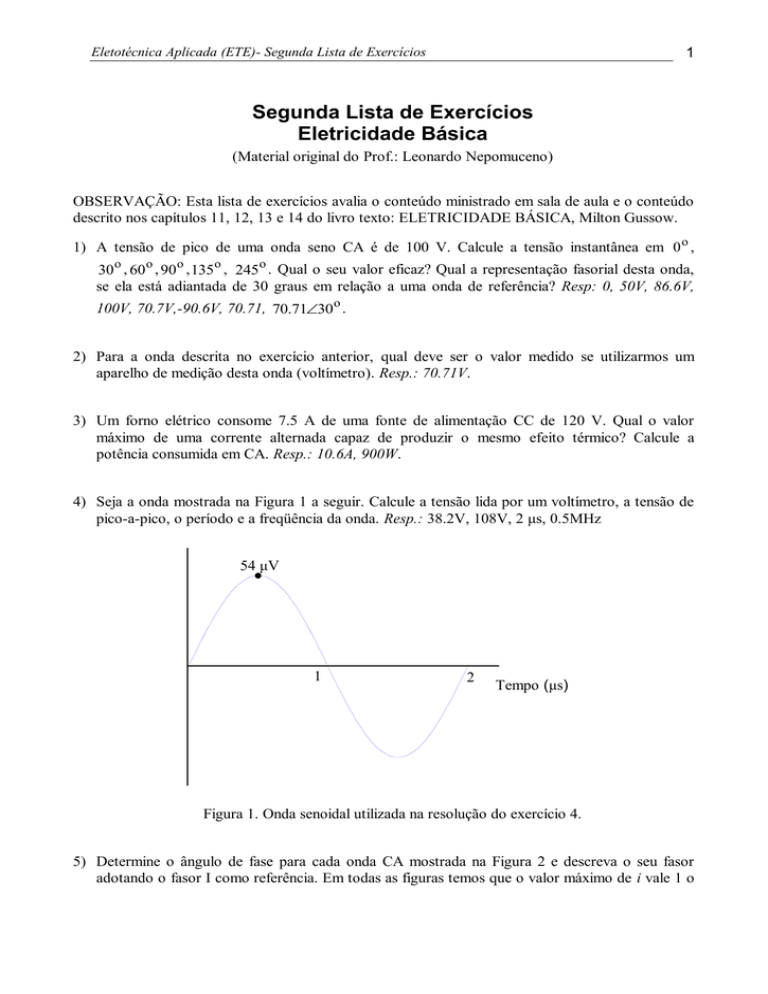
4) Seja a onda mostrada na Figura 1 a seguir. Calcule a tensão lida por um voltímetro, a tensão de
pico-a-pico, o período e a freqüência da onda. Resp.: 38.2V, 108V, 2 μs, 0.5MHz
54 μV
1
2
Tempo (μs)
Figura 1. Onda senoidal utilizada na resolução do exercício 4.
5) Determine o ângulo de fase para cada onda CA mostrada na Figura 2 e descreva o seu fasor
adotando o fasor I como referência. Em todas as figuras temos que o valor máximo de i vale 1 o
2
Eletotécnica Aplicada (ETE)- Segunda Lista de Exercícios
valor máximo de v vale 3. Resp.: a) V  2.120 o , I  0.700 o b) V  2.12180o , I  0.700o
c) V  2.12  90o , I  0.700o d) V  2.12  90o , I  0.700o .
v
v
i
360o
360o
180
o
o
180
i
v
v
i
i
90o
180o
90o
180o
Figura 2. Ondas senoidais utilizadas na resolução do exercício 5.
6) Calcule a corrente e a potência consumidos de uma linha de alimentação de 110 V e 60 Hz por
uma lâmpada de filamento de tungstênio cuja resistência é de 275 Ω. Faça o diagrama de fasores.
Resp.: I=0.4A ; P=44W. A corrente e a tensão estão em fase.
7) Para o circuito mostrado na Figura 3 calcule a corrente total I T , a corrente que passa em cada
resistência e a tensão através de cada resistência. Faça o diagrama fasorial de todas as grandezas
envolvidas utilizando a tensão total como referência. Resp.: I T  24 A , I 2  12 A  I 3 ,
V1  96V , V2  V3  24V .
R1  4
V  120V ~
f  60 Hz
IT
I3
I2
R2  2
R3  2
Figura 3. Circuito utilizado na resolução do exercício 7.
3
Eletotécnica Aplicada (ETE)- Segunda Lista de Exercícios
8) Uma corrente constante de 20 mA percorre uma bobina com uma indutância de 100 mH. Qual a
tensão induzida na bobina? Resp. 0 V.
9) Uma corrente que passa por uma bobina aumenta até o valor de 20 A em um tempo de 1/1000 s.
Se a indutância da bobina for de 100 μH, qual será a tensão induzida neste instante? Resp.: 2V.
10) Uma corrente CA, de 120Hz e 20 MA, está presente em um indutor de 10H. Qual a reatância do
indutor e a queda de tensão através do indutor. Quais os valores eficaz e máximo da tensão
desenvolvida no indutor? Resp.: 7.536 Ω, 150.7 V, 150.7V, 213,1V.
11) Uma bobina de choque de 225 μH de resistência desprezível serve para limitar a corrente a 25
mA quando aos seus terminais são aplicados 40 V. Qual a freqüência da corrente. Resp. 1 MHz.
12) Qual a indutância total vista dos terminais a b do circuito da Figura 4. Qual a reatância
enxergada entre os pontos a e b se for aplicada uma freqüência de 2 MHz . Resp.: 12mH,
150.720Ω.
L1  10mH
a
L3  6mH
L2  3mH
b
Figura 4. Circuito para o exercício 12.
13) Calcule a indutância equivalente vista dos pontos a e b para os circuitos da Figura 5. Resp.: 28H,
16H.
LM  3H
LM  3H
L1  9H
a
L1  9H
L2  13H
b
a
L2  13H
b
Figura 5. Circuitos para o exercício 13.
14) Uma bobina de 20H é ligada a uma linha de alimentação CA de 110 V e 60 Hz. Se a bobina tiver
uma resistência interna nula , qual a corrente e as potência ativa, reativa e aparente consumidas ?
4
Eletotécnica Aplicada (ETE)- Segunda Lista de Exercícios
Desenhe o diagrama fasorial mostrando todos os fasores envolvidos. Resp.: 14.6 mA, 0W, 1.60
VAR, 1.60VA.
15) Uma bobina de sintonia tem uma indutância de 39.8 μH e uma resistência interna de 20 Ω.
Calcule a sua impedância para uma freqüência de 100KHz e a corrente através da bobina se a
queda de tensão for de 80 V através de toda a bobina. Calcule também a queda resistiva e a
queda indutiva da bobina e desenhe o diagrama fasorial, adotando a corrente como referência.
Resp.: 32.0551.3o  , 2.50 o A , VR  500 o V , VL  62.590o V .
16) A finalidade de um filtro passa - alta (Figura 6) é a de permitir que altas freqüências passem para
a carga e evitar a passagem das baixas freqüências. Calcule as correntes nos ramos I L e I R , a
corrente total I T , e a porcentagem da corrente total que passa pelo resistor da figura 6, quando
for aplicado ao circuito (a) um sinal de audiofreqüência (baixa) de 80 V e 1.5KHz (b) um sinal de
radiofreqüência (alta) de 80 V, 1 MHz. Resp.: (a) I L  0.425; I R  0.016 , 3.8% (b)
I L  0.637mA; I R  16mA , 99.9%
IT
a
IL
L  20mH
IR
R  5000
b
Figura 6. Circuito para o exercício 16.
17) Uma resistência de 500 Ω está em paralelo com uma reatância X L  300 sendo o conjunto
alimentado por uma tensão CA de 500V. Calcule I T ,  , e Z T . Se a freqüência for duplicada
então recalcule estas variáveis. Resp.: 1.95A, -59.1o, 256.4, 1.56 A, -39.8o , 384.6.
18) Um motor de indução funcionando com um fator de potência de 0.8 consome 1056 W de uma
linha de alimentação CA de 110 V. Qual a corrente ? Resp.: I= 12 A.
19) Um resistor de 20 Ω e uma reatância indutiva de 15 Ω estão dispostos em paralelo em uma linha
CA de 120 V. Calcule as correntes nos ramos, a corrente total, a impedância e a potência
consumida;
desenhe
o
diagrama
fasorial.
Resp.
I L  8 A; I R  6 A; IT  10 A; ZT  12; P  720W
20) Para o circuito da Figura 7 calcule (a) a reatância indutiva (b) a impedância total (c) o valor rms
(eficaz)
da
corrente
e
(d)
a
corrente
de
pico.
Resp.:
(a) X L  37.7 (b) Z  41 ( R  16) (c) I  5.85 A (d ) I p  8.27 A
5
Eletotécnica Aplicada (ETE)- Segunda Lista de Exercícios
0.5
V  240V
60 Hz
RL  15
~
L  100mH
0.5
Figura 7. Circuito para o exercício 20.
21) Qual a capacitância total de 3 capacitores de 0.20μF, 0.20μF e 0.10μF ligados em paralelo. Se
estes capacitores forem ligados em série, qual será a capacitância total. Resp,: 0.50 μF; 0.05 μF.
22) Calcule a capacitância total e a reatância capacitiva total de três capacitores de 0.10μF, 0.50μF e
0.25μF ligados em série a um circuito de 60 Hz. Resp.: 0.0625 μF, 42.4 Ω.
23) Um capacitor é introduzido em um circuito para se obter uma corrente adiantada de 5 A. Se a
tensão for de 110V em 60 Hz, qual a capacitância.Resp.: 121 μF.
24) Calcule a impedância de uma associação RC quando o capacitor de acoplamento é de 0.01 μF a
freqüência de áudio de 1 KHz e a resistência é de 3 KΩ. Resp.: 16.18079.3o .
25) Uma capacitância de 3.53 μF e uma resistência de 40 Ω estão ligadas em série através de uma
fonte CA de 110V e 1.5 KHz. Calcule X c , Z ,  , I , V R , Vc , P . Resp.: X c  30 ,
Z  50 ,   36.9 o , I  2.2 A , VR  88V , Vc  66V , P  193.6W . Desenhe o diagrama
fasorial do circuito.
26) Para o circuito RLC série da Figura 8 calcule as reatâncias indutiva e capacitiva ( X L , X C ) a
impedância total ( Z ) a corrente no circuito (I), as quedas de tensão na resistência ( V R ), na
indutância ( V L ) e capacitância ( VC ) a potência ativa total consumida (P) e o fator de potência
( cos( ) ). Desenhe o diagrama fasorial do circuito adotando a tensão aplicada como referência.
Resp.: X L  32 , X C  50 , Z  30  36.9 , I=1A, VR  24V , VL  32V , VC  50V ,
P= 24 W, FP= 0.8 capacitivo.
6
Eletotécnica Aplicada (ETE)- Segunda Lista de Exercícios
R  24
I
V  30V
2 KHz
C  1.59F
~
L  2.55mH
Figura 8. Circuito para o exercício 26.
27) Calcule a impedância total e a corrente do circuito RLC série mostrado na Figura 9. Desenhe o
diagrama fasorial do circuito utilizando a tensão da fonte como referência. Quais as potências
ativa, reativa e aparente totais consumidas. Resp.: Z  35.445o , I=2.82 A. P=200 W,
Q=200VAR, S=282.84 VA.
R1  10
X C1  20
I
V  100V
X C 2  10
~
X L1  30
X L2  25
R2  15
Figura 9. Circuito para o exercício 27.
28) Seja o circuito da figura 10 a seguir. Calcule I T ,  , o fator de potência e Z . Resp.:
I T  7.82 A ,   33.5o , FP  0.834 indutivo , Z  3.07 .
IT
VT  650V
X L1  40
R2  5
R1  30
X C 2  12
~
Figura 10. Circuito para o exercício 28.
7
Eletotécnica Aplicada (ETE)- Segunda Lista de Exercícios
29) Um motor consome 2 KW e 10 A de uma linha de 220V e 60 Hz. Calcule a potência aparente e a
capacitância de um capacitor em paralelo que fará a correção do fator de potência total para 1.
Resp.: S= 916 VA; C=50 μF.
30) Seja o circuito da figura 11 a seguir. Calcule I T ,  , o fator de potência, Z e as potências ativa,
reativa e aparente consumidas pelo circuito. Resp.: I T  4.49 A ,   20.9 o , Z  22.3 ,
FP=0.934, P= 419 W, S=448.60, Q=160.27VAR.
IT
VT  650V
R1  50
X L2  20
~
X L3  110
X C1  70
X C1  50
R2  40
Figura 11. Circuito para o exercício 30.
R1  30