o Seu pé direito na medicina

o Seu pé direito na medicina
UNIFESP – 16/12/2005
FÍSICA
14. Um projétil de massa m = 0,10 kg é lançado do solo com
velocidade de 100 m/s, em um instante t = 0, em uma
direção que forma 53º com a horizontal. Admita que a
resistência do ar seja desprezível e adote g = 10 m/s2.
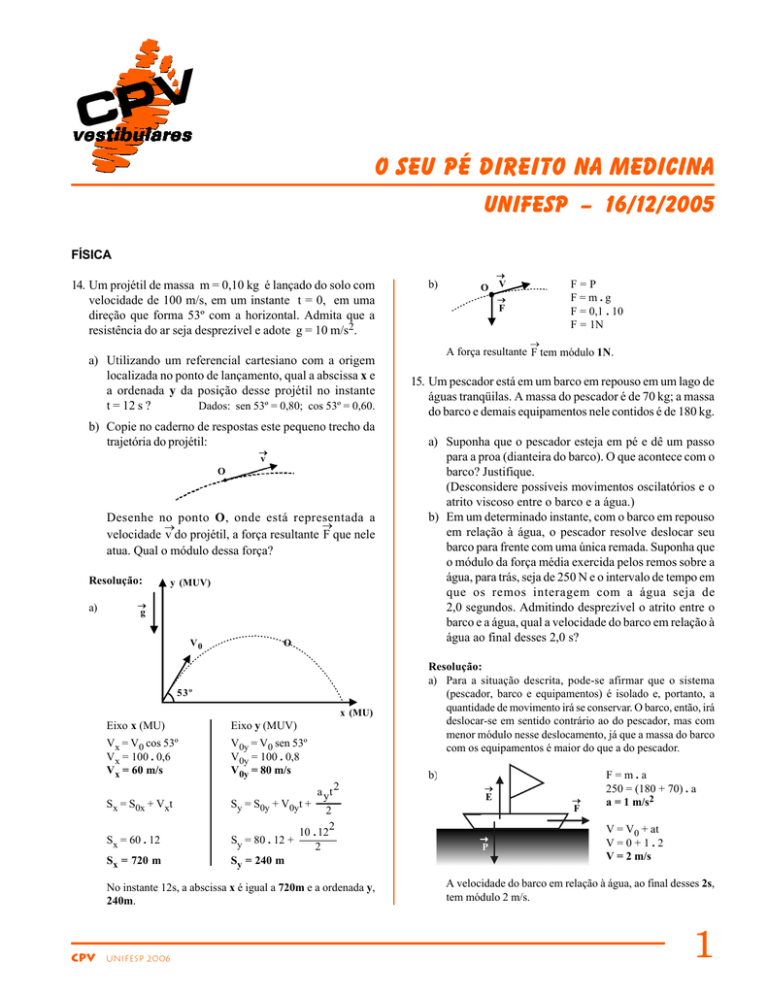
b)
→
O
V
F=P
F=m.g
F = 0,1 . 10
F = 1N
→
F
→
a) Utilizando um referencial cartesiano com a origem
localizada no ponto de lançamento, qual a abscissa x e
a ordenada y da posição desse projétil no instante
t = 12 s ?
Dados: sen 53º = 0,80; cos 53º = 0,60.
b) Copie no caderno de respostas este pequeno trecho da
trajetória do projétil:
→
v
O
Desenhe no ponto O, onde está representada a
→
→
velocidade v do projétil, a força resultante F que nele
atua. Qual o módulo dessa força?
Resolução:
a)
y (MUV)
→
g
V0
O
53º
x (MU)
Eixo x (MU)
Eixo y (MUV)
Vx = V0 cos 53º
Vx = 100 . 0,6
Vx = 60 m/s
V0y = V0 sen 53º
V0y = 100 . 0,8
V0y = 80 m/s
Sx = S0x + Vxt
Sy = S0y + V0yt +
Sx = 60 . 12
Sy = 80 . 12 +
Sx = 720 m
Sy = 240 m
15. Um pescador está em um barco em repouso em um lago de
águas tranqüilas. A massa do pescador é de 70 kg; a massa
do barco e demais equipamentos nele contidos é de 180 kg.
a) Suponha que o pescador esteja em pé e dê um passo
para a proa (dianteira do barco). O que acontece com o
barco? Justifique.
(Desconsidere possíveis movimentos oscilatórios e o
atrito viscoso entre o barco e a água.)
b) Em um determinado instante, com o barco em repouso
em relação à água, o pescador resolve deslocar seu
barco para frente com uma única remada. Suponha que
o módulo da força média exercida pelos remos sobre a
água, para trás, seja de 250 N e o intervalo de tempo em
que os remos interagem com a água seja de
2,0 segundos. Admitindo desprezível o atrito entre o
barco e a água, qual a velocidade do barco em relação à
água ao final desses 2,0 s?
Resolução:
a) Para a situação descrita, pode-se afirmar que o sistema
(pescador, barco e equipamentos) é isolado e, portanto, a
quantidade de movimento irá se conservar. O barco, então, irá
deslocar-se em sentido contrário ao do pescador, mas com
menor módulo nesse deslocamento, já que a massa do barco
com os equipamentos é maior do que a do pescador.
b)
a yt 2
2
10 . 122
2
No instante 12s, a abscissa x é igual a 720m e a ordenada y,
240m.
+28unifesp 2006
A força resultante F tem módulo 1N.
→
E
→
F
→
P
F=m.a
250 = (180 + 70) . a
a = 1 m/s2
V = V0 + at
V=0+1.2
V = 2 m/s
A velocidade do barco em relação à água, ao final desses 2s,
tem módulo 2 m/s.
2
unifesp – 16/12/2005
o seu pé direito na medicina
16. A figura reproduz o esquema da montagem feita por Robert
Boyle para estabelecer a lei dos gases para transformações
isotérmicas. Boyle colocou no tubo uma certa quantidade
de mercúrio, até aprisionar um determinado volume de ar
no ramo fechado, e igualou os níveis dos dois ramos. Em
seguida, passou a acrescentar mais mercúrio no ramo aberto
e a medir, no outro ramo, o volume do ar aprisionado (em
unidades arbitrárias) e a correspondente pressão pelo
desnível da coluna de mercúrio, em polegadas de mercúrio.
Na tabela, estão alguns dos dados por ele obtidos, de
acordo com a sua publicação New Experiments PhysicoMechanicall, Touching the Spring of Air, and its Effects,
de 1662.
b) PA = PB
PAR = PO + PHg
PAR = PO + dHg . g . h
ramo
aberto
coluna de
mercúrio
desnível
ramo
fechado
nível
inicial
pressão
(polegadas de
mercúrio)
pxV
48
29
2
16
1398
40
35
5
16
1413
32
44
3
16
1414
24
58
13
16
1412
16
87
14
16
1406
9
16
1411
12
117
PAR = 3,1 x 105 Pa
desnível
ramo
fechado
A
nível
inicial
B
A pressão do ar aprisionado, para o volume de 24 unidades
arbitrárias, é 3,1 x 105 Pa.
17. Um estudante observa que, com uma das duas lentes iguais
de seus óculos, consegue projetar sobre o tampo da sua
carteira a imagem de uma lâmpada fluorescente localizada
acima da lente, no teto da sala. Sabe-se que a distância da
lâmpada à lente é de 1,8 m e desta ao tampo da carteira é de
0,36 m.
a) Qual a distância focal dessa lente?
b) Qual o provável defeito de visão desse estudante?
Justifique.
Resolução:
a)
a) Todos os resultados obtidos por Boyle, com uma
pequena aproximação, confirmaram a sua lei.
Que resultados foram esses? Justifique.
b) De acordo com os dados da tabela, qual a pressão, em
pascal, do ar aprisionado no tubo para o volume de
24 unidades arbitrárias?
Utilize para este cálculo:
pressão atmosférica p0 = 1,0 x 105 pascal;
densidade do mercúrio dHg = 14 x 103 kg/m3;
g = 10 m/s2;
13
58 16 pol = 1,5 m.
Resolução:
a) De acordo com a Lei de Boyle, o produto pressão x volume
(P x V) de um gás é constante. A terceira coluna da tabela
apresentada confirma a lei, já que o produto P x V mantevese constante (análise executada considerando a pequena
aproximação sugerida no enunciado).
+28unifesp 2006
coluna de
mercúrio
PAR = 1,0 x 105 + 14 x 103 + 10 x 1,5
http://chemed.chem.purdue.edu/genchem/history/
volume
(unidade
arbitrária)
ramo
aberto
1
1
1
=
+
f
P
P'
1
1
1
=
+
f
1,8
0,36
f = 0,3 m ⇒ f = 30 cm
A distância focal da lente é 30 cm.
b) Como o estudante usa lentes convergentes (f > 0), o seu
provável defeito de visão é a hipermetropia.
18. Quando colocamos uma concha junto ao ouvido, ouvimos
um “ruído de mar”, como muita gente diz, talvez imaginando
que a concha pudesse ser um gravador natural. Na verdade,
esse som é produzido por qualquer cavidade colocada junto
ao ouvido — a nossa própria mão em forma de concha ou
um canudo, por exemplo.
a) Qual a verdadeira origem desse som? Justifique.
b) Se a cavidade for um canudo de 0,30 m aberto nas duas
extremidades, qual a freqüência predominante desse
som?
Dados:
velocidade do som no ar: v = 330 m/s;
freqüências de ondas estacionárias em um tubo de
nv
comprimento l, aberto em ambas as extremidades: f =
2l
O seu pé direito na medicina
Resolução:
a) O som tem origem com a perturbação do ar no interior da
cavidade. O movimento das moléculas de ar dentro de uma
concha ou um canudo formam as ondas sonoras.
b) Freqüência predominante (fundamental): n = 1.
Como: f =
1 . 330
nV
⇒ f = 2 . 03 ⇒ f = 550 Hz
2l
unifesp – 16/12/2005
COMENTÁRIO DA PROVA DE FÍSICA
A prova foi bem elaborada com os temas bem distribuídos e o
nível de dificuldade esperado.
DISTRIBUIÇÃO DAS QUESTÕES
A freqüência predominante do som é 550 Hz.
19. Para demonstrar a interação entre condutores percorridos
por correntes elétricas, um professor estende paralelamente
dois fios de níquel-cromo de 2,0 mm de diâmetro e
comprimento l = 10 m cada um, como indica o circuito
seguinte.
l
níquel-cromo
2,0 cm
A
E
a) Sendo ρNi-Cr = 1,5 x 10–6 Ω . m a resistividade do
níquelcromo, qual a resistência equivalente a esse par
de fios paralelos? (Adote π = 3)
b) Sendo i = 2,0 A a leitura do amperímetro A, qual a força
de interação entre esses fios, sabendo que estão
separados pela distância d = 2,0 cm? (Considere
desprezíveis as resistências dos demais elementos do
circuito.)
Dada a constante de permeabilidade magnética:
µ0 = 4π x 10–7 T . m/A.
Resolução:
a) A resistência R de cada fio é dada por:
R=ρ
l
A
⇒ R=
1,5 x 10
−6
x 10
⇒ R = 5Ω
3
−
π . (10 )2
A resistência equivalente REQ é dada por:
R
⇒ REQ = 2,5 Ω
2
A resistência equivalente a esse par de fios é 2,5 Ω.
REQ =
b) O módulo do campo magnético gerado por um fio é dado por:
B=
−7
M0 . i
4π x 10 . 1
⇒ B=
⇒ B = 1 x 10–5 T
2π . d
2
−
2π . 2 x 10
O módulo da força magnética atuando nos fios é dado por:
FM = B . i . L sen θ ⇒ FM = 1 x 10–5 . 1 . 10 . sen 90º
FM = 1 x 10–4 N
O módulo da força de interação entre os fios é 1 x 10–4 N.
+28unifesp 2006
Eletrodinâmica
8%
Eletromagnetismo
8%
Mecânica
33%
Ondas
17%
= 10m
níquel-cromo
3
Termologia
17%
Óptica
17%