Lista de exercícios - Regra de Kirchhoff

Lista de exercícios - Regra de Kirchhoff
Circuitos Complexos – Regra de Kirchhoff
Existem alguns circuitos em que não é possível fazer a separação de partes em
série e/ou em paralelo e além disto podem ter mais de uma fonte (um carregador
de baterias por exemplo).
Nestes casos usam-se um conjunto de regras (ou leis) e definições criadas por um
físico alemão chamado Kirchhoff.
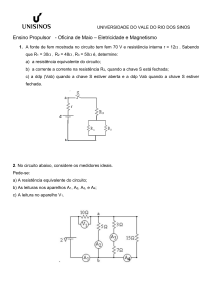
O circuito ao lado possui dois nós e
três malhas.
Nós: os pontos marcados pelas letras
A e B.
Malha 1: E1, R1, RL; Malha 2: E1, R1, R2,
E2; Malha 3: E2, R2, RL.
Definições:
- Nó: é todo ponto de junção, amarração de condutores.
- Malha: é todo caminho fechado percorrido no circuito.
Leis:
-
-
Nós: a soma das correntes que chegam em um nó e igual a soma das
correntes que saem deste nó. Esta lei é consequência da conservação da
carga elétrica, que não pode ser criada ou destruída.
Malhas: a soma das FEM e das quedas de tensões nos resistores é
sempre igual a zero. Esta lei é consequência da conservação da energia,
pois toda energia fornecida por uma fonte de FEM vai ser consumida
pelo elementos resistivos.
Convenção de Sinais: quando percorremos um circuito o caminho pode ser
horário ou anti-horário e não precisa coincidir com o sentido de circulação da
corrente. Este fato é importante na atribuição de sinais às tensões das baterias (ε)
e das quedas de tensões nos resistores (RI):
- Baterias: se ao percorrermos uma malha o percurso passar do pólo
positivo para o pólo negativo da bateria usamos –ε (o potencial
diminui); caso contrario usa-se +ε (o potencial aumenta).
- Resistores: se ao percorrermos uma malha o percurso passar pelo
resistor no mesmo sentido da corrente usamos –RI; caso contrario usase +RI.
Importante: ao se resolver as equações pode-se encontrar um resultado negativo
para a corrente; não há nenhum problema nesta situação. Trabalha-se com este
resultado durante todo o restante da resolução, deve-se apenas lembrar que na
verdade a corrente circula no sentido oposto ao que se escolheu inicialmente.
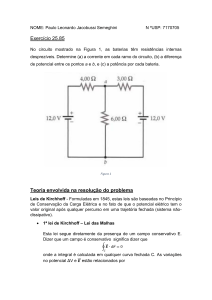
EXEMPLO 1: Um circuito com uma única malha O circuito indicado contém dois
resistores e duas baterias, cada uma delas com uma fem e uma resistência interna.
Calcule: a) a corrente no circuito; b) a diferença de potencial Vab e c) a potência de cada
fem.
(a) Neste exemplo percorremos a malha do circuito no
mesmo sentido que escolhemos para a corrente, de modo
que os termos IR são negativos. O potencial diminui
quando você atravessa a fem inferior do + para o -,
porém aumenta quando você atravessa a fem na parte
superior do - para o +. (b) Um exemplo real de um
circuito do tipo aqui analisado
SOLUÇÃO Trata-se de um circuito simples com uma única malha e que não possui
nenhum nó, portanto não precisamos da lei dos nós de Kirchhoff. Para aplicarmos a lei
das malhas a esse circuito com uma única malha, escolhemos inicialmente um sentido
para a corrente. Vamos eleger o sentido anti-horário, conforme indicado. A seguir,
partindo do ponto a, percorra a malha no sentido anti-horário, faça a soma algébrica de
todas as diferenças de potencial ao longo do percurso e iguale o resultado a zero. Você
obterá a seguinte equação:
-I.(4Ω) - 4V – I.(7Ω) + 12 V - I(2Ω) - I(3Ω) = 0. Agrupando os termos que contêm I e
explicitando I, encontramos
8V = I.(l6Ω)
I= 0,5 A.
O resultado obtido para I é positivo, o que mostra que o sentido escolhido para a
corrente é correto. Como exercício, escolha o sentido contrário para I e resolva
novamente a equação; você deverá encontrar I = -0,5 A, o que indica que o sentido real
da corrente é contrário ao escolhido.
b) Para calcularmos Vab, a diferença de potencial de a em relação a b, partimos do ponto
b e fazemos a soma algébrica de todas as diferenças de potencial até chegar ao ponto a.
Existem dois percursos para ir de b até a; usando o percurso inferior, obtemos
Vab = (0.5 A)(7Ω) + 4 V + (0.5 A)(4Ω) = 9.5 V.
O ponto a possui um potencial 9,5 V mais elevado do que o potencial do ponto b.
Todos os termos dessa soma, incluindo os termos IR, são positivos porque cada um
deles representa um aumento quando vamos de b até a. Considerando o percurso
superior, encontramos
Vab = 12 V - (0,5 A)(2Ω) - (0,5 A)(3Ω) = 9,5 V.
Na relação anterior, os termos IR são negativos porque o sentido do percurso é o
mesmo da corrente, o que provoca uma diminuição de potencial ao atravessarmos
cada resistor.
O resultado obtido é o mesmo nos dois percursos, como era esperado, uma vez que a
variação total da diferença de potencial ao longo do circuito completo deve ser igual a
zero.
c) A potência fornecida pela fem da bateria de 12 V é
V)(0,5 A) = 6 W,
e a potência da bateria de 4 V é
P =εI = (-4 V)(0,5 A) = -2 W.
P = εI = (12
O sinal negativo de é da bateria de 4 V surge porque a corrente percorre a bateria do
terminal com potencial mais elevado para o terminal com potencial mais baixo. O valor
negativo de P indica que a bateria consome potência porque está armazenando energia
na bateria e está sendo recarregada pela bateria de 12 V. O circuito indicado é
semelhante ao usado no caso real quando uma bateria de automóvel de 12 V carrega a
bateria de outro automóvel que estava descarregada. Os resistores de 3Ω e de 7Ω na
representam os cabos condutores e os conectores usados para ligar as duas baterias
(embora os valores das resistências no exemplo real não sejam exatamente iguais aos
desse exemplo numérico).
EXEMPLO 2: Carregando uma
bateria O circuito indicado na
Figura 3 contém uma fonte de
tensão de 12 V com resistência
interna desconhecida r conectada
com uma bateria descarregada com
fem ε e resistência interna igual a
1Ω e com uma lâmpada de
resistência de 3Ω que transporta
uma corrente de 2A. A corrente que
passa na bateria descarregada é
igual a 1A no sentido indicado.
Calcule a resistência interna
desconhecida r, a corrente I e a fem
ε.
SOLUÇÃO
Inicialmente, aplicamos a lei dos nós ao ponto a. Encontramos:
- I + 1A + 2A = 0;
logo, I = 3 A.
Para determinarmos r, aplicamos a lei das malhas para a malha. externa designada por
(1); obtemos
12 V - (3A)r - (2A)(3Ω) = 0;
logo, r = 2Ω.
Os termos com as resistências r e 3Ω são negativos porque o sentido do percurso através
desses elementos é o mesmo sentido da corrente e, portanto, existe uma queda de
potencial em cada um desses elementos. Caso resolvêssemos percorrer a malha externa
(1) no sentido contrário, todos os termos teriam sinais opostos, e o resultado obtido para
r seria o mesmo.
Para determinarmos ε, aplicamos a lei das malhas para a malha designada por (2):
- ε + (lA)(1Ω) - (2 A)(3Ω) = 0;
logo, ε = -5 V.
O termo do resistor de 1Ω é positivo porque, ao atravessá-lo no sentido oposto ao da
corrente, ocorre um aumento do potencial. O valor negativo de ε mostra que a
polaridade real dessa fem é oposta à indicada na figura; o terminal positivo dessa fonte
está, na realidade, do lado direito. Como indicado no exemplo anterior, a bateria está
sendo recarregada. Alternativamente, poderíamos usar a malha (3) e obter a equação
12 V - (3A)(2Ω) - (1A)(lΩ) + ε = 0,
que ε = -5 V.
a partir da qual concluímos novamente
Para uma verificação adicional da consistência do resultado, notamos que Vba = Vb - Va
é igual à tensão através do resistor de 3Ω dada por (2A)(3 ε) = +6 V. Percorrendo o
ramo da malha superior de a para b, encontramos a diferença de potencial +12 V (3A)(2Ω) = +6 V e percorrendo o ramo central obtemos -(-5V) + (l A)(lΩ) = +6 V. As
três maneiras de calcular Vba forneceram os mesmos resultados. Verifique se você
entendeu todos os sinais dos cálculos anteriores.
EXERCÍCIOS
1. No circuito indicado na figura desta questão, calcule: a) a corrente no resistor R; b)
a resistência R; c) a fem desconhecida ε.
2. Calcule a fem εl e a fem ε2 no circuito da figura e a diferença de potencial do ponto
b em relação ao ponto a. (Va – Vb).
3. No circuito indicado na figura, calcule a) a corrente no resistor de 3,00 Ω; b) a fem
ε1 e a fem ε2; c) a.resistência R. Observe que foram fornecidas três correntes.
.
4. No circuito indicado, determine: a) a corrente em cada ramo; b) a diferença de
potencial Vab do ponto a em relação ao ponto b.
RESPOSTAS
1. IR = 2,0 A (no sentido do polo negativo da bateria (28 V) para o polo
positivo)
R=5Ω
ε = 42 V
2. ε1 = 18, 0 V
ε2 = 7,0 V
3. I3Ω = 8,00 A (de baixo para cima)
ε1 = 36, 0 V
ε2 = 54,0 V
R = 9Ω
4. I3Ω = 0,8 A (no sentido do polo negativo da bateria (10 V) para o polo
positivo)
I4Ω = 0,2 A (no sentido do polo positivo da bateria (5 V) para o polo
negativo)
I10Ω = 0,6 A (da esquerda para a direita)
Vab = -3,2 V
I10Ω = 0,2 A (da direita para a esquerda)
Vab = 10,4 V