prova de máquinas cc

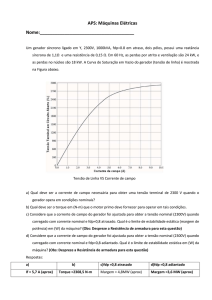
Resolução da questão 3
Para responder essa questão é necessário verificar que o motor já está operando e que
em determinado momento algum grandeza do motor irá variar. Frente a essa variação,
deve-se determinar o comportamento da corrente de armadura e da velocidade. Para
ficar claro, verifique como foi respondida a letra (a).
a)
Conforme figura acima, tem-se que a força contra-eletromotriz induzida inicial (ainda
não ocorreu nenhuma variação de determinada grandeza, como a tensão de armadura
por exemplo) do motor é dada por:
E A VA
I A RA
(1)
E que a força contra-eletromotriz é dada por:
EA
KФω
(2)
Considerando que a queda de tensão na armadura é desprezível (conforma observação
feita na própria questão), então as equações (1) e (2) tornam-se respectivamente em:
E A VA
VA
KФω
(3)
(4)
Lembre-se que VA é a tensão terminal de armadura devido ao circuito conversor (CC –
CC) que varia a tensão aplicada ao enrolamento de armadura.
Com base na questão, a tensão de armadura foi reduzida à metade. Chamarei essa nova
tensão de V An , enquanto a corrente de campo e a potência da carga permanecem
constantes.
Então se tem que:
VAn
VA
2
(5)
A nova força contra-eletromotriz é dada por:
VAn
KФωn
(6)
Observe que fluxo permanece constante, por isso que não teve um novo indicador.
Dividindo a equação (4) pela equação (6) resulta em:
VA
VAn
KФω
KФωn
(7)
Substituindo (5) em (7) resulta em:
ωn
ω
2
(8)
Significa, portanto que a velocidade foi reduzida à metade.
Agora o que acontece com a corrente de armadura?
Utilizaremos para isso a fórmula do torque e o fluxo de potência na máquina. Uma
breve explanação. Na operação da máquina como motor elétrico, a potência de entrada é
de natureza elétrica. Uma parte dessa potência é perdida nos condutores e a parcela
restante é denominada de potência mecânica desenvolvida (“convertida”) dada pela
seguinte fórmula:
EAI A
τ des ω
(9)
Em que τ des é o torque desenvolvido que não está disponível no eixo do motor caso seja
considerada a existência de perdas mecânicas e no núcleo. Para nossa análise,
desprezaremos essas perdas e consideraremos que toda potência interna desenvolvida
corresponde à potência de saída (potência da carga). Portanto, o torque desenvolvido
corresponde ao torque da carga.
Podem existir outras formas para analisar essa questão, mas a seguinte acho mais de
entender. Sabemos que o torque depende do fluxo e da corrente de armadura, então:
IA
τ
KФ
(10)
Esse torque τ corresponde o torque da carga que por questão de simplificação é igual ao
torque desenvolvido. Como não há variação nem no torque e nem no fluxo, a corrente
permanece constante.
Essa foi a explicação da letra (a). As outras letras possuem raciocínios semelhantes.
(b) Para essa questão as algumas simplificações também podem ser feitas. As grandezas
já foram definidas na letra (a).
Sabendo que a potência mecânica desenvolvida inicial é dada por:
Pdes
EAI A
τω
(1b)
E considerando que a equação (3) é válida também aqui. Então, para a nova situação
tem-se que:
Pdes
E An I An
(2b)
Sabendo-se que a potência da carga permanece constante, então (1b) é igual a (2b). As
equações (3) e (5) da letra (a) devem ser utilizadas para chegar à resposta final. Vocês
podem utilizá-las para chegar à resposta final.
I An
2I A
Tentem encontrar o que ocorre com a velocidade. A resposta é que ela é reduzida à
metade. Dica: utilize a equação (4) da letra (a) para encontrar a resposta.
c) Para encontrarmos o que acontece com a corrente de armadura, podemos utilizar a
fórmula do torque desenvolvido dada pela equação (10) da letra (a). Na situação inicial,
o torque é dado por:
τ
KФI A
(1c)
Foi abordado na questão que o fluxo de campo variou (dobrou), mas tensão de armadura
e conjugado (torque) da carga permanece constante. Então, podemos chegar à conclusão
que corrente de armadura deve variar, de maneira que o produto fluxo pela corrente de
armadura permaneça o mesmo. Então, que o torque também pode ser dado por:
τ
KФn I An
(2c)
O novo fluxo é dado por:
Фn
2Ф
(3c)
Manipulando as equações (1c), (2c) e (3c) resulta em:
I An
IA
2
(4c)
Para encontrar como a velocidade varia pode utilizar a equação (4) da letra (a). A
resposte é que a nova velocidade é a metade da anterior.
d) Nesse caso temos que:
Фn
V
n
A
Ф
2
VA
2
(1d)
Em que V An é a nova tensão de armadura como foi abordada na letra em questão.
Então para duas situações, escrevemos as forças contra-eletromotrizes:
VA
KФω
(2d)
VAn
KФn ωn
(3d)
OBS: Verificar letra (a) para acompanhar como chegamos
nestas duas equações. Desprezamos a queda de tensão no
enrolamento de armadura (IARA).
Fazendo as substituições da equação (1d) em (2d) e em (3d) resulta a seguinte
conclusão.
ωn
ω
(4d)
Não ocorre variação na velocidade.
Para encontrar o que acontece com a corrente de armadura, podem utilizar a fórmula da
potência desenvolvida. A corrente de armadura dobra o seu valor.
I An
2I A
e) Vocês são capazes de responder com base nas explicações anteriores.
A velocidade cai à metade e corrente é reduzida por um fator 4.
6)
a) Na condição sem carga, o torque aplicado pela máquina primária (turbina a gás,
hidráulica, motor a diesel) no eixo do gerador é necessário para vencer as perdas no
gerador. Fazer fluxo de potência para entender a questão. O torque aplicado pela
máquina primária e a potência de entrada são relacionados pela seguinte fórmula:
Pent
τ ap ωm
(1)
Em que:
Pent - potência de entrada do gerador (potência mecânica)
τ ap - torque aplicado pela máquina primária no eixo do gerador
ω m - velocidade de rotação do gerador
Com os dados da questão, podemos calcular a potência de entrada.
Pent
τ ap ωm
47,1.1800.
2 pi
60
8878watts
(2)
Sem carga, a potência de saída é zero de maneira que toda potência de entrada é para
suprir as perdas.
Podemos escrever a potência de entrada da seguinte forma:
Pent
Pmec
Pnucleo
R f I 2f
Em que:
Pmec - perdas mecânicas
Pnucleo - perdas no núcleo
R f I 2f - perdas no circuito de campo
(3)
A corrente de campo calculada aqui é a partir da tensão a vazio (445 V).
As perdas mecânicas mais as perdas no núcleo são denominadas de perdas rotacionais
Prot .
As perdas rotacionais podem ser calculadas a partir da equação (3).
Prot
6238watts
b) Perdas no cobre
As perdas no cobre compreendem duas parcelas: perdas no circuito de armadura e as
perdas no circuito de campo.
RA I A2
Pcobre
R f I 2f
(4)
10535,76watts
A corrente de armadura pode ser encontrada somando-se a corrente de linha a plena
carga com a corrente de campo.
IA
If
IL
5,93 400
405,6 A
(5)
A corrente de linha I L foi fornecida na questão e é igual a 400 A. E I f é dada por:
VT
75
If
416
75
5,55 A
(6)
c) A potência de saída do gerador a plena carga
Psaida
VT . I L
416.400 166400watts
(7)
d) A eficiência do gerador a plena carga
η
Psaida
Pent
Psaida
Psaida
Pcobre
Prot
166400
166400 10535,7 6238
166400
183173.7
90,8%
(8)
e) Cálculo do torque desenvolvido a plena carga
Com base no fluxo de potência para o gerador, a potência desenvolvida (convertida de
mecânica para elétrica) é dada por:
Pdes
Psaida
Pcobre
166400 10535,7 176935,7 watts
(9)
O cálculo do torque desenvolvido é dado por:
τ des
Pdes
ωm
176935,7
188,5
938,66 N .m
(10)
Esse torque se opõe direção de rotação, ou seja, se opões ao torque aplicado pela
máquina primária.
O torque aplicado pela máquina primária a plena carga relaciona a potência de entrado
no gerador com a velocidade.
τ ent
Pent
ωm
183173,7
188,5
971,74 N .m