Equação de Dirac com campo magnético

Eq. de Dirac com campo magnético
Rafael Cavagnoli
GAME: Grupo de Médias e Altas Energias
Eletromagnetismo clássico
● Eq. de Schrödinger
● Partícula carregada em campo mag.
● Eq. de Dirac
● Partícula carregada em campo mag.
●
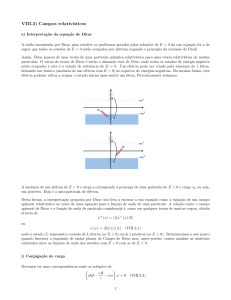
Partícula em campo magnético
O campo magnético não altera a energia cinética do sistema
(=> campo elétrico, pois WB =0), contudo altera a direção da velocidade
(e do momentum linear):
⃗F = q E⃗ l +q ⃗v × ⃗B
Se E = 0 temos um movimento circular (freq. de cíclotron):
|q| B
m
Vamos escrever a hamiltoniana do sistema, ao invés de trabalhar com a
Força de Lorentz.
ωc =
H = K + U
Do modelo de Bohr:
L = nℏ
Então para n = 1, no caso de um elétron no nível fundamental:
eℏ
μB =
2 me
(magneton de Bohr)
Precessão de Larmor:
μB
⃗L
μ⃗l = −
ℏ
μ B = 0,927×10−23 A m2 = 5,788×10−5 eV /T
ωL =
|q| B
2m
Em termos do potencial eletrostático:
⃗V
E⃗l = − ∇
U el = q V (r)
De maneira análoga:
U mag = − B⃗ ⋅ μ⃗
U mag
q ⃗ ⃗
= −
B⋅ L
2m
Hamiltoniana:
H = K + U
2
^
p
H^ =
+ U^ (r ) + U^ mag
2m
Partícula livre carregada em campo E e B
⃗A
∂
⃗V
⃗El = −
− ∇
∂t
;
⃗ × ⃗A
⃗B = ∇
Neste caso V não é mais eletrostático.
Etot
1
2
= m ⃗v + q V
2
⃗ptot = m ⃗v + q ⃗A
Usando o princípio da correspondência (clássico → quântico):
^H = 1 p^ 2 + q V^
2 m cin
⃗ = ^p + q A
^
^ptot = −i ℏ ∇
cin
^ − q A^
^p cin = −i ℏ ∇
^H = 1 ^p 2 + q V^
2 m cin
^H = 1 [−i ℏ ∇ −q A]2 + q V^
2m
Partícula livre e carregada sob influência de campos elétrico e
magnético, caso não-relativístico.
H^ Ψ = E Ψ
⃗
p → −i ℏ ∇
⃗ −q A
p → −i ℏ ∇
;
E → iℏ ∂
∂t
Elétron livre num campo magnético uniforme
Podemos escrever o potencial vetor na forma:
tal que:
⃗A = (0 , B 0 x , 0) = B 0 x ^j
⃗ × ⃗A =B k^
⃗B = ∇
0
Hamiltoniana (com V = 0, pois E = 0):
^H = 1 [−i ℏ ∇ −q A]
^ 2
2m
^H = 1 [ ^p +e B 0 ^x ^j]2
2m
^H = 1 [ ^p2 + e B ^p x^ ^j + e B x^ ^j ^p + e 2 B 2 x^ 2 ]
0
0
0
2m
^H = 1 [ ^p2 + e B p^ x^ + e B ^x p^ + e2 B 2 ^x 2 ]
0 y
0
y
0
2m
Lembrando que:
[ xi , pi ] = i ℏ δij
;
[ x , py] = 0
;
p y =−i ℏ ∂
∂t
1 2
H^ =
[ p + 2 e B0 p y x + e 2 B02 x 2 ]
2m
Também temos que:
d ^
i ^ ^
∂ O^
⟨ O⟩ = ⟨[ H , O]⟩ +
dt
∂t
ℏ
( )
Se comuta com H, < O > é cte no tempo, há uma grandeza cujo valor
esperado é conservada; também forma uma base com H; autofunções...
^H = 1 [ p 2 + p 2 + p 2 + 2 e B p x + e 2 B 2 x 2 ]
y
z
0 y
0
2m x
^H = 1 [ p 2 + p 2 + ( p + e B x )2 ]
z
y
0
2m x
2
[
i
e
B
−ℏ
0
∂
∂
∂
H^ =
+
+
+
x
2
2
2m ∂ x
∂y
ℏ
∂z
2
2
(
)]
2
Fazemos:
[ pi , H ] =
1
2 2
2
2
2
e
B
(
p
x
p
−x
p
p
)
+
e
B
(
p
x
−x
p i) ]
[
0
i
y
y i
0
i
2m
pi x p y −x p y pi = [ pi , x p y ] = −x [ p y , pi ]−[ x , pi ] p y
encontramos que py e pz comutam com H...
Podemos escrever:
Ψ( x , y , z ,t ) = A e (i ⃗p⋅⃗r −Et )/ℏ
pi = ℏ k i
Tomando a parte espacial, e escrevendo
Ψ( x , y , z) = Ψ(x ) e i k y ei k z
y
z
Com o hamiltoniano obtido anteriormente:
2
[
^H = −ℏ ∂ + ∂ + ∂ + i e B0 x
2 m ∂ x2
∂y
ℏ
∂ z2
2
2
(
podemos aplicar em:
H^ Ψ = E Ψ
obtendo:
)]
2
[
2
2
2
2
0
2
]
(
2 2
z
e B0
e B x
ℏ k
−ℏ ∂
ℏ 2
+
ky +
x ℏ ky+
Ψ (x ) = E −
2
2m ∂x
2m
m
2m
2m
2
)
Ψ( x)
a qual podemos escrever como:
[
]
mω 2c
−ℏ2 ∂2
2
+
(
x
−
x
)
Ψ (x ) = E ' Ψ (x )
0
2
2m ∂x
2
que tem a forma da equação para o oscilador harmônico quântico ☺
(centrado em x0), com frequência ωc sendo:
logo:
ℏk y
py
x0 = −
= −
e B0
e B0
;
1
E '=E n= n+
ℏ ωc
2
( )
com n = 0,1,2,3,...
e B0
ω c=
m
Neste caso podemos escrever:
p2z
1
En =
+ n+
ℏ ωc
2m
2
( )
onde n representa os níveis de Landau.
(x0 não comuta com y, o centro da “órbita” tem coordenada y que não é bem definida, ky
ou py é limitado pelo sistema)
Caso relativístico – eq. de Dirac
- descreve férmions de spin ½
- energia relativística
- quadri-vetores
- invariância de Lorentz
2
2 2
2 4
E = p c + mc
usando unidades naturais (c = h = 1)
E2 = p 2 + m 2
onde:
pμ = (p 0 , ⃗p ) = ( E/c , ⃗p )
Através de:
^
^p → −i ℏ ∇
;
E^ → i ℏ ∂
∂t
Novamente usando:
H Ψ = EΨ
obtém-se:
2
2 2
2
2 4
∂
−ℏ Ψ2 = −ℏ c ∇ Ψ + m c Ψ
∂t
2
que é a equação de Klein-Gordon, sendo posteriormente verificado que
descreve partículas de spin 0.
Buscando uma equação linear em t, respeitando a energia
relativística, Dirac então seguiu por outro caminho.
Lembrando que:
pμ pμ = m 2 c 2
⇒
2
2 2
2 4
E = p c + mc
pμ pμ−m2 c 2 = 0
Dirac propôs:
pμ pμ −m2 c 2 = (βi p i +mc)(γ j p j−m c) = 0
2 2
μ
κ
λ
p pμ−m c = (β p κ +mc)(γ p λ −mc ) = 0
que fica:
κ
λ
κ
κ
2 2
β γ p κ pλ − m c (β − γ ) p κ − m c = 0
Para resultar em:
pμ pμ−m2 c 2 = 0
κ
κ
basta determinar β , γ . Como não interessam termos lineares em p i,
significa:
κ
κ
β = γ
κ
λ
2 2
γ γ pκ pλ − m c = 0
pμ pμ = γ κ γ λ pκ p λ
Abrindo a expressão acima, obtemos que os gamas são matrizes 4x4.
1
0
0
γ =
0
0
(
0 0 0
1 0 0
0 −1 0
0 0 −1
)
(
0 σ
γ =
i
−σ 0
i
,
i
)
onde as matrizes de Pauli são dadas por:
1
σ =
( )
0 1
1 0
2
, σ =
(
0 −i
i 0
)
3
, σ =
Deste modo, a equação:
(βκ p κ + mc)( γλ pλ − m c) = 0
Pode ser escrita como:
μ
μ
(γ pμ + mc)(γ pμ − mc ) = 0
(
1 0
0 −1
)
de onde obtemos:
μ
(γ pμ − m c ) = 0
Voltando a usar a equação de autovalores e autofunções:
H Ψ = EΨ
chegamos em:
μ
(i ℏ γ ∂μ − m c )Ψ = 0
sendo agora:
e
eq. de Dirac
ψ1
Ψ = ψ2
ψ3
ψ4
()
1 ∂
∂
∂μ =
, ∇i
μ =
∂x
c ∂t
(
)
Podemos escrever:
q μ
p → p − A
c
μ
μ
Na eq. de Dirac, de modo análogo ao efetuado na eq. de Schödinger:
μ
[γ pμ − m c ]Ψ = 0
resulta em:
[
]
q
γ ( pμ − Aμ ) − mc Ψ = 0
c
μ
Em unidades naturais ( c = h = 1 , sendo massa e momentum em MeV)
ou
[ γμ ( pμ
μ
− q Aμ ) − m ] Ψ = 0
[γ (i ∂μ − q Aμ ) − m]Ψ = 0
Eq. de Dirac em campo magnético
►►►Na verdade usamos a eq. de Dirac para uma partícula livre com
spin ½ e carga elétrica 'q' na presença de um campo magnético.
μ
(i ℏ γ ∂μ − m c )Ψ = 0
De modo geral (com campo El e B):
μ
A = (cV , ⃗A )
agora temos quadri-potencial:
1
q⃗
p =
(E−cV ) , ⃗p − A
c
c
e o quadri-momentum:
μ
sem campos:
μ
p =
E
, ⃗p
c
( )
⇒
q⃗
p →p − A
c
i
i
(
,
0
0
p → p −V
)
Abrindo a eq.
Na ausência de campo elétrico ( A0 = 0)
onde:
ψ1
u
Ψ = ψ2 = A
ψ3
uB
ψ4
()
Precisamos resolver a eq. de autovalor:
()
Para um campo uniforme na direção z, escolhemos:
⃗B = B k^
e em termos do quadri-potencial eletromagnético:
Assim:
Usando as regras de comutação:
obtemos:
sendo o último termo:
Então:
Dando origem a duas equações por causa de σz
As coordenadas x0 [t], x e z não aparecem explicitamente, suas soluções
podem ser escritas como ondas planas. Assim podemos fazer:
As duas equação se diferenciam pelos autovalores da matriz σz, ou seja
s = ± 1. Usando regras de comutação para operadores p, podemos
escrever as duas equações como:
Fazendo uma substituição de variáveis:
Então:
Reescrevendo:
d2 Fs
dξ
2
β
+ α − ξ2 F s = 0
(
)
☺ Esta equação possui a mesma forma da equação para o oscilador
harmônico quântico. ☺
Livro do Eisberg:
FIM !
Obrigado.
Assim, para que a solução exista temos a seguinte condição:
e os autovalores da energia passam a ser:
Tendo então que analisar os autovalores em função de l e s .
⃗p = ℏ ⃗k , (ℏ=c=1 → ⃗p = ⃗k )
Exemplos:
● l=0 e s=1
=>
● l = 0 e s = -1
● l=1 e s=1
=>
=>
E =
E =
2
2
m
+
p
√
z
2
2
m
+
p
√
z +2|e|B
Por causa da degenerescência, podemos escrever a energia de um
férmion de spin ½ num campo magnético uniforme em função de um
único parâmetro:
E =
2
2
m
+
p
√
z + 2 ν |e| B
onde ν representa os níveis de Landau.
Próximo passo: estudar a densidade de estados para um gás de Férmi.
FIM !
OBRIGADO!!!
Alguns Links:
http://images.slideplayer.com.br/2/359061/slides/slide_4.jpg
http://www.usc.es/export/sites/default/gl/investigacion/riaidt/rm/rmn/imaxes/peonza.jpg
http://2.bp.blogspot.com/-yl_CgPaCG8U/ThyU_db4VSI/AAAAAAAAR8/Nu1X19gjnfg/s1600/precesion+en+presencia+de+campo+magnetico.png