Linhas de Transmissão - if

Prof. Márcia R. Gallas (FIS01059)
Linhas de Transmissão
1. Objetivo
Medir a capacitância, indutância e a impedância num cabo coaxial. Observar a
propagação e reflexão de pulsos em cabos coaxiais.
2. Introdução
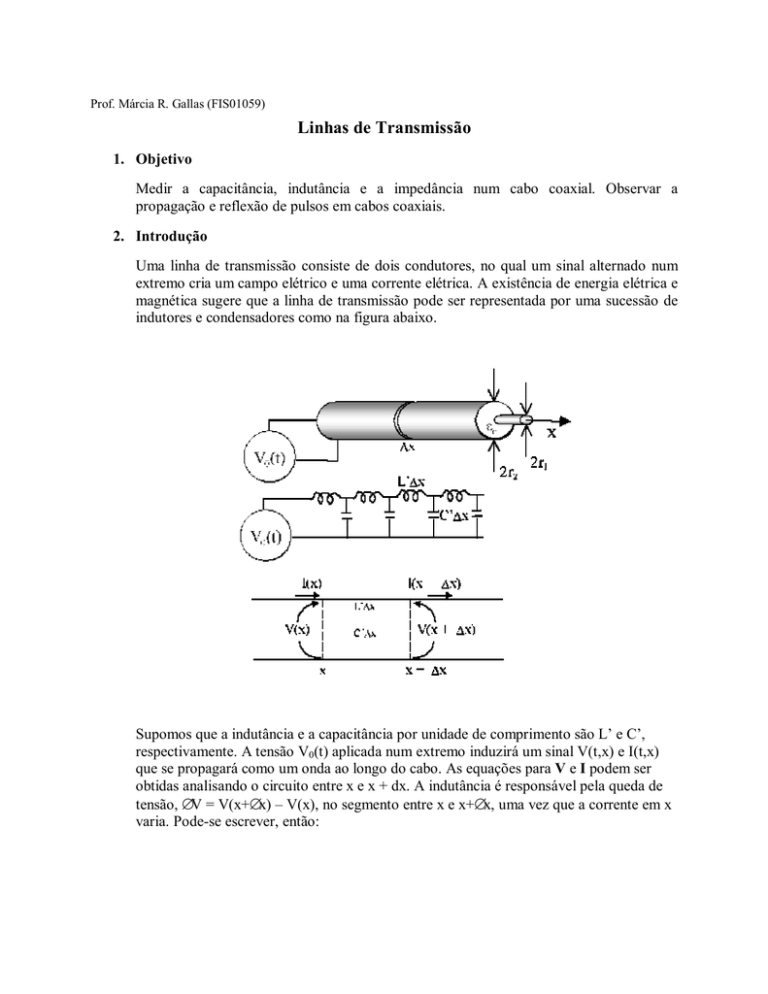
Uma linha de transmissão consiste de dois condutores, no qual um sinal alternado num
extremo cria um campo elétrico e uma corrente elétrica. A existência de energia elétrica e
magnética sugere que a linha de transmissão pode ser representada por uma sucessão de
indutores e condensadores como na figura abaixo.
Supomos que a indutância e a capacitância por unidade de comprimento são L’ e C’,
respectivamente. A tensão V0(t) aplicada num extremo induzirá um sinal V(t,x) e I(t,x)
que se propagará como um onda ao longo do cabo. As equações para V e I podem ser
obtidas analisando o circuito entre x e x + dx. A indutância é responsável pela queda de
tensão, ∆V = V(x+∆x) – V(x), no segmento entre x e x+∆x, uma vez que a corrente em x
varia. Pode-se escrever, então:
Prof. Márcia R. Gallas (FIS01059)
(1)
A tensão ao longo de x também varia em função da carga acumulada pela capacitância na
região ∆x. A carga acumulada ao longo da linha é dada pela diferença de corrente ∆I =
I(x+∆x) – I(x), resultando para estas variações:
(2)
É fácil verificar que a corrente I e a tensão V satisfazem a equação de onda
com velocidade de propagação:
A capacitância e a indutância por unidade de comprimento estão relacionadas com
parâmetros geométricos dos cabos coaxiais.
[OBS: se o meio não for vácuo, ε 0 deve ser substituído por ε R (=kεε 0)]
Uma tensão V0(t) aplicada num extremo desta linha de transmissão gera uma onda dada
por:
(3)
A corrente induzida também possui a forma:
(4)
A relação entre V0 e I0 é obtida substituindo numa das equações acima (1) ou (2), a
tensão e a corrente dadas em (3) e (4), respectivamente, e integrando, desprezando a
constante de integração arbitrária. A relação entre a tensão e corrente de uma onda que se
desloca na direção positiva do eixo x será, portanto:
Prof. Márcia R. Gallas (FIS01059)
O quociente entre a tensão e a corrente é a impedância Z da linha de transmissão, dada
por:
(6)
Para um pulso de tensão que se propaga na direção negativa do eixo x temos:
Se o cabo termina numa resistência R, então esta gera um pulso refletido de modo que a
tensão e a corrente tem a forma:
(8)
(9)
No extremo do cabo temos x=l:
Substituindo a tensão (8) e correntes (9) na equação acima, obtemos:
(10)
A amplitude do pulso refletido é uma fração da amplitude do pulso incidente. Se R=0, o
∞ , o pulso refletido é igual ao pulso incidente.
pulso refletido será invertido, se R=∞
3. Montagem Experimental
•
4 cabos coaxiais com diversos comprimentos e com saída bnc;
•
osciloscópio de 100 MHz;
•
gerador de pulso (50 ns) com 4 saídas;
•
cabos coaxiais curtos para ligar as 4 saídas da fonte ao osciloscópio;
Prof. Márcia R. Gallas (FIS01059)
•
multímetro;
•
fios curtos (10 cm) com uma saída bnc e 2 jacarés na ponta;
•
uma ponte RLC para medir L e C dos cabos;
•
potenciômetro linear de 100 Ω;
•
paquímetro;
•
trena ou régua grande;
•
T´s com saída bnc.
4. Procedimento
Medir as dimensões geométricas dos cabos coaxiais completando a tabela. A seguir, medir a
capacitância C do cabo e calcular C′′ = C/l onde l é o comprimento do cabo. Usar o valor de
C′′ e a relação de C′′ teórica para calcular o εr do cabo. Calcular a indutância por unidade de
comprimento L′′. Finalmente, calcular a velocidade da onda e a impedância do cabo.
Cabo
(m)
2r1 (mm)
2r2 (mm)
C´ (pF)
εr
L′ (µ H m-1)
v (ms-1)
Z (Ω)
A seguir, meça num osciloscópio rápido o tempo de propagação da onda e determine o valor
da velocidade. Usando um potenciômetro variável, determine a impedância do cabo.
Prof. Márcia R. Gallas (FIS01059)
Cabo
(m)
tprop. (ns)
v (m s-1)
R = Z (Ω)
Questões
a. Descreva o pulso refletido quando o cabo coaxial está aberto num extremo.
b. Descreva o pulso refletido quando o cabo coaxial está em curto num extremo.
c. Descreva o pulso refletido quando R = Z.
RELATÓRIO:
Neste relatório siga o roteiro e proceda da seguinte maneira:
•
Verifique que I e V satisfazem a equação da onda, definindo a velocidade da onda
em termos de L´ e C´.
•
Deduza as expressões (5), (6) e (7).
•
Deduza a expressão (10).
•
Comente os resultados experimentais dispostos nas duas tabelas.
•
Responda às três questões no fim do roteiro.