Prova - Matemática

Matemática
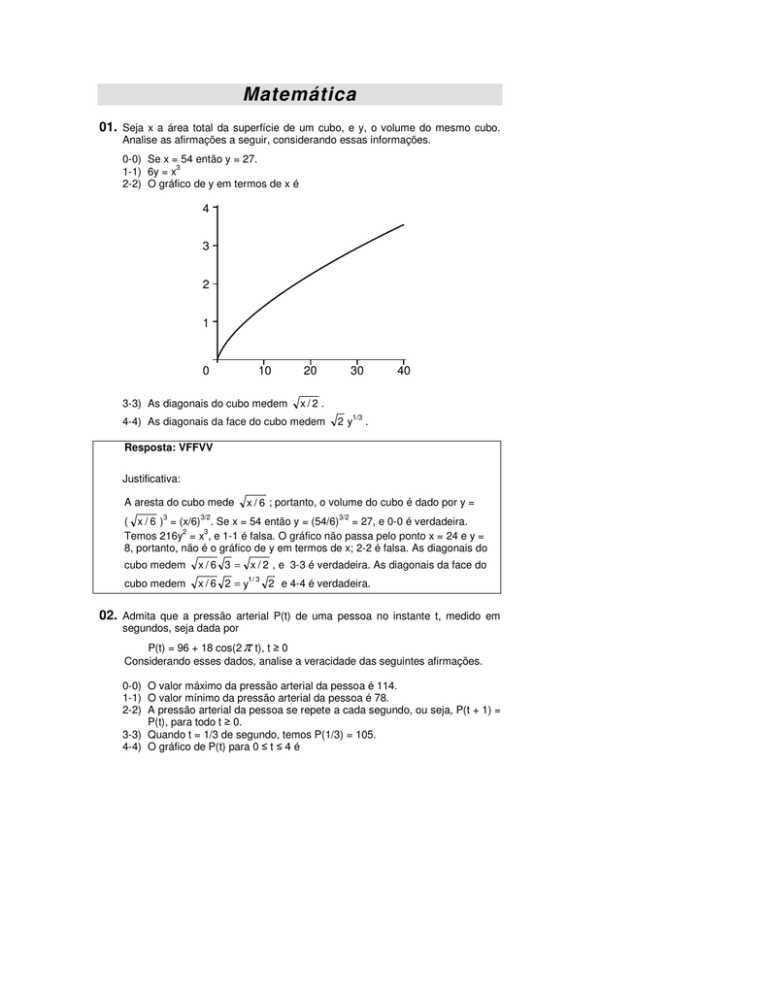
01. Seja x a área total da superfície de um cubo, e y, o volume do mesmo cubo.
Analise as afirmações a seguir, considerando essas informações.
0-0) Se x = 54 então y = 27.
3
1-1) 6y = x
2-2) O gráfico de y em termos de x é
4
3
2
1
0
10
3-3) As diagonais do cubo medem
20
30
40
x/2 .
4-4) As diagonais da face do cubo medem
1/3
2y
.
Resposta: VFFVV
Justificativa:
A aresta do cubo mede
3
x / 6 ; portanto, o volume do cubo é dado por y =
3/2
( x / 6 ) = (x/6) . Se x = 54 então y = (54/6)3/2 = 27, e 0-0 é verdadeira.
2
3
Temos 216y = x , e 1-1 é falsa. O gráfico não passa pelo ponto x = 24 e y =
8, portanto, não é o gráfico de y em termos de x; 2-2 é falsa. As diagonais do
cubo medem
x / 6 3 = x / 2 , e 3-3 é verdadeira. As diagonais da face do
cubo medem
x / 6 2 = y1 / 3 2 e 4-4 é verdadeira.
02. Admita que a pressão arterial P(t) de uma pessoa no instante t, medido em
segundos, seja dada por
P(t) = 96 + 18 cos(2 π t), t ≥ 0
Considerando esses dados, analise a veracidade das seguintes afirmações.
0-0) O valor máximo da pressão arterial da pessoa é 114.
1-1) O valor mínimo da pressão arterial da pessoa é 78.
2-2) A pressão arterial da pessoa se repete a cada segundo, ou seja, P(t + 1) =
P(t), para todo t ≥ 0.
3-3) Quando t = 1/3 de segundo, temos P(1/3) = 105.
4-4) O gráfico de P(t) para 0 ≤ t ≤ 4 é
110
105
100
95
90
85
80
0
1
2
3
4
Resposta: VVVFF
Justificativa:
O valor máximo ocorre quando cos(2 π t) = 1 ou 2 π t = 2k π e t = k, k inteiro
não negativo, e vale 96 + 18 = 114; logo, 0-0 é verdadeira. O valor mínimo
ocorre quando cos(2 π t) = -1 e vale 96 – 18 = 78; portanto, 1-1 é verdadeira.
P(t) é uma função periódica com período 2 π /(2 π ) = 1; daí, 2-2 é verdadeira.
Temos P(1/3) = 96 + 18cos(2 π /3) = 96 – 9 = 87, e 3-3 é falsa. Temos P(0) =
114, e o gráfico não é o de P(t), portanto, 4-4 é falsa.
03. Uma transportadora de volumes só aceita caixas na forma de paralelepípedos
retângulos quando a soma do perímetro da base e da altura é no máximo 2m.
Suponha que se pretenda transportar uma caixa, com maior volume possível,
no formato de um paralelepípedo com base quadrada, de lado x metros, e
altura h metros, como ilustrado na figura abaixo.
h
x
x
Para obtermos volume máximo, os valores de x e h devem satisfazer
4x + h = 2.
Analise as afirmações abaixo, considerando esses dados.
0-0)
1-1)
2-2)
3-3)
4-4)
3
2
O volume da caixa, em m , é dado por 2x (1 – 2x).
3
Quando o lado da base mede 1/3 de metro, o volume da caixa é (1/9)m .
A área total da caixa é -8x + 14x2, em m2.
A área total da caixa será máxima quando a altura for 6/7 de metro.
3
Quando a área total da caixa é máxima, seu volume é (24/343)m .
Resposta: VFFFV
Justificativa:
2
2
2
O volume da caixa é dado por x h = x (2 – 4x) = 2x (1 – 2x); logo, 0-0 é
3
verdadeira. Para x = (1/3)m, o volume será 2.1/9.1/3 = (2/27)m , logo 1-1 é falsa. A
2
2
2
2
área total da caixa é dada por 2x + 4xh = 2x + 4x(2 – 4x) = (8x – 14x )m ;
portanto 2-2 é falsa. A área total da caixa é máxima para x = -8/(2(-14)) = (2/7)m, e
3
o volume da caixa será 2.4/49.3/7 = (24/343)m ; portanto, 3-3 é falsa e 4-4
verdadeira.
04. Qual o coeficiente de x2 na expansão de
(1+ x) (1+ 2x) (1+ 3x) (1+ 4x) (1+ 5x)?
Resposta: 85
Justificativa:
O coeficiente de x2 é
(2 + 3 + 4 + 5) + 2(3 + 4 + 5)+3(4 + 5) + 4.5 = 14 + 24 + 27 + 20 = 85.
05. A ilustração a seguir é parte do gráfico de um polinômio p(x), de grau três e
com coeficientes reais. O gráfico passa pelos pontos (-3,0), (-1,0), (2,0) e (0,-1).
10
8
6
4
2
-4
-3
-2
-1
1
2
3
4
-2
Indique o valor de p(6).
Resposta: 42
Justificativa:
Justificativa: p(x) é divisível por x – 2, x + 1 e x + 3, logo é da forma p(x) = a(x
– 2)(x + 1)(x + 3), com a real. De p(0) = -1, obtemos -1 = a(-2).1.3 e a = 1/6.
Assim, p(x) = (x – 2)(x + 1)(x + 3)/6 e p(6) = 42.
06. Uma calha tem a forma de um prisma reto de base triangular. A altura do
prisma é 1m, e sua base é um triângulo isósceles com lados congruentes,
medindo 0,4m e formando entre si um ângulo α .
α
Fazendo a escolha apropriada, qual o maior volume, em litros, que a calha
pode ter?
Resposta: 80
Justificativa:
A área da base da calha é 0,42sen α /2 = 0,08sen α , e o volume da calha é
3
0,08sen α .1 = 0,08 sen α (em m ). O volume da calha será máximo quando
o
α = 90 , e o volume máximo será 0,08 m3 = 80 dm3 = 80 litros.
07. O preço do produto X é 20% menor que o do produto Y, e este, por sua vez,
tem preço 20% maior que o do produto Z. Se os preços dos três produtos
somam R$ 237,00, quanto custa, em reais, o produto Z?
Resposta: 75
Justificativa:
Seja z o preço do produto Z. Então, Y custa 1,2z e X custa 0,8.1,2z = 0,96z.
Temos z + 1,2z + 0,96z = 237 e segue que z = 237/3.16 = 75.
08. Admita que o lucro mensal de uma companhia de telefone celular que tem x
milhares de assinantes seja de (24x – 400) milhares de reais. No momento, o
lucro da companhia é de 320 mil reais. Quantas novas dezenas de assinantes
são necessárias para que o lucro da companhia passe de 320 mil reais para
332 mil reais?
Resposta: 50
Justificativa:
O lucro é de 320 mil reais, quando o número de assinantes é (320 + 400)/24 =
30 mil e de 332 mil, quando o número de assinantes é (332 + 400)/24 = 30,5
mil. Portanto, são necessários mais 0,5 mil = 500 assinantes.
09. Calcule a distância d entre os pontos de interseção das circunferências com
equações.
2
2
2
2
x + y – 2x – 2y +1 = 0 e x + y – 4x – 2y + 4 = 0.
2
Indique 4d .
Resposta: 12
Justificativa:
Para calcularmos os pontos de interseção, subtraímos as igualdades, e
2
obtemos 2x – 3 = 0 e x = 3/2; substituindo x = 3/2 na primeira equação obtemos y
– 2y + ¼ = 0 e y = (2 ±
3 )/2. A distância entre os pontos de interseção é d = (2
+
2
3 . Portanto, 4d = 12.
3 )/2 - (2 -
3 )/2 =
10. Um paciente toma diariamente 0,06mg de certa droga. Suponha que o
organismo do paciente elimina, diariamente, 15% da quantidade desta droga
presente no organismo. Assim, no momento, após ser administrada a droga,
permanecem no organismo do paciente, além desta dose, o remanescente das
doses dos dias anteriores. Na tabela abaixo, temos a quantidade da droga
presente no organismo do paciente, em mg, nos dias depois do início do
tratamento, após ser administrada a dose diária:
1º dia
2º dia
3º dia
0,06
0,06 + 0,85.0,06
2
0,06 + 0,85.0,06 + 0,85 .0,06
etc.
Assim, no n-ésimo dia permanece no organismo do paciente um total de (0,06
n-1
+ 0,85.0,06 + ... + 0,85 . 0,06) miligramas da droga.
Determine a quantidade q da droga, em mg, presente no organismo do
paciente, após um ano de tratamento e assinale 100q. Dado: use a
365
aproximação 0,85 ≈ 0.
Resposta: 40
Justificativa:
A quantidade da droga presente no organismo do paciente é q = 0,06 +
364
0,85.0,06 + ... + 0,85
365
.0,06 = 0,06(1 - 0,85
)/(1 – 0,85)
≈ 0,4.
11. O número de quatro dígitos 1391 tem a propriedade seguinte: o número
formado tomando quaisquer dois de seus dígitos consecutivos é divisível por
13. Existe um número com 100 dígitos, com o primeiro dígito (à esquerda) igual
a 3, tendo a mesma propriedade. Indique o número formado pelos dois últimos
dígitos (à direita) deste número.
Resposta 13
Justificativa:
Justificativa: Os múltiplos de 13 com dois dígitos são 13, 26, 39, 52, 65, 78,
91. Portanto, os dois primeiros dígitos do número com 100 dígitos são 3 e 9,
uma vez que 39 é o único múltiplo de 13 entre 30 e 40; analogamente, o
dígito seguinte é 1, uma vez que 91 é o único múltiplo de 13 entre 90 e 100.
Portanto, o número começa com os dígitos 3, 9 e 1. Repetindo o argumento,
concluímos que o número de 100 dígitos contém 33 repetições de 391 e o
número formado pelos dois últimos dígitos é 13.
12. Em uma gaveta, estão quatro pares de meias, cada par de uma cor diferente.
Escolhendo aleatoriamente duas das meias da gaveta, qual a probabilidade
percentual p% de elas serem da mesma cor? Indique o inteiro mais próximo de
p.
Resposta: 14
Justificativa:
O número de maneiras de se escolher duas meias da gaveta é 8.7 / 2 = 28 ,
e o número de maneiras de se obter duas meias da mesma cor é 4; portanto,
a probabilidade percentual de se obter um par de meias da mesma cor é
100.4/28 = 14,28%.
13. João e Maria possuem, juntos, R$ 510,00. Se, simultaneamente, João
presenteia Maria com 1/8 do que ele possui, e Maria presenteia João com 1/6
do que ela possui, então, os dois ficarão com quantias iguais. Em quantos reais
a quantia que Maria possuía inicialmente excede a que João possuía?
Resposta: 30
Justificativa:
Seja j a quantia, em reais, que João possuía inicialmente; assim, Maria
possuía 510 – j. Se João presenteia Maria com j/8 reais, lhe restaram 7j/8, e
se Maria presenteia João com (510 - j)/ 6, lhe restaram 5(510 – j)/6.Temos
que 7j/8 + (510 - j)/6 = 5(510 – j)/6 + j/8. Portanto, simplificando esta
igualdade, obtemos 3j/4 = 2(510 – j)/3, que equivale a 9j = 4080 – 8j , e daí j
= 4080/17 = 240 reais. A quantia que Maria possuía inicialmente era de 510 –
240 = 270, e a diferença entre as quantias que os dois possuíam era de 270 –
240 = 30 reais.
14. Indique a solução da equação 2x - 5 + 22x - 13 = 5/2.
Resposta: 06
Justificativa:
x-4
A equação equivale a 2
2x - 12
+2
x-6
4± 16 + 20 )/2 = (-4 ± 6)/2 e 2
x-6 2
x-6
= 5, ou a (2 ) +4.2
= 1, logo x = 6.
x-6
- 5 = 0. Daí 2
= (-
15. Sabendo que 1+ i é uma das raízes da equação x3 – 2x + a = 0, com a real,
indique o valor de a.
Resposta: 04
Justificativa:
3
Substituindo 1 + i na equação obtemos (1+ i) – 2(1+ i) + a = 0, que se reduz a
1 + 3i – 3 – i - 2 – 2i + a = 0, e a = 4
16. Na figura abaixo, quatro das cinco circunferências possuem o mesmo raio. Três
destas são tangentes à circunferência de maior raio e têm centros em vértices
de um triângulo eqüilátero. A quarta circunferência de raio menor é tangente às
outras três. Se a e b representam as áreas das regiões de cor cinza indicadas
na figura, assinale 100a/b.
a
b
Resposta: 60
Justificativa:
Temos a = πr2 e b = (π (3r)2 – 4π r2)/3 = 5πr2/3. Portanto 100a/b = 100.3/5 =
60.