II Edição do Jornal Matemática para Todos

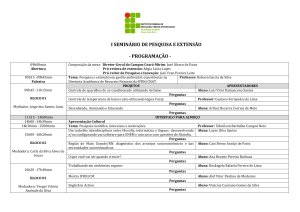
Edição II
Jornal
15 de fevereiro de 2016
Um informativo bimestral feito por professores e estudantes
Noticiário
MATEMÁTICA:
EDUCAÇÃO BÁSICA &
FORMAÇÃO DE
PROFESSORES DE
MATEMÁTICA NO BRASIL
A Conjectura de Goldbach
.
Prof. Ms. Rafael Pereira de Melo
O que faz o estudo dos números primos tão
interessante que levou Gauss a chamá-la de ‘rainha
da matemática’?
A história mostrou muitas teorias acerca dos
números primos, muitos delas, de fundamental
importância para o desenvolvimento da Teoria dos
Números. Outras teorias que foram apresentadas
não puderam ser demonstradas, ou seja, não se sabe
se são verdadeiras ou não. Para essas teorias
chamamos de conjecturas. Em outras palavras,
uma conjectura matemática é uma proposição que
acreditamos ser verdadeira, porém, ainda não
conseguimos prová-la.
Em 7 de junho de 1742 o matemático Christian
Goldbach escreveu, em carta ao também
matemático Leonhard Euler, que todo número
inteiro par maior do que 2 é igual a soma de dois
n ú m e ro s p r i m o s . V á r i o s m a t e m á t i c o s j á
verificaram-a para milhões de números pares. Mas
isso não é suficiente para que a conjectura vire um
teorema, ou seja, é preciso que se encontre uma
prova assegurando que qualquer número par pode
ser escrito como soma de dois primos.
Goldbach propôs ainda uma versão fraca de sua
conjectura, em que afirma que todo número ímpar
maior do que 7 pode ser expresso como soma de
três primos ímpares. O adjetivo fraca é devido ao
Licenciatura em Matemática
GOLDBACH
E SUA CONJECTURA POR
RAFAEL P. DE MELO
RESOLVENDO UM
PROBLEMA
WHARTON M. DE LIMA
SUGESTÃO DE LEITURA
JÁFIA GILEANE
fato desta versão se tratar de um caso particular da
versão anterior, pois todo inteiro ímpar maior do
que 7 é a soma de 3 com um inteiro par maior do
que 4.
A conjectura ainda não foi demostrada, mas se têm
conseguido avanços importantes, principalmente na
sua versão fraca. Em 1923, G. H. Hardy e J. E.
Littlewood mostraram que, assumindo a Hipótese
Riemann, a versão fraca é verdadeira para inteiros
ímpares suficientemente grandes. Em 1937, I. M.
Vinogradov eliminou a dependência da Hipótese de
Riemann. Com o auxílio de computadores alguns
matemáticos tentam verificar a veracidade da
conjectura para todos os números até 10²³. Com a
tecnologia atual a previsão para terminar a
verificação “era” de 20 anos. Porém, o matemático
peruano Harald A. Helfgott conseguiu demonstrar a
versão fraca. O responsável pela façanha tem 35
anos e vive em Paris, onde trabalha para o Centro
Nacional para a Pesquisa Científica. Helfgott
publicou uma solução parcial em 2012 e neste ano
mais dois artigos que demonstrou, definitivamente,
a Conjectura fraca de Goldbach.
No entanto, essa pesquisa dificilmente contribuirá
para a comprovação de um dos problemas mais
antigos não resolvidos da matemática, considerado
por muitos o problema mais difícil da história dessa
ciência. De acordo com o próprio Helfgott, a
Conjetura de Goldbach “pode não ser resolvida nas
nossas vidas”.
IFRN – CNAT
1
Edição II
Noticiário
Em entrevista à Folha de SP, o
matemático Marcelo Viana,
novo presidente do Impa, fala
sobre o ensino da matemática
no Brasil. Ele abordou os
problemas da educação básica
no país e as preparações para o
Biênio da Matemática no país,
que acontece em 2017, ano em
que sediaremos a Olimpíada
Internacional de Matemática, e
em 2018, ano em que o Rio de
Janeiro sediará o Congresso
Internacional dos Matemáticos.
Segundo Viana, vivemos hoje
um paradoxo: apesar de o Impa
ser uma instituição de pesquisa
de ponta e de termos um
brasileiro como ganhador da
Medalha Fields, o Brasil patina
na educação básica e a
formação de professores nas
licenciaturas é “catastrófica”. “As
crianças nascem gostando de
matemática. Os professores é
que se encarregam de acabar
com isso”, diz Viana. Leia a
íntegra da entrevista no link:
folha.com/no1734373
Jornal Matemática Para Todos
15 de fevereiro de 2016
Explorando e resolvendo um problema
Prof. Ms. Wharton Martins Lima
Ao lecionar a disciplina A Arte de Resolver Problemas, para
alunos do curso de Licenciatura em Matemática (IFRN–CNAT),
tenho procurado encontrar situações-problema que possibilitem
aos alunos uma estratégia de redescoberta que os auxiliem na
resolução, no sentido de encontrar novos caminhos e, se possível,
generalizar as soluções. Segundo LESTER (1982), são problemas
de processo que exigem várias operações e estratégias adequadas
que levam à construção da solução. Vejamos uma adaptação de
um problema proposto por ZIMMERMANN (1985).
Problema: Em uma superfície retangular (Figura 1) existem 10
pontos, sendo que não há 3 pontos colineares e nenhum deles
sobre algum vértice ou aresta do retângulo. Quantos triângulos
podemos formar sem que os lados dos triângulos se cruzem?
EXPLORAÇÃO
Lados
Pontos Triângulos
4
1
4
(b)
4
2
6
(c)
4
3
8
(a)
* * *
A Academia Brasileira de
Ciências (ABC) sediou, no final
de 2015, simpósio com o tema
“Desafios da Educação TécnicoCientífica no Ensino Médio”. O
evento contou com especialistas
de diversas áreas com trabalhos
ligados à educação e buscou
discutir problemas como o
ensino deficiente nas escolas e a
má formação de professores.
Daniel Ximenes (Capes)
mostrou dados indicativos de
que 80% dos ingressantes em
cursos de licenciatura em
matemática não concluem o
curso. Leia + bit.ly/mat-abc
Licenciatura em Matemática
IFRN – CNAT
2
Edição II
Jornal Matemática Para Todos
15 de fevereiro de 2016
Note que o número de triângulos em cada caso é
dado por: (a) 4 = 2x1 + 2,; (b) 6 = 2x2 + 2; e (c) 8 =
2x3 + 2. De onde podemos deduzir que com 10
pontos é possível formar 2x10 + 2 = 22 triângulos.
De forma geral, com n pontos é possível formar 2n +
2 triângulos.
Uma solução baseada nos ângulos internos
a) Vamos chamar de S1 a soma das medidas dos
ângulos rasos em torno de cada ponto. No caso de
10 pontos, temos S1 = 10x360º = 3600º. No caso
geral, ou seja, de n pontos, temos S1 = 360ºn.
b) Chamaremos de S2 a soma dos quatro ângulos
retos. Em quaisquer dos casos, temos que S2 =
4x90º = 360º.
Mas dado que a soma dos ângulos internos de um
triângulo é igual a 180 graus, obtemos:
10 pts: (S1+S2)÷180º = 3960º ÷ 180º = 22 triângulos
n pts: (360ºn + 360º) ÷ 180º = 2n + 2 triângulos
Desafio
Se ao invés de retangular a figura fosse triangular,
qual seria a expressão para o número de triângulos
no caso de n pontos? E se fosse pentagonal ou
hexagonal?
⚠ Mande suas soluções pra gente, no e-mail:
[email protected]
⚠
Referências bibliográficas
Charles, R. and Lester, F. Teaching Problem
solving: What, why and how. Palo Alto, CA: Dale
Seymour Publication, 1982.
Zimmermann, B. Find Problem Solving to Finding
in Mathematics Instructor. Mathematics Education
Research in Finland, 1985.
Christian Goldbach (1690 – 1764)
Quem fez história
Christian Goldbach, filho de um pastor
russo, estudou legislação e matemática.
Viajou por toda a Europa e conheceu
pessoalmente muitos matemáticos
famosos, incluindo Leibniz, Euler e Nicolau I
Bernoulli. Muito pouco se sabe sobre sua
juventude e sua vida antes de seu ingresso,
em 1725, como professor de matemática e
historiador, na Academia de Ciências de
São Petersburgo. Foi lá, três anos mais
tarde, que tornou-se tutor do czar Pedro II,
Imperador da Rússia. Sua carreira como
matemático é conhecida pelas inúmeras
contribuições à Teoria dos Números, sendo
a mais conhecida delas a conjectura que
leva seu nome, à teoria das curvas, às series
infinitas e à integração de equações
diferenciais. Boa parte dessas contribuições
foram registradas através de suas inúmeras
cartas a matemáticos de várias partes do
mundo, sendo o matemático suíço Euler
àquele com quem mais se comunicou. Era
a Euler que Goldbach solicitava que
t e s t a s s e s u a s t e o r i a s e p ro b l e m a s
matemáticos, em especial sobre sua
conjectura a cerca da decomposição de
números como soma de números primos.
Essa correspondência com Euler marca
Goldbach como um dos poucos homens
d e s u a é p o c a q u e e n t e n d e ra m a s
implicações da nova abordagem de Fermat
para a Teoria dos Números.
Fonte:
MacTutor History
Prof. Francisco Medeiros
Licenciatura em Matemática
IFRN – CNAT
3
Edição II
Jornal Matemática Para Todos
Fique esperto!
Sugestão de leitura
Podemos dizer que nossa seção de problemas da
edição anterior foi um sucesso. De fato, vários
leitores nos enviaram a solução para o problema da
“estrela camaleoa” e o aluno Gabriel Navarro
1º Ano de Mecânica (IFRN/CNAT), enviou a
seguinte solução do problema “João & Maria”:
O Homem que
Calculava. Resenha:
Durante uma viagem à
Bagdá, no meio da
estrada, Hank, o
narrador da história,
avista um homem
sentado embaixo de
uma
árvore,
exclamando números
absurdamente altos. Com curiosidade, foi lhe
perguntar o que significava todos aqueles
números e acabaram tornando-se amigos.
Seu nome era Beremiz Samir, um calculista
brilhante que desenvolveu sua habilidade
com o auxílio da natureza, contando ovelhas.
De forma simples e fantástica, o calculista
soluciona enigmas matemáticos
aparentemente insolúveis, explorando suas
mais diversas áreas e utilizando a lógica
como ferramenta para a resolução dos
problemas. No livro, a matemática é
apresentada de forma divertida e variada no
cotidiano das pessoas, trazendo um pouco
de sua história e grandes nomes envolvidos
nela.
Para a Pergunta 1: Nunca se encontrarão, pois o
limite de 27/3^n quando n tende a +∞ é igual a 0.
Comentário do editor: Teríamos aqui um paradoxo?
Para a Pergunta 2: Após a 5ª etapa, pois no começo
dela estarão à ~110m um do outro, enquanto na
etapa anterior estarão a ~ 300m.
Para a Pergunta 4: Para complicar a vida alheia.
Cruz vermelha
Você sabia que A Cruz Vermelha Internacional e seu
logo foram criados pelo suíço e prêmio Nobel da
Paz de 1901 Jean Hanri Dunant em 1863? E que ele
usou uma inversão da bandeira suíça para criar o
logo, ou seja, cruz em vermelho no fundo branco? É
bem provável que você já tenha lido sobre isso por
aí! Mas será que você é capaz de encontrar formas
de dividir a “cruz vermelha” em quatros regiões de
mesma área? Por exemplo, temos abaixo dois
modos diferentes.
⚠
Por Jáfia Gileane, estudante da Licenciatura
em Matemática – IFRN / CNAT
Mande suas soluções pra gente, no e-mail:
[email protected]
15 de fevereiro de 2016
⚠
O Jornal Matemática para Todos é um Projeto
de Extensão, aprovado junto à PROEX–IFRN
pelo Edital de Fluxo Contínuo 01/2015,
idealizado e produzido por professores e
estudantes do Curso Superior de Licenciatura
em Matemática do IFRN, Campus Natal
Central.
Quem fez
Prof. Dr. Francisco Medeiros (editor e coordenador)
[email protected]
Prof. Ms. Rafael Melo (colaborador)
[email protected]
Prof. Ms. Wharton M. de Lima (colaborador)
Jáfia Gileane (colaboradora)
Licenciatura em Matemática
[email protected]
[email protected]
IFRN – CNAT
4