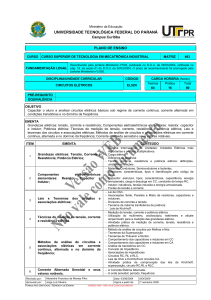
Números Complexos
4 ?
Definição:
Unidade imaginária:
Professor: Neury Boaretto
j 1
ou
j 2 1
Desta forma:
Material disponibilizado pelo autor do livro em: www.eletronica24h.com.br
4 ( 1).4
Curso Online: http://www.eletronica24h.com.br/Curso%20CA/index.htm
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Formas de Representação de um Numero Complexo
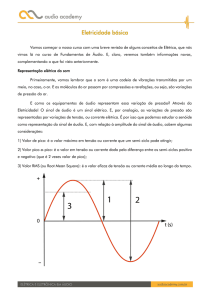
Deduções:
•Forma Cartesiana (Retangular)
•Forma Polar
•Forma Trigonométrica
j 3 j 2 . j ( 1). j j
j 4 j 2 . j 2 ( 1).( 1) 1
5
2
1. 4 j 2
Forma Cartesiana
2
j j . j . j ( 1).( 1). j j
a e b são números reais
Z=a+jb
j 6 j 2 . j 2 . j 2 ( 1).( 1).( 1) 1
j é a unidade imaginária
Analise de Circuitos em Corrente
Alternada - Ed. Erica
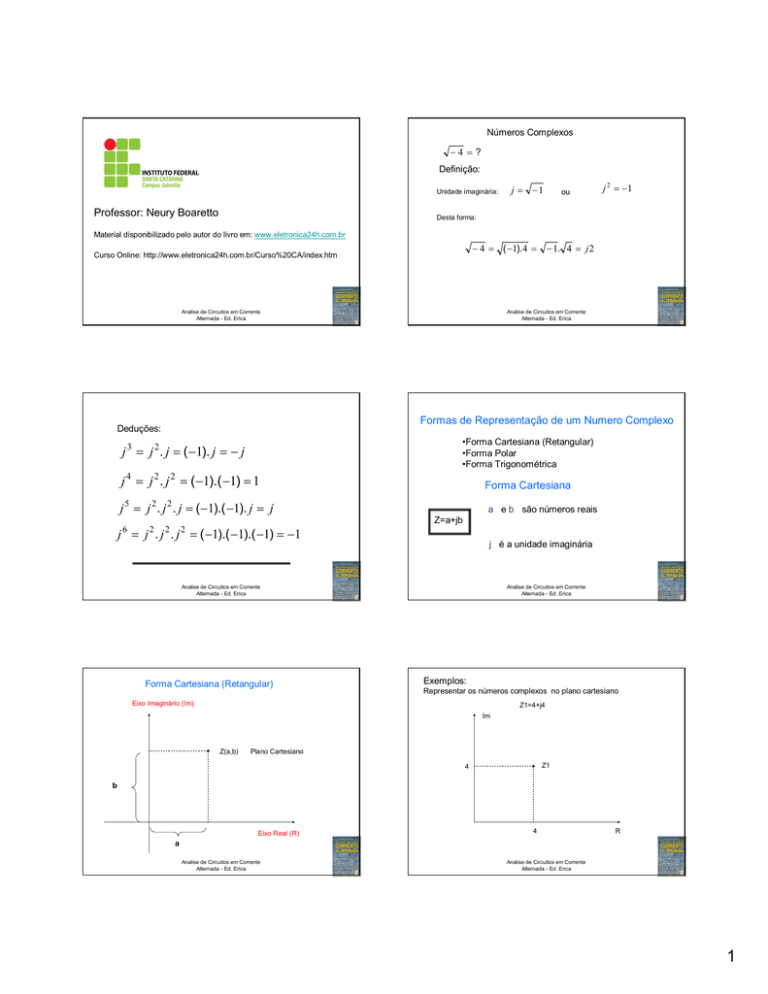
Forma Cartesiana (Retangular)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Exemplos:
Representar os números complexos no plano cartesiano
Eixo Imaginário (Im)
Z1=4+j4
Im
Z(a,b)
Plano Cartesiano
Z1
4
b
Eixo Real (R)
4
R
a
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
1
Z3=j3 (não tem parte real)
Z2=7 (não tem parte imaginária)
Im
Im
Z3
3
Z2
R
7
R
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Z5=3+j3
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Forma Polar
Z4=-3+j2
Im
Z4
Im
MÓDULO
Z=a +jb forma cartesiana
Z5
3
b
P
FASE
2
Z
1
-3
1
-1
-2
2
3
R
-1
o
Segmento de reta
OP Z
Representa o MODULO
Do numero complexo z
-2
a
R
O ângulo representa o
ARGUMENTO ou ÂNGULO DE
FASE de z
-3
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Transformação da Forma Cartesiana para Polar
Forma Polar
Na forma polar um numero complexo é representado por:
Z a 2 b2
Dado: z=a+jb
Im
Determinar: Z e
z= Z
Z é o módulo
e
é a fase do numero complexo
tg
b
a
arctg
Numero complexo é representado por letra minúscula, z
b
b
Z
a
Z= Z
Forma alternativa
Analise de Circuitos em Corrente
Alternada - Ed. Erica
R
a
E o seu módulo por letra maiúscula, Z
z= Z
Analise de Circuitos em Corrente
Alternada - Ed. Erica
2
Exemplos:
Transformar os números para a forma polar
Z2=7 (não tem parte imaginária)
Z1=4+j4
Z2=7
Im
Z1
4 2 42 4 2
Im
2=00
z1
4
1 arctg
Z1
4
4
45
0
1
2
R
4
z1 = 4 2
Z2
Analise de Circuitos em Corrente
Alternada - Ed. Erica
7
00
z2 = 7
z2
450
R
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Z4=-3+j2
z3=j3 (não tem parte real)
Im
Z3=3
3=900
Im
z3
Z 4 ( 3) 2 2 2 13 3,6
z4
3
z3 = 3
Z3
900
' arctg
2
Z4
4
’
3
4=180-34=1460
R
-3
Ou..........
2
340
3
R
z3 = 3
2700
z4 = 3,6
Analise de Circuitos em Corrente
Alternada - Ed. Erica
1460
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Z6=-4-j3
Z5=-5
Im
Im
Z5=5
6
5=1800
Z 6 (4 )2 ( 3) 2 5
' arctg
-4
3
37 0
4
5
’
z5
Z5
R
Z6
-3
R
z5 = 5
z6
1800
Analise de Circuitos em Corrente
Alternada - Ed. Erica
6=180+37=2170
z6 = 5
2170
Analise de Circuitos em Corrente
Alternada - Ed. Erica
3
Z7=-j4
Z8=4-j3
Z7=4
Im
Im
Z 8 4 2 ( 3) 2 5
7=2700
7
' arctg
8
3
370
4
4
R
z7
z7 = 4
-4
R
’
2700
-3
Z8
z8
z8 = 5
Ou.....
z7 = 4
8=360-37=3230
90 0
ou...............
z8 = 5
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Operações com Números Complexos
SOMA e SUBTRAÇÃO
Na soma e na subtração é usada a forma cartesiana
3230
37 0
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Operações com Números Complexos
MULTIPLICAÇÃO E DIVISÃO
Na multiplicação e divisão é usada a forma polar
z1=4+j4=5,65 450
Z3=-j4=4 -900
z1=10+j10 z2=5+j4
z2=5+j8,66=10 600
Z4= -5+j8,66= 10 1200
z3=z1+z2=(10+j10) + (5+j4)= (10+5)+j(10+4)=15+j14
z4=z1-z2= (10+j10) - (5+j4)= (10-5)+j(10-4)=5+j6
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Exercícios Propostos
Analise de Circuitos em Corrente
Alternada - Ed. Erica
MANIPULAÇÃO DE NÚMEROS COMPLEXOS
EM CALCULADORAS ELETRÔNICAS
Dados os complexo:
z1=4+j4=5,65 450
Z3=-j4=4 -900
z2=5+j8,66=10 600
Z4= -5+j8,66= 10 1200
Obter:
a) Representação no plano cartesiano de z1,z2,z3 e z4
b) z2.z4
z2.z3
c) z2/z4
z2/z3
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
4
MANIPULAÇÃO DE NÚMEROS COMPLEXOS
EM CALCULADORAS ELETRÔNICAS
MANIPULAÇÃO DE NÚMEROS COMPLEXOS
EM CALCULADORAS ELETRÔNICAS
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
MANIPULAÇÃO DE NÚMEROS COMPLEXOS
EM CALCULADORAS ELETRÔNICAS
MANIPULAÇÃO DE NÚMEROS COMPLEXOS
EM CALCULADORAS ELETRÔNICAS
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
MANIPULAÇÃO DE NÚMEROS COMPLEXOS
EM CALCULADORAS ELETRÔNICAS
Tensão Alternada
Tensão Continua: Tensão que tem sempre a mesma polaridade
Símbolo
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Uxt
Analise de Circuitos em Corrente
Alternada - Ed. Erica
5
Tensão Senoidal
Tensão Alternada
É uma tensão que varia com o tempo de acordo com uma lei senoidal
É uma tensão cujo valor e polaridade se modificam ao longo do tempo.
Conforme o comportamento da tensão então temos os diferentes tipos de tensão:
Senoidal, quadrada, triangular, pulsante, etc
T=Período
Representação Gráfica e Expressão Matematica
v(t) = VP.sen(w.t +θ0)
ω é a freqüência angular
VPP
VP
VP é o valor de pico
VPP é valor de pico a pico
θ0 é o ângulo de fase inicial
θ = ω.t +θ0
VP= valor de pico=12V
VPP=valor de pico a pico=24V
No exemplo
v(t) = 10.sen(1000.π.t ) (V)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Representação Gráfica e Expressão Matemática
Período (T) e Frequência (f)
v(θ) = VP.sen θ
Período (T) é o tempo necessário para o fenômeno voltar a se repetir
(completar um ciclo)
T segundo(s)
Freqüência (f) é o numero de ciclos completados por segundo
θ=w.t=ângulo descrito
f Hz
ou ciclo / segundo
1
T
T
f
Analise de Circuitos em Corrente
Alternada - Ed. Erica
1
f
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Movimento Circular Uniforme
Frequência Angular (ω)
A=amplitude do segmento
Representa a variação angular em função do tempo
rd / s ou
graus / s
θ = ω.t
Se
2.π = ω.T
θ=2.π, o tempo será t= T
2.
T
ou
2. . f
A projeção do segmento no eixo vertical representa uma grandeza
senoidal de amplitude A e fase inicial θ0
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
6
Movimento Circular Uniforme
Movimento Circular Uniforme
Neste caso a grandeza senoidal tem ângulo de fase inicial 0 e portanto
a expressão que representa a grandeza é: A.sen(w.t)
Neste caso o ângulo de fase inicial é -45 graus e a expressão em função do tempo
que representará a grandeza em questão será: A.sen(w.t-45)
Em todos os casos a grandeza em questão pode ser tensão, onde A será
O valor de pico (Vp) e w a frequencia angular a qual estará relacionada com
A frequencia por w=2.π.f
Analise de Circuitos em Corrente
Alternada - Ed. Erica
V(V)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de um sinal senoidal
Determinando um valor de tensão
Expressão em função do tempo:
V(t)=5.sen(8.π.t) (V)
V(t)=5.sen(8.π.t) (V)
Qual o valor da tensão para t=0,6s? V(0,6s)=5.sen(8. π.0,6) =2,94V
5
0
0,250
0,500
0,125
0,375
t(s)
5V
2,94
-5
0,125
0,250
0,375
0,500
0,625
0,850
0,975
1,000
Tensão de pico: VP =5V
0,6
Tensão de pico a pico: VPP=10V
f
Período: T=0,25s
Analise do sinal
1
4 Hz
0,25
-5V
Frequência Angular: w=2.π.4=8.π rd/s
Ângulo de fase inicial: θ0=0
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Ângulo de Fase Inicial
Ângulo de Fase Inicial
Se para t=0 a tensão é diferente de zero, dizemos que o sinal tem uma
fase inicial.
Sinal atrasado
v(t) = VP.sen(w.t +θ0)
Sinal adiantado
Θ0 < 0
Para o exemplo: v(t)=VP.sen(w.t-900) (V)
v(V)
VP
Θ0 > 0
v(V)
VP
Para o exemplo: v(t)=VP.sen(w.t+900) (V)
θ0
w.t(rd)
θ0
w.t(rd/s)
-VP
-VP
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
7
Exemplos
Para os sinais pedem-se determinar: a) Freqüência angular b) freqüência
c) Periodo d) Ângulo de fase inicial e) Representar graficamente
f) Indicar o valor da tensão para t=0
e)
1) v1(t)=10.sen(20.000. π.t + π/3) (V)
a) w=20.000. π rd/s
600
b)
20.000 .
10.000 Hz 10 KHz
2.
2.
f
c) T
d)
1
0,0001s 0,1ms 100 s
10 .000
Θ0= π/3=600
f) No instante t=0 v1(0)=10.sen(w.0+600)=8,66V
Analise de Circuitos em Corrente
Alternada - Ed. Erica
V2=15.sen(8.000. π.t – 300) (V)
a) w=8.000. π rd/s
8 .000 .
b)
f
4. 000 Hz 4 KHz
2 .
2 .
c) T
d)
e)
1
0,00025 s 0,25 ms 250 s
4.000
Θ0=-300
f) No instante t=0 v2(0)=15.sen(w.0-300)=-7,5V
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Defasagem
A diferença de fase (Δθ) entre dois sinais de mesma freqüência
é chamada de defasagem, sendo medida tomando-se um dos sinais
como referencia
Ex: Qual a defasagem entre os sinais a seguir
v1(t)=10sen(w.t+π/2) (V)
v2(t)=5.sen(w.t) (V)
Δθ=θ1 – θ 2=90-0=90
300
-7,5V
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
v1(t)=10sen(w.t+900) (V)
v2(t)=5.sen(w.t+900) (V)
Δθ=90 – 90=0
Δθ
v1 está 900 adiantado em relação a v2
Os sinais estão em QUADRATURA
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Sinais estão em FASE
Analise de Circuitos em Corrente
Alternada - Ed. Erica
8
Representação Através do Diagrama Fasorial
v1(t)=10sen(w.t) (V)
v2(t)=5.sen(w.t+180)(V)
Δθ=180 – 0=180
É uma outra forma de representar uma tensão senoidal.
Vetor girante
Cada vetor (neste caso chamado de fasor), representa a tensão em um
determinado instante.
Observar que a tensão instantânea é a projeção no eixo vertical do vetor girante
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Representar os sinais no Diagrama fasorial (DF)
Diagrama Fasorial (DF)
Tensão senoidal representada no DF
V1 (t)=10.sen(w.t + 900)
10.sen(θ)
O fasor de amplitude 10V gira no sentido anti horario com
frequencia angula w
Analise de Circuitos em Corrente
Alternada - Ed. Erica
V2 (t)=10.sen(w.t - 90o)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Defasagem entre as duas tensões
V1 está adiantada em relação a V2
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
9
Representação na Forma Complexa
Exercício Proposto
Numero Complexo tem:
Modulo
e
fase
1) Desenhar o Diagrama Fasorial dos sinais:
Tensão Senoidal tem:
Modulo
e
fase
v1(t)=10.sen(w.t+600) (V)
v2(t)=15.sen(w.t-300) (V)
Portanto..........................
2) Qual defasagem entre as tensões?
Forma Trigonometrica: v(t)=VP.sen(w.t+θ 0)
Forma Complexa:
Analise de Circuitos em Corrente
Alternada - Ed. Erica
v=VP
θ0
VP.cos θ0 + j V P.sen θ 0
a
b
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Dadas as tensões
Resumo: Formas de representar uma tensão senoidal
v1(t)=10sen(w.t+π/2) (V)
v2(t)=5.sen(w.t) (V)
Expressão Trigonométrica
Pede-se: a) v3= v1+V2
v(t)=12.sen(w.t+600) (V)
b) Representar V3 no diagrama fasorial
c) Dar a expressão de V3(t) d) Representar V3 na forma polar e cartesiana
Diagrama Fasorial
Numero Complexo
v 6 j10,39 ( V )
Forma de Onda
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Circuitos Resistivos em CA
Em um circuito puramente resistivo (só com resistências) alimentado com uma
tensão alternada (CA) a tensão e a corrente estão em fase, sendo a relação entre
elas dada pela lei de ohm, isto é :
Como tensão e corrente estão em fase, concluímos que:
V(t) =Vp.sen(ω.t+θ0)
i( t )
v( t ) VP .sen( .t 0 )
IP .sen( .t 0 )
R
R
Analise de Circuitos em Corrente
Alternada - Ed. Erica
IP
VP
R
Uma resistência pode ser representada por um numero complexo
Com parte imaginaria nula
Analise de Circuitos em Corrente
Alternada - Ed. Erica
10
Valor Eficaz (VRMS)
A Tensão Alternada é senoidal
Dado uma tensão alternada (qualquer) v(t) define-se valor eficaz
T
Definição matemática:
VRMS
1
. v 2 (t)dt
T 0
Qual deve ser o valor da tensão continua para aquecer R igualmente ?
Significado Físico: O valor eficaz de uma tensão alternada
senoidal é igual ao valor da tensão continua que produz mesmo
aquecimento
V
VP
2
VEficaz VRMS
RMS= Root Mean Square = valor quadrático médio
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Como Calcular a Potencia dissipada em CC ?
E no caso de uma tensão senoidal?
Vp
P V.I
2
P
Qual a relação entre a tensão da bateria e a tensão de pico da senoide
para que o aquecimento seja o mesmo nos dois casos?
V
R
P VRMS .IRMS
P
P R.I2
2
P R.IRMS
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Potencia
Qual o valor da tensão continua que produz mesmo aquecimento em um resistor
de 50 ohms ligado a uma tensão senoidal de 310V de pico?
VRMS 2
R
em Circuito Resistivo em CA
A potencia em CA é obtida pelo produto do valor instantâneo da tensão pela corrente
instantânea:p(t)=v(t).i(t)
p(t)=v(t).i(t)
Vp=17V e VRMS=12V
VEF
VP 310V
220V
2
2
Analise de Circuitos em Corrente
Alternada - Ed. Erica
A potência dissipada no resistor
será igual ao valor médio da
potencia instantânea
Ip= 4,25A IRMS=3A
P=VRMS.IRMS
No exemplo:
P=12V.3A=36W
Analise de Circuitos em Corrente
Alternada - Ed. Erica
11
Genericamente para qualquer circuito
Dado as tensões:
P VRMS .IRMS . cos
v1(t)=20.sen(w.t) (V)
v2= 5
0 0 (V)
V3=20+j15(V)
é o ângulo de defasagem entre a corrente e a tensão
No CASO DE CIRCUITO RESISTIVO
1) Representar as três tensões no DF
00
2) Obter
cos 00 1
2a) v4=v1+v3
P VRMS.IRMS
2b) v5=v1+v2+v3
3) As tensões V1 e V3 são aplicadas respectivamente em R=10 Ohms e
R=5 Ohms. Calcule em cada caso a) expressão de i(t) b) Potencia dissipada
mm cada caso.
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Capacitor
Capacitância (C)
Dispositivo usado para armazenar cargas elétricas
É a medida da capacidade que tem o dispositivo de armazenar cargas elétricas
Placas de area
S(m2)
terminais
O seu valor é especificado em Farads (F) e depende das dimensões (S, d) e do
material de que é feito o dielétrico (isolante que separa as duas placas).
Para um capacitor de placas planas e paralelas de área S, separadas por
Uma distancia d, a capacitância será dada por:
Dielétrico (isolante)
d(m)
C K . 0.
Símbolo
S
d
Onde ε0 é a permissividade dielétrica do vácuo
ε0=8,85pF/m
K é a constante dielétrica do material. Por exemplo: Vidro K=4,5, vácuo K=1
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Relação entre tensão (U), carga elétrica (Q) e capacitância (C) em um capacitor
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Tipo de Capacitores
Eletrolítico
U
Q +
+
Poliéster
Cerâmico
Q=U.C
C
- -
Q é a quantidade de cargas em Coulombs (C)
U é a tensão aplicada em volts (V)
C é a capacitância em Farads (F)
Tântalo
A quantidade de carga é diretamente proporcional a U e a C
Ex: se C=100µF
Q=100.10-6.10=
e
U=10V qual a carga armazenada?
10-3C=1mC
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
12
Capacitores Polarizados (Valor maior que 1uF)
Capacitores Não Polarizados (Valor menor que 1uF)
Eletrolíticos
Símbolo
0.1=0.1uF
Tântalo
100n=100nF=0,1uF
10 Numero: Primeiro Digito (1)
20 Numero: Segundo Digito (0)
30
C=1000pF=1nF
Numero: Numero de zeros (00)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Usando Código de Cores (Poliester)
Qual o valor da capacitância? Da tolerancia? Da máxima tensão?
Amarelo=4
Violeta=7
Laranja=3
Vermelho=2
Violeta=7
Preto=20%
Amarelo=4
Vermelho=250V
Valor=270000pF=270nF=0,27uF
Tolerância
20%
Máxima Tensão
5%
100V
10%
250V
Valor=47000pF=47nF=0,047uF
400V
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Capacitores Variáveis
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Capacitor em CC
No circuito, a chave é fechada em t=0, considerando que o capacitor está inicialmente
descarregado, VC(0)=0
VR=VCC
VR
I
t=0
Vcc
De acordo com a 2a Lei de Kirchhoff:
Trimmer
Em t=0
I ( 0)
I
VCC =VR + VC (em qualquer instante)
VR(0) + VC(0)=VCC >>>>>>>
VR ( 0 ) VCC
R
R
VC=0
VCC
VC
VR(0)=VCC
C começa a se carregar, VC começa a aumentar......
...e VR começa a diminuir, conseqüentemente I
Depois de um tempo (que depende de C e R), o capacitor estará carregado
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
13
Gráficos
Conclusões:
•Do ponto de vista físico não existe movimento de cargas (corrente) através do
capacitor (as cargas se movimentam no circuito externo)
•A corrente no capacitor está adiantada em relação à tensão
•O tempo de carga depende da constante de tempo do circuito definida como
sendo
=R.C, sendo C em Farads (F)
R em Ohms ( em segundos(s)
•Na pratica bastam 4 constantes de tempo para carregar um capacitor
VR=0
VC=VCC
I=0
VCC
Analise de Circuitos em Corrente
Alternada - Ed. Erica
R
C
+ +
- -
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Equações: Tensão no Capacitor e Resistor
Carga Total
e=base do logaritmo neperiano=2,71828........
Teoricamente, de acordo com a equação de vC(t), o capacitor estará totalmente
carregado para um tempo infinito.
VR
7,56V
vc(t)=VCC.(1-e-t/RC) (Função Exponencial)
VC
vR(t)=VCC.e-t/RC
4,44V
Na prática podemos considerar o capacitor carregado para t=44.R.C
Para t=4.R.C
vc(4.R.C)=VCC.(1-e-4)=0,98.VCC=11,76V
t=s
Para t=0
na expressão de vC(t)
na expressão de vR(t)
Para t= R.C=2s
vc()=VCC.(1-e-0)=0
vR(0)=VCC.e-0=VCC=12V
na expressão de vC(t)
na expressão de vR(t)
vc(R.C)=VCC.(1-e-1)=0,63.VCC=7,56V
vR(R.C)=VCC.e-1=0,37.VCC=4,44V
t=4.
t=
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Curva de Descarga
Descarga do Capacitor
Considerando o capacitor totalmente carregado com VC =VCC=12V
Como fazer para descarregar o capacitor ?
Vc=12.e-t/RC
Deve haver um condutor entre as placas para que ocorra a descarga
4,4V
Se for um fio a descarga será instantânea, caso contrario o tempo de descarga
dependerá da resistência.
Para t=RC a tensão em C cai para v(RC)=0,37.Vcc=0,37.12=4,4V
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
14
Associação de Capacitores
Paralelo
Serie
1
1
1
1
Ceq
C1 C2 C3
Para dois em serie:
C eq
C eq C1 C 2
C1 .C 2
C1 C 2
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Capacitores Polarizados
Capacitor em CA
Se a um capacitor ideal for aplicada uma tensão senoidal, a corrente resultante
será senoidal e adiantada de 900 em relação à tensão aplicada.
+ +
- -
+ +
100uF
- -
100uF
+ +
+ +
+ +
v(t)= vC(t) =VP.senwt
50uF
100uF
- -
100uF
50uF
+ +
- -
- -
+ +
- -
- -
+ +
100uF
100uF
- -
200uF
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Neste caso v(t)=VP.senw.t
ou
IC(t)=IP .sen(w.t+900)
ou
v=VP
00
IC=IP 900
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Exercício1: Calcule a intensidade da corrente no circuito em seguida desenhe
o diagrama fasorial, se a fase inicial da tensão é zero.
Reatância Capacitiva
É a medida da oposição oferecida pelo capacitor à passagem da corrente alternada
é calculada por:
XC
V
V0
V
90 jX C
I C I C 90 I C
Solução: Como são dados C e a freqüência, podemos calcular a
reatância capacitiva (Xc) :
com
C em Farads (F), f em Hertz (Hz)
resultando XC em Ohms (Ω)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
15
Calcular a intensidade da corrente para cada posição da chave.
A
B
I=4,5mA
110V/60Hz
V= 120V
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Triangulo das Tensões
Circuito RC Série
V
Num RC serie a corrente continua na frente da tensão mas de um angulo menor do
que 90º. Seja a fase da corrente igual a 900 (arbitrariamente).
I
V
VR
V 2 VR2 VC2
VR
VC
Dividindo todos os lados por I teremos um triangulo chamado de
Triangulo de Impedâncias
v
VC
Triangulo das Impedâncias
V/I
Ângulo de defasagem
cos = VR / V
logo
V
Z
I
VR/I
VC/I
= arccos(VR /V)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Impedância do circuito
VR
R
I
Resistência do circuito
VC
XC
I
Reatância do circuito
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Triangulo das Potências
Z 2 R 2 X C2
XC
Cos
z Z
Se no triangulo das tensões os lados forem multiplicados por I obtemos o que
É conhecido como Triangulo das Potências
R
Z
Z=R-jXC
PAp V .I
V.I
VR.I
R
Z
P VR . I
PR VC .I
VC.I
PAp=potência aparente (VA)
P=potência real (ativa)(W)
2
PAp
P 2 PR2
PR= potência reativa (VARC)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
16
Indutor
Chamamos de indutor a um fio enrolado em forma de hélice em cima de
um núcleo que pode ser de ar ou de outro material. A figura mostra o
símbolo para indutor com núcleo de ar, de ferro e de ferrite.
Força Eletromotriz Induzida
Para que uma tensão s eja induzida em uma espira ou em um enrolamento, é necessário que haja variação do fluxo
magnético através da espira ou do enrolamento. A figura a seguir mostra um exemplo de induç ão de tensão em um
enrolam ento (bobina).
A Lei de Lenz diz que o sentido da corrente induzida deverá ter orientação de tal forma que origine um campo
magnético variável que se opõe à variaç ão do fluxo magnétic o original.
Indutor em Corrente Contínua
O que acontece quando no circuito da Fig. 02 fechamos a chave no
instante t=0? A tensão é aplicada no indutor mas a corrente leva um certo
tempo para crescer, a explicação é um fenômeno chamado auto indução que
faz aparecer uma tensão e que se oporá ao crescimento da corrente.
Ao abrir a chave, no instante t2, novamente esse fenômeno vai atuar na
bobina não deixando a corrente se anular instantaneamente, fazendo aparecer
uma tensão e com a polaridade tal que se opõe à diminuição da corrente.
Observe que isso faz aparecer uma tensão nos terminais da chave que é igual a
E + e, que pode causar uma arco de corrente.
Concluímos que um indutor se opõe à passagem de uma corrente alternada (se
opõe à variação de uma corrente) e que a corrente está atrasada em relação
à tensão (a tensão já está aplicada e a corrente começa a aumentar).
A indutância (L) de um indutor é um parâmetro que dá a medida da
capacidade que tem o indutor de armazenar energia no campo magnético, a
sua unidade se chama Henry (H).
Fig04: Indução de tensão provocada pela v ariaç ão da intensidade do cam po m agnético de um imã
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Indutor em Corrente Alternada Senoidal
A corrente em um indutor está atrasada em relaç ão à tens ão em um circuito CC. O que acontece se alimentarmos um
indutor ideal (não tem resistência ôhmica) de indutância L c om uma tensão alternada senoidal de freqüência f ?
Obs: Um indutor ideal (que não existe) não tem resistência ôhmica (R).
No circuito da Fig04, a corrente continua atrasada em relação à tensão e de um angulo bem definido, no caso 90º.
Observe que a fas e da tensão foi considerada arbitrariam ente igual a 0º.
( a)
(b)
(a)
(c)
Fig02: Indutor em CC ( a ) Instante que a chave é fechada ( b )
Corrente em regime ( c ) Instante que a chave é aberta
Analise de Circuitos em Corrente
Alternada - Ed. Erica
1.4. Reatância Indutiva
Como vimos um indutor se opõe à variação de uma corrente. A medida desta oposição é dada pela sua reatância
indutiva (XL ), sendo calculada por:
(b)
Fig04: Indutor em CA - (a) circ uito; (b) diagrama fasorial (fasor em vermelho: corrente; fasor preto: tens ão)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Circuito RL Serie
Na prática um indutor apresenta resistência ôhmica, portanto, em um
Indutor a corrente sofre dois tipos de oposição:
IMPORTANTE !!!!!
•A resistência ôhmica do fio (R) que tende a manter tensão e corrente em fase
Com L especific ado em Henries (H), f em hertz ( Hz ), XL em ohms (
).
Exercício1: Uma bobina tem 0,1 H de indutância, sendo ligada a um a tensão de 110V, 60Hz. Determinar:
a) Reatância da bobina (XL ) b ) Valor da corrente no c ircuito ( I )
Solução:
a)
XL = 2. .60.0,1 = 37,7
b) I = V / XL = 110 / 37,7 = 2,9A
•A reatância indutiva (XL) que tende a defasar tensão e corrente em 900
A combinação dos efeitos da resistência com da reatância é chamado de.......
Impedância (Z)
A corrente ainda continua atrasada em relação à tensão mas de um ângulo
menor do que 900
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
17
Circuito RL serie
Diagrama Fasorial
Impedância Indutiva (ZL)
V
VL
VR
A oposição que um indutor real oferece à passagem de uma corrente
Alternada é uma combinação da resistência ôhmica com a reatância
Indutiva sendo chamada de impedância
I
I
I
Considerando a fase da corrente nula
v
v
Numero
complexo
Numero
complexo
Z
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Relações no Circuito RL Serie
i=I
V
VL
VR
Impedância na Forma Polar
00
V
vL=VL
900
vR=VR
0o
xL=XL
900 = jXL =
I
Modulo:
VL
I
VR
I
V VR VL
I
I
I
V=VR + VL dividindo por I
IMPEDANCIA
NA FORMA
CARTESIANA
VL
VR
Z
R 2 X L2
I
arctg
Fase:
00 = R =
r=R
Z R jX L
Numero
complexo
V
I
XL
R
ou
arccos
R
Z
Portanto..............
z=Z
Ou na forma polar.........
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Exemplo: Dado o circuito pedem-se:
Analise de Circuitos em Corrente
Alternada - Ed. Erica
a) A impedância na forma cartesiana é Z=30+j40 (Ω)
Na forma polar:
O modulo de Z
a) Valor da impedância e sua representação nas formas polar e cartesiana
A fase de Z
Z 30 2 40 2 50
arctg
b) Valor de da indutância
40
530
30
c) Valor da corrente e sua representação nas formas polar e cartesiana
d) Valor de VR e VL e suas representações na forma polar e trigonométrica
e) Diagrama fasorial
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Z=50
530 (Ω)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
18
VR=R.I= 30 00 .
d)
b) Pela reatância indutiva tira-se L
40
106mH
2. .60
L
X L 2. . f .L
2,2 370 = 66
VR = 66
VL=XL.I= 40 900 .
370
370
(V)
(V)
2,2 370 = 88
1270
(V)
c) Corrente no circuito
I
v 11090 0
2,237 0 ( A)
Z
50530
VL= 88
1270
(V)
0
vR (t ) 66. 2 .sen( 2. .60 .t 37 ) 66. 2 .sen(377.t 37 0 )(V )
i=2,2.cos370 + j2,2.sen370 =1,75 +j1,32 (A)
v L (t ) 88 . 2 .sen (377 .t 127 0 )(V )
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Potencia Em um Circuito RL Serie
e) Diagrama Fasorial
Para a analise da potencia seja o triangulo de tensões do diagrama fasorial
V(110V)
Multipliquemos cada um dos lados por I, resultará o triangulo de potencia
530
V.I
VL(88)V
1270
I(2,2A)
VR(66V)
V
VL
VL.I
370
VR
I
VR.I
I
P=VR.I=V.I.cos é a potência real ou ativa do circuito (W)
PAP=V.I é a potencia aparente do circuito (VA)
PR=VL.I=V.I.sen é a potencia reativa do circuito (VARi)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Triangulo de Potencias
P=PAP.cosΦ=V.I.cos Φ
Carga Puramente Resistiva
PAP =V.I
PR=VL.I
2
PAP
P 2 PR2
Φ=0 portanto cos Φ=1 a carga aproveita toda a energia fornecida
Pelo gerador
Carga Puramente Indutiva
P=VR.I
Φ=90 portanto cos Φ=0 não há potencia ativa a carga troca
energia entre o gerador.
Fator de potencia
Carga Indutiva e Resistiva
É UMA MEDIDA DO APROVEITAMENTO DA ENERGIA
È definido como sendo
FP= cosΦ=
Φ<90 portanto cos Φ<1 há potencia ativa a carga aproveita
apenas uma parte da energia fornecida.
P
PAP
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
19
1) A potencia consumida (ativa) por uma instalação elétrica
é de 2400W. Se a tensão de alimentação é 220V, calcular a
potencia aparente e corrente quando:
a) FP=0,9
3) No circuit0 a leitura dos instrumentos é V=220V. I=55A e
P=10KW.
Calcular: a ) Impedância do circuito b) Valor da resistência e
indutância (f=60Hz) c) Potencia aparente e reativa d ) FP
b) FP=0,6
2) Um circuito consome 10A, quando ligado em 220V. Um
wattimetro ligado ao circuito indica 2000W. Calcular o fator
de potencia do circuito e a potencia reativa.
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
4) No circuito VR(t)=10.sen(ω.t-300)(V). Determinar:
a) i(t)
b) v(t)
Circuitos Mistos
Para resolver um circuito misto, deveremos
primeiramente calcular a impedância equivalente,
para em seguida calcularmos todas as
correntes e tensões. Portanto é um procedimento
semelhante ao adotado na analise de circuitos
resistivos, somente que agora temos elementos
reativos presentes, sendo necessário usar como
ferramenta de analise os números complexos.
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Exemplo: Resolver o circuito
IT
I1=IT
I3
Z5 = Z3 + Z4 = 10 -j10 ( ) = 14,1 -45º()
Z2 = 20
90º ()
I2
Z6 = Z2 // Z5 = (Z2.Z5)/(Z2 + Z5 )= (20
Analise de Circuitos em Corrente
Alternada - Ed. Erica
90º x14,1
- 45º )/(j20 + (10- j10) =(282 45o )/(10+j10)
Analise de Circuitos em Corrente
Alternada - Ed. Erica
20
Calculo das Correntes
Z6= (282
45º )/14,1
45º ) =20
0º =20 ()
I1 = V/ZE =( 50
0º )/(22,36
-26,5º) = 2,24
26,5º (A)
I1
-26,5º( )
ZE = Z1 + Z6 = -j10 + 20 = 20 - j10 = 22,36
U6 =Z6.I1=20
0º x 2,24
I3
26.5º = 44,8 26.50 (V) e como
U6 = U2 =U5 então
U6
I2 =( 44,8
26,5º )/(20
90º)=2,24
I3 =( 44,8
26,5º )/(14,1
I2
- 63,5º (A)
-45º ) = 3,17
71,5º (A)
O Fator de potencia do circuito é:
FP=coscos26,5º=0,895
E a Potencia real:
P = U. I.cos = 50.2,24.cos26,5º = 100W
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Correção do Fator de Potência
POR QUE CORRIGIR?
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Correção do Fator de Potência
Situação Desejável
•DIMINUIÇÃO DA CORRENTE NA LINHA DE ALIMENTAÇÃO.
•MULTA DA CONCESSIONARIA
Situação Atual:
Antes da correção
FP=cosΦ2>0,92 ADEQUADO
FP=cosΦ1<0,92 INADEQUADO
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Exemplo
Cálculo do Capacitor
C
Calcular C no circuito para que o FP do circuito aumente para 0,94
P
.(tg1 tg 2)
w.V 2
Calcule o FP
Obs: ver a dedução na bibliografia
O FP aumenta de cosΦ1 para cos Φ 2
F.P atual =0,662
P é a potência ativa (Watts) do circuito,
P = UxIxcos Φ 1 =220x14,46x0,662 =2108W
w é a frequência angular
Deseja-se cosΦ1 =0,662 >>>>>> cosΦ2 =0,94
V é o valor eficaz da tensão
Faça download do arquivo Exemplo usando microcap e execute no
seu PC se tiver instalado o software MicroCap9
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
21
Conclusão
Observe o que acontece quando ligamos o capacitor de 75uF. A corrente na carga
não muda, mas a corrente na linha diminui. Esse é o objetivo, diminuir a
corrente na LINHA, mantendo as condições da carga (por exemplo um motor continuará
operando com a mesma potência) e consumindo a mesma corrente
Circuitos Trifásicos
SÃO NECESSARIOS QUANDO A CARGA CONSOME MUITA POTENCIA
(CORRENTE E TENSÃO ALTA).
AS TRES TENSÕES SÃO DEFASADAS ENTRE SI DE 1200
CARGA E GERADOR PODEM SER LIGADOS DE DUAS FORMAS: ESTRELA E
TRIANGULO.
CONSIDERAREMOS SOMENTE CARGA BALANCEADA (AS TRES
IMPEDANCIAS SÃO IGUAIS)
A corrente de linha diminui para 10,56A
Mas a corrente na carga se mantem no mesmo valor 14,47A
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
LIGAÇÃO ESTRELA
Corrente de Fase: IA,IB,IC
VCA
VA=VF
IN
Corrente de Linha: corrente na linha que liga o gerador à carga
Para a Ligação estrela: IF=IL
VC
VAB=VL
VB
Relação entre tensão de fase (VF) e tensão de linha (VL)
VCB
Tensões de Fase (TENSÃO DO GERADOR): VA=VB=VC=VF
VL 3 .VF
Tensões de Linha( TENSÃO ENTRE AS LINHAS): VCA=VCB=VAB=VL
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Considere que no circuito Z1=Z2=Z3= 10 Ohms resistiva
Analise de Circuitos em Corrente
Alternada - Ed. Erica
LIGAÇÃO TRIANGULO
A
Calcular: a)Tensões de fase e de linha
b) Correntes de fase, de linha e no neutro
IAC=IF
B
C
120V/fase 0
IN
Tensões de Fase: VCA, VAB, VBC
VF=VL
120V/fase -120
RELAÇÃO ENTRE AS CORRENTE DE LINHA E DE FASE
120V/fase 120
IL 3 .IF
Analise de Circuitos em Corrente
Alternada - Ed. Erica
Analise de Circuitos em Corrente
Alternada - Ed. Erica
22
No circuito Z1=Z2=Z3= 20 Ohms (Resistiva)
a) Calcular a corrente na carga em cada fase
b) Calcular a corrente de linha
380V fase1200
380V fase 0
380V fase -1200
Analise de Circuitos em Corrente
Alternada - Ed. Erica
23