Força Magnética

Forças de Campo
Força
Magnética
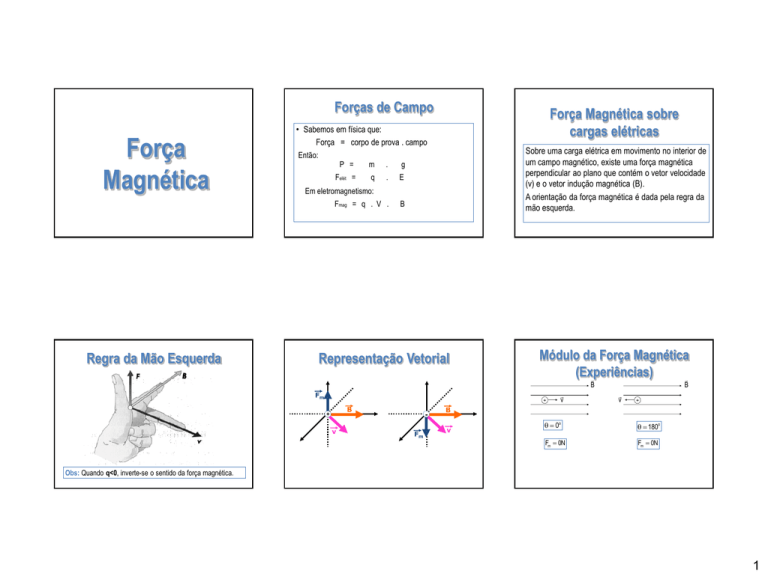
Regra da Mão Esquerda
Força Magnética sobre
cargas elétricas
• Sabemos em física que:
Força = corpo de prova . campo
Então:
P =
m
.
g
Felét =
q
.
E
Fmag = q .? V .
B
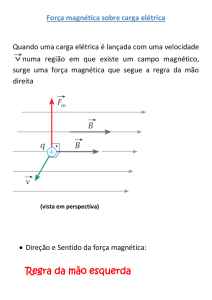
Sobre uma carga elétrica em movimento no interior de
um campo magnético, existe uma força magnética
perpendicular ao plano que contém o vetor velocidade
(v) e o vetor indução magnética (B).
A orientação da força magnética é dada pela regra da
mão esquerda.
Em eletromagnetismo:
Representação Vetorial
Módulo da Força Magnética
(Experiências)
B
Fm
+
B
+
v
Fm
v
B
v
+
B
v
  0o
  180o
Fm  0N
Fm  0N
Obs: Quando q<0, inverte-se o sentido da força magnética.
1
Módulo da Força Magnética
(Experiências)
Módulo da Força Magnética
(Experiências)
B
B
vx
+
Fm
  90o
v
+
Fm  máx
Caso Particular
  90o
B
Fmag  FRcp
q.V.B  m.acp
V2
q.V.B  m.
R
Fm
+
v

m.v
R
q.B
Fm  q .v.B.sen
B
+
v
Módulo da Força Magnética
v
0o    90o
vy
Fm  q .v y .B
e
v y  v.sen

Fm  q .v.B.sen
Caso Particular
Sob efeito exclusivo da força magnética a carga executa
um movimento circular uniforme, onde:

v
R
Como  
1
Mas, T 
f

2.
T
v
m.v
q.B

q.B 2.

m
T
q.B
f
2..m
q.B
m
T
•
•
•
•
|q| é o módulo da carga elétrica;
v é o módulo da velocidade da carga;
B é o módulo do vetor indução magnética;
θ é o ângulo formado entre a velocidade (v) e o vetor
indução magnética (B).
Força Magnética sobre
cargas elétricas
Fm  q .v.B.sen
Se   90o :
R
m.v
q.B

q.B
m
T
2..m
q.B
f
q.B
2..m
2..m
q.B
2
Força Magnética sobre fios
condutores
Sobre um fio condutor percorrido por corrente,
imerso no interior de um campo magnético,
manifesta-se uma força magnética
perpendicular ao plano que contém o fio e o
vetor indução magnética (B).
Origem da força
Origem da força
Regra da Mão Esquerda
• No elétron em movimento no fio haverá uma força
magnética perpendicular ao fio cujo sentido é definido
pela regra da mão esquerda, se pensarmos no
sentido convencional da corrente perceberemos que o
sentido da força será o mesmo.
• Essa força atua sobre cada elétron que percorre o fio.
• Então o condutor estará sujeito à ação de uma força
magnética F, que é a resultante de todas essas forças
sobre cada partícula.
i
Módulo da Força Magnética
sobre fios condutores
Fm  q .v.B.sen
fica Fm  q .
e
v
L
.B.sen
t
L
t
mas
Substituindo, temos: Fm  i.L.B.sen
 Fm  B.i.L.sen
Módulo da Força Magnética
i
q
t
Fm  B.i.L.sen
•
•
•
•
B é o módulo do vetor indução magnética
i é intensidade da corrente
L é o comprimento do fio
θ é o ângulo formado entre o fio e o vetor indução
magnética (B)
3
Força magnética entre dois
condutores
Módulo da Força Magnética
entre dois condutores
O campo magnético do
fio 1 faz força
magnética sobre i2.
O campo magnético do
fio 2 faz força
magnética sobre i1.
F1,2  B1.i2 .L
F2,1  B2 .i1.L
.i1
.i2 .L
2..d
.i .i .L
F1,2  1 2
2..d
F1,2 
• Direção: Perpendicular aos fios
• Sentido: Atração (correntes de mesmo sentido)
Repulsão (correntes de sentidos opostos)
.i2
.i1.L
2..d
.i .i .L
F2,1  2 1
2..d
F2,1 
Módulo da Força Magnética
entre dois condutores
Fm 
•
•
•
•
.i1.i2 .L
2..d
µ é a permeabilidade magnética do meio;
i1 e i2 são as correntes nos fios condutores;
L é o comprimento de interação dos fios condutores;
d é a entre os fios condutores.
4