Integral Definida ou de Riemann

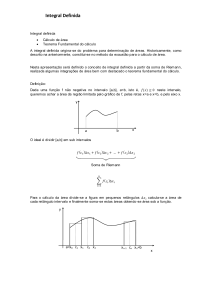
CAPÍTULO 7 - INTEGRAL DEFINIDA OU DE RIEMANN
7.1- Notação Sigma para Somas
A definição formal da integral definida envolve a soma de muitos termos, para isso introduzimos o conceito de
somatório ( ∑ ).
Exemplos:
n
1+ 2 + 3 + 4 +L+ n = ∑k =
k =1
n( n + 1 )
2
n
12 + 2 2 + 3 2 + 4 2 + L + n 2 = ∑ k 2 =
k =1
~
soma de inteiros sucessivos
n( n + 1 )( 2n + 1 )
~ soma de quadrados sucessivos
6
A integral de Riemann de uma função f (x ) num intervalo [a ,b] , é equivalente à soma de todos os elementos de área
sob a curva f (x ) , ou seja:
[c k , f (c k )]
Y
.............................
[c n , f (c n )]
......................
ck
Ak
cn
X
x k − x k −1
x n − x n −1
Soma das áreas parciais sob a curva que fornece a área total sob a curva.
onde:
c k coordenada entre x k −1 e x k
f (c k ) ordenada de c k (altura do retângulo)
∆x k = x k − x k −1
(base do retângulo)
A área do k − ésimo retângulo é dada por Ak = f (c k ) ⋅ ∆x x somando-se todas as áreas dos retângulos sob a
curva f (x ) , tem-se uma aproximação (devido às quinas dos retângulos) da área sob a curva. Quanto menor for ∆x k ,
melhor é a aproximação.
Assim:
n
∑ f ( ck )∆xk = área sob a curva f (x ) = A .
||∆x ||→0
lim
k
k =1
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
120
7.2- Integral Definida de Riemann
Definição: Seja f (x ) uma função contínua num intervalo [a ,b] , então se o limite
n
∑ f ( ck )∆xk
||∆x ||→0
lim
k =1
k
existe, a função f (x ) é integrável em [a ,b] no sentido de Riemann, e é definida por
n
lim
||∆xk ||→0
∑
k =1
b
f ( c k )∆x k = ∫ f ( x )dx ,
a
onde a integral definida de f (x ) , no intervalo [a ,b] , dará uma nova função g (x ) calculada no intervalo [a ,b] , o que é
escrito na forma g (x ) ba , ou seja, g( x ) ba = g( b ) − g ( a ) , assim:
b
∫ f ( x )dx = g( b ) − g( a )
a
7.3- Teorema Fundamental do Cálculo
Se f for integrável em [a,b] e se F for uma primitiva de f em [a,b], então
∫a f ( x )dx = [g( x )]
b
b
a
b
= g( x )
= g( b ) − g( a )
a
7.3.1Existência da Integral de Riemann de uma função Contínua
Teoremas
a)
[ ]
[ ]
Se f ( x ) é uma função contínua no intervalo fechado a, b , então f ( x ) é Riemann - integrável em a, b .
[ ]
b) Se f ( x ) é uma função limitada e seccionalmente contínua no intervalo fechado a, b , então f ( x ) é Riemann –
[ ]
integrável em a, b .
Exemplos:
1/x ; x>0
x2 +1 ; x>0
f(x) =
f(x) =
y
1
se x ≤ 0
1
f(x)
se x ≤ 0
y
f(x)
2
1
1
x
a
b
Função limitada seccionalmente e
Contínua em [a ,b] , é R - integrável
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
x
a
b
Função ilimitada seccionalmente
em [a ,b] , não é R - integrável
121
Exercícios
1) Determinar a área limitada pela curva y = 5 x − x 2 e pelo eixo x.
5x −x 2 = 0
x( 5 − x ) = 0
y = 5x − x 2
x = 0

x = 5
0
5
A = ∫ 5 x − x 2 dx = 5.
0
5
x2 x3
−
2
3
5
=
0
53 53 5
−
= u .a .
2
3 6
2) Determinar a área limitada pelas curvas y = 5x – x2 e y = 2x.
y
y = 2x
y = 5x – x2
0
3
x
5
- Pontos de interseção
- Área
3
 y = 5x − x 2

 y = 2 x
∫
A = (5x − x 2 − 2 x )dx
0
3
2 x = 5x − x 2
∫
A = (3x − x 2 )dx
x 2 − 3x = 0
x ( x − 3) = 0
0
3x 2 x 3
A=
−
2
3
x = 0

x = 3
3
0
27
A=
−9
2
9
A = u.a.
2
3) Determinar a área limitada pelo eixo y e pela curva x = 4 – y2
y
x = 4 − y2
2
4 − y2 = 0
y = ±2
A1
x
y = 4−x
-2
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
122
4
∫
A = 2.
4 − x dx
0 4243
1
A1
4
∫
A = −2.
2
∫
1
(4 − x ) 2 .(−1)dx
A = 2 (4 − y 2 )dy
0
0
A=
3

−24 − x 2 .

2

y3 
A = 2.4 y − 
3 

0
4
2

3
0
ou
 8
A = 2.8 − 
 3
32
A=
u.a.
3
2
A = −2. .[− 8]
3
32
A=
u.a.
3
4) Determinar a área limitada pelas curvas y2 = 4ax; x + y = 3a; y = 0; primeiro quadrante e “a” positivo.
y
x=
a
3a
y=0
y2
4a
x
x = 3a − y
-2
- Pontos de interseção
 y 2 = 4ax

x + y = 3a → x = 3a − y
y 2 = 4a (3a − y)
y 2 − 12.a 2 + 4ay = 0
y 2 + 4ay − 12a 2 = 0
− 4a ± 16a 2 + 48a 2
2
− 4a ± 8a
y=
2
 y = 2a

 y' = −6a
y=
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
- Área
2a
A=
∫
0
(3a − y −
y2
)dy
4a
2a

y2 y3 
A = 3ay −
−

2 12a 

0
1
A = 6a 2 − 2a 2 −
.8a 3
12a
2
A = 4a 2 − a 2
3
2
10.a
A=
u.a.
3
123
5) Calcule a área compreendida entre o eixo X e a curva f (x ) =
(
)
1 2
x − 2 x + 8 entre [− 2 , 4 ] .
8
O gráfico da curva é:
f (x )
Y
1
8
-2
-1 0
1 2 2
3
4
X

 4 1 43
1  x3
x2
4
− 2 )3
− 2)2
(
(
x − x − 8 dx =  − 2
+ 8(x) =  − 2
+ 8(4 ) −
−2
+ 8(− 2)
2
3
2
8  3
2
 −2 8  3

∫−2 (
4
)
2
1 43
42
(− 2 )3 − 2 (− 2 )2 + 8(− 2 ) = 1  64 − 2 16 + 32 + 8 − 2 4 − 16 
+ 8(4 ) −
 −2



8  3
2
3
2
2
3
2

 8  3
2 3
 16
 16 2 3 16 + 2 − 3 15
.
=
 6 − 2 + 4 + 6 − 6 − 2 = 6 + 6 − 6 =
6
6


6) Avalie diretamente a integral de Riemann dada pelo cálculo de um limite das somas de Riemann. Use partições
cosntituídas de subintervalos de comprimentos iguais e use retângulos inscritos ou circunscritos, conforme esteja
indicado.
2
a.
∫x
0
0
b.
3
∫x
dx (retângulos inscritos)
2
dx (retângulos circunscritos)
−2
2
(
)
c. ∫ x 3 + 2 dx (retângulos inscritos)
0
−1
d.
∫ (x
2
)
− x − 2 dx (retângulos inscritos)
−2
7.4- Propriedades Básicas da Integral Definida
1) Integral de uma função constante
Se f ( x ) = k , k constante, então
b
∫
a
b
f ( x )dx = ∫ kdx = kx ba = k ( b − a ) , como mostra a Figura
a
Y
f (x ) = k
A
0
a
b−a
X
b
Área sob uma função constante.
2) Homogeneidade
b
b
a
a
∫ kf ( x )dx = k ∫ f ( x )dx , onde k é uma constante
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
124
3) Aditividade
b
b
b
a
a
a
∫ [ f ( x ) + g( x )] dx = ∫ f ( x )dx + ∫ g( x )dx
4) Linearidade
b
b
b
a
a
a
∫ [ Af ( x ) + Bg( x )] dx = A∫ f ( x )dx + B ∫ g( x )dx , com A e B constantes.
5) Positividade
Se f é uma função Riemann - integrável em
[a, b]
e se f(x)>=0 para todo x no intervalo
[a ,b] ,
então
b
∫a f ( x )dx ≥ 0
6) Comparatividade
Se f e g são Riemann - integráveis em [a ,b] e se f(x) ≤ g(x) para todo x no intervalo [a ,b] , então
b
∫
a
b
f ( x )dx ≤ ∫ g( x )dx
a
y
max de g(x)
M
min de g(x)
m
y = g(x)
y = f(x)
a
b−a
x
b
7) Valor Absoluto
b
∫
a
b
f ( x )dx ≤ ∫ | f ( x ) | dx
a
Prova: Assumindo que f e | f | são Riemann - integráveis no intervalo [a ,b] .
Temos que - | f(x) | ≤ f(x) ≤ | f(x) |
( -|x| ≤ x ≤ |x| )
b
Então
a
Logo
b
b
b
b
b
a
a
a
a
a
∫ − | f ( x ) | dx ≤ ∫ f ( x )dx ≤∫ | f ( x ) | dx ; isto é: − ∫ | f ( x ) | dx ≤ ∫ f ( x )dx ≤∫ | f ( x ) | dx
b
b
a
a
∫ f ( x )dx ≤ ∫ | f ( x ) | dx
8) Aditividade com relação ao intervalo de integração
Se f é Riemann - integrável no intervalo [a ,b] , bem como no intervalo [b , c ] , então f é também Riemann integráveis no intervalo [a , c ] , ou seja:
c
∫
a
b
f ( x )dx = ∫ f ( x )dx +
a
c
∫ f ( x )dx
b
Definições:
(i)
Se f é uma função qualquer e a é um número no domínio de f, definimos:
a
∫ f ( x )dx = 0
a
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
125
(ii)
Se a > b e f é Riemann - integráveis em [b, a], então definimos:
b
∫
a
a
f ( x )dx = − ∫ f ( x )dx
b
7.5- Teorema do Valor Médio para Integrais
Se f é contínua em [a,b], então existe um número c em [a,b] tal que
b
f( c ).(b - a) =
f( c ) =
1
b−a
∫ f ( x )dx
y
ou
a
b
∫
f
f(c )
f ( x )dx
a
min f ≤ c ≤ max f
a
c
b
x
Ponto c do teorema do valor
médio
obs: A área sob a curva y = f(x) entre x = a e x = b é igual a área do retângulo cuja base é (b-a) e altura f(c).
Ex: Seja f(x) = x2, achar c no intervalo [1,4]
f( c ) =
1
4 −1
4
∫x
2
1
dx =
1  x 3 4  1  4 3 13  1  64 − 1  1
=
− = 
 = ( 21 ) = 7
3  3 1  3  3
3  3 3  3
Logo f( c ) = c2 = 7 → c =
(1 ≤ 2,65 ≤ 4)
7 = 2,65
7.6- Teorema Fundamental do Cálculo (TFC)
A primeira parte deste teorema afirma que as operações de diferenciação (derivação) e integração são inversas
uma da outra, isto é, diferenciação desfaz a integração e vice-versa.
O enunciado do TFC é composto de duas partes. Assim, se f é contínua num intervalo I tal que a∈I e b∈I, e seja x∈I,
então:
x
dy d
=
f ( t )dt = f ( x )
dx dx ∫a
1a parte:
"a derivada da integral é o integrando"
x
onde y =
∫ f ( t )dt
a
2a parte: Se g é uma primitiva (anti-derivada) de f, de tal forma que g'(x) = f(x), então
b
∫ f ( x )dx = g( b ) − g( a ) , para todo x em [a,b]
Exemplos: (1a parte) Calcular
x
a)
a
Se y = ∫ ( 2t 2 − t + 1 )dt , calcular
0
dy
.
dx
x
dy
d
=
( 2t 2 − t + 1 )dt = 2 x 2 − x + 1
dx ∫0
dx
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
126
x
b) Se y =
1
∫ t 3 + 1 dt , calcular
0
dy
.
dx
x
dy
d
1
1
=
dt = 3
dx dx ∫0 t 3 + 1
x +1
x2
c)
Se y =
∫ ( 5t + 7 )
25
dy
.
dx
dt , calcular
0
Fazendo u = x2 → du = 2xdx →
Por enquanto, podemos calcular
du
= 2x
dx
dy
du
u
dy
d
=
( 5t + 7 ) 25 dt = ( 5u + 7 ) 25 = ( 5 x 2 + 7 ) 25 (voltando o valor u = x2)
du du ∫0
logo:
dy
= ( 5 x 2 + 7 ) 25
du
Aplicando a Regra da Cadeia, temos:
dy
dy dy du
=
= ( 5 x 2 + 7 ) 25 (2x) →
= ( 5 x 2 + 7 ) 25 (2x)
.
dx du dx
dx
Exemplos de Integrais Definidas (2a parte do TFC)
1
3
 x3
 1  13
 

2

 =  + 1 −  ( 0 ) + 0  = 4 - 0 = 4
x
a)
(
x
1
)
dx
=
+
+
∫
 3
0  3
  3

3
3



 

0
4
b)
∫
4
1 
 1
x 
 − 12
2 dx


=
−
−
dx = ∫ 
dx
x
x


∫


x
x
x


1
1
1− x
1
4
3 
 12
x 2  4  12 2 3 2  4
x
= 
−
=  2x − x 
3  1 
3
 1
1
2 
 2
1
2 3   1
2 3 

=  2.4 2 − .4 2  −  2.1 2 − .1 2 
3
3


 
16
2
4
4
8


 
= 4 −
 − 2 −  = − − = −
3  
3
3 3
3

Observações:
•
•
1
x
x
x
=
=
1
x
1/ 2
x
1/ 2
x
= x 0 −1 / 2 = x −1 / 2
(1 = x0)
= x 1−1 / 2 = x +1 / 2
•
4 1/2 = (22 (1/2) ) = 2
•
4 3/2 = (22 (3/2) ) = 23 = 8
Disciplina de Cálculo Diferencial e Integral I
Prof. Salete Souza de Oliveira Buffoni
127