Testes de Hipóteses

Testes de Hipóteses
Júlio Osório
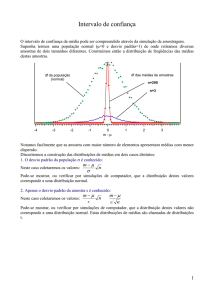
Os dois campos da Análise Estatística
Métodos
Estatísticos
Estatística
Descritiva
Inferência
Estatística
Estimativa
Testes de
Hipóteses
1
Exemplo Ilustrativo
Mediram-se os consumos de oxigénio (em ml)
durante a incubação de uma amostra aleatória de
15 suspensões celulares.
A partir dos dados obtidos, calculou-se
média=13.43 ml e variância=1.644 ml2.
O investigador pretende-se averiguar se os dados
fornecem evidência suficiente para se concluir, ao
nível de 5%, que a média dos consumos de O2 da
população de suspensões celulares excede 12 ml.
Questão: Há evidência na informação colhida na
amostra para se concluir, com uma margem de erro
de 5%, que os consumos de oxigénio na população
de suspensões celulares excede 12 ml?
Exemplo Ilustrativo: As Hipóteses
Etapas
1.
Enunciar estatísticamente a
questão de interesse
Exemplo
1.
O consumo excede 12 ml a
nível da população?
µ > 12 ml
2.
2.
Enunciar o oposto
3.
Formular a hipótese alternativa3.
4.
Formular a hipótese nula
Deve ser mutuamente exclusivo
e exaustivo.
µ ≤ 12 ml ⇔ µ = 12 ml
Teste de Hipóteses
4.
Tem o sinal ≠, <, ou >.
H1: µ > 12 ml
Tem habitualmente sinal =.
H0: µ = 12 ml
H0: µ = 12 ml
H1: µ > 12 ml
2
Hipótese Nula e Hipótese Alternativa
Uma hipótese é uma suposição acerca de um parâmetro de uma
ou várias populações (média, µ; variância, σ2; proporção, Π; ...).
A hipótese nula (H0) é sempre expressa por uma proposição de
não diferença. Representa sempre o status quo, isto é, a sua
não rejeição no teste de hipóteses implica que nenhuma
decisão de mudança seja tomada no processo em
investigação. Tem sempre o sinal de igual : =, ≤, ou ≥.
A hipótese alternativa (H1 ou Ha) é a hipótese de trabalho do
investigador, isto é, aquilo de que ele suspeita e está a tentar
provar. É habitualmente expressa por uma proposição de diferença,
e quando o teste conclui pela sua aceitação, mudanças de acção ou
de opinião sobre o processo serão tomadas. Tem sempre o sinal
de: ≠, <, ou >.
A hipótese nula nunca pode ser “aceite” com base nos resultados
de um único teste: não existe nenhuma maneira de determinar se
H0 é verdadeira. É mais correcto concluir “não se pode rejeitar H0”
do que concluir “aceitar H0”.
Testes Unilaterais
• A hipótese alternativa especifica um sentido para a
diferença (maior ou menor que).
H0: µ = µ0
H1: µ < µ0 ou µ>µ
µ0
• A probabilidade α concentra-se toda numa extremidade
da distribuição (esquerda ou direita)
Nível de Confiança
Região de
Rejeição
α
1-α
Região de
Não Rejeição
Valor
Crítico
µ0
Estatístico Critério
do Teste
Este teste é UNILATERAL ESQUERDO!
3
Testes Bilaterais
• A hipótese alternativa não especifica um sentido para a
diferença (maior ou menor que).
H0: µ = µ0
H1: µ ≠ µ0
• A probabilidade α é dividida ao meio, considerando-se
α/2 em cada uma das extremidades da distribuição
Nível de Confiança
Região de
Rejeição
Região de
Rejeição
1-α
1/2 α
1/2 α
Região de
Não Rejeição
Valor
Crítico
µ0
Estatístico Critério
Valor do Teste
Crítico
Erros no Teste de Hipóteses
Num teste de hipóteses podem ser cometidos dois tipos de erro:
Erro de Tipo I (1ª espécie) – ocorre quando a informação contida
na amostra conduz à rejeição de uma hipótese nula que é, na
realidade, verdadeira. Á probabilidade de se cometer o Erro I dá-se o
nome de nível de significância do teste, anotado por α.
Erro de Tipo II (2ª espécie) – ocorre quando a informação contida
na amostra conduz à não rejeição de uma hipótese nula que é, na
realidade, falsa. A probabilidade de se cometer o Erro II é
habitualmente anotada por β.
Chama-se Poder do Teste à probabilidade de se não cometer o Erro
II nesse teste, isto é, à capacidade que ele tem para rejeitar uma H0
que é realmente falsa. Anota-se habitualmente por (1-β). É desejável
que (1 - β) seja tão elevado quanto possível (≥ 0,80).
4
Erros no Teste de Hipóteses
A nível da População, H0 é
realmente:
Decisão Tomada
sobre H0:
Verdadeira
Falsa
Erro Tipo I
Rejeitar H0
Não Rejeitar H0
P (Erro I) = α
=nível de significância
Decisão Correcta
P = 1- β
= Poder do Teste
Decisão Correcta
P = 1- α
Erro Tipo II
P (Erro II) = β
Notas sobre α e β
O nível de significância α não é fixado por qualquer regra ou dedução
matemática: é adoptado pelo investigador.
Deve-se estar consciente de que, quanto maior for α, maior é o risco de se
rejeitar uma H0 que é, de facto, verdadeira.
Alguns investigadores rejeitam H0 se P ≤ 0,10, ao passo que outros exigem P ≤
0,05, P ≤ 0,01 ou até mesmo P ≤ 0,001 para declarar H0 como falsa. A adopção
de α é muitas vezes função da área específica de trabalho do
investigador.
O nível de significância de 5% (α
α = 0,05) é o mais popular, talvez apenas
porque Karl Pearson o adoptou quando publicou as primeiras Tabelas Estatísticas.
Ao contrário de α, β não pode ser fixado pelo investigador: não é,
habitualmente, nem especificado, nem conhecido.
É importante saber que, para um dado tamanho da amostra (n), α e β
guardam entre si uma relação inversa. Isto é, quanto mais baixa for a
probabilidade de cometer o Erro I, tanto maior será a probabilidade de cometer o
Erro II, e a única maneira de reduzir simultaneamente ambos é aumentar n.
Para um dado valor (fixado) de α, tamanhos maiores da amostra
conduzirão a testes com maior poder (1 – β ). A solução para este dilema é
encontrar uma situação de equilíbrio entre as duas probabilidades de erro.
5
O valor p (“p-value”)
O valor-p representa a probabilidade de se obter para
o estatístico critério do teste um valor mais extremo (≤
ou ≥) que o valor calculado com os dados da amostra,
sob a condição de H0 ser verdadeira.
Representa o menor valor de probabilidade para o qual
H0 pode ser rejeitada.
O valor-p pode ser usado para tomar a decisão
Se valor-p ≥ α, não se rejeita H0
Se valor-p < α, rejeita-se H0
Exemplo Ilustrativo: A Distribuição de Probabilidades
A variável aleatória (X) que representa o consumo de O2 por
parte das suspensões celulares pode ser assumida como tendo
distribuição normal, N (X; µ ≅13,43 ml, σ2≅1,644 ml2).
Se a amostra fosse de tamanho elevado (n≥30), a população
das médias teria, por força do teorema do limite central,
distribuição normal, e poderíamos então usar a Tabela da Lei
Normal Padrão. Para efeito de tomada de decisão sobre as duas
hipóteses em causa (H0 e H1), calcularíamos então:
X−µ
_
zamostra =
s
0
n
Como, porém a amostra é de pequeno tamanho (n=15),
vamos ter de utilizar a distribuição t de Student com graus de
liberdade=15-1=14. Para efeito de tomada de decisão sobre as
duas hipóteses em causa (H0 e H1), calculamos então:
X−µ
_
t amostra =
s
0
n
6
Exemplo Ilustrativo: Cálculo do valor amostral do estatístico
Substituindo Média=13,43 ml, µ0=12 ml,
s2=1,644 ml2 e n=15 pessoas, o valor do
estatístico t calculado a partir da
amostra vem dado por:
X−µ
=
_
t
amostra
s
n
0
=
13 , 43 − 12
1, 43
=
≅ 4 ,319
0 ,33106
1,644
15
Exemplo Ilustrativo: Nível de Significância e Região de Rejeição
Se a margem de erro pretendida para a inferência é de 5%, então o nível
de significância do teste é α = 0,05.
O teste da hipótese nula é, neste caso, unilateral, porque a hipótese nula
especifica um sentido para a diferença (“maior que”): H1: µ > 12 ml.
Assim sendo, a probabilidade representada pelo nível de significância
(0,05) é considerada totalmente na extremidade direita da Distribuição t de
Student com 14 graus de liberdade, para efeitos de definição da região de
rejeição do teste.
Para encontrar o valor crítico do teste - que separa a zona de rejeição da
zona de não rejeição - procura-se no corpo da tabela da Distribuição t de
Student com 14 graus de liberdade o valor de t que corresponde à
probabilidade de 0,05 (lida na linha inferior da tabela).
Nestes termos, o valor crítico do teste é t0,05 (14)= 1,761.
7
Exemplo Ilustrativo: Nível de Significância e Região de Rejeição
Tabela do t de Student
1. O valor de t(14) a que
corresponde a probabilidade α =
0,05 é t=1,761.
A área sob a curva da distribuição t
de Student com gl=14, situada para
a direita de 1,761 é igual a 0,05.
Exemplo Ilustrativo: Nível de Significância e Região de Rejeição
α = 0,05
t(14)
-2
Região de Não
Rejeição de H0
tamostra < 1,761
-1
0
1 1,761 2
Região de
Rejeição de H0
tamostra ≥ 1,761
8
Exemplo Ilustrativo: Tomar a Decisão sobre H0 (1º processo)
α = 0,05
tamostra = 4,319 t(14)
-2
-1
0
11,761
2
Como tamostra se localiza na
região de rejeição, rejeitamos
H0.
Exemplo Ilustrativo: Tomar a Decisão sobre H0 (2º processo)
α = 0,05
p < 0,05
4,319
-2
-1
1.
2.
0
1 1,761 2
z
Como tamostra=4,319 se situa à esquerda do valor crítico
t0,05=1,761, a probabilidade associada a tamostra é inferior a
0,05.
Rejeitamos H0 porque a probabilidade associada ao valor
amostral de t é inferor ao nível de significância do teste
(0,05).
9
Exemplo Ilustrativo: Tirar uma Conclusão do Âmbito da Pesquisa
A conclusão que se tira do teste de hipóteses
deve ser sempre formulada no contexto do
problema de pesquisa que está a ser estudado.
No exemplo ilustrativo, conclui-se que há
evidência nos dados recolhidos para se
acreditar (com uma margem de erro de 5%)
que o consumo médio de oxigénio da
população de suspensões celulares excede 12
ml.
Conformidade de uma média com um valor
H0: µ = 12
H1: µ > 12
α = 0,05
n = 15
Região de Rejeição:
Rejeitar
RejectH0
0,05
.05
0 1.645
1,761
Zt(14)
Valor amostral do estatístico:
t
amostra
amostra
==
X
X −− µ 00 13
13,,43
43 −− 12
12
==
== 44,,319
319
ss
11,,644
644
nn
15
15
Decisão:
Rejeitar H0 a α = 0,05
Conclusão:
Há evidência para concluir que
o consumo de O2 excede 12 ml.
10
Marcha Geral de um Teste de Hipóteses
Formular as hipóteses nula
(H0) e alternativa (H1)
Escolher o teste e a distribuição de
probabilidades adequados (normal, t, F, χ2…)
Adoptar o nível de
significância (α)
Calcular o valor amostral
do estatístico do teste
Determinar a probabilidade
associada ao valor amostral (p)
Comparar com o nível
de significância, α
Determinar o valor crítico do teste e
estabelecer a região de rejeição de H0
Determinar se o valor amostral do estatístico
se situa na região de rejeiçao de H0
Marcha Geral de um Teste de Hipóteses
Comparar com o nível
de significância, α
Sim
Rejeitar H0
p<α?
Determinar se o valor amostral do estatístico
pertence à região de rejeição de H0
Não
Sim
Não rejeitar H0
Rejeitar H0
Pertence ?
Não
Não rejeitar H0
Tirar Conclusões no Âmbito da Área de Pesquisa
11
Testes de Hipóteses com Médias
1.Conformidade de uma média com um
valor.
2.Comparação de duas médias
(amostras independentes; variâncias
iguais).
3.Comparação de duas médias
(amostras independentes; variâncias
diferentes).
4.Comparação de duas médias
(amostras associadas).
Conformidade de uma média com um valor
Mediram-se os consumos de oxigénio (em ml)
durante a incubação de uma amostra aleatória de 15
suspensões celulares.
A partir dos dados obtidos, calculou-se média=13.43
ml e variância=1.644 ml2.
O investigador pretende-se averiguar se os dados
fornecem evidência suficiente para se concluir, ao nível
de 5%, que a média dos consumos de O2 da população
de suspensões celulares excede 12 ml.
Questão: Há evidência na informação colhida na
amostra para se concluir, com uma margem de erro de
5%, que os consumos de oxigénio na população de
suspensões celulares excede 12 ml?
12
Conformidade de uma média com um valor
H0: µ = 12
H1: µ > 12
α = 0,05
n = 15
Região de Rejeição:
Rejeitar
RejectH0
0,05
.05
0 1.645
1,761
Zt(14)
Valor amostral do estatístico:
t
amostra
amostra
==
X
X −− µ 00 13
13,,43
43 −− 12
12
==
== 44,,319
319
ss
11,,644
644
nn
15
15
Decisão:
Rejeitar H0 a α = 0,05
Conclusão:
Há evidência para concluir que
o consumo de O2 excede 12 ml.
Comparação de duas médias: amostras independentes, variâncias iguais
Quantificou-se a citocromo-oxidase (mm3/10 min./mg) em baratas
do sexo masculino do género Periplaneta de dois grupos
experimentais, um grupo controlo (n=12), e um grupo a que se
injectou metoxicloro 24 horas antes da quantificação (n=10).
Controlo
Tratado
18.1 20.3 19.4 21.6 18.9 19.0 18.5 21.6 22.1 19.5 18.7 18.7
23.9 25.6 24.8 22.9 26.1 25.0 23.7 24.5 24.9 26.6
O objectivo deste estudo era averiguar se a droga acentua a
actividade da enzima.
Questão: Há suficiente evidência nestes resultados para se concluir,
ao nível de 5%, que o metoxicloro acentua a actividade da enzima
citocromo-oxidase nas baratas?
13
Comparação de duas médias: amostras independentes, variâncias iguais
H0: µ1 = µ2 (µµ =controlo; µ =tratado)
H1: µ1 < µ2
α = 0,05
t
gl = 12 + 10 - 2 = 20
Região de Rejeição:
1
2
Valor amostral do estatístico:
__
==
amostra
amostra
__
X 11 −− X 22
22
pp
s
 1
1 
⋅⋅ 1 ++ 1 
 n11 n22 
19
19,,77 −− 24
24,,88
== −−99,,425
425
11 11 


11,,597
597⋅⋅ ++ 
 12
12 10
10 
==
Decisão:
Rejeitar H0 a α = 0,05
Rejeitar
RejectH0
Conclusão:
Há evidência para se concluir que o
metoxicloro acentua a actividade da
enzima.
.05
t
-1.729
-1,725 0
• s2maior/s2menor = 1,873/1,260= 1,5
• sendo esta razão < 3, assume-se que as
variâncias são homogéneas, e usa-se a
variância ponderada (s2p):
(n1 − 1). s 1 + (n2 − 1). s
2
2
s
p
=
2
n1 + n 2 − 2
2
=
(12 − 1).1,873 + (10 − 1).1,260
= 1,597
12 + 10 − 2
Comparação de duas médias: amostras independentes, variâncias diferentes
O estrôncio 90 (90S) é um elemento radioactivo produzido nas explosões nucleares, e
que aparece associado ao cálcio no organismo humano.
Em zonas de produção leiteira, 90S pode contaminar o leite por via das pastagens
ingeridas pelas vacas, e vir mais tarde a concentrar-se nos ossos das pessoas que o
bebem.
Fez-se um estudo para comparar o teor médio de 90S nos ossos de crianças e de
pessoas adultas, na presunção de que deveria ser superior nas primeiras do que nas
segundas, visto que o elemento começa nelas a acumular-se logo nos primeiros anos de
desenvolvimento do esqueleto.
A partir das amostras, calculou-se:
n
Média
Variância
Crianças
121
2,6 pC g-1
1,44
Adultos
61
0,4 pC g-1
0,0121
Questão: É legítimo concluir, com uma margem de erro de 5%,
que o teor médio de 90S é superior no esqueleto das crianças do que
no dos adultos?
14
Comparação de duas médias: amostras independentes, variâncias diferentes
H0: µ1 = µ2 (µ =crianças; µ =adultos)
H1: µ1 > µ2
α = 0,05
gl´ ≈ 123
Região de Rejeição:
1
2
Valor amostral do estatístico:
__
==
t'amostra
amostra
__
X 11 −− X 22 =
=
s ++ s
n n
22
11
22
22
11
22
22,,66−−00,,44
== 20
20
11,,44
44 + 00,,0121
0121
+
121
61
121
61
Decisão:
Rejeitar
H0
Reject
Rejeitar H0 a α = 0,05
Conclusão:
Há evidência para se concluir que a acumulação
de 90S é mais elevada no esqueleto das
crianças.
.05
• s2maior/s2menor = 1,44/0,0121= 119
• sendo esta razão >> 3, assume-se que as variâncias não são
0 1,658
1.833
t
homogéneas, não fazendo sentido usar a variância ponderada
(s2p)
• trabalha-se com número de graus de liberdade ajustado (gl’):
2
gl' =
2
 s2 1

2

+ s 2 

n1
n2  = 1,44 121 + 0 ,0121 61 ≅ 123

2
2
2
0 ,0121 2
1,44
 s2 1   s2 2 

 

121 +
61

n1  +  n2 
121 − 1
61 − 1

n1 − 1
n2 − 1
(
(
) (
)
)
Comparação de duas médias: amostras associadas (emparelhadas)
Nos testes atrás estudados, as amostras eram amostras
independentes (os dados de uma das amostras não
estavam por qualquer forma associados aos dados da
outra amostra).
Há todavia certos estudos em que cada observação da
1ª amostra está de um certo modo correlacionada com
uma observação da 2ª amostra, de tal forma que
podemos dizer que os dados ocorrem aos pares
(amostras emparelhadas)
15
Comparação de duas médias: amostras associadas (emparelhadas)
1. Sobre um mesmo indivíduo são recolhidos dois
dados, um concernente a cada tratamento a
comparar:
comparar dois métodos de análise para uma mesma
substância;
estudar os efeitos de uma droga sobre uma função
fisiológica animal, em que cada indivíduo é observado
“antes” e “depois” da respectiva administração;
estudar a evolução de uma característica biométrica entre
duas idades num grupo de organismos, em que cada
indivíduo é medido ao iniciar-se o estudo, e ao atingir a
segunda idade considerada;
comparar a potência de dois antigéneos, em que cada um
deles é injectado num dos braços de cada indivíduo, e se
medem depois os diâmetros das zonas eritematosas que
se formam etc.
Comparação de duas médias: amostras associadas (emparelhadas)
2. Sobre dois indivíduos distintos mas considerados
como idênticos no essencial, são obtidos os
dados necessários à comparação dos dois
tratamentos:
comparar os efeitos de duas rações sobre a engorda de
animais, em que se dispõe de pares de animais da mesma
ninhada e iguais sexo e peso, e se administra a cada
membro de um par um dos tipos de ração;
ensaios em dois cultivares de uma espécie são instalados
em parcelas de terreno vizinhas (con solo idêntico e sob
idênticas condições gerais), a fim de controlar os efeitos
do ambiente sobre o seu rendimento.
16
Comparação de duas médias: amostras associadas (emparelhadas)
Uma comparação emparelhada assenta em duas
amostras que não são independentes uma da
outra, visto que há uma correspondência estreita
(uma associação) termo a termo, entre as
observações de cada uma delas.
Por esse motivo, a análise estatística dos
resultados deve ser feita sobre a amostra das
diferenças de observações do mesmo par, e não
mediante a consideração de duas amostras
independentes, como se tem feito até aqui.
Comparação de duas médias: amostras associadas (emparelhadas)
Fez-se um estudo para testar a eficácia de uma certa droga sobre a pressão intra-ocular,
no decurso do qual esta variável foi medida (mm de Hg) em 12 indivíduos idosos, antes
e depois da administração do medicamento:
Indivíduo
Antes
Depois
Diferença
1
21.6
14.5
7.1
2
18.8
12.9
5.9
3
22.2
14.0
8.2
4
22.2
16.1
6.1
5
18.7
12.0
6.7
6
27.0
17.5
9.5
7
19.5
14.1
5.4
8
20.7
12.9
7.8
9
25.0
17.9
7.1
10
18.9
12.0
6.9
11
23.4
16.4
7.0
12
29.3
24.2
5.1
Pretende-se testar a hipótese segundo a qual a administração da droga é responsável
por um decréscimo da pressão intraocular superior a 5 mm de Hg, ao nível de
significância de 5%.
Questão: Pode-se concluir, com uma segurança de 95%, que a droga reduz
em mais de 5 mm de Hg a pressão intra-ocular?
17
Comparação de duas médias: amostras associadas (emparelhadas)
H0: µD = 5 (µ = média das diferenças)
H1: µD > 5
α = 0,05
gl = 12 – 1 = 11
Região de Rejeição:
D
Rejeitar
H0
Reject
Valor amostral do estatístico:
t
amostra
=
µ −µ
D
2
s
n
D
D
0
=
6 ,9 − 5
= 5,370
1,502
12
Decisão:
Rejeitar H0 a α = 0,05
.05
Conclusão:
0 1,796
1.833
t
Há evidência para se concluir que
a droga é responsável, em média,
por reduções da pressão intraocular superiores a 5 mm de Hg.
Premissas da aplicabilidade dos testes relativos a médias
As populações amostradas devem ter
distribuição normal.
As amostras seleccionadas devem ser
aleatórias.
Os métodos permanecem válidos se a
distribuição das populações se não afastar
muito da normal, isto é, se elas forem pelo
menos simétricas, unimodais e de variância
não exageradamente elevada. Nestes casos, os
eventuais afastamentos da normalidade
podem ser compensados mediante a utilização
de amostras de maior tamanho.
18