Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 28 – O CAMPO ELÉTRICO
26. A que distância, ao longo do eixo de um anel carregado de raio R, a intensidade do campo
elétrico axial é máxima?
(Pág. 29)
Solução.
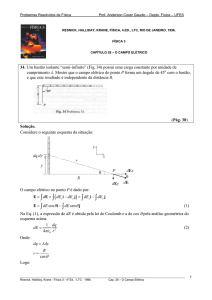
Considere o seguinte esquema da situação:
Rdφ
+ + ++
dM
+
+
+
+
dφ R
+
dEz dEx
θ
+
+
x
+
dE
dEy
+
y
+
+
+
+
+ + +
+
z
O campo elétrico no ponto é dado por:
x
E = ∫ dE = ∫ ( dEx i + dE y j + dEz k ) = ∫ dEx i + ∫ dE y j + ∫ dEz k
A simetria envolvida na situação mostra que as integrais em j e k são nulas.
=
E
∫ dE i + 0 +=0 ∫ dE cos θ i
x
(1)
Na Eq. (1), a expressão de dE é obtida pela lei de Coulomb e a de cos θ pela análise do esquema
acima.
1
dq
dE =
4πε 0 ( R 2 + x 2 )2
cos θ =
x
(R
2
+ x2 )
1/ 2
Logo:
E=∫
1
xdq
4πε 0 ( R 2 + x 2 )3 / 2
i
(2)
A expressão de dq é obtida por meio da densidade linear de carga do anel λ.
q
dq
=
λ =
2π R Rd φ
dq =
q
dφ
2π
(3)
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Substituindo-se (3) em (2):
1 q
x
dφ i
E=∫
2
4πε 0 2π ( R + x 2 )3 / 2
Na expressão acima, somente φ é variável. Portanto, tudo o mais pode ser retirado de dentro da
integral.
2π
1 q
x
1 q
x
dφ i
2π i
E =
3
/
2
∫
0
4πε 0 2π ( R 2 + x 2 )
4πε 0 2π ( R 2 + x 2 )3 / 2
E=
1
qx
4πε 0 ( R 2 + x 2 )3 / 2
(4)
i
A Eq. (4) corresponde ao campo elétrico sobre o eixo do anel, a uma distância x do seu centro. O
valor de E é zero para x = 0 e também é zero para x = +∞. Como E é positivo nesse intervalo, tornase evidente que há um valor máximo que E atinge em algum lugar para 0 < x < +∞. Para achar o
valor de x que torna máximo o de E, módulo de E, basta calcular o valor de x que torna zero a
derivada de E em relação à x.
2 3/ 2
2
2
2 1/ 2 
 2
1  ( R + x ) − 3x ( R + x ) 
=
0
2
2 3

4πε 0 
R
x
+
(
)


A expressão central será zero somente se:
dE
dx
(R
2
+ x2 )
3/ 2
− 3x 2 ( R 2 + x 2 )
1/ 2
=
0
R2 + x2 =
3x 2
x=
R
2
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
2