ELC1031 - L2.2

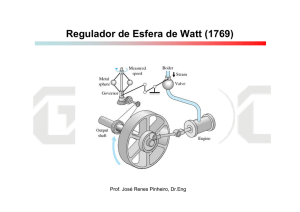
Modelos Matematicos de Sistemas
Introdução;
Equações Diferenciais de Sistemas Físicos;
Aproximações Lineares de Sistemas Físicos;
Transformada de Laplace;
Função de Transferência de Sistemas Lineares;
Modelos em Diagrama de Blocos;
Modelos em Diagramas de Fluxo de Sinais;
Analise Computacional de Sistemas de Controle;
Exemplo de Projetos.
Prof. José Renes Pinheiro, Dr.Eng
1
Equações Diferenciais de Sistemas Físicos
As Equações Diferenciais que descrevem o desempenho de um
sistema dinâmico de um sistema físico são obtidas utilizando-se
as Leis físicas do processo.
Ta (t ) − Ts (t ) = 0
Variável-Através
w(t ) = ws (t ) − wa (t )
Variável-Sobre
(a) Sistema de Torção Massa-Mola
(b) Elemento Mola
Prof. José Renes Pinheiro, Dr.Eng
2
Resumo das Variáveis Através e Sobre para Sistemas Físicos
Sistema
Variável de
Elemento Através
Variável Através
Integrada
Variável de
Elemento Sobre
Variável Através
Integrada
Elétrico
Corrente i
Carga q
Diferença de
Tensão v21
Enlace de Fluxo
821
Mecânico em
Translação
Força F
Quantidade de
Movimento P
Diferença de
velocidade v21
Diferença de
deslocamento y21
Mecânico em
Rotação
Torque T
Momento cinético h
Diferença de
velocidade angular
T21
Diferença de
deslocamento
angular 221
Momento de
Pressão (21
Fluido
Vazão Volumétrica
Q
Volume V
Diferença de
Pressão P21
Térmico
Fluxo Térmico q
Energia Térmica H
Diferença de
Temperatura T21
Prof. José Renes Pinheiro, Dr.Eng
3
Sistema Massa-Mola-Amortecedor
(a) Sistema MassaMola-Amortecedor
(b) Diagrama
Corpo Livre
2
d y (t )
dy (t )
M
+b
+ ky (t ) = r (t )
2
dt
dt
Prof. José Renes Pinheiro, Dr.Eng
4
Circuito RLC
t
v(t )
dv(t ) 1
+C
+ ∫ v(t )dt = r (t )
R
dT
L0
Prof. José Renes Pinheiro, Dr.Eng
5
Solução da Equação Diferencial
Métodos Clássicos:
1. Fatores de Integração
2. Método dos coeficientes a determinar
3. Transformada de Laplace
y (t ) = K1e −α1t sen( β1t + θ1 )
v(t ) = K 2 e −α 2t sen( β 2t + θ 2 )
Prof. José Renes Pinheiro, Dr.Eng
6
Aproximações Lineares de Sistemas Físicos
Os modelos mais precisos de sistemas físicos são não-lineares.
A Transformada de Laplace não pode ser utilizada na solução de
equações diferenciais não-lineares.
Técnica de Linearização de sistemas não-lineares
Prof. José Renes Pinheiro, Dr.Eng
7
Modelo Oscilador Tipo Pendulo
L → comprimento do pêndulo;
M → massa do pêndulo;
f → força que atua no pêndulo;
g → gravidade.
A equação diferencial que descreve o movimento do pêndulo
L d 2 θ( t )
.
= − sen θ( t )
2
g dt
Prof. José Renes Pinheiro, Dr.Eng
8
Série de Taylor
df
f (θ) = f (θ0 ) +
dθ
d2f
.(θ − θ0 ) + 2
( θ= θ0 )
dθ
(θ − θ0 ) 2
.
+......
( θ=θ0 )
2!
Se a variação “q - θ0” é pequena, os termos de maior grau podem ser desprezados
na série de Taylor. Isto resulta em:
df
f ( θ) ≅ f ( θ 0 ) +
f(θ) = sen θ
dθ
( θ = θ0 )
. (θ − θ 0 )
, e:
sen θ = sen θ0 + { cos θ0 }.( θ − θ0 )
Como, o pêndulo mostrado, opera na região em que , pode-se
linearizar a função em torno do ponto .
sen θ ≅ 0 + 1. ( θ − 0 0 ) ∴
senθ ≅ θ
Prof. José Renes Pinheiro, Dr.Eng
L d 2 θ( t )
.
= −θ( t )
2
g dt
9
Transformada de Laplace
Prof. José Renes Pinheiro, Dr.Eng
10
FUNÇÃO DE TRANSFERÊNCIA
A FTLTIde
um Time
LTIInvariant
é definida
como
sendo
a relação
– Linear
- Sistema Linear
Invariante
no Tempo
entre
de d Laplace
saída
d y(t ) asd Transformadas
y(t )
dy(t )
x(t )
d x(tda
)
dx(t ) e da
a
+a
... + a
+ a . y(t ) = b
+b
... + b
+ b .x(t )
dt
dt
dt
dt
dt
entrada,
com
todasdt as condições
iniciais
nulas.
n−1
n
0
n
1
n−1
m−1
m
n−1
n
0
m
1
m−1
m−1
m
Onde: n≥m
x(t) ⇒ entrada (função excitação) e y(t) ⇒ saída (função resposta)
Aplicando-se a transformação de laplace, temos:
(a
0
.S n + a 1S n − 1 + ....+ a n − 1 .S + a n ) Y ( s ) = ( b 0 .S m + b 1 .S m − 1 + ....+ b m − 1 .S + b m ) X ( s )
b 0 . S m + b1 . S m − 1 + .... + b m − 1 . S + b m
Y (s)
G (s) =
=
X (s)
a 0 . S n + a 1 . S n − 1 + .... + a n − 1 . S + a n
Prof. José Renes Pinheiro, Dr.Eng
Função de
Transferência
Sistema de ordem n
11
COMENTÁRIOS SOBRE FUNÇÃO DE
TRANSFERÊNCIA
A FT de um sistema é uma propriedade que independende da
natureza e da magnitude da entrada;
Possibilitar um sistema dinâmico ser representado por
expressões algébricas da variável complexa “S”;
A FT não fornece informações a respeito da estrutura física do
sistema. A FT de sistemas fisicamente diferentes podem ser
idênticas;
Se a FT de um sistema é conhecida, a resposta do mesmo pode
ser analisada para diferentes formas de excitação (entrada), com a
finalidade de compreender a natureza e o comportamento do
sistema;
Se a FT pode ser obtida experimentalmente pela introdução de
sinais de entrada conhecidos e estudando-se as respostas obtidas.
A FT fornece uma descrição completa das características
dinâmicas do sistema.
Prof. José Renes Pinheiro, Dr.Eng
12