Numeros Complexos

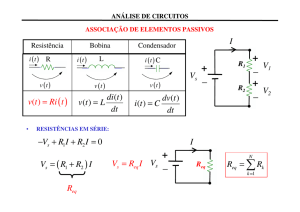
Exercícios de Revisão: Análise Complexa 1- Números Complexos
Exercícios Propostos Globais I .............................................................................................. 1
Soluções dos Exercícios Propostos Globais I ........................................................................ 2
1 Introdução ........................................................................................................................... 4
2 Definições e propriedades elementares .............................................................................. 4
2.1 Números Complexos ....................................................................................................... 4
2.2 Propriedades elementares .............................................................................................. 5
2.3 O conjugado................................................................................................................... 5
2.4 Módulo de um número complexo................................................................................... 6
2.5 Argumento de um número complexo............................................................................... 7
2.6 Potência de um número complexo ................................................................................. 7
2.7 Exercícios Resolvidos ..................................................................................................... 8
3 Equações e Inequações ...................................................................................................... 10
3.1 Equações ....................................................................................................................... 10
3.2. Exercícios Resolvidos .................................................................................................. 10
3.3. Exercícios Propostos ................................................................................................... 10
3.4. Soluções/Sugestões dos Exercícios Propostos............................................................. 11
4 Parametrizações de curvas................................................................................................ 12
4.1- Descrição paramétrica em IR2 .................................................................................... 12
4.2 Descrição paramétrica em ^ ....................................................................................... 12
4.3. Exercícios Propostos ................................................................................................... 13
5 Representação no plano complexo ................................................................................ 14
Descrição: Esta ficha de exercícios de revisão é uma compilação de enunciados com
solução/resolução. Para iniciar a resolução de exercícios é absolutamente necessário que o
aluno tenha a teoria bem estudada. Agradece-se a indicação de gralhas e/ou inconsistências:
[email protected].
Introdução à análise complexa I
Exercícios Propostos Globais I
EPGI.1. Determine o lugar geométrico das imagens dos complexos z que satisfazem:
a) z − i = z + i
b) arg (z - a ) = θ a, θ fixos
c) 1 < z − 4 < 2
d)
z−a
=λ
z−b
1
Introdução à análise complexa I
Soluções dos Exercícios Propostos Globais I
EPGI.1.
a) Recta y = 0
y
i
y=0
x
-i
b) Semi-recta com origem em a e declive tg(θ)
a ∈ 1º
y
θ
a
x
c) 1 < (x − 4) + y 2 < 4 - coroa circular aberta com r = 1, R = 2 e C = 4
2
y
4
x
2
Introdução à análise complexa I
d) Se λ = 1
Æ mediatriz do segmento de recta que une os pontos a e b
y
a, b ∈ 1º quadrante
b
a
x
Se λ ≠ 1
Æ circunferência com centro z 0 =
λ b−a
a − λ2 b
e
raio
r
=
1 − λ2
1 − λ2
y
z0
z0 ∈ 1º quadrante
r
x
3
Introdução à análise complexa I
1 Introdução
Descrever a necessidade histórica dos números complexos, não para a resolução de equações
do 2º grau, mas para dar sentido à fórmula resolvente de equações do 3º grau.(...).
2 Definições e propriedades elementares
2.1 Números Complexos
Representação algébrica, rectangular ou cartesiana1:
z = x + yi ; x, y ∈ R
Representação trigonométrica ou polar:
z = ρ cis (θ )
Em que :
Parte imaginária de z :
Parte real de z
x = ρ sin θ ≡ Im(z )
y = ρ cos θ ≡ Re( z )
Exemplo
Passe o número complexo z = 8i para a forma trigonométrica.
z = 02 + 82 = 64 = 8
a 0
⎫
= =0 ⎪
z 8
π
⎪
⎬ θ=
b 8
2
sen(θ ) = = = 1 ⎪
⎪⎭
z 8
Passando para a forma trigonométrica:
cos(θ ) =
z = z .(cos(θ ) + i.sen(θ ))
⎛
⎛π ⎞
⎛ π ⎞⎞
z = 8. ⎜ cos ⎜ ⎟ + i.sen ⎜ ⎟ ⎟
⎝2⎠
⎝ 2 ⎠⎠
⎝
Observação: cisθ é apenas uma forma “condensada” de escrever cos θ + i sin θ .
Definição: Unidade imaginária: i , em que i 2 ≡ −1 .
1
Ou z = a + bi ; a,b
∈3.
4
Introdução à análise complexa I
⎧ 1 , n = 4k
⎪ i , n = 4k + 1
⎪
Exemplo: i n = ⎨
, com k∈IN.
−
i
,
n
=
4
k
+
2
⎪
⎪⎩− 1, n = 4k + 3
2.2 Propriedades elementares
Definição: Sejam z = a + bi e ω = c + di , então:
i.
ii.
iii.
iv.
z + ω = (a + c) + (b + d)i
z − ω = (a − c) + (b − d)i
z × ω = (a + bi).(c + di) = (ac − bd) + (bc + ad)i
z
1
[(ac + bd ) + (bc − ad )i]
= 2
ω c + d2
Na realidade ii. e iv. são casos particulares de i. e iii., respectivamente.
Proposição: Sejam z1 = ρ 1 cisθ 1 e z 2 = ρ 2 cisθ 2 então
i.
z1 × z 2 = ρ 1 ρ 2 cis (θ 1 + θ 2 )
ii.
z 2−1 =
iii.
z1 ρ 1
=
cis(θ 1 − θ 2 ) , z 2 ≠ 0
z2 ρ 2
⎛ 1
cis⎜⎜
ρ2 ⎝θ2
1
⎞
⎟⎟ , z 2 ≠ 0
⎠
2.3 O conjugado
Definição:
“Seja z = a + bi define-se complexo conjugado de z por z = a − bi 2.”
Propriedades:
i.
z=z
ii.
z + z = 2 Re(z )
iii.
z − z = 2 Im( z )
iv.
z = z ⇔ z∈\
2
ou conj(z).
5
Introdução à análise complexa I
2.4 Módulo de um número complexo
Definição: Módulo, norma ou valor absoluto
“Seja z = a + bi define-se módulo de z pelo real positivo z = x 2 + y 2 .”
Propriedades:
i.
z1 × z 2 = z1 × z 2
ii.
z
z1
= 1 , z2 ≠ 0
z2
z2
iii.
z1 + z 2 ≤ z1 + z 2 (desigualdade triangular).
Exemplo: Cálculo do Módulo de um Número Complexo
(4 − 3i )(12 − 5i )
.
2i
Primeiramente colocamos o número na forma x + yi :
Determine o módulo do número complexo
(4 − 3i )(12 − 5i ) (− 2i )
.
( 2i )
(− 2i )
=
(48 − 20i − 36i + 15i 2 ).(− 2i )
−2i 2
=
(33 − 56i ).(− 2i )
=
−2(−1)
−33 2i − 56 2
33 2
i
= − 28 2 −
2
2
Agora encontramos o módulo desse número complexo:
=
2
⎛ 33 2 ⎞
2178
8450
4225
z = a + b = (−28 2) + ⎜⎜ −
=
=
=
⎟⎟ = 1568 +
2
4
4
2
⎝
⎠
2
=
2
65 2 65 2
.
=
2
2 2
2
→
z =
65 2
2
6
Introdução à análise complexa I
2.5 Argumento de um número complexo
Argumento
: arg z = θ + 2kπ , k∈IN
“
principal
: arg z ∈ [- π ,+ π [
“
positivo mínimo : arg z ∈ [0, 2 π [
Exemplo: Obtenha o argumento do numero complexo: 2 + i2 3
z = 2 + 2 3i
→
z = 22 + (2 3) 2 = 4 + 12 = 16 = 4
⎫
⎪
π
⎪
0
⎬ θ = 60 =
3
3 ⎪
b 2 3
=
sen(θ ) = =
4
2 ⎪⎭
z
cos(θ ) =
a 2 1
= =
z 4 2
Exemplo: Obtenha na forma trigonométrica do numero complexo: 8i
É determinado obtendo separadamente do módulo e do argumento do número
complexo dado na forma algébrica:
z = 02 + 82 = 64 = 8
a 0
⎫
= =0 ⎪
z 8
π
⎪
⎬ θ=
b 8
2
sen(θ ) = = = 1 ⎪
⎪⎭
z 8
Passando para a forma trigonométrica:
cos(θ ) =
z = z .(cos(θ ) + i.sen(θ ))
⎛
⎛π ⎞
⎛ π ⎞⎞
z = 8. ⎜ cos ⎜ ⎟ + i.sen ⎜ ⎟ ⎟
⎝2⎠
⎝ 2 ⎠⎠
⎝
2.6 Potência de um número complexo
Proposição: 1ª Fórmula de De Moivre- Potenciação
“Seja z = ρ cisθ , então z n = ρ n .cis(nθ ) , n ∈IN.”
Proposição: 2ª Fórmula de De Moivre- Radiciação
⎛ θ + 2kπ ⎞
“Seja z = ρ cisθ , então n z = n ρcis⎜
⎟, k=0,...,n-1”
⎝ n ⎠
7
Introdução à análise complexa I
Observação: esta fórmula tem uma interpretação geométrica: todas as raízes
estão sobre a mesma circunferência de raio n ρ , cuja distância angular constante é
2π / n ; i.e., as raízes definem um polígono regular incrito numa circunferência de
raio n ρ .
Exemplos:
⎛ 2kπ ⎞
1 = cis⎜
⎟ , k=0,...,n-1;
⎝ n ⎠
ii. 3 1 = 1 , − 1 / 2 + i 3 / 2, − 1 / 2 − i 3 / 2 ;
i.
iii.
n
4
1 = 1 , i, -1, -i.
2.7 Exercícios Resolvidos
ER2.7.1 Calcule
2+i
.
5 − 3i
Res.:Multiplicam-se ambos os termos da fração pelo número complexo conjugado do
denominador:
(2 + i ) (5 + 3i ) 10 + 6i + 5i + 3i 2 10 + 11i − 3 7 + 11i 7 11
.
=
=
=
=
+ i
(5 − 3i ) (5 + 3i )
25 − 9i 2
25 − (−9)
34
34 34
ER2.7.2 Coloque na forma a + bi a expressão
1− i
i
+
.
1+ i i − 2
Res.:Em cada fração, multiplicamos seus termos pelo número complexo conjugado do
denominador:
(1 − i ) (1 − i )
i
( −2 − i )
.
+
.
(1 + i ) (1 − i ) (−2 + i ) (−2 − i )
1 − 2i
−2i 1 − 2i
+
= −i +
=
2
5
5
=
=
1 − 2i + i 2 −2i − i 2
+
=
1− i2
4 − i2
−5i + 1 − 2i
1 − 7i
=
5
5
1 − 2i − 1 −2i − (−1)
+
=
1 − (−1)
4 − (−1)
1 7
=
− i
5 5
8
Introdução à análise complexa I
ER2.7.3 Calcule:
92
4
a) i
92
→
92
23
→ i =1
0
b) i
45
→
45
4
44
11
0
1
310
c) i
310
→
→ i1 = i
4
308
77
→ i = −1
2
d) i
1081
→
1081
4
1080
270
2
→ i1 = i
1
e) i 4 n = i 4 = i 2 .i 2 = (−1).(−1) = 1
f) i 4 n +1 = i 4 n .i = 1.i = i
g) i 4 n + 2 = i 4 n .i 2 = 1.(−1) = −1
⎛
⎛π ⎞
⎛ π ⎞⎞
ER2.7.4 Dados z1 = 5(cos(π ) + i.sen(π )) e z2 = 3. ⎜ cos ⎜ ⎟ + i.sen ⎜ ⎟ ⎟ , obtenha z1 .z2 .
⎝3⎠
⎝ 3 ⎠⎠
⎝
Re s.: z1 = (5cos(π )) 2 + (5sen(π )) 2 = (−5) 2 + 02 = 25 = 5
⎛
9 27
36
⎛ π ⎞⎞ ⎛
⎛ π ⎞⎞
z2 = ⎜ 3cos ⎜ ⎟ ⎟ + ⎜ 3sen ⎜ ⎟ ⎟ =
+
=
= 9 =3
4 4
4
⎝ 3 ⎠⎠ ⎝
⎝ 3 ⎠⎠
⎝
2
2
a −5
⎫
cos(θ1 ) =
=
= −1⎪
5
z1
⎪
⎬ θ1 = π
b 0
sen(θ1 ) =
= =0 ⎪
⎪⎭
z1 5
cos(θ 2 ) =
a 3/ 2 1
=
=
3
2
z2
3 3
b
3
sen(θ 2 ) =
= 2 =
z2
3
2
⎫
⎪
⎪⎪
π
⎬ θ2 =
3
⎪
⎪
⎪⎭
z1 .z2 = z1 . z2 .(cos(θ1 + θ 2 ) + i.sen(θ1 + θ 2 ))
⎛
π⎞
π ⎞⎞
⎛
⎛
z1 .z2 = 5.3. ⎜ cos ⎜ π + ⎟ + i.sen ⎜ π + ⎟ ⎟
3⎠
3 ⎠⎠
⎝
⎝
⎝
⎛
⎛ 4π
z1 .z2 = 15. ⎜ cos ⎜
⎝ 3
⎝
⎞
⎛ 4π ⎞ ⎞
⎟ + i.sen ⎜
⎟⎟
⎠
⎝ 3 ⎠⎠
9
Introdução à análise complexa I
3 Equações e Inequações
3.1 Equações
Toda a equação redutível à forma az n + b = 0 , onde a, b ∈ C , a ≠ 0, n ∈ ` é fácil de
resolver, basta isolar zn e aplicar a definição de radiciação em ^ .
az n + b = 0 ⇔ z n = −
b
b
⇔z=n −
a
a
e obtemos n raizes distintas.
3.2. Exercícios Resolvidos
ER3.1 Considere a seguinte equação: z 2 − 1 − i = 0 .
i. resolva-a em ^ .
ii. represente as duas soluções e comente a afimação: “São complexos conjugados”.
Resolução:
z 2 −1− i = 0 ⇔ z = 1+ i =
2 e iπ / 4 =
⎡⎛ π / 4 + 2kπ ⎞ ⎤
2 exp ⎢⎜
⎟i ⎥ , com k=0,1.
2
⎠⎦
⎣⎝
9π
π
i
i
⎧
⎫
O conjunto solução é S = ⎨4 2e 8 , 4 2e 8 ⎬ e os complexos não são complexos conjugados.
⎩
⎭
3.3. Exercícios Propostos
EP3.1 Comente a seguinte afirmação, justificando adequadamente: “Se um número complexo
é solução de uma equação então o seu complexo conjugado também é solução dessa mesma
equação”.
EP3.2 Resolva em C as seguintes equações de coeficientes reais:
i. z 3 − 2 z 2 + 2 z − 1 = 0
ii. z 8 − 3z 4 − 4 = 0
10
Introdução à análise complexa I
3.4. Soluções/Sugestões dos Exercícios Propostos
EP3.1 Falsa, apenas é verdadeira se os coeficientes forem todos reais.
EP3.2
i. S = 1,1 / 2 + i 3 / 2,1 / 2 + i 3 / 2
{
}
ii. Sabemos que podemos aplicar a formula resolvente a equações bi-quadráticas do tipo
z 4 + z 2 + 1 = 0 em que “olhamos” para essas equações na forma (z 2 ) + (z 2 ) + 1 = 0 , em que a
incógnita começa por ser (z 2 ) , à qual aplicamos a fórmula resolvente. Neste exercício o
raciocínio pedido é análogo. Vamos então “olhar” para a equação dada na
aplicando
a
fórmula
resolvente
forma: (z 4 )2 −3(z 4 ) − 4 = 0 ,
2
(
)
z 4 = + 3 ± 9 + 4 × 4 / 2 = (3 ± 5) / 2 ⇔ z 4 = −1 ∨ z 4 = 4. Podemos então reescrever a equação
inicial na forma: z 8 − 3z 4 − 4 = 0 ⇔ (z 4 − 4 )(z 4 + 1) = 0 . Aplicando a lei do anulamento do
produto concluímos que as soluções pedidas são as raízes quartas de 4 e de –1. Logo:
π
3π
5π
7π
i
i
i
i
⎧
⎫
S = ⎨ 2 , i 2 , − 2 , −i 2 ; e 4 , e 4 , e 4 , e 4 ⎬ .
⎩
⎭
11
Introdução à análise complexa I
4 Parametrizações de curvas
4.1- Descrição paramétrica em IR2
Definição: g:[a,b] → \ 2 , a,b ∈ IR, g(t)= ( x(t), y(t) )
⎧x ( t ) = 5 cos t
,0 ≤ t ≤ 2 π
Exemplo: A partir da descrição paramétrica ⎨
⎩ y( t ) = 5 sin t
Podemos obter a descrição cartesiana , através da “eliminação do parâmetro t”,
assim, x2(t) + y2(t) = 52cos2t + 52sen2t = 52, i.e., x2 + y2 = 25.
G
Exemplo: Uma forma prática de parametrizar um segmento de recta com origem no ponto A e
G
extremidade em B é
G
G
G
G G
g(t) = A (1-t) + B t , t ∈(0,1), ou g(t) = A + t( B - A ) , t ∈ (0,1).
4.2 Descrição paramétrica em ^
No conjunto dos números complexos existe um paralelismo muito forte entre o que
se recordou no ponto anterior e a descrição paramétrica em termos complexos.
Definição: Caminho
“Seja γ (t) = x(t) + y(t)i , a ≤ t ≤ b , em que x(t) e y(t) são funções reais, γ é um
caminho”.
Definição: Curva ou contorno3
Γ = {γ (t ) ∈ ^ : t ∈ (a, b)} é uma curva, imagem do caminho γ, i.e., Γ = γ ([a, b ]) .
Exemplo: Segmento de recta.
Uma forma prática de parametrizar um segmento de recta com origem no complexo z1 e
extremidade no complexo z 2 é γ (t ) = z1 + t (z 2 − z1 ) , t ∈(0,1).
Exemplo: O caminho γ (t) = t + ti , t∈(0 , 1) representa um segmento de recta
com extremidades γ (0) = 0 e γ (1) = 1+i .
Exemplo: Circunferência.
Uma forma prática de parametrizar uma circunferência de raio R e centro no complexo z 0 é
γ (t ) = z0 + Re it , t ∈ [0,2π [ .
3
Termo característico da análise complexa.
12
Introdução à análise complexa I
Exemplo: Os caminhos γ1(t)=5cost+i.5sint , t ∈(0, 2π) e γ2(t)=5cos(2t)+i.5sin(2t),
t ∈(0, 2π) representam uma circunferência centrada na origem de raio 5.
Exemplo: O caminho γ (t ) = 2 + 2i + 5e it , t ∈ (0, π ), representa uma semicircunferência, com y>0, centrada no complexo z0=2+2i e raio 5.
Definição: Caminho simétrico
“Seja Γ = {γ (t ) ∈ ^ : t ∈ [ a, b ]} então − Γ = {γ (a + b − t ) ∈ C : t ∈ [a, b]}”.
Definição: Contorno simples ou contorno de Jordan
“Se γ (t1 ) = γ (t 2 ) então t 1=t 2 ”.
4.3. Exercícios Propostos
EP4.1 Represente:
i.
γ 1 (t ) = 1 + e it / 2 , t ∈ [− π, π] ;
ii.
γ 2 (t ) = 1 + i + e − it / 2 , t ∈ [− π, π] ;
iii.
γ 3 (t ) = cos t + i (2 sin t − 1) , t ∈ [− π, π] .
EP4.2 Construa uma parametrização para:
i.
segmento de recta que une 1 a 2+i;
ii.
recta que passa em 1e 2+i.
EP4.3 Represente o caminho:
θ
− + iθ
⎧
, θ ∈ [0,2π[
π
⎪
e
α
γ α (θ) = ⎨
⎪⎩α (θ − 2π ) 1 − e −2 + e −2 , θ ∈ [2π,2π + 1]
[
(
)
]
em que α > 0.
13
Introdução à análise complexa I
5
Representação no plano complexo
Exercicio 5.1 : Represente no plano complexo ou plano de Argand.
i.
ii.
iii.
iv.
v.
∈ C : |z-2|<3 }
∈ C : 3≤|z|<5}
∈ C : z = 2 + i + re iθ , r<2, π < θ ≤ 2π }
∈ C : | 2z-3i+4|≥4}
{ z ∈ C : |(z-i)(1- 3 i)|=|2z|}
{z
{z
{z
{z
14