1. Nesta figura, está representada, de forma esquemática, a órbita

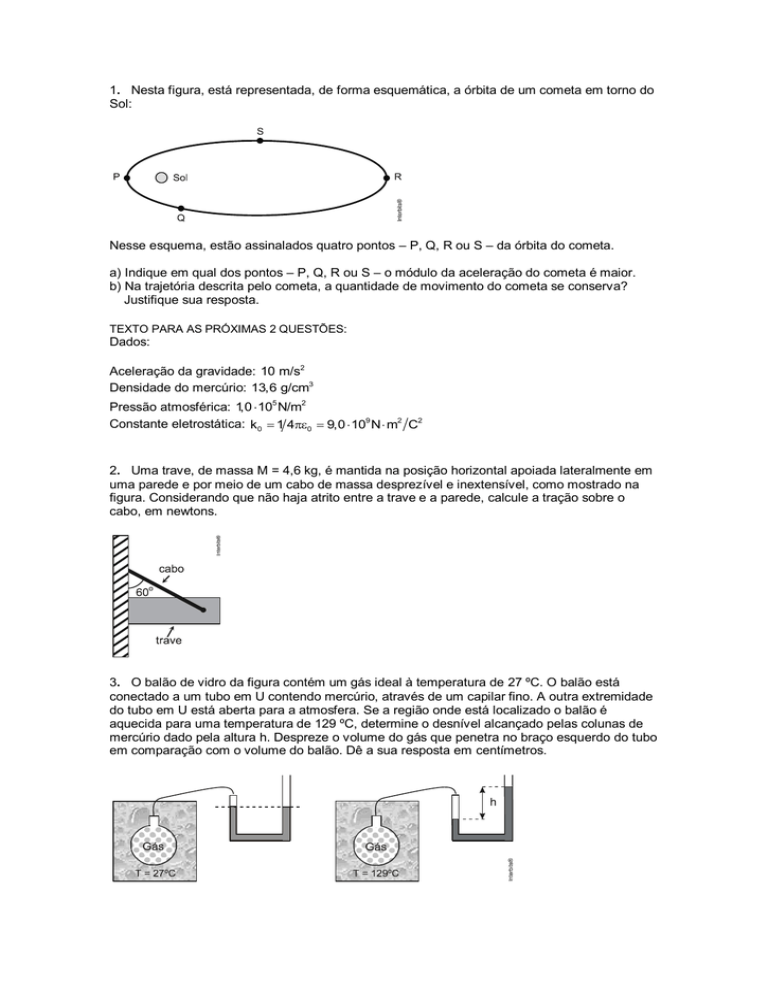
1. Nesta figura, está representada, de forma esquemática, a órbita de um cometa em torno do
Sol:
Nesse esquema, estão assinalados quatro pontos – P, Q, R ou S – da órbita do cometa.
a) Indique em qual dos pontos – P, Q, R ou S – o módulo da aceleração do cometa é maior.
b) Na trajetória descrita pelo cometa, a quantidade de movimento do cometa se conserva?
Justifique sua resposta.
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Dados:
Aceleração da gravidade: 10 m/s2
Densidade do mercúrio: 13,6 g/cm3
Pressão atmosférica: 1,0  105 N/m2
Constante eletrostática: k0  1 40  9,0  109 N  m2 C2
2. Uma trave, de massa M = 4,6 kg, é mantida na posição horizontal apoiada lateralmente em
uma parede e por meio de um cabo de massa desprezível e inextensível, como mostrado na
figura. Considerando que não haja atrito entre a trave e a parede, calcule a tração sobre o
cabo, em newtons.
3. O balão de vidro da figura contém um gás ideal à temperatura de 27 ºC. O balão está
conectado a um tubo em U contendo mercúrio, através de um capilar fino. A outra extremidade
do tubo em U está aberta para a atmosfera. Se a região onde está localizado o balão é
aquecida para uma temperatura de 129 ºC, determine o desnível alcançado pelas colunas de
mercúrio dado pela altura h. Despreze o volume do gás que penetra no braço esquerdo do tubo
em comparação com o volume do balão. Dê a sua resposta em centímetros.
TEXTO PARA A PRÓXIMA QUESTÃO:
Use quando necessário:
- Aceleração da gravidade g  10m / s2 ; Densidade da água   1,0g / cm3  1000kg / m3
- Velocidade da luz no vácuo c  3,0  108 m / s
- Constante de Planck h  6,63  1034 J  s  4,14  1015 eV  s;
- Constante   3,14
4. Um estudante de Física faz um experimento no qual ele prende duas esferas de
densidades 1 e 2 e raios r1 e r2 relacionados por 1  2 2 e r1  2r2  10,0cm . O
estudante amarra as esferas com um barbante de massa desprezível e coloca o conjunto
dentro de um grande tanque contendo água. Como mostra a figura a seguir, o conjunto de

esferas flutua totalmente submerso na água, mantendo uma tração T no barbante.
a) Faça diagramas de forças que atuam nas esferas e identifique cada uma das forças.
b) Calcule os módulos das forças de empuxo que atuam em cada esfera.
c) Calcule as densidades das esferas.

d) Calcule o módulo da tração T que atua no barbante.
Gabarito:
Resposta da questão 1:
a) O módulo da aceleração (a) do cometa, num ponto qualquer da órbita, é igual à
intensidade do campo gravitacional solar (gSol) nesse ponto. De acordo com a Lei de Newton
da Gravitação:
a  gSol 
GMSol
.
r2
Nota-se que a intensidade desse campo é inversamente proporcional ao quadrado da
distância do cometa ao Sol (r). Logo, o módulo da aceleração do cometa é maior no ponto P,
no qual essa distância é menor.
b) Entendamos aqui, Quantidade de Movimento, como Quantidade de Movimento Linear ou
Momento Linear (Q = m v), sendo m a massa do cometa e v a sua velocidade.

A figura mostra a força gravitacional F trocada entre o cometa e o Sol.
 
Essa força tem duas componentes: tangencial e centrípeta. Considerando a velocidade do

cometa no sentido indicado, a componente tangencial Ft tem o mesmo sentido da
 
velocidade. Isso nos faz concluir que o movimento do cometa de R (afélio) para P (periélio) é
acelerado, ou seja, o módulo da velocidade é crescente. Portanto, a Quantidade de
Movimento Linear (Q = m v) é crescente de R para P e decrescente de P para R.
Portanto: na trajetória descrita pelo cometa a Quantidade de Movimento não se conserva,
variando em módulo, direção e sentido.
Outra maneira de concluir é notar que o sistema é conservativo. No deslocamento de P para
R a energia potencial gravitacional aumenta, acarretando diminuição na energia cinética e,
consequentemente, na velocidade, reduzindo a Quantidade de Movimento Linear do
cometa.
OBS: num movimento curvilíneo, na ausência de torque externo (como é o caso), ocorre
conservação da Quantidade de Movimento Angular ou do Momento Angular. Porém, esse
tópico não faz parte do conteúdo lecionado no Ensino Médio. Por isso a solução foi dada
apenas em termos da Quantidade de Movimento Linear.
Resposta da questão 2:
Considerando que a força peso atue no ponto onde o fio se une com a barra, teremos:
Com a barra em equilíbrio, podemos afirmar que a resultante das forças que atuam na barra é
igual a zero, ou seja:
P  T.cos 60º  M.g  T.cos 60º
Substituindo os valores:
M.g  T.cos60º  4,6.10  T.0,5
T  92N
Resposta da questão 3:
Analisando os vasos comunicantes teremos:
Situação inicial
P1gás  Patm
Situação final
PA  Patm  Phidrostática  PA  Patm  d.g.h
P2gás  PA  P2gás  Patm  d.g.h
O gás preso no balão sofre uma transformação com volume constante (Despreze o volume do
gás que...), ou seja, podemos escrever:
P1gás P2gás

T1
T2
Substituindo as equações:
P
P
 d.g.h
P1gás P2gás

 atm  atm
T1
T2
T1
T2
Substituindo os valores:
Patm=1,0.105 N/m2
dmercúrio=13,6 g/cm3 = 13,6.103 kg/m3
P1gás P2gás
1,0.105 1,0.105  13,6.103.10.h



 h  0,25m
T1
T2
300
402
h=25cm.
Resposta da questão 4:
a)
c) Calculemos, primeiramente, as densidades das esferas para podermos resolver [B] e [D].
Dados: ρágua  1 g/cm3 = 103 kg/m3; g = 10 m/s2; π  3,14; ρ1  ρ2 / 2;
r1  2 r2  10,0 cm  r1  10,0 cm  101 m; r2  5,0 cm  5,0  102 m.
Comparando os volumes das esferas:

4
3
 V2  3 π r2

 V1  8 V2

 V  4 π  2r 3  V  8  4 π r 3 
1
2
1
2 
3

3



Se as esferas estão em equilíbrio, totalmente imersas, a densidade do conjunto (d12) é igual
à densidade da água (1 g/cm3)
m  m2
d12  1
V1  V2
d12 
ρ V ρ V
 d12  1 1 2 2
V1  V2
ρ2 V2  4  1
9V2
 1
5
ρ2
9
 d12 
 ρ2 
9
5
ρ2
 8V2   ρ2 V2
2

8V2  V2

ρ2  1,8 g/cm3  1.800 kg/m3 .
Mas:
ρ
1,8
ρ1  2 
 ρ1  0,9 g / cm3  900 kg / m3 .
2
2
b) Calculando os módulos dos empuxos:


3


34
1
 10   E1  41,87 N.
E1  ρágua V1 g  10   3,14  1 10

3


3

34
2
E  ρ
 10   E2  5,23 N.
água V2 g  10   3,14  5  10
 2
3




d) Analisando a esfera 1:

4
T  P1  E1  T  ρ1V1 g  E1  T  41,87  900  3,14  10 1
3
T  41,87  37,68  T  4,19 N.

3

10  

