D - Energia

GABARITO
Matemática D – Extensivo – V. 3
Exercícios
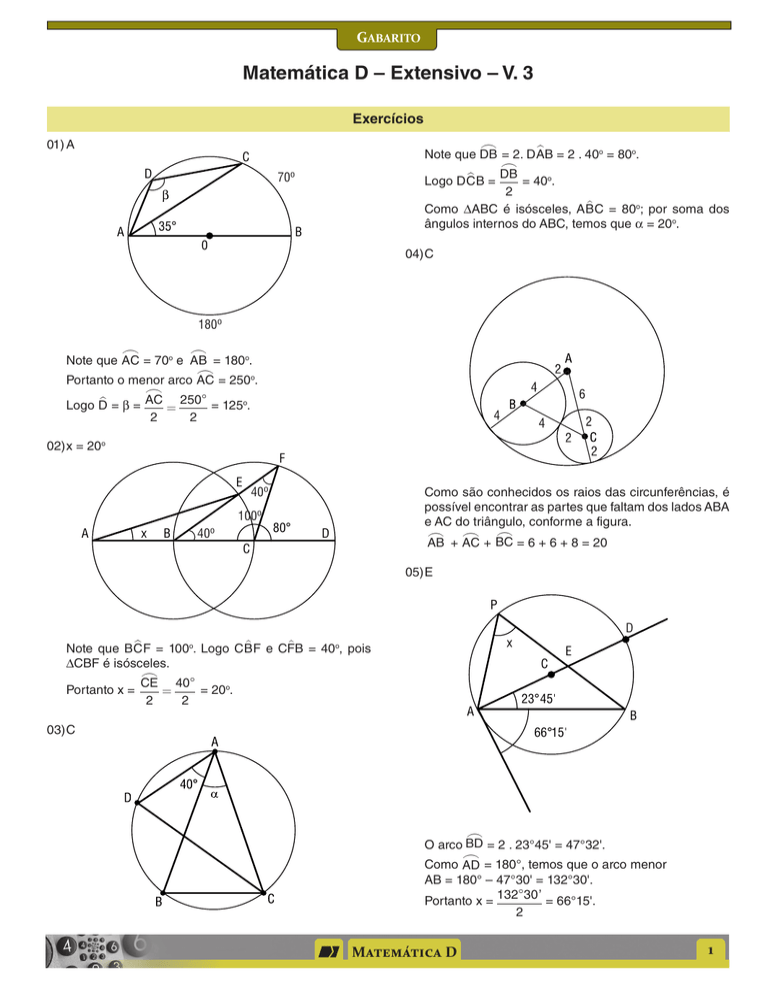
01)A
B = 2 . 40o = 80o.
= 2. DA
Note que DB
B = DB = 40o.
Logo DC
2
C = 80o; por soma dos
Como ΔABC é isósceles, AB
ângulos internos do ABC, temos que α = 20o.
C
D
70º
β
35°
A
B
0
04)C
180º
= 180o.
= 70o e AB
Note que AC
= 250o.
Portanto o menor arco AC
250°
= β = AC
Logo D
= 125o.
=
2
2
02)x = 20o
F
E
40º
100º
A
x
B
40º
80°
D
C
Como são conhecidos os raios das circunferências, é
possível encontrar as partes que faltam dos lados ABA
e AC do triângulo, conforme a figura.
= 6 + 6 + 8 = 20
+ AC
+ BC
AB
05)E
P
D
B = 40o, pois
F e CF
F = 100o. Logo CB
Note que BC
ΔCBF é isósceles.
40°
CE
Portanto x =
= 20o.
=
2
2
x
E
C
23°45'
A
03)C
B
66°15'
= 2 . 23°45' = 47°32'.
O arco BD
= 180°, temos que o arco menor
Como AD
AB = 180° – 47°30' = 132°30'.
132°30 ’
= 66°15'.
Portanto x =
2
Matemática D
1
GABARITO
06)D
P
Q
x
= 100°
AB
BCP = 194°
t
66º
valem:
e AP
Observe que os arcos menores BD
BD = BCP – PCD = 194° – 180° = 14°
A
7º
= 360° – (BCP
+ AB
) = 360° – 294° = 66°
AP
D e AB
P valem:
Portanto os ângulos BP
14
°
66
°
P =
D =
BP
= 33°
= 7° e AB
2
2
Q = 83°.
Como QPD = 90° e BPD = 7°, então BP
Por soma dos ângulos internos ΔBPQ, temos que:
P + BP
Q)
x = 180° – (AB
x = 180° – 116°
x = 64°
C
0
194º
33º
100º
= 180°
PCD
D = 90°
QP
B 14ºD
07)A
B
A
α
P
α
β
180 – β
E
α
C
D
D = β.
P = α e BA
Considere AD
Como AP = AD, então APD = α.
C são opostos ao mesmo arco, temos que:
Como α e AB
AB C = α
Por soma dos ângulos internos ΔDAP e ΔAEB, temos
respectivamente que:
2α + β = 180° 3α = 360° 2α = 60°
,
e

 α + β = 90°
α = 120°
α = 30°
08)B
B
45º
P
160º
C = 45°, temos que DC
= 90°.
Como DA
D é igual a
E como ABC = 110°, o arco (menor) A
360° – 200 = 160°. Se considerarmos O o centro da
D = 160°.
circunferência, AO
Como PA e PD tangenciam a circunferência,
P = ODP = 90°
OA
A
160º
110º
O
C
D
2
90º
Os ângulos internos do quadrilátero APDO somam 360°.
Então:
O + AO
P + DP
A = 360°
D + OD
PA
90° + 160° + 90° + DPA = 360°
A = 360° – 340°
DP
A = 20°
DP
Matemática D
GABARITO
09)A
oposto ao ângulo de 45° mede:
O arco BC
= 2 . 45 = 90°
BC
oposto ao ângulo de 65° mede:
O arco AB
AB = 2 . 65 = 130°
mede:
Portanto o arco ADC
ADC = 360° – 90° – 130° = 140°
Dessa forma m + n =
140°
= 70°.
2
10)E
B
C
108º
A
O
108º D
Tome-se O como o centro da circunferência. Como BC
e DE são tangentes à circunferência, então:
D = OB
C = 90°
OE
Como o pentágono é regular, os ângulos internos medem 108°. Sabendo-se que a soma dos ângulos internos
do pentágono BCDEO vale 540°, então:
E = 540° – 180° – 216° = 144°
= BO
BE
E
11)A
= CO
B = 150°
BC
150
.
Portanto 3x =
2
3x = 75°
x = 25°
12)A
é diâmetro, AC
B = 90°.
Como AB
Pela soma dos ângulos internos do triângulos ABC:
C = 180° – 40° – 90° = 50°
AB
= 2 . 50° = 100°.
Portanto AC
Matemática D
3
GABARITO
13)B
B
A
35º
45°
vale:
Conforme o desenho, o arco menor BD
= 2 . 45° = 90°
BD
D = 90° = 45°
Então o ângulo BC
2
A = AB
C = 35°.
Com o mesmo raciocínio, CD
Pela soma dos ângulos internos do triângulo ABO:
B = 180° – 45° – 35° = 100°
AO
Dessa forma:
x = 180° – 100° = 80o
O
x
45º
35°
D
C
14)a)x = 20 cm
b)
AN = 3 cm
a)Note que BP e BM são tangentes à circunferência;
portanto, BP = BM = 12.
Pelo mesmo raciocínio, MC = CN = 8.
Logo:
x = BM + MC = 12 + 8 = 20 cm
A
y
y
P
N
12
0
b)Como AN = AP. (tome AN = y), então:
2y + 20 + 12 + 8 = 46
AN = y = 3
8
M
B
x
C
15)37o
C = 53°.
Note que, como OC = OB , o ângulo OB
C = 74°.
Assim o ângulo BO
Com isso, o arco BC = 74°.
Portanto α =
74°
BC
= 37°.
=
2
2
16)B
D = 110°, então:
= AO
Sabendo-se que AD
D = 180° – 110° = 70°, pois AC é diâmetro.
CO
70°
= 35°.
2
D = x = 35°.
Como AO e DO são raios, CA
C = 90°. Portanto:
Como AC é diâmetro, AB
2x + y = 90°
y = 90 – (2 . 35°)
y = 20°
4
D =
Portanto CA
Matemática D
GABARITO
17)A
B
α
P
0
mede:
Como AP é diâmetro da circunferência, o arco AC
AC = 180° – 70° = 110°
.
Portanto α vale metade do arco correspondente AC
70º
35°
C
A
Basta traçar as retas OP e OC conforme o desenho.
Dessa forma:
P = 70°
= 2 . CA
PC
110°
= 55°
2
α=
= 70, temos:
Sabendo-se que o arco correspondente BC
BEC = CD B = 35° e
110º
18)D
B
E
35º
x
70°
145º 25°
A
35º
D
B = 180° – 35° = 145°
C = AD
AE
Por ângulos opostos pelo vértice, temos que:
x = 360° – 145° – 145° – 25°
x = 45°
C
19)A
= 2 . ABD = 40°.
O arco correspondente AD
Como BD é diâmetro,
= 180° – 40° = 140°. Portanto:
AB
B = 140° = 70°
AD
2
Por ângulos opostos pelo vértice, temos:
C = 85° e α = 180° – 85° – 70° = 25°
BE
20)A
A
C
α
P
0
40°
Q
D
B
E
D = β.
Considere o ângulo CB
Sabendo-se que BC E = 180° – α, temos:
(180° – α) + β + 40° = 180°
β = α – 40° (I)
Como 2β + 2α = , então:
α + β = 80° (II)
Substituindo (I) em (II), temos:
α + (α – 40°) = 80°
2α = 120°
α = 60°
Matemática D
5
GABARITO
21)D
1
x
C
= x.
Tenha-se o arco DC
D
α
A
B
0
x
2
Pelo desenho 1, concluímos que:
x
α = 90° – (I)
2
x
2
Através do desenho 2, concluímos que:
3x = 180°
x = 60° (II)
C
D
x
x
Substituindo (II) em (I), temos:
60°
α = 90° –
⇒ α = 60°
2
x
A
0
B
22)a)48 m2
b)R$ 96,00
C = 90°. Por Pitágoras e toa)Como CB é diâmetro, então BD
mando-se BD = x:
x = 102 − 82 = 6 m
• Área da região retangular (Ar):
Ar = 8 . 6 = 48 m2
b)Basta substituir a área do quadrado da área do círculo e multiplicar o resultado pelo preço do metro quadrado da grama.
• Área do círculo (Ac):
Ac = π . r2 = 3,2 . 25 = 80 m2
• Área sombreada (As):
As = Ac – Ar = 80 – 48 = 32 m2
• Valor gasto (V):
V = 32 . 3 = 96
23)26
01. Falso. Para um triângulo ser isósceles, basta
que apenas dois de seus lados sejam iguais,
enquanto que, para ser equilátero, todos os
seus lados devem ser iguais.
02.Verdadeiro. O suplemento de um ângulo α é:
x = 180° – α. Portanto nesse caso:
x = 180° – 120° = 60°
04.Falso. A soma dos lados que medem 17 e 13
é igual a 30, que corresponde ao terceiro lado.
6
08.Verdadeiro. O número de vértices de um polígono é dado
n(n − 3) 10 . 7
= 35.
por: P =
=
2
2
16.Verdadeiro.
360°
• = 20
18°
• Pc = 2 . π . r = 20π
20π
• = π
20
Matemática D
GABARITO
24)B
P
2R
q
R
R
Basta verificar que as únicas maneiras de uma circunferência tangenciar as duas circunferência concêntricas
ao mesmo tempo são:
01. Uma circunferência de raio R com centro em P.
02.Uma circunferência de raio 2R com centro em q.
25)D
t
B
A
4
2
P
Q
Observe que os triângulos PAR e PBQ são semelhantes.
Portanto podemos chegar à seguinte relação:
2 2+x
=
4 8+x
8 + 4x = 16 + 2x
2x = 8 ⇒ x = 4
Portanto:
PQ = 4 + 4 + 4 = 12
s
26)D
Pela figura vemos que o raio da circunferência inscrita
é a. Por Pitágoras, temos:
2
2
R = a +a
2
R = 2a
R=a 2
Portanto a razão será:
a
1
2
2
=
.
=
2
a 2
2
2
27)E
B
Traçando-se a reta CP , tem-se o triângulo APC.
C = 90°.
Como AB é tangente, o ângulo AP
Como AP = 3 3 , é possível usar a função trigonométrica
P
r
C
0
tg(30°) =
60º
30º
A
r
. Assim:
3 3
3
r
=
⇒r=3
3
3 3
Matemática D
7
GABARITO
28)A
Basta colocar o raio (r) em função do lado (l) do quadrado.
Por Pitágoras:
2r =
r
2 + 2
2
2
Perímetro do quadrado (P): P = 4l
Comprimento da circunferência (C):
2
= πl 2
C = 2π .
4
Razão: π 2 = π 2
4
4
2r = l 2 ⇒ r =
r
29)B
A área da figura corresponde à soma das áreas das
circunferências maior e intermediária dividida por dois.
π . 62 π . 32 36π 9π
Af =
= 22,5 π cm2
+
=
+
2
2
2
2
O perímetro é igual à soma da metade dos perímetros
das quatro circunferências.
Pf = 2π .1, 5 + 2π .1, 5 + 2π . 3 + 2π . 6
2
2
2
2
Pf = 3π + 3π + 6π = 12π
30)A
π
corresponde a um arco de
5
8π m, então meia circunferência tem comprimento:
Cm = 5 . 8π m
Cm = 40π m
Como meia circunferência é
2πr
Cm =
= πr, então:
2
πr = 40 πm
r = 40 m
Sabendo-se que o ângulo
31)B
Conforme a figura, é possível perceber que
4x + 6° + x + 24° + 2x – 20° = 360
7x = 360° – 10o
x = 50°
mede:
Portanto a medida do ângulo A
= x + 24 = 74° = 37°
A
2
2
8
Matemática D
GABARITO
32)A
R
9
Primeiro encontramos o valor de r, sabendo que o
comprimento da circunferência menor é 32π:
2πr = 32π ⇒ r =16
Dessa forma podemos achar R:
R – r = 9 ⇒ R = 25
r
Agora, por Pitágoras, é possível encontrar CD :
(R + r)2 = 92 + (CD )2
CD = 40
r
r
33)D
Conforme a figura, basta utilizar Pitágoras para descobrir x:
52 = 32 + x2
x = 25 − 9 = 4
Portanto a corda tem comprimento igual a 8.
34)C
Pela reação métrica entre duas cordas, temos que BE . ED = AE . EC .
AE . EC = 6 . 8 = 48
48
(I)
EC
Como AE = 1 , então AE = EC (II).
EC 3
3
Igualando (I) e (II) temos:
EC = 48 ⇒ EC = 144 = 12
3 EC
12
= 4, AC = 12 + 4 = 16
AE =
3
AE =
35)E
A
x
B
2,5
2,5
O
6 cm
P
AP . AB = (AT)2 ⇒ (5 + x)x = 36
x2 + 5x – 36 = 0 ⇒ x' = –9 ou x" = 4
Logo x = 4
T
Matemática D
9
GABARITO
36)B
39)E
(PA)2 = PB . PC
(3PC)2 = PB . PC
9PC2 = PB . PC
PB = 9PC
37)E
A
6
D
10
7
B
Pela relação métrica entre secante e tangente, temos.
82 = x . (2x)
2x2 = 64
x = 32
x=4 2
x
4
E
C
40)E
AE . AD = AC . AB
10 . 6 = (x + 7) . 7
60 = 7x + 49
7x = 11
x = 11
7
r
E
r
0
4cm
D
A
8cm
38)E
B
10cm
D
C
2α
C
α
B
2α
α
A
0
Por potência de um ponto exterior, concluímos que:
AB . AC = AD . AE
8 . 18 = 4 . (4 + 2r)
8r + 16 = 144
r = 16
Portanto P = 16 + 16 + 4 + 18 = 54.
41)04
A
2
D = α.
Primeiramente adotemos o ângulo AB
Posteriormente, trocando OC = OD , concluímos que
O = 2α.
O = CD
DC
2
r
Por último tem-se que
D = 180 – 4α e AO
C = 180 – α.
CO
Como AOD = AOC – COD, temos:
D = 180 – α – (180 – 4α)
AO
D = 3α
AO
r
8
10
r
Matemática D
r
r
B
6
C
GABARITO
Pela figura note que os lados do trapézio valem 10 cm.
Portanto, para descobrir o raio, basta resolver Pitágoras
no triângulo ABC:
102 = (2r)2 + 62
4r2 = 100 – 36
64
r=
4
r=4
42)C
b)
Pela relação de potência de um ponto exterior, temos:
7 . 16 = 8(8 + x)
8x = 112 – 64
x=6
Obs: Note que o gabarito está errado.
c) A
P e
Basta traçar a reta BE e encontrar os ângulos EB
BEP:
P = 90° + 36° = 63°
EB
2
P = 124° + 36° = 80°
BE
2
Portanto:
x = 180 – 80 – 63 = 37°
43)a)x = 12
b)x = 6
c)x = 5
x
B
4
P
6
Por potência de um ponto externo, temos:
62 = 4(4 + x)
4x = 36 – 16
x=5
44)C
a)
Por potência de um ponto interior, temos:
2x = 4 . 6
x=2.6
x = 12
Note pela figura que, tomando-se
AP = x e DQ = y;
EF = x – 3 + y – 6 e BC = x – 4 + y – 5.
Conclui-se que:
BC – EF = x – 4 + y – 5 – (x – 3 + y – 6)
BC – EF = 0
Matemática D
11
GABARITO
45)D
x + b
Traçando-se a reta DO forma-se o triângulo retângulo
ADO.
O = 30°:
Por cosseno do ângulo DA
cos 30° =
0
x=
x
a
a
x
4
4 3
⇒ x = 2 3
2
48)A
b
Por potência de um ponto interior:
a . a = b (2x + b)
a2 – b2 = 2bx
2
x = a −b
2b 2
2,5
2,5
P
d
Q
0
2,5
46)A
6
S
Pela relação de potência de um ponto exterior, temos:
62 = (d + 5) . d
d2 + 5d – 36 = 0
S = –5 e P = –36 ou d = 4 ou d = –9
Como d é distância, então excluímos d = –9.
49)C
Basta somar as metades dos comprimentos das quatro
circunferências.
2π + 4π + 6π + 8π 20π
=10π = 30 m
D=
=
2
2
Sabendo-se o comprimento total da espiral (D), basta
dividi-lo pelo tamanho do tijolo.
30
N=
= 100 tijolos
0, 3
47)E
B
A
x/2
30º
2
O comprimento da semi circunferência (C) é dado por:
2πr
= π . 6370
C=
2
Tome π = 3,14; então C = 20001,8 km
Como o avião faz 800 km em uma hora, basta dividir
"C" pela velocidade:
20001, 8
T=
≅ 25
800
50)D
D
60º
C
0
Do enunciado verifica-se que o triângulo BCO é equi B = 180° = 60°. Portanto o arco
látero; logo CO
3
BC = 60° e o ângulo BAC = 30°.
12
Matemática D
GABARITO
a)Errada. ABCDEF é a soma do comprimento do círculo
formado pela soma dos dois semicírculos com a reta DC
.
ABCDEF = 2 . π . R + 100 = 310 m
b)Errada. ABCD é a soma do semicírculo ABC + CD .
2πR
+ 100 = 205 m
ABCD =
2
2πR
c)Errada. ABC =
= 35 . 3 = 105
2
d)Certa. A volta completa (D) é a soma:
+ DEF
+ DC + AF ,
ABC
D=
Por potência de um ponto interior, temos:
7(7 + x) = 6 . 10
49 + 7x = 60
60 − 49 11
x=
=
7
7
53)D
A
B
128°
D
2(2πR)
+ 200 = 410 m
2
x
51)A
C
Pelo desenho é possível ver que
BAD
= 128o . 2 = 256o
x=
e BCD
2
= 360o – BCD
= 104°.
⇒ BAD
Como BAD
Então:
104
x=
= 52°
2
Por potência de um ponto interior, temos:
10x = 6
x = 0,6
52)A
54)C
Idem ao exercício 34.
55)B
Por potência de um ponto exterior, temos:
(2PA)2 = PA(PA + 18)
3PA2 – 18PA = 0
36
=6
PA =
6
Matemática D
13
GABARITO
56)20
x+1
Basta traçar as retas MD, AD e AC.
Como CD é diâmetro, então o triângulo ACD é retân D com o triângulo retângugulo e partilha o ângulo AC
lo ACM. Portanto, por semelhança de triângulos, o
M.
M = AD
ângulo CA
Como os triângulos AMC e AMD são retângulos e
M e o lado AM , por semelhança
partilham o ângulo AD
2x
3x
de triângulos, temos:
M = AC
M
DA
3x + 1
Portanto por semelhança de triângulos:
40 80
=
x
40
2x = 40
x = 20
Sabendo-se que a média aritimética entre os lados
opostos de um trapézio são iguais, então:
x + 1+ 3x + 1 3x + 2x
=
2
2
4x + 2 = 5x
x=2
Portanto: 3 . 2 + 2 + 1 + 2 . 2 + 3 . 2 + 1 = 20.
57)6
A
4
Logo, o raio (r):
100
r=
= 50
2
O comprimento (C):
C = 2 . π . R = 100π
B
4
r
59)E
F
9
r
Idem ao exercício 27.
60)C = 2r . (4 + π)
A
D
E
9
4
5
Por Pitágoras, no triângulo retângulo BEF, temos:
(2r)2 = 132 –25
2r = 169 − 25
12
r=
=6
2
D
M
A
40
B
40
80
G
r
r
r
r
C
F
r
r
E
Pela figura note que o comprimento da correia é


8 . r + 4 .  2πr , ou seja, oito vezes o raio mais quatro
 4 
vezes um quarto do comprimento da circunferência.
4 . 2πr
= 8r + 2πr = 2r . (4 + π)
C = 8r +
4
C
14
H
B
D
58)B
r
C
Pela figura note que
CF = CD = 9 e AB = BF = 4
r
Matemática D
GABARITO
61)A
Q
Pelo desenho temos:
x2
+ 4(x – 3) + 3(x – 4) + 12
x2 =
2
x2
= 4x – 12 + 3x – 12 + 12
2
x2 = – 14x + 24 = 0
x' = 12 e x" = 2
M
16
N
O
16
A
P
Note que não podemos ter x = 2, pois os lados do jardim
ficariam com medidas negativas.
122 144
= 72
Então A =
=
2
2
Pela figura notemos que AP = AN e QM = QN.
Portanto o perímetro do triângulo é:
P = 2 . 16 = 32
64)A
F
62)E
1
E
Basta usar
Pitágoras
para achar
A
√3.
D
E
B
√3
C
A
1
2
D
Basta contar as diagonais.
Mas note que AD = BE = FC = 2 e.
FD = FB = EA = EC = DB = CA =
Seja d a diagonal de cada quadrado.
Então, por Pitágoras, temos:
d2 = (4 2 )2 + (4 2 )2 = 16 . 2 + 16 . 2
d2 = 64 ⇒ d = 8
Logo:
A = 2d . 3d = 6 . 64 = 384
63)A
3
Logo (AD + BE + FC) = 2 + 2 + 2 = 6 e
FD + FB + EA + EC + DB + CA =
3 + 3 + 3 + 3 + 3 + 3 =6 3
Portanto a soma dos comprimentos das diagonais é
igual a 6 + 6 3 .
65)C
Os ângulos internos de um pentágono medem 108°.
Como o pentágono é regular, as retas AC e CE estão
em três. Portanto:
dividindo C
α=
108
= 36°
3
Matemática D
15
GABARITO
66)B
Como o hexágono é regular, os ângulos internos medem
C = 120° = 60°.
120°. Portanto o ângulo AB
2
Tome BC = x. Então x pode ser encontrado por tg(30°).
6
r
30º
3
Pela figura temos que r pode ser encontrado usando a
função cosseno em 30°.
3
3 3
= ⇒r=2 3
cos 30° = ⇒
r
r
2
x
5 3
3 x
= ⇒
⇒
5
5
3
3
Portanto o perímetro (P) é:
5 3
P = 12 .
= 4 . 5 3 = 20 3
3
tg(30°) =
69)V – F – V – V – V
r 45º
r
67)A
r
30º
a
a
2
R
r
a)Verdadeiro. x pode ser calculado usando
cos 45° = x ⇒ x = 2 r . Portanto o lado do quadra2
r
a
2
a
Pelo desenho note que r e R podem ser encontrados
pela tg (30°) e cos (30°) respectivamente.
a
r
• tg (30°) = • cos (30°) = 2
a
R
2
3
a
3 = 2r R.
=
2
2
3
a
3a 3a
R=
3
6
R
Portanto a razão é:
r
R 6 3a
=2
=
r
3 3a
r =
68)A
x C
60º
60º
30º 5cm
B
60º
A
do vale: 2x = 2 . 2 r = 2r
2
b)Falso. Pelo desenho note que o lado do quadrado
circunscrito vale 2r. Portanto a razão (R) vale:
2r
2 2
R=
=
= 2.
2
2r
c)Verdadeiro. Pelo desenho temos que o apótema do
quadrado circunscrito é r e o do inscrito é x. Portanto
a diferença (d) vale:
d = 1 – 2 = 2− 2
2
2
d)Verdadeiro. Perímetro dos quadrados:
Pc = 4 . 2r = 8r
Pi = 4 . 2r
Razão dos perímetros (Rp):
8r
2 2
Rp =
=
4. 2 r
2
Razão dos apótemas (Ra):
r
2r
2 2
=
Ra =
=
2
2r
2r
2
e)Verdadeiro. Área dos quadrados:
Ac = 2r . 2r = 4r2
Ai = 2r . 2r = 2r2
Razão entre as áreas (Ra):
4r 2
Ra = 2 = 2
2r
16
r
Matemática D
GABARITO
70)D
Basta formar os triângulos DEQ, AEP e BCR. Como o
hexágono é equiângulo, os triângulos são equiláteros
e, por consequência, o triângulo PRQ também é equilátero. Portanto:
x + 23 + 15 = 20 + 13 + 15
x = 10
10 + 20 + y = 48
y = 18
Logo:
P = 18 + 10 + 23 + 15 + 13 + 20 = 99
60º
45º
73)12
Pela figura concluímos que o lado do quadrado é dado
por:
2R
cos 45° = x ⇒ x =
, l = 2 . x = 2R
2
r
B
e a do hexágono por:
R
y
cos 60° = ⇒ y = , L = 2y = R
2
R
3√ 3
0
r
30º
A
A diferença é dada por:
d = 2 −1 R
2
71)D
C
Pela figura note que, como ABC é equilátero, o ângulo
O vale 30°. Portanto por cosseno de 30° é possível
BC
encontrar r:
6 3
cos 30° = 3 3 ⇒ r =
=6
3
r
Portanto o lado (l) vale:
l = 2 . 6 = 12
74)E
F
A
Sendo os pentágonos regulares, então α = 108°. Portanto:
θ = 360° – 3 . α = 360° – 324° = 36°
72)99
E
B
Q
P
a
2
C
D
20
E
20
20
H
D
13
y
C
F
15
P
x
A
23
G
0
1
B
15
15
Pela figura note que o triângulo EOP é isósceles e PE
O = POE = 45°.
Portanto:
a
a 2
a
cos 45° =
⇒ EO =
=
2
2
2
EO
R
Matemática D
17
GABARITO
77)D
 a 2 
Logo a = 2 
− 1 .
 2

L
a=a 2–2
a=
2
2 −1
r
75)E
45º
B
3
3
o
r
30º
A
3
2
D
C
Pela figura vemos que ADO é um triângulo retângulo,
O = 30°. Portanto:
com ângulo DA
cos 30° =
3
3
3 3
⇒r=
=
=
2
3
3
r
Pela figura note que o lado do quadrado circunscrito
pode ser encontrado por:
2
⇒
=
⇒l= 2 .r
cos 45° =
2
2
2
r
r
Portanto a razão (R):
2r
2
R= =
=
L
2r
2
78)D
3
76)D
x
45º
r
Pela figura vemos que o apótema é igual à metade do
lado do quadrado.
Portanto:
2 x
= ⇒x=3 2
cos 45° = x ⇒ x =
6
2
r
Como o hexágono é regular, temos que:
w° = 120°
v = 90°
y° = 60°
x = 30°
z° = 90°
79)A
x
r
Logo o lado do quadrado vale 6 2 e o apótema vale
x
3 2.
r
Sejam r e x o raio da circunferência e o lado do quadrado respectivamente, então:
(2r)2 = x2 + x2 ⇒ 2x2 = 4r2 ⇒ 2 . r
18
Matemática D
GABARITO
Portanto, o perímetro = 4 . x = 4 . 2 . r
Logo
2π r
comprimento
π 2
.
=
=
perímetro
4
4 2r
80)2 5
E
2√
2
B
2
A
2√
2
2
Seja x = FE = FD.
Então:
AD = AC = 1 + x
Note que são semelhantes os triângulos ΔACF e ΔDEF.
Então temos que:
FA FD
1
x
=
⇒
=
x
+
1
1
AC DE
⇒ x(x + 1) = 1 ⇒ x2 + x – 1 = 0
−1± 1+ 4 −1+ 5
=
x=
2
2
Perceba que x tem de ser maior que zero, pois trata-se
de uma distância, que é sempre positiva.
−1+ 5
.
Logo x =
2
Portanto:
−1+ 5 −1+ 5
=
, e essa é a raíz
AD = 1 + x = 1 +
2
2
positiva da equação x2 – x – 1 = 0.
45º
D
2
82)C
C
Note que AB = 2.
(área = 4)
Seja CE = x.
Pela lei dos cossenos aplicada ao triângulo ΔCED,
temos que:
2
2
x2 = CD + DE – 2CD . DE . cos 45°
2
x2 = 22 + (4 2 )2 – 2 . 2 . 4 2 .
2
x2 = 4 + 16 . 2 – 8 . 2
x2 = 4 + 16(2 – 1)
x2 = 20
x = 20
x =2 5
p = a + b + c ⇒ p = 8 + 7 + 9
2
2
p = 24 = 12
2
Semiperímetro
↑
↑
Então: S = p(p − a)(p − b)(p − c)
S = 12(4 . 5 . 3) = (4 . 4 . 9 . 5)
81)E
A
5 = 12 5
83)D
1
E
S=2.2.3.
1
x
B
F
1
x
D
1
C


2R = 52 + 52 = 50
Matemática D
19
GABARITO
R=
50
2
2


= a2 1+ 3 

2 
2
a
3
A = a2 +
4
AC


A = 4 . 5 . 5 = 50 cm2 ⇒ A○ = πr2 = π 50 
 2 
2
A○ = π . 50 25 π cm2
=
4
2
A área hachurada (A ) é a diferença entre a área do
quadrado (A ) e a área da circunferência (A○) dividida
por 4:
25π 100 − 25π
50 −
= 25 . (4 – π)
A = A − A○ =
2
2 =
4
4
4
8
84)C
r ⇒ A = πr2
1
A
A
D
=A
2
A
=



3 
3 
3 
3
2
2
− 1−
a 2 1+
 − a 1+
 a 1+


2
4
2
4
=
=
=
2
2
3
2
a2 .
4 =a 3
=
8
2
87)A
I.
2r
2
⇒ A2 = π(2r)2 = 4
πr
↓
↓
4 . A1
p = a +b +c
2
10 + 10 + 12
p=
= 16
2
S = p(p − a)(p − b)(p − c)
85)D
1
S1 = 16 . 6 . 6 . 4 = 4 . 6 . 2 = 48
F = 90°.
Note que EB
Assim:
EB . BF
2 3. 2 3
S=
⇒ S =
=2.3=6
2
2
86) E
A
√3
2
a
B
a
a
20
10 + 10 + 16
p = a + b + c ⇒ p =
= 18
2
2
S = p(p − a)(p − b)(p − c)
2
S2 = 18 . 8 . 8 . 2 = 3 . 4 . 4 = 48
S1 = S2
E
a
a
C
II.
a
D
Matemática D
GABARITO
90)B
88)B
C
C
E
6
A
B
~
A
D
D
A
B
E
5
A
5
x=
2
D
α
B
C
3 x
=
6 5
B = 60°,
Do fato de que AO
ΔABC é equilátero, pois DC é perpendicular a AB .
Logo A A B = AB . DC .
2
C
Vamos deixar r = AB em função de α.
x = 15 = 5
6
2
5
. 3 15
S = AD . 3 = 2
=
2
2
4
2
2

r   3
2

Note que   + 
⇒
 2   2 r + r  = α
89)E
r 2 3r 2 + 4 3 r 2 + 4r 2
8r 2 + 4 3 r 2
+
= α2 ⇒
= α2
4
4
4
(8 + 4 3 )r 2
4
r=
= α2 ⇒
2α
8+4 3
=
2α
2 2+ 3

3 
r .r +
r
α

2  =
. Logo A =
2
2+ 3
α2
. (2 + 3 )
2
r 2 (2 + 3 ) (2 + 3 )
=
= α
=
4
4
4
Note que se AB = a,
a2 3
. Então:
P=9 3 =
4
9 . 4 3 = a2 3
a=3.2.=6
91)E
Ademais:
BC = cos 60° . a = 1 . 6 = 3
2
CD = sen 60° . a = 3 . 6 = 3 3
2
Portanto:
Q = 3. 3 .3 = 9 3
2
2
E assim:
9 3
1
1
Q
2
2
=
= =
1
P
2
9 3

ΔABC é equilátero.
122 3 144 3
=
4
4
A = 36 3
A=
Matemática D
21
GABARITO
92)B
95)D
3A1 = A2 ⇒ 3 . 72 .h = 120(h + 32) ⇒
2
2
72h = 40h + 1280 ⇒ h = 40
Note que AB = 10
(imagine a folha dobrada).
Logo, do triângulo pitagórico Δabc, temos que BC = 8.
Faça EA = h. Então DE = 8 – h.
Logo h2 = (8 – h)2 + 42 (Pitágoras no ΔDEA)
h2 = 64 – 16h + h2 + 16 ⇒ h = 5
5 .10
B
Portanto A E
=
= 25 cm2
2
A
96)C
D
60º
30º
120°
x
60º
x 30º
93)B
60°
C
x
30°
60º
B
2
4 3
2
⇒ CE =
3
CE
2 3
BE
tg 30° =
⇒ BE =
3
2
II
DE
Então (x + 2)2 = x2 + (2 3 )2.
cos 30° =
12
12
x
⇒x=9
=
20 15
20
D
E
x=9
8
A
15
x 2 + 4x + 4 = x 2 + 4 . 3 ⇒ x = 2
22 3 4 3
A =
= 3
=
4
4
B
Note que:
A
= A
– A
C
A
B
C
D
E
97)A
Portanto:
15 . 20 12 . 9 300 − 108 192
−
=
=
A =
= 96
2
2
2
2
94)A
P = 2(h + 2h) = 60
3h = 30
h = 10
Então A = 10 . 20 = 200.
22
5
Note que são 4 triângulos congruentes. Então S' = .
4
S
S
5
4
= 4.
Logo
= =
.
1 5
S’ 5
4
Matemática D
C
GABARITO
98)D
5
5
⇒x=
8
4
8−5
11
( − x)
3
A=
= 8 =
2
2
16
2x =
101)A
AA
E
D
A
A
B
C
6.4
3
= 2 =
10
10 . 8
2
99)B
O triângulo é pitagórico. Logo AC = 8.
6.8
= 24
A=
2
102)C
C
F
A
G
D
E
B
Note que AG = GD = DE = EB. Assim o ΔAFB é dividido em quatro triângulos com áreas iguais (mesma base
e mesma altura). Logo a área procurada é:
4
3
A
A
F
B
4
3
=
AA
C
B
2
=
3 96
= 36
.
4 2
(4 – x)2 – x2 = 56
x2 – 8x + 16 – x2 = 56
40
x=
⇒x=5
8
5 .9
A=
= 22,5
2
103)D
100)A
C
D
C
1
2
x
1E
x
F
G
5
x
B
A
10
3
4
G
D
8
3
Seja EF = FC = FB = x.
Então, do
x2 =
C
F
G
2
, temos: x2 =  1 + (1 – x)2.
 
2
1
2
+ 1 – 2x + x
4
E
A
De
Matemática D
CDG ∼
F
4
B
CAF:
23
GABARITO
106)70
CD 4
10
= ⇒ CD =
5
6
3
B
CDE ∼
ABC:
10
8
5
= 3 ⇒ DE =
4 DE
3
Logo:
10 8
.
A C = 3 3 = 40
2
9
D E
De
4
2
E
4
10
3
3
F
3
0
6
3
104)B
A
C
6
D
6
C
12
A
16
20
O triângulo é pitagórico. Logo CB = 16.
12 . 16
Assim A =
= 96 cm2.
2
105)D
B
Como BD = 8 e OD = 3, temos que OB = 5 e, assim, os
triângulos EOB e FOB são os pitagóricos (3 – 4 – 5).
BCD.
Por outro lado, BOF ∼
4
8
⇒ BC = 10. Logo FC = 6.
Assim =
5 BC
01. Falso. A altura é 8.
02.Verdadeiro.
04.Verdadeiro.
08.Falso. A base mede 12.
16.Falso. O centro dista mais que 6.
32.Falso. O centro dista 6,25.
12 . 8
64.Verdadeiro. A =
= 48 cm2.
2
107)D
6
3
2
3
7
1
7
3y
5x
A2 =
2
2
Note que
y 3
3x
e x + y = 4.
= ⇒y=
x 5
5
Então:
5
3x
x+
= 4 ⇒ 8x = 20 ⇒ x = = 2,5
2
5

y = 1,5
Logo:
5 . 2, 5 3 . 1, 5
=4
A2 – A1 =
−
2
2
A1 =
R=
3
2
9 3
+ + 7 + 18 = 6 + 25 = 31
2 2
108)B
C
4
4
x
2
2
2
A
24
3 9
2
18
Matemática D
2
x
B
GABARITO
(4 + x)2 = (2 + x)2 + 62
+ 36
4
2√
2
R = 2√ 2
4
2
16 + 8x + x = 4 + 4x + x
4x = 24
x=6
Logo:
6 .(2 + 6)
48
A=
⇒A=
⇒
2
2
A = 24
110)D
2
2√
2
109)C
D
10
3
10
F 3
10
E 3
C
h
A
A=
10
A=
b
=
A –A
4
+
A =
2
π r 2 − 42 42
π . 8 − 16
+ 8 = 2π + 8
+
=
4
2
4
B
b .h 10
1
= 10 cm2
. 6 .
=
2
3
2
Matemática D
25