universidade federal do rio grande do norte

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE
D EPARTAMENTO DE F ÍSICA T EÓRICA E E XPERIMENTAL
E DUARDO M OREIRA DAMASCENO
D EPOSIÇÃO DE AlN POR S PUTTERING NÃO R EATIVO .
D ISSERTAÇÃO DE M ESTRADO
NATAL ,RN
D EZEMBRO DE 2010
E DUARDO M OREIRA DAMASCENO
D EPOSIÇÃO DE AlN POR S PUTTERING NÃO R EATIVO .
Trabalho apresentado ao Programa de Pósgraduação em Física do Departamento de
Física Teórica e Experimental da UNIVERSIDADE FEDERAL DO RIO GRANDE DO
NORTE como requisito parcial para obtenção
do grau de Mestre em Física.
Orientador:
Prof. Dr. Carlos Chesman de Araujo Feitosa
NATAL ,RN
D EZEMBRO DE 2010
E DUARDO M OREIRA DAMASCENO
D EPOSIÇÃO DE AlN POR S PUTTERING NÃO R EATIVO .
Trabalho apresentado ao Programa de Pósgraduação em Física do Departamento de
Física Teórica e Experimental da UNIVERSIDADE FEDERAL DO RIO GRANDE DO
NORTE como requisito parcial para obtenção
do grau de Mestre em Física.
Data de aprovação: __ /__ /____
BANCA E XAMINADORA
Prof. Dr. Carlos Chesman de Araujo Feitosa
DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL - UFRN
Prof. Dr. Marcio Assolin Corrêa
DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL - UFRN
Prof. Dr. Sergio André F. Azevedo
DEPARTAMENTO DE FÍSICA - UFPB
“ À querida e amada Luiza por ser minha única certeza
nesse Universo tão estranho.”
ii
Agradecimentos
Agradeço primeiramente ao Prof. Dr. Carlos Chesman de Araujo Feitosa pela orientação
durante a realização desse trabalho. Por toda motivação, dedicação, compreensão e principalmente por me abrir as portas do laboratório ensinando-me a ser um pesquisador experimental.
Aos meus pais Carlos e Eloisa pelo apoio e confiança desde quando comecei o curso de
física e por todo carinho e amor que me deram, sempre. Aos meus irmãos Danilo, Daniel e
Daniela por toda união e diversão quando estamos juntos. A minha filha Luiza, a estrelinha que
me guia. A Rebeca por todo carinho e compreensão. Aos meus famíliares e em especial aos
meus primos Paulo e Renato por todo incentivo e por acreditarem em mim.
Ao grande amigo e incentivador o Prof. Dr. Sergio Andre F. Azevedo um referencial em
minha vida acadêmica desde os tempos de graduação, sempre lhe serei grato por toda confiança
depositada. Ao Prof. Dr. Marcio Assolin por todas dicas e ensinamentos fundamentais durante
a realização desse trabalho. Ao Prof. Ilde Guedes, aos colegas José Américo e Manilo, por toda
ajuda, tornando possível a realização desse trabalho. Aos Prfs. Drs. Fernando Moraes e Claudio
Furtado (UFPB) pelo incentivo em momentos difíceis. A todos os professores e funcionários
do departamento de física da UFRN.
A todos os colegas e amigos da pós-graduação por todo companheirismo, não só nos momentos divertidos mas, principalmente nos momentos árduos durante toda essa longa trajetória.
Agradecimentos especiais aos amigos Macedo, Gabriel, Thompson, Danilo, Bruno e Caio, pela
ótima convivência. Aos amigos distantes geograficamente, mas sempre presentes, Alan, Edson,
Lula, Matheus e Vamberto. A todos que de alguma forma tornaram essa realização possível.
À UFRN, ao CNPq e a CAPES.
“ If, in some cataclysm, all scientific knowledge were to be destroyed, and
only one sentence passed on to the next generation of creatures, what
statement would contain the most information in the fewest words? I
believe it is the atomic hypothesis (or atomic fact, or whatever you wish to
call it) that all things are made of atoms - little particles that move around
in perpetual motion, attracting each other when they are a little distance
apart, but repelling upon being squeezed into one another. In that one
sentence you will see an enormous amount of information about the world,
if just a little imagination and thinking are applied. ”
—RICHARD P. FEYNMAN (1918-1988)
Figura 1 The scientist
iv
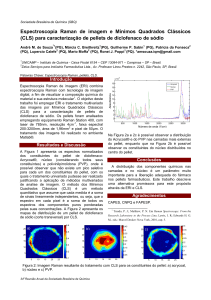
Resumo
Neste trabalho depositamos via magnetron sputtering de rádio-frequência não reativo nanofilmes de nitreto de alumínio (AlN). Os nanofilmes de nitreto de alumínio são materiais semicondutores com alta condutividade térmica, elevado ponto de fusão, piezoeletricidade e largo
"bandgap"(6, 2 eV) com estrutura cristalina wurtzítica hexagonal, pertencentes ao grupo de novos materiais denominados nitretos III-V que em conjunto com o nitreto de gálio e o nitreto
de índio têm despertado muito interesse por possuírem propriedades físico-químicas relevantes para novas aplicações tecnológicas, principalmente em microeletrônica e dispositivos optoeletrônicos. Foram depositados três grupos de nanofilmes com as espessuras dependêntes do
tempo, sobre dois tipos de substratos (vidro e silício) a uma temperatura de 25°C. Os nanofilmes
de AlN foram caracterizados usando três técnicas, a difração de raios-X, espectroscopia Raman
e microscopia de força atômica (AFM), analisado-se a morfologia desses. Através da análise
dos raios-X obtemos a espessura de cada amostra com sua respectiva taxa de deposição. A análise dos raios-X também revelou que os nanofilmes não são cristalinos, evidenciando o caráter
amorfo das amostras. Os resultados obtidos através da técnica, microscopia de força atômica
(AFM) concordam com os obtidos usando a técnica de raios-X. A caracterização por espectroscopia Raman evidenciou a existência de modos ativos característicos do AlN nas amostras
analisadas.
Palavras-chave: Sputtering, nanofilmes, nitreto de alumínio.
v
Abstract
In this work we deposit via non-reactive magnetron sputtering of radio-frequency nanofilmes of nitreto of aluminum(AlN). The nanofilms aluminum nitride are semiconductors materials with high thermal conductivity, high melting point, piezoelectricity and wide band gap (6,
2 eV) with hexagonal wurtzite crystal structure, belonging to the group of new materials called
III-V nitrides in which together with the gallium nitride and indium nitride have attracted much
interest because they have physical and chemical properties relevant to new technological applications, mainly in microelectronic and optoelectronic devices. Three groups were deposited
with thicknesses nanofilms time dependent on two substrates (glass and silicon) at a temperature of 25 ° C. The nanofilms AlN were characterized using three techniques, X-ray diffraction,
Raman spectroscopy and atomic force microscopy (AFM), examined the morphology of these.
Through the analysis of X-rays get the thickness of each sample with its corresponding deposition rate. The analysis of X-rays also revealed that nanofilms are not crystalline, showing
the amorphous character of the samples. The results obtained by the technique, atomic force
microscopy (AFM) agree with those obtained using the technique of X-rays. Characterization
by Raman spectroscopy revealed the existence of active modes characteristic of AlN in the
samples.
Keywords: Sputtering, nanofilms, aluminum nitride.
vi
Sumário
Resumo
iv
Abstract
v
Lista de Figuras
viii
Lista de Tabelas
xi
1
Abordagem Teórica do Sputtering
1
1.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.2
Técnicas de Deposição de Filmes Nanométricos . . . . . . . . . . . . . . . . .
2
1.2.1
Deposição Química de Vapor (CVD) . . . . . . . . . . . . . . . . . .
3
1.2.2
Deposição Física de Vapor (PVD) . . . . . . . . . . . . . . . . . . . .
4
1.2.3
Sputtering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
Introdução a Física do Sputtering e Plasma . . . . . . . . . . . . . . . . . . . .
6
1.3.1
A Física do Sputtering . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.3.2
Rendimento em Função da Energia do Íon Incidente . . . . . . . . . .
8
1.3.3
Rendimento em Função da Dependência Angular . . . . . . . . . . . .
9
1.3.4
Plasma . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
Comportamento da Voltagem em Função da Corrente . . . . . . . . . . . . . .
11
1.4.1
Descarga Townsend . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.4.2
Descarga Normal e Abnormal . . . . . . . . . . . . . . . . . . . . . .
13
1.4.3
Região da Descarga Abnormal . . . . . . . . . . . . . . . . . . . . . .
13
1.5
Magnetron Sputtering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
1.6
Sputtering de Rádio-frequência . . . . . . . . . . . . . . . . . . . . . . . . . .
17
1.7
Deposição e Nucleação de Filmes . . . . . . . . . . . . . . . . . . . . . . . .
17
1.3
1.4
2
Materiais e Métodos
20
2.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
2.2
O Alumínio (Al) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
2.3
O Nitrogênio (N) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.4
O Nitreto de Alumínio (AlN) . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
2.5
Mecanismo de Deposição . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
SUMÁRIO
2.5.1
2.6
3
O Sistema Rapier/Orion AJA . . . . . . . . . . . . . . . . . . . . . . .
27
Preparação dos Nanofilmes de AlN . . . . . . . . . . . . . . . . . . . . . . . .
32
Técnicas de Caracterização dos Filmes
33
3.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
3.2
Difração de Raios-X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
3.2.1
Contextualização Histórica . . . . . . . . . . . . . . . . . . . . . . . .
34
3.2.2
Geração e emissão de Raios-X . . . . . . . . . . . . . . . . . . . . . .
36
3.2.3
Equação de Bragg para Difração . . . . . . . . . . . . . . . . . . . . .
39
3.2.4
Difração de Raios-X . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
Espectroscopia Raman . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
3.3.1
Contextualização Histórica . . . . . . . . . . . . . . . . . . . . . . . .
43
3.3.2
Espectroscopia Ótica . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
3.3.3
As Regiões do Espectro Eletromagnético . . . . . . . . . . . . . . . .
45
3.3.4
O Efeito Ramam . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
3.3.5
A Espectroscopia Raman . . . . . . . . . . . . . . . . . . . . . . . . .
50
3.3.6
Vibrações em Sólidos Cristalinos . . . . . . . . . . . . . . . . . . . .
53
Microscopia de Força atômica (AFM) . . . . . . . . . . . . . . . . . . . . . .
54
3.3
3.4
4
vii
Resultados
56
4.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
4.2
Difração por Raios-X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
4.2.1
Difratogramas da Alvo . . . . . . . . . . . . . . . . . . . . . . . . . .
56
4.2.2
Parâmetros de deposição . . . . . . . . . . . . . . . . . . . . . . . . .
59
4.2.3
Difratogramas dos Nanofilmes . . . . . . . . . . . . . . . . . . . . . .
60
4.2.4
Difratogramas dos Nanofilmes a Baixos Ângulos . . . . . . . . . . . .
61
4.3
Microscopia de Força Atômica (AFM) . . . . . . . . . . . . . . . . . . . . . .
64
4.4
Espectroscopia Raman . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
4.4.1
Espectro Raman do Alvo e Modos de Vibração . . . . . . . . . . . . .
65
4.4.2
Espectro Raman das Amostras AlN . . . . . . . . . . . . . . . . . . .
67
Considerações Finais e Perspectivas
69
A Tabela Periódica
70
Referências Bibliográficas
72
viii
Lista de Figuras
1
The scientist . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1
Esquema do aparato utilizado por Grove em 1852. Identificamos na ilustração
iii
a bateria A, um transformador B e a câmara evacuada onde ocorria a deposição
C [4]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2
2
Fenômenos que ocorrem durante a interação entre os íons incidentes e a superfície do alvo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.3
Esquema de sputtering DC [10]. . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.4
Rendimento sputtering para o cobre em função das energias dos íons de gases
nobres [4]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5
Dependência do rendimento do sputtering em função do ângulo de incidência
do íon em relação a normal à superfície do alvo [5]. . . . . . . . . . . . . . . .
1.6
9
9
Lâmpada de plasma, essencialmente constituída por uma esfera de vidro com
gás a baixa pressão e um eletrodo central a alta voltagem. As cores são resultado
do decaimento dos elétrons excitados para níveis mais baixos de energia, depois
de terem se recombinado com os íons. Nesse processo, há emissão de luz no
espectro característico do gás que está sendo excitado [14]. . . . . . . . . . . .
1.7
10
Plasma de argônio no interior da máquina de plasma quiescente do LAP. Ímãs
permanentes são colocados em volta da parede interna da câmara de vácuo,
produzindo um campo magnético de confinamento por cúspides multipolares.
Pode-se ver claramente que os elétrons de alta energia seguem as linhas de
campo magnético. O objeto fino e escuro no meio do plasma é uma sonda
eletrostática [15]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.8
Plasma obtido durante a deposição dos nanofilmes de AlN apresentados nesse
trabalho. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.9
10
12
Curva voltagem-corrente para uma descarga elétrica em um gás a baixa pressão
[16]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.10 Comportamento luminoso de uma descarga elétrica em gases [1]. . . . . . . . .
13
1.11 Regiões luminescentes do plasma, características de tensão e cargas para uma
descarga DC abnormal [16]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
1.12 Esquema de magnetron sputtering. . . . . . . . . . . . . . . . . . . . . . . . .
15
LISTA DE FIGURAS
ix
1.13 Nucleação e crescimento dos filmes durante a condensação heterogênea [21]. .
18
1.14 Esquema do processo de crescimento de um filme [23]. . . . . . . . . . . . . .
19
2.1
Localização do Alumínio na tabela períodica [26]. . . . . . . . . . . . . . . . .
21
2.2
Localização do nitrogênio na tabela períodica [30]. . . . . . . . . . . . . . . .
23
2.3
Em a) um átomo de Al cercado por quatro átomos de N, formando um tetraedro
distorcido. Em b) a célula unitária do AlN, formando uma estrutura wurtzítica
hexagonal [30]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
2.4
Visão interna da câmara de deposição. . . . . . . . . . . . . . . . . . . . . . .
27
2.5
Equipamento de sputtering Rapier/Orion sputtering system da AJA. . . . . . .
28
2.6
À esquerda, bomba mecânica de baixo vácuo Alcatel Vacuum Technology, série 2005 SD de dois estágios. À direita, bomba turbomolecular de alto vácuo
Pfeiffer Vacuum TMU 071P . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1
29
Equipamentos utilizados por Röntgen. Em (a), o primeiro equipamento de raiox produzido no laboratório de Röntgen, e em (b) os equipamentos originais do
seu laboratório [38]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
3.2
Padrão de difração de raios-X como obtido por Laue e colaboradores [41]. . . .
35
3.3
Espectro de emissão de raios-X produzido quando se utiliza o metal Molibdênio
como alvo numa ampola de raios-X, funcionando a 35kV [43]. . . . . . . . . .
36
3.4
Processo de geração de raios-X no interior de um átomo [42]. . . . . . . . . . .
37
3.5
Localização dos raios-X no espectro eletromagnético [44]. . . . . . . . . . . .
38
3.6
Ilustração do efeito Bremsstrahlung [42]. . . . . . . . . . . . . . . . . . . . .
39
3.7
Esquema de difração dos raios-X [42]. . . . . . . . . . . . . . . . . . . . . . .
40
3.8
Padrão de difração (difratograma) de pó do NaCl [40]. . . . . . . . . . . . . .
41
3.9
Ilustração esquemática de um difratômetro de raios-X, T(fonte), S(amostra),
C(detector) e O(eixo ao redor do qual giram a amostra e o detector) [45]. . . . .
43
3.10 Aparato utilizado por Raman [48]. . . . . . . . . . . . . . . . . . . . . . . . .
44
3.11 Espectro eletromagnético [52]. . . . . . . . . . . . . . . . . . . . . . . . . . .
47
3.12 Diagramas de níveis de eneregia para os efeitos Stokes e anti-Sotkes. . . . . . .
48
3.13 Os efeitos Stokes e anti-Sotkes em um espectro Raman. . . . . . . . . . . . . .
49
3.14 Polarização induzida em uma molécula por campo elétrico. A radiação espalhada pode estar em vários sentidos, na figura são mostrados em 90° e 180º
[57]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
3.15 CCD (charge-coupled device) ou Dispositivo de Carga Acoplada, especialmente
desenvolvido para uso na obtenção de imagens no ultravioleta [58]. . . . . . . .
51
3.16 Diagrama típico de um equipamento necessário para a obtenção de um espectro
Raman [60]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
LISTA DE FIGURAS
x
3.17 Espectro Raman ressonante do vapor de iodo, excitação 514 nm, mostrando a
banda fundamental (215 cm−1 ) e algumas das harmônicas [62]. . . . . . . . . .
53
3.18 Representação esquemática do conjunto haste-sonda-amostra. No detalhe, a
sonda e suas dimensões nanométricas. [68]. . . . . . . . . . . . . . . . . . . .
55
3.19 O potencial de Lennard-Jones. Na área abaixo da linha de força nula, as forças
são atrativas. Acima desta linha, as forças são repulsivas [68]. . . . . . . . . .
4.1
Difratograma do alvo de nitreto de aluminio usado em nossas deposições, onde
os gráficos (a) e (b) indicam os dois lados do nosso alvo. . . . . . . . . . . . .
4.2
55
57
Difratogramas, em (a) pó de nitreto de alumínio comercial [69], em (b) um dos
lados do alvo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
4.3
Difratogramas das amostras depositadas em vidro e silício. . . . . . . . . . . . . . .
60
4.4
Difração de raio-X baixo ângulo para calibração da taxa de deposição. Gráfico
(a) picos a baixo ângulo obtidos para a amostra AlN no vidro a 5 horas, gráfico (b) vetor de espalhamento q versus o índice dos picos de Bragg, ajustado
linearmente. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5
61
Difratogramas a baixos ângulos e ajustes lineares. Onde temos em (a) AlN
sobre silício depositado durante 3 horas e em (b) AlN sobre vidro depositado
durante 5 horas.
4.6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
Difratogramas a baixos ângulos obtidos em Santa Maria, onde temos em (a)
AlN sobre silício depositado durante 3 horas e em (b) AlN sobre vidro depositado durante 5 horas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7
Difratograma a baixo ângulo para o nitreto de alumínio sobre o vidro depositado
durante 10 horas, difratogrma (UFSM-LMMM). . . . . . . . . . . . . . . . . .
4.8
63
63
Espectrômetro T64000 da Jobin Yvon-SPEX, Division d’Instruments S.A. com
seu sistema de micro-análise. . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
Espectro Raman para o nitreto de alumínio puro. . . . . . . . . . . . . . . . .
66
4.10 Espectro Raman para as amostras do nitreto de alumínio. . . . . . . . . . . . .
67
A.1 Tabela Periódica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
70
A.2 Dados Referentes ao Nitreto de Alumínio. . . . . . . . . . . . . . . . . . . . .
71
4.9
xi
Lista de Tabelas
1.1
Rendimento de sputtering para alguns elementos a 500 eV [4]. . . . . . . . . .
1.2
Relação entre pressão e livre caminho médio usando-se magnetron sputtering
[4].
8
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
2.1
Propriedades alumínio [28]. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
2.2
Propriedades nitrogênio [31]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
2.3
Ambientes de vácuo e suas respectivas pressões [1].
29
3.1
Valores aproximados de comprimentos de onda, frequência e energia para algu-
. . . . . . . . . . . . . .
mas regiões do espectro eletromagnético [51]. . . . . . . . . . . . . . . . . . .
46
4.1
Parâmetros envolvidos na deposição dos nanofilmes. . . . . . . . . . . . . . .
59
4.2
Espessuras e taxas de deposições, obtidos por raios-x a baixos ângulos.
64
4.3
Espessuras e taxas de deposições, obtidos por microscopia de força atômica.
4.4
.
64
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
Valores experimentais e
[71].
. . . .
teóricos∗
obtidos para os modos ativos Raman em AlN
1
C APÍTULO 1
Abordagem Teórica do Sputtering
“Toda a nossa ciência, comparada com a realidade, é
primitiva e infantil- e no entanto, é a coisa mais preciosa
que temos.”
—ALBERT EINSTEIN(1879 − 1955)
1.1
Introdução
Muitos materiais empregados em dispositivos eletrônicos são fabricados em forma de filmes
finos (nanofilmes). Os nanofilmes são depositados em um substrato por evaporação térmica, decomposição química, ou evaporação de matérias-primas pela irradiação de espécies energéticas
ou fótons. Os filmes são feitos com metais, isolantes, semicondutores ou supercondutores, dependendo da aplicação desejada. Dentre os vários métodos de obtenção de nanofilmes, os que
usam a técnica de sputtering1 , despertam grande interesse devido às características adquiridas
pelos filmes depositados [1].
O efeito sputtering foi reportado à primeira vez há quase dois séculos atrás. Em 1852, Sir
William Robert Grove (1811 − 1896) apresentou um trabalho que previa a primeira observação
registrada de "sputtering", na "Philosophical Transactions" da Royal Society em Londres [2].
Embora outros pesquisadores tivessem observado o efeito, foi Grove o primeiro a estudar o que
ficou conhecido como “sputtering” enquanto pesquisava descargas luminescentes [3].
Grove observou que havia deposição de um material, quando ligava seu aparato que consistia, aproximadamente, em um circuito formado por uma ponta de fio mantido próximo a uma
superfície altamente polida de prata, que eram seus eletrodos, na presença de gases reagentes
sob uma pressão de 0,5 Torr. Ele observou também o desaparecimento da deposição quando a
1 Como
ainda não há consenso entre os pesquisadores quanto à tradução de algumas palavras de ori-
gem inglesa, elas aparecerão no texto em inglês com caracteres em modo itálico seguidas da sua tradução,
entre parênteses, mais aceita para o português. A palavra supttering, no entanto, será utilizada como tal
no texto em português, pois as traduções “pulverização” e “desbaste”, não guardam o sentido original da
expressão além dessa ser a maneira como ela é utilizada corretamente no meio científico.
1.2 TÉCNICAS DE DEPOSIÇÃO DE FILMES NANOMÉTRICOS
2
polaridade dos eletrodos era invertida [3]. O esquema do aparato utilizado por Grove em 1852
está representado na Figura 1.1.
Figura 1.1 Esquema do aparato utilizado por Grove em 1852. Identificamos na ilustração a bateria A,
um transformador B e a câmara evacuada onde ocorria a deposição C [4].
Neste capítulo discutiremos algumas técnicas de deposição de nanofilmes, os processos de
sputtering, plasma e nucleação.
1.2
Técnicas de Deposição de Filmes Nanométricos
Atualmente há uma enorme variedade de processos para deposição de filmes nanométricos
(espessuras < 100 nm). Essa grande variedade dar-se, não só pelo avanço tecnológico, como
também pela grande aplicabilidade desses compostos, tais como em microeletrônica, óptica e
nanotecnologia.
As tecnologias de deposição dessas nanoestruturas são basicamente agrupadas em puramente físicos tais como os métodos de evaporação, puramente químicos ou métodos físicoquímicos como o sputtering reativo [5].
As técnicas (PVD) Physical Vapour Deposition (deposição física de vapor), e (CVD) Chemical Vapour Deposition (deposição química de vapor), são os métodos mais comuns para a
transferência de materiais, átomo por átomo, de uma ou mais fontes de crescimento de filmes a
serem depositados na superfície de um substrato [6].
Se o material depositado é produto de uma reação química, o processo é classificado como
CDV, se o transporte dos vapores a partir da fonte geradora até o substrato é feito por meios
físicos, sob um ambiente de vácuo, o processo é do tipo PDV.
É importante ressaltar que essas técnicas não competem entre si, mas complementam-se
na tentativa de equilibrar as vantagens e desvantagens de cada uma. Na próxima seção será
descrito de forma resumida as principais características desses métodos.
1.2 TÉCNICAS DE DEPOSIÇÃO DE FILMES NANOMÉTRICOS
1.2.1
3
Deposição Química de Vapor (CVD)
CVD ou deposição química a vapor é uma importante técnica para síntese de nanofilmes.
Com a técnica de CVD é possível fazer deposição de metais, elementos não metálicos e ainda
grande quantidade de compostos como carbonetos, nitretos, óxidos, compostos intermetálicos,
entre outros. Essa tecnologia é fator essencial, por exemplo, para a indústria de semicondutores,
componentes eletrônicos, optoeletrônicos, foto-senssíveis e de revestimentos [7].
De modo geral, a formação de filmes por esse processo pode ser definida pela deposição
atômica ou molecular (ou combinação desses) do filme em uma superfície aquecida, sendo que
o filme depositado é oriundo de uma reação química, onde os precursores (átomos ou moleculas
que formão o filme) estão na fase de vapor [5].
A morfologia do filme depositado é fortemente influenciada pela natureza da reação química
e pelo mecanismo de ativação. Os principais mecanismos de ativação das reações químicas são:
aplicação de luz, calor, campos de radio-frequência, raios-X, arcos voltaicos dentre outros.
Entre as principais vantagens da técnica estão:
• Proporcionam altas taxas de deposição de filme;
• Os equipamentos utilizados para CVD não requerem ultra-vácuo e são bastante versáteis;
• Há possibilidade na mudança de composição durante a deposição e a co-deposição de
elementos ou compostos.
Entretanto, as principais desvantagens são:
• Altas temperaturas são requeridas para manter o processo de forma eficiente;
• Os gases reativos, e os produtos voláteis presentes nos processos são, na maioria dos casos,
altamente tóxicos, explosivos ou corrosivos;
• O controle da uniformidade dos filmes depositados é na maioria das vezes difícil.
1.2 TÉCNICAS DE DEPOSIÇÃO DE FILMES NANOMÉTRICOS
1.2.2
4
Deposição Física de Vapor (PVD)
Nessa técnica, os filmes são depositados num substrato, em unidades atômicas ou moleculares, simplesmente pelo processo da condensação. Por meio de processos físicos, tais como a
evaporação, sublimação ou choque iônico em um alvo, átomos ou moléculas são transferidos
da fonte para o substrato onde se depositam. Sputtering e evaporação são os dois métodos mais
utilizados por essa técnica para depositar filmes. Dentro das técnicas de evaporação podemos
citar a evaporação a vácuo, a electron beam, a molecular beam epitaxy (MBE) [8].
1.2.3
Sputtering
Sputtering é um método de deposição a vácuo, classificado como um método de deposição
via fase de vapor (PVD). Nesse processo, os átomos do material são arrancados da superfície
de um alvo por íons de alta energia gerados por um plasma contido numa câmara a vácuo.
O processo de ejeção do material é conhecido como sputtering, e ocorre como resultado da
transferência de momentum entre os íons incidentes e os átomos do material bombardeado, ver
Figura 1.2. As características mais importantes do processo são:
Figura 1.2 Fenômenos que ocorrem durante a interação entre os íons incidentes e a superfície do alvo.
• O sputtering yield (redimento do sputtring) e as correspondentes taxas de deposição não são
muito diferentes para metais, isolantes e compostos. Isto torna o processo interessante para
deposição de compostos em multicamadas;
1.2 TÉCNICAS DE DEPOSIÇÃO DE FILMES NANOMÉTRICOS
5
• A espessura dos filmes é de modo geral, facilmente controlada. As taxas de deposição são
extremamentes repetitivas, apenas é preciso ajustar o tempo de deposição, mantendo os
demais parâmetros constantes;
• Em deposições tipo sputtering não existe ejeção de grandes aglomerados como acontece,
por exemplo, na evaporção térmica, responsáveis pela falta de uniformidade na espessura
dos filmes;
• Os substratos podem ser limpos antes da deposição por sputtring reverso ou, até mesmo,
sofrerem tratamentos de passivação por plasma. Obturadores podem cobrir os alvos para
processos de limpeza pré-sputtering que visam remover impurezas da superficie do alvo e
também conseguir condições de equílibrio entre o plasma e a temperatura;
• O plasma pode ser manipulado por campos magnéticos para aumentar a taxa de deposição,
melhorar a uniformidade e manter elétrons muito energéticos longe do substrato evitando
maiores aquecimentos;
• Os alvos mesmo com espessuras da ordem de milímetros, são usados para um grande
número de deposições;
• A técnica propicia a deposição de filmes com aderência excepcional.
Existem também desvantagens, uma das principais desvantagens do processo é o desprendimento de muita energia durante sua realização que, de certa forma, é um fator limitante nas taxas
de variação do processo, as taxas de deposição são relativamente baixas, de 5 a 300 nm/mim.
Há também, durante o processo um aquecimento considerável do porta-substrato devido ao
choque continuo de elétrons energéticos. A fim de se evitar o aumento excessivo da temperatura,
costuma-se refrigerar, com água, os eletrodos [1].
Como mencionado no texto acima, existem vários tipos de equipamentos de sputtering que
diferem um do outro, basicamente na forma como se obtêm o plasma. Entre esses equipamentos
que usam o plasma podemos citar, como os mais comuns, o de sputtering convencional ou
do tipo DC (corrente contínua), RF (rádio-frequência), magnetron ou reativo, dependendo da
geometria do sistema alvo-substrato e do modo de transporte dos íons.
6
1.3 INTRODUÇÃO A FÍSICA DO SPUTTERING E PLASMA
1.3
1.3.1
Introdução a Física do Sputtering e Plasma
A Física do Sputtering
Como mencionado na seção precedente, o fenômeno do sputtering encontra-se nas interações entre os íons positivos, gerados por uma descarga elétrica, no gás inerte contido em uma
câmera a baixa pressão. O processo de ejeção do material é o que consiste essencialmente no
fenômeno de sputtering, e ocorre como resultado da transferência de momentum entre os íons
incidentes e os átomos do material atingido. Os átomos ou moléculas ejetados em direções
aleatórias percorrem, inclusive, o espaço existente entre o alvo e o substrato, onde se depositam, formando o filme [9]. Devido aos choques dos íons positivos incidentes no alvo, vários
fenômenos podem ocorrer, dependendo da energia do íon até o momento da colisão, tais como:
• Ao se chocar com o alvo, os íons podem sofrer reflexões, provavelmente sendo neutralizados
no processo;
• O impacto pode gerar a ejeção de elétrons secundários que auxiliam na manutenção da
descarga gasosa (plasma);
• Alguns íons incidentes podem implantar-se no alvo;
• Alguns íons incidentes podem chocar-se com átomos do alvo e através da transferência de
momentum, desencadear uma série de colisões entre os átomos do alvo, levando a ejeção de
alguns desses.
O rendimento do sputtering, ou seja, a eficiência da extração de átomos por íons incidentes
é caracterizada por um parâmetro denominado yield sputtering (Y) (rendimento do sputtering),
sendo denotado pela razão:
Número de átomos ejetados
Número de íons incidentes
Esse processo está relacionado basicamente com:
Y=
• A energia, a natureza e o ângulo de incidência dos íons;
• A massa dos íons incidentes;
• A natureza cristalina e a composição química do material que é constituído o alvo.
(1.1)
1.3 INTRODUÇÃO A FÍSICA DO SPUTTERING E PLASMA
7
Figura 1.3 Esquema de sputtering DC [10].
O rendimento do processo, pode ser expresso em função da energia do íon incidente (E), da
massa atômica dos íons e da massa atômica dos átomos que compõe o alvo [11], como expresso
nas equações 1.2 e 1.3. Estes resultados não possuem um desenvolvimento trivial.
I PARA ÍONS COM ENERGIA E ≤ 1 keV, TEMOS PARA O RENDIMENTO :
Y (E) =
3α mi ma
E
2
2
π (mi + ma ) Uo
(1.2)
Onde:
* Y(E) é o rendimento do sputtering;
* mi é a massa do íon incidente;
* ma é a massa dos átomos do alvo;
* E é a energia cinética dos íons incidentes;
* Uo é a energia das ligações dos átomos do alvo;
* α está relacionada com a razão ma / mi .
I PARA ÍONS COM ENERGIA E > 1 keV, TEMOS PARA O RENDIMENTO :
Y (E) = 3.56α
Zi + Za
2
3
2
3
Zi + Za
mi
Sn (E)
(mi + ma ) Uo
Onde:
* Zi é o número atómico dos íons;
* Za é o número atómico dos átomos que compõem o alvo;
(1.3)
1.3 INTRODUÇÃO A FÍSICA DO SPUTTERING E PLASMA
Elemento
He
Ne
Ar
Kr
Alumínio
0.16
0.73
1.05
0.96 0.82
Silício
0.13
0.48
0.50
0.50 0.42
Titânio
0.07
0.43
0.51
0.48 0.43
Cobre
0.24
1.80
2.35
2.35 2.35
Zircônio
0.02
0.38
0.65
0.51 0.58
8
Xe
Tabela 1.1 Rendimento de sputtering para alguns elementos a 500 eV [4].
* Sn (E) conhecido como stopping power é o valor médio da perda de energia por unidade
de comprimento.
O rendimento é influenciado por vários fatores dependentes tanto do íon quanto do material
bombardeado. A retirada de material do alvo depende da massa do íon incidente, do tipo de
ligação e estrutura do material. Alguns valores de sputtering para íons com energia de 500 eV
para alvos diferentes sobre diferentes atmosferas encontra-se na Tabela 4.1.
Uma rápida análise na Tabela 4.1 fundamenta uma das razões do argônio ser o gás nobre
mais utilizado em atmosferas de sputtering, pois o argônio apresenta rendimento bem maior
que os outros gases, além de possuir um custo menor que o neônio, o cripitônio e o xenônio.
1.3.2
Rendimento em Função da Energia do Íon Incidente
Quanto a variação do rendimento em função da energia do íon incidente, temos que, para
baixos valores de energias do íon incidente, o sputtering terá rendimento nulo, pois essa energia
não será suficiente para romper a energia de ligação dos átomos que constituem o alvo. A
energia de limiar (Et ), específica para cada material, pode ser entendida como a energia cinética
mínima, fornecida aos átomos que formam a rede cristalina do alvo, para que estes possam se
deslocar e, possivelmente, serem ejetados do alvo.
A partir desse valor o rendimento sofre um aumento praticamente exponencial até atingir
um máximo. A partir desse limite máximo o rendimento começa novamente a decrescer como
o aumento da energia, pois devido a colisão ser muito energética os íons se implantam no alvo.
O rendimento depende diretamente da massa dos íons incidentes, como podemos observar na
Figura 1.4 para uma mesma energia, o rendimento do processo cresce com a massa do íon [12].
1.3 INTRODUÇÃO A FÍSICA DO SPUTTERING E PLASMA
9
Figura 1.4 Rendimento sputtering para o cobre em função das energias dos íons de gases nobres [4].
1.3.3
Rendimento em Função da Dependência Angular
Em relação a dependência angular (ângulo de incidência do íon), podemos observar de
acordo com a Figura 1.5, que o rendimento aumenta proporcional ao aumento do ângulo de
incidência dos íons em relação a normal à superfície do alvo . Isso pode ser explicado pelo
fato de que, quanto menor a mudança direcional requerida no momento, mais eficiente será o
choque, resultando na ejeção dos átomos do alvo. Observando a Figura 1.5, temos uma faixa
de máxima eficiência do rendimento entre os ângulos de 45° a 60°, para ângulos maiores, esse
rendimento decresce, favorecendo o fenômeno de reflexão.
Figura 1.5 Dependência do rendimento do sputtering em função do ângulo de incidência do íon em
relação a normal à superfície do alvo [5].
1.3 INTRODUÇÃO A FÍSICA DO SPUTTERING E PLASMA
1.3.4
10
Plasma
Aplicando-se uma diferença de potencial entre dois eletrodos, na presença de um gás a
baixa pressão, obtém-se uma descarga luminosa de corrente contínua. Elétrons originários de
uma emissão termiônica do catodo ou mesmo raios cósmicos, ao atravessarem o campo elétrico
entre os eletrodos darão início ao processo de ionização do gás, gerando o plasma. Além do
fenômeno de ionização, ocorrem outros fenômenos como excitação, relaxação e recombinação
simultaneamente durante o processo de descarga, ver Figuras 1.6 e 1.7. Assim, no caso da
deposição via sputtering, os íons positivos do plasma acelerados pelo campo elétrico, incidem
sobre a superfície do catodo com energia suficiente para a ocorrência de diversos fenômenos,
tais como: aquecimento da superfície do catodo, ejeção de átomos, fótons e elétrons, entre
outros [13].
Esses fenômenos são aproveitados em diversas aplicações da engenharia. O plasma utilizado na maioria das técnicas de engenharia apresenta apenas uma pequena fração de átomos
ionizados, sendo que a grande maioria dos átomos permanecem em estado neutro. Cerca de um
íon para cada 10.000 átomos de gás [4]. Na física, este plasma é denominado plasma frio ou
descarga luminescente.
Figura 1.6 Lâmpada de plasma, essencial-
Figura 1.7 Plasma de argônio no interior da
mente constituída por uma esfera de vidro
máquina de plasma quiescente do LAP. Ímãs
com gás a baixa pressão e um eletrodo cen-
permanentes são colocados em volta da parede
tral a alta voltagem. As cores são resultado do
interna da câmara de vácuo, produzindo um
decaimento dos elétrons excitados para níveis
campo magnético de confinamento por cúspi-
mais baixos de energia, depois de terem se re-
des multipolares. Pode-se ver claramente que
combinado com os íons. Nesse processo, há
os elétrons de alta energia seguem as linhas de
emissão de luz no espectro característico do
campo magnético. O objeto fino e escuro no
gás que está sendo excitado [14].
meio do plasma é uma sonda eletrostática [15].
1.4 COMPORTAMENTO DA VOLTAGEM EM FUNÇÃO DA CORRENTE
11
Em seu volume total, o plasma é eletricamente neutro. Nele coexistem, íons, elétrons e
átomos neutros. Devido a essa composição, o plasma tem um comportamento peculiar quanto
a sua composição de cargas, polaridade e temperatura. Como os íons apresentam massa muito
superior aos elétrons, esses mais leves, respondem melhor a mudanças no campo elétrico, sendo
ditos como portadores efetivos de carga. Desse modo, o plasma tem a capacidade de responder
a mudanças locais de potencial muito rapidamente, sendo quase neutro externamente, mesmo
tendo a capacidade de conduzir energia elétrica.
As cargas presentes tendem a rearranjar o potencial existente no plasma. Deste modo, a
região positiva próximo ao catodo fica concentrada em cargas negativas. Os elétrons se acumulam nesta região para anular o campo elétrico. No restante do espaço, o plasma apresenta uma
diferença de potencial próximo de zero [1].
A voltagem de ruptura é definida como a voltagem mínima necessária para o estabelecimento de uma descarga elétrica, onde tanto a pressão quanto a distância entre os eletrodos
afetam essa voltagem. Para distâncias muito pequenas, ou pressões muito altas, elétrons e íons
não são acelerados o suficiente para provocar ionizações. O processo de ionização começa logo
depois de aplicada a diferença de potencial entre os eletrodos, geralmente utiliza-se algum tipo
de gás nobre para a ionização, sendo o argônio o gás mais utilizado.
Ao colidir com um átomo do gás, o elétron gera um íon e um novo elétron devido ao campo
elétrico. Esse íon é acelerado em direção ao catodo e os dois elétrons em direção ao anodo. Se o
elétron percorrer uma distância suficiente para adquirir energia cinética, por meio da aceleração
do campo, ele poderá mais uma vez ionizar o gás. As reações para formações de ions (Ar+ ) e
espécies excitadas (Ar∗ ) de um átomo de argônio são:
e− + Ar→ Ar+ + 2e−
(1.4)
e− + Ar→ Ar∗ + e−
(1.5)
Assim, devido à aceleração gerada pelo campo elétrico, os íons atingem o catodo e, dependendo de sua energia cinética no choque contra o alvo, podem, nessa colisão, emitir elétrons
secundários entre muitos outros processos. Esses elétrons secundários podem, ser acelerados
na direção do anodo e gerarem novas reações, provocando um efeito em cadeia, estabelecendo
uma descarga estável e mantendo o plasma.
1.4
Comportamento da Voltagem em Função da Corrente
Uma vez estabelecida, a descarga continua a apresentar diferentes estados em função da
tensão, como pode ser observado na Figura 1.9.
1.4 COMPORTAMENTO DA VOLTAGEM EM FUNÇÃO DA CORRENTE
12
Figura 1.8 Plasma obtido durante a deposição dos nanofilmes de AlN apresentados nesse trabalho.
Figura 1.9 Curva voltagem-corrente para uma descarga elétrica em um gás a baixa pressão [16].
1.4.1
Descarga Townsend
Como relatado na seção anterior, quando uma voltagem é aplicada nos terminais da câmara,
flui pelo sistema uma corrente muito pequena devido à presença dos poucos íons e elétrons
gerados por uma variedade de processos. Aumentando-se a voltagem uma energia suficiente é
fornecida aos íons e elétrons constituintes do gás, nesse ponto, principalmente os íons positivos,
iniciam o processo de produção de elétrons secundários devido as colisões com os átomos que
compõe o alvo. Esses elétrons também ionizam o gás através de choques com os átomos neutros
presentes na câmara, produzindo mais elétrons que, por sua vez, produzem mais íons, resultando
numa avalanche de íons e elétrons. Este processo de criação de carga se torna tão efetivo, que
o fluxo de partículas e a corrente aumenta abruptamente, essa região de descarga é denominada
"descarga Townsend".
1.4 COMPORTAMENTO DA VOLTAGEM EM FUNÇÃO DA CORRENTE
1.4.2
13
Descarga Normal e Abnormal
Quando o número de elétrons é suficiente para gerar íons que regenerem o mesmo número
de elétrons, a descarga se auto-sustenta. Nesta fase, ocorre uma queda na voltagem com um
aumento brusco da corrente e da luminescência da descarga gasosa. Assim, a voltagem diminui
até um limiar mínimo, é esta pequena região de voltagem constante e de aumento da intensidade
da corrente, que é denominada região de "descarga normal".
Quando o catodo torna-se totalmente coberto pela luminescência, um aumento na voltagem
aplicada ou aumento na pressão do gás gera um aumento proporcional na corrente. O comportamento do plasma nessa região é ôhmico. Esse regime de descarga é denominado de descarga
"abnormal ou anormal". É essa região que, normalmente, é utilizada no processo de sputtering.
Como também na maioria dos processos que utilizam descarga gasosa, principalmente porque, nela as correntes e voltagens são relativamente altas e toda área do catodo recebe corrente
o que proporciona deposições mais uniformes, ver Figura 1.10.
Figura 1.10 Comportamento luminoso de uma descarga elétrica em gases [1].
Com o aumento da corrente a região abnormal é ultrapassada, esse aumento da corrente
provoca o aparecimento de arcos voltaícos, com uma queda abrupta na voltagem. Esse regime é
caracterizado por uma corrente mais elevada e uma diferença de potencial muito mais baixa que
a descarga na região luminosa. Devido à elevada corrente e o alto fluxo de calor, esse regime
requer cuidados especiais para os eletrodos, esse efeito de aquecimento provocado pela corrente
é amplamente utilizado na engenharia em processos como soldagem.
1.4.3
Região da Descarga Abnormal
A descarga luminescente de corrente contínua também é caracterizada por regiões luminosas e escuras. A Figura 1.11, mostra a arquitetura clássica de uma região de luminosidade DC
1.4 COMPORTAMENTO DA VOLTAGEM EM FUNÇÃO DA CORRENTE
14
constituída de bainha do catodo, espaço escuro do catodo, descarga luminescente negativa, espaço escuro de Faraday e coluna positiva. A bainha catódica é uma faixa luminosa que envolve
toda região próxima ao catodo, nela a radiação é emitida devido aos processos de excitação
e neutralização dos íons juntos a superfície do catodo. Essa região tem densidade de carga
predominantemente negativa, devido a mobilidade dos elétrons e pelo surgimento de elétrons
secundários, oriundos dos choques entre os íons acelerados e o catodo.
A próxima região em frente do catodo é escura, nela está praticamente toda a diferença de
potencial da descarga. Essa região é responsável pela grande aceleração dos íons em direção ao
catodo. Devido a aceleração do campo elétrico os elétrons secundários ganham energia cinética
nessa região, percorrendo uma distância correspondente ao seu livre caminho médio, adquirindo
energia para ionizar os íons dos átomos do gás. Essa região também é conhecida como "espaço
escuro de Crookes".
Figura 1.11 Regiões luminescentes do plasma, características de tensão e cargas para uma descarga DC
abnormal [16].
1.5 MAGNETRON SPUTTERING
15
Logo após o espaço escuro de Crookes, está a região de luminosidade intensa também conhecida como região de luminosidade negativa. Essa região é a mais brilhante de toda descarga.
Nessa região, de brilho intenso, os elétrons perdem praticamente toda sua energia através de
colisões e são acelerados novamente em direção ao anodo. Como consequência, no espaço subseqüente, a descarga luminosa dar lugar a uma nova região escura mais extensa que a anterior,
denominada "espaço escuro de Faraday". Ao percorrerem esse espaço, os elétrons ganham
energia cinética suficiente para novamente gerar colisões ionizantes, dando origem a denominada "coluna positiva". Essa região constituinte do plasma, é uma região passiva e costuma ser
uniforme e longa. Sua função é manter, por meio dos elétrons, a condução da corrente que se
estabelece na região catódica. O tamanho dessa coluna depende do afastamento do catodo ao
anodo. Assim, depois de desacelerados na coluna positiva os elétrons adquirem energia dando
origem a "luminosidade do anodo". No espaço entre a luminosidade do anodo e o próprio anodo
existe uma região conhecida como "espaço escuro do anodo". Vale ressaltar que os plasmas nem
sempre apresentam todas essas regiões tão claramente definidas.
1.5
Magnetron Sputtering
Com o intuito de melhorar a eficiência do plasma foi desenvolvida uma técnica que consiste
em criar um confinamento do elétron na região próxima ao alvo. Em corrente contínua na
região de descarga abnormal, o plasma se distribui através de toda a câmara e muita energia
é desperdiçada. Os elétrons ejetados do alvo muitas vezes seguem trajetórias aleatórias que os
levam às paredes da câmara, assim são poucas as oportunidades de colisão entre um elétron e um
átomo. Essa baixa taxa de ionização implica em uma baixa eficiência energética do plasma [17].
O magnetron Sputtering é uma técnica que emprega ímãs junto à superfície de um alvo gerando
um fluxo incidente de íons sobre sua superfície. Estes íons permitem que uma quantidade muito
maior de átomos ou grupo de átomos seja ejetados da superfície do alvo por transferência de
momentum, ver Figura 1.12.
Figura 1.12 Esquema de magnetron sputtering.
1.5 MAGNETRON SPUTTERING
16
Através da aplicação de campos magnéticos adequados pode-se aumentar, de forma considerável, a eficiência de ionização numa descarga elétrica. Aplicando-se um campo magnético
→
−
→
−
B , numa descarga elétrica, a força F que age sobre um elétron é dada pela resultante devido
as forças elétrica e magnética, como descrito pela equação 1.6.
→
−
→
−
→
−
−
F = q E + (q→
v X B ),
(1.6)
→
− →
−
onde E e B são os campos elétrico e magnético, respectivamente, q é a carga do elétron
→
−
−
−
e→
v é a sua velocidade. O efeito do termo da componente magnética (q→
v X B ) é tornar a
trajetória do elétron espiralada, se comparado a trajetória da partícula sem o campo magnético.
Devido ao aumento do comprimento da trajetória do elétron, aumenta-se a probabilidade de
colisão com as moleculas do gás, elevando o grau de ionização da descarga. Como o módulo
da componente magnética é o mesmo tanto para os elétrons como para átomos monoionizados, a tragetória dos átomos, comparada com a dos elétrons é pouco influenciada pelo campo
magnético.
No magnetron sputtering, o livre caminho médio do gás é grande chegando até 50 cm para
alguns volores de pressão, ver Tabela 1.2. Os elétrons confinados percorrem uma trajetória
maior e, com isso, aumentam a probabilidade de choques com os átomos do gás. A eficiência
do processo de sputtering melhora drasticamente, permitindo, simultaneamente, que a descarga
se realize a pressão mais baixa (10 − 3 Torr ou 0, 13 Pa) e corrente mais alta. O resultado é a
formação de filmes mais densos, puros e com alta qualidade [18].
Pressão (Torr)
Livre Caminho Médio (mm)
10−2
5
10−3
50
10−4
500
10−5
5000
Tabela 1.2 Relação entre pressão e livre caminho médio usando-se magnetron sputtering [4].
1.6 SPUTTERING DE RÁDIO-FREQUÊNCIA
1.6
17
Sputtering de Rádio-frequência
Quando o alvo a ser bombardeado é isolante, a chegada dos íons ao alvo gera um potencial
de blindagem que interrompe a aceleração dos mesmos. Com isso não se tem mais emissão de
elétrons secundários, sendo impossível a auto-sustentação do plasma.
Para sustentar o plasma, quando o alvo é um isolante, a fonte de alimentação de tensão
continua é substituída por uma fonte de tensão alternada. Este sistema é chamado de sputtering
RF ( radio-frequência).
No sputtering RF, utiliza-se uma fonte de corrente alternada e altas freqüências de 13 a
50 MHz. A descarga gasosa presente na câmara quando se usa esta técnica é semelhante à
descarga de corrente contínua, porém com espaços escuros alternando-se nos eletrodos com a
freqüência da descarga. O processo de deposição dos nanofilmes torna-se mais eficiente, pois
os elétrons adquirem mais energia quando oscilam no campo da radio-freqüência. Isto também
possibilita a operação do sistema a pressões mais baixas se comparado com outras modalidades
de sputtering.
No sputtering RF, há quase inexistência de arcos unipolares comuns em sputtering convencional devido ao fato de, no processo, a alternância proporcionada pela fonte inverter a direção
do campo elétrico duas vezes por ciclo dificultando a sustentação do arco. O alvo do sistema
é bombardeado alternadamente tanto por elétrons como por íons evitando-se acumulo de cargas, uma vez que as cargas positivas acumuladas durante um meio ciclo são neutralizadas por
elétrons no meio ciclo seguinte. Num ciclo de radio-frequência a transferência total de cargas é
nula.
Outra grande vantagem dessa técnica, é que ela permite a deposição de filmes conservandose a estequiometria a partir de alvos isolantes e/ou refratários o que é muito difícil de obter por
outros métodos [19].
1.7
Deposição e Nucleação de Filmes
Os nanofilmes são formados por condensação dos átomos ou moléculas de um vapor sobre
o substrato. A estrutura do substrato influência fortemente as propriedades do filme depositado
durante a nucleação, na fase de crescimento do filme. O mecanismo de fixação é denominado
adsorção física, e ocorre quando não há transferências de elétrons entre o material que compõe
o substrato e as partículas ou moléculas depositadas nele. A energia de ligação associada à
adsorção física é de aproximadamente 0, 25 eV.
1.7 DEPOSIÇÃO E NUCLEAÇÃO DE FILMES
18
Na deposição, os filmes são formados átomo a átomo, sendo que as forças responsáveis
pela fixação dos átomos na superfície do substrato têm origem eletrostática. Ao atingir a superfície do alvo, os íons energéticos, causam além da ejeção de átomos da superfície do alvo,
fenômenos tais como, retro-espalhamento de elétrons, emissão de raios-X, geração de fótons,
emissão de elétrons secundários dentre outros. Os átomos de vapor do material ejetado do alvo
são adsorvidos no substrato, mas ainda não estão combinados com outros átomos adsorvidos
[20].
O processo de condensação se inicia nos primeiros momentos de formação do filme, pela
formação de pequenos clustres (aglomerados), resultantes da combinação de vários átomos
adsorvidos. Esses aglomerados são denominados nucleídeos e seu processo de formação é
denominado nucleação. Crescimento é o processo de expansão dos núcleos, originando de
forma coerente o filme, frequentemente, nucleação e crescimento ocorrem simultaneamente
durante a formação do filme.
A Figura 1.13, mostra um nanofilme que cresce a partir da aglutinação dos átomos que
chegam à superfície do substrato (B, C), formando os nucleídeos (D). Estes estão se formando
quando átomos do alvo ou do gás bombardeiam a superfície do alvo.
Figura 1.13 Nucleação e crescimento dos filmes durante a condensação heterogênea [21].
Os átomos incidentes têm capacidade de partir ou desintegrar os nucleídeos (E). No entanto,
os nucleídeos ou suas regiões mais estáveis permanecem no substrato. Com a chegada de novas
partículas na superfície, os nucleídeos coalescem e se unem a outros nucleídeos.
De acordo com a Figura 1.14, podemos entender de modo simplificado a formação do filme,
começando pela nucleação, seguida pelo fenômeno de coalescência, que é a fusão das pequenas ilhas em entidades maiores, até o ponto que finalmente todos os buracos do material são
preenchidos, formando o filme contínuo [22].
As características finais do filme, assim como sua reprodutibilidade, dependem do conhecimento e do controle de vários parâmetros e fatores durante todo o processo de seu crescimento.
1.7 DEPOSIÇÃO E NUCLEAÇÃO DE FILMES
19
Figura 1.14 Esquema do processo de crescimento de um filme [23].
E muito difícil e complexo controlar a influência de todos esses fatores, uma vez que eles agem
de modo simultâneo.
20
C APÍTULO 2
Materiais e Métodos
“A vida sem ciência é uma espécie de morte.”
—SÓCRATES (470 a.C. - 399 a.C.)
2.1
Introdução
No presente capítulo, iremos descrever os materiais e métodos usados na produção dos
nossos nanofilmes de nitreto de alumínio. Começaremos a nossa discussão com os elementos
químicos alumínio e nitrogênio, suas propriedades fundamentais, síntese e algumas curiosidades pertinentes. Em seguida, falaremos sobre o nitreto de alumínio (AlN) e dos nanofilmes
de nitreto de alumínio, algumas características e sua grande importância em aplicações tecnológicas atuais. Dando seguimento, descreveremos o equipamento usado no crescimento dos
nanofilmes e seus constituintes básicos, tais como, bomba de vácuo, sistemas de refrigeração
e de aquecimento, tudo de forma rápida e sucinta. Por fim, descreveremos o processo de crescimento dos nanofilmes de nitreto de alumínio através do método magnetron sputtering RF e
todos os procedimentos adotados na deposição.
2.2
O Alumínio (Al)
Geralmente é creditado ao químico alemão Friedrich Wöhler (1800 − 1882), o reconhe-
cimento do isolamento do alumínio através da mistura de cloreto de alumínio com potássio
em 1827, embora este metal tenha sido obtido impuro alguns anos antes pelo físico e químico
dinamarquês Hans Christian Oersted (1777 − 1851) [24].
O alumínio, símbolo (Al) é um metal representado no grupo (família) 13 (antigo III-A) e no
terceiro período (série) da tabela periódica1 com número atômico 13, eletronegatividade 1, 61
na escala de Pauling e 3 elétrons no nível mais externo (camada de valência), ver Figura 2.1.
O alumínio é um metal leve, macio e resistente. Possui um aspecto cinza prateado-fosco e é
1 ver
tabela períodica completa no apêndice A.
21
2.2 O ALUMÍNIO (AL)
resistente à corrosão, porque sua superfície é apassivada no ar pela formação de um filme de
óxido estável, a alumina (Al2 O3 ). A espessura da camada de alumina pode ser aumentada,
fazendo o alumínio servir de anodo em uma célula eletrolítica [25].
Figura 2.1 Localização do Alumínio na tabela períodica [26].
Sua leveza, condutividade elétrica, resistência à corrosão e baixo ponto de fusão lhe conferem uma multiplicidade de aplicações, especialmente em soluções de engenharia aeronáutica.
O alumínio em sua forma metálica é não tóxico, não magnético, e não cria faíscas quando exposto ao atrito. Na temperatura ambiente é sólido, sendo um dos elementos mais abundantes
da crosta terrestre, cerca de 8, 1%, porém raramente é encontrado puro na natureza. Alguns
minerais que o contêm são bauxita (hidróxidos de alumínio com argilas), criolita (fluoreto de
alumínio e sódio) e granitos [27]. A Tabela 2.1 lista algumas propriedades do alumínio.
Grandeza
Valor
Unidade
Massa específica do sólido
2700
kg/m3
Ponto de fusão
660.3
°C
Calor de fusão
10.7
kJ/mol
Ponto de ebulição
2519
°C
Calor de vaporização
294
kJ/mol
Eletronegatividade
1.61
Pauling
Estados de oxidação
+3
-
Resistividade elétrica
2.65
10−8 Ω
Condutividade térmica
237
W/(m °C)
Calor específico
904
J/(mol ºC)
Coeficiente de expansão térmica
2.31
10−5 (1/ºC)
Tabela 2.1 Propriedades alumínio [28].
m
2.2 O ALUMÍNIO (AL)
22
A obtenção do metal alumínio foi um desafio para os primeiros cientistas e engenheiros. Ao
ser isolado, o alumínio era um metal raro e caro. Durante o século XIX, simbolizava a tecnologia moderna, era usado como metal precioso em joalheria e até o monumento de Washington
recebeu uma caríssima ponta de alumínio. Toda essa raridade e o alto preço foram transformados pela eletroquímica. O metal alumínio agora é obtido em larga escala pelo processo Hall
[25]. No século XIX, Charles Martin Hall (1863-1914) era estudante de graduação em Oberlin
College, quando um dos seus professores de química o incentivou a tentar encontrar um método para produção de alumínio que fosse prático para o emprego em escala industrial. Hall
teve o pressentimento que a eletrólise deveria servir e, embora nada soubesse de potenciais de
eletrodo padrão ou mesmo da existência de íons (ainda não se sabia da existência dos mesmos),
ele conhecia o trabalho de Faraday sobre a eletrólise. Após algumas tentativas, Hall descobriu
que a alumina (Al2 O3 ) dissolvida em criolita (Na3 AlF6 ), um minério encontrado na Groelândia
que parece gelo, mas se funde a 950°C, servia a seus propósitos [25] [27].
Em 1886, menos de um ano depois de formado, em uma espécie de laboratório num barracão nos fundo de sua casa, Hall finalmente conseguiu alguns glóbulos brilhantes de alumínio2 .
Mesmo com o baixo custo para a sua reciclagem, o que aumenta sua vida útil e a estabilidade do
seu valor, as elevadas quantidades de energia necessária para a obtenção do alumínio, reduzem
sobremaneira o seu campo de aplicação, além das implicações negativas no rejeito dos subprodutos do processo de reciclagem, a produção de uma tonelada de alumínio é acompanhada pela
liberação de mais de uma tonelada de dióxido de carbono na atmosfera [27].
2 Por
coincidência, o mesmo processo foi descoberto uma semana depois por Paul Héroult(1863-1914) na
França. Na Europa é o processo usualmente conhecido como processo Héroult.
2.3 O NITROGÊNIO (N)
2.3
23
O Nitrogênio (N)
Sua descoberta e isolamento são atribuídos ao químico e físico escocês Daniel Rutherford
(1749 − 1819) em 1772. Ele removeu o oxigênio e o dióxido de carbono do ar e verificou que,
no gás residual, não havia combustão. O nome desse elemento provém do grego e significa
"formador de nitron", onde "nitron"se refere ao nitrato de potássio, KNO3 . Em francês, o nome
para nitrogênio é "azoto", que significa "sem vida". O primeiro químico francês A. L. Lavoisier
observou que um rato morreu quando mantido numa atmosfera de nitrogênio [27].
O nitrogênio, símbolo (N) é um ametal representado no grupo (família)15 (antigo V-A) e no
segundo período (série) da tabela periódica, com número atômico 7. Tem uma elevada eletronegatividade, 3 na escala de Pauling, e 5 elétrons no nível mais externo (camada de valência)
comportando-se na maioria dos compostos que forma como um íon trivalente, [29] ver Figura
2.2. É o elemento mais abundante da atmosfera terrestre e está presente em todos os seres
vivos. Nas condições ambientes (25°C e 1 atm) é encontrado no estado gasoso, obrigatoriamente em sua forma molecular biatômica (N2 ) como um gás inerte, incolor, inodoro e insípido,
constituindo 78, 084% da atmosfera terrestre em volume e 75, 5% em peso, não participando da
combustão e nem da respiração [25].
Figura 2.2 Localização do nitrogênio na tabela períodica [30].
A Tabela 2.2 lista as principais propriedades do nitrogênio. O gás nitrogênio puro é obtido
pela destilação fracionada do ar líquido. O ar é resfriado à −196°C pela repetida expansão e
compressão em um refrigerador, através do efeito Joule-Thomson que é o processo no qual a
temperatura de um sistema diminui ou aumenta quando o sistema se expande livremente mantendo a entalpía constante. O efeito Joule-Thomson é usado em alguns tipos de refrigeradores
comerciais para liquefazer gases. O gás a ser liquefeito é comprimido e depois sofre expansão
ao passar por um orifício pequeno, chamado de regulador. O gás esfria quando se expande e o
gás esfriado circula pelo gás comprimido que entra no refrigerador. Esse contato esfria o gás
24
2.3 O NITROGÊNIO (N)
que entra antes que ele se expanda. Como o gás é comprimido continuamente, sua temperatura
cai progressivamente até que finalmente ele se condensa. Se o gás é uma mistura, como o ar,
então o líquido que se forma pode ser destilado posteriormente para a separação de seus componentes. Essa técnica é usada para obter nitrogênio, oxigênio, argônio, criptônio e xenônio da
atmosfera.
Grandeza
Valor
Unidade
28.0134
g/mol
Massa específica do gás (15ºC e 1 atm)
1.185
kg/m3
Ponto de fusão
-210
°C
Calor de fusão
0.72
kJ/mol
-195.8
°C
5.58
kJ/mol
Temperatura crítica
-146.9
°C
Pressão crítica
3399.9
kPa
Massa específica crítica
314.03
kg/m3
Temperatura do ponto tríplice
-210.1
°C
Pressão do ponto tríplice
12.53
kPa
Cp (a 1 atm e 25ºC)
0.029
kJ/(mol ºC)
Cv (a 1 atm e 25ºC)
0.02
kJ/(mol ºC)
Condutividade térmica (a 0ºC e 1 atm)
0.024
W/(m °C)
Solubilidade em água (a 0ºC e 1 atm)
0.0234
vol/vol
3.04
pauling
+5,+4,+3,+2,-3
-
Massa molecular
Ponto de ebulição
Calor de vaporização
Eletronegatividade
Estados de oxidação
Tabela 2.2 Propriedades nitrogênio [31].
Por ser elemento natural da atmosfera, o nitrogênio gasoso não é, a princípio, nocivo, mas
a concentração acidental em ambientes fechados reduz o teor de oxigênio, podendo provocar
asfixia e morte. O ciclo do nitrogênio é um dos processos mais importantes para os seres vivos.
Embora o gás seja relativamente inerte, bactérias no solo são capazes de fixar o nitrogênio na
forma de fertilizantes para as plantas. Animais que as comem, incorporam o nitrogênio como
componente de proteínas. O ciclo se completa quando outras bactérias convertem os compostos
de nitrogênio usados em gás [27].
2.4 O NITRETO DE ALUMÍNIO (ALN)
2.4
25
O Nitreto de Alumínio (AlN)
Os nitretos do grupo III-V têm atraído muita atenção recemtemente devido as suas propriedades físicas que os tornam viáveis em aplicações tecnológicas. Estes nitretos, o GaN (nitreto
de gálio), AlN (nitreto de alumínio) e o InN (nitreto de índio) possuem largura de banda proibida
(band gap) desde 1, 9 eV para o InN, 3, 4 eV para o GaN, até 6, 2 eV para o AlN [32].
O nitreto de alumínio foi sintetizado pela primeira vez em 1907, porém esse composto ficou quase que esquecido por algum tempo. Atualmente o nitreto de alumínio é exaustivamente
estudado devido suas propriedades e várias aplicações principalmente na indústria da microeletrônica. Os elementos químicos nitrogênio e alumínio unem-se através de ligações covalentes
originando o composto nitreto de alumínio. O nitreto de alumínio é um composto químico cerâmico, que tem geralmente simetria wurtzítica hexagonal [33], porém como os outros nitretos
semicondutores (III-N), pode também ser encontrado em mais duas formas cristalinas, a Zincblende e a cúbica (Rocksalt). Em temperatura ambiente o AlN é encontrado na fase estrutural
wurtzítica. Na forma zincblende e na forma cúbica é observado apenas em altas pressões. Estas
duas últimas fases são metaestáveis. A estrutura cristalina do AlN é constituída de um átomo
de alumínio cercado por quatro átomos de nitrogênio, formando um tetraedro distorcido, ver
Figura 2.3. A alta estabilidade química, vem em parte, dos altos valores das duas principais
ligações deste composto, Al-N e Al-Al, cujo os valores são respectivamente, 300 kJmol−1 e 186
kJmol−1 .
Figura 2.3 Em a) um átomo de Al cercado por quatro átomos de N, formando um tetraedro distorcido.
Em b) a célula unitária do AlN, formando uma estrutura wurtzítica hexagonal [30].
2.4 O NITRETO DE ALUMÍNIO (ALN)
26
O nitreto de alumínio é um material cerâmico que não ocorre na natureza, mas pode ser
sintetizado por reações em altas temperaturas, onde se destacam principalmente as técnicas de
deposição química em fase gasosa assistida por plasma reativo, redução carbotérmica e nitretação direta [34]. Devido a sua elevada condutividade térmica (uma das mais altas entre os
materiais semicondutores), o nitreto de alumínio tem se mostrado um material promissor para
uso como substrato de dispositivos eletrônicos de alta potência. Outra característica importante
do AlN é seu alto ponto de fusão, T= 3.487K, calor específico C p = 0, 728 J/gK e temperatura
de Debye θD = 988 K, em sua fase wurtzítica.
A produção de nanofilmes de nitreto de alumínio é recente, os primeiros trabalhos começaram por volta da década de cinqüenta e despertaram grande interesse científico devido as suas
propriedades físico-químicas, cujo resultados apontam os nanofilmes de AlN como um material
altamente promissor em várias aplicações elétricas, ópticas e mecânicas. Os filmes finos (nanofilmes) de AlN, podem ser obtidos por uma grande variedade de técnicas, tanto por epitaxia
como por deposição.
O método sputtering é o mais comumente usado para a obtenção de nanofilmes, tanto por
sua simplicidade e baixo custo, quanto por sua capacidade de obtenção de filmes de boa qualidade e com propriedades desejadas. Na literatura sobre esse material, encontram-se trabalhos
onde as técnicas de deposição variam um pouco em cada trabalho, alguns conseguem melhor
grau de cristalinidade, por exemplo, aquecendo o substrato, enquanto outros usam ambientes de
N2 em baixas pressões [35].
Como o nitreto de alumínio pertence ao grupo III-V da tabela periódica, é um semicondutor
com uma grande largura de banda óptico "bandgap", o que o torna um candidato promissor para
aplicações em dispositivos de alta freqüência, filtros de onda acústica de superfície (SAW), dispositivos ópticos e camadas isolantes. Os valores característicos dessas propriedades dependem
do método e das condições de deposição do filme, sendo que os nanofilmes de AlN podem ser
obtidos tanto por sputtering DC (corrente contínua) como por sputtering RF (rádio frequência)
[37].
Dentre as principais propriedades características dos nanofilmes de nitreto de alumínio, podemos ressaltar, seu elevado valor de dureza e condutividade térmica, e a alta resistência à
temperatura mesmo em ambientes hostis [36]. Abaixo algumas propriedades do AlN e suas
possíveis aplicações:
I Devido a alta condutividade térmica (150 W/mK) e seu baixo coeficiente de expansão
térmica, é possível seu emprego em dispositivos que exigem alta dissipação térmica.
I Em dispositivos acústicos de altas freqüências, devido a sua excelente piezoeletricidade
quando combinada com substratos de alta velocidade, como por exemplo o diamante.
2.5 MECANISMO DE DEPOSIÇÃO
27
I Devido a alta dureza, estabilidade química, elevado ponto de fusão, alta velocidade
acústica, é possível o seu uso em dispositivos que operam sob condições extremas como
sensores para altas temperaturas e pressões.
I Como dispositivos óptico-eletrônicos, quando adequadamente dopado e como janela
transmissora de luz na região espectral na faixa do ultravioleta devido ao seu "bandgap"
direto de 6, 2 eV [35][36][37].
2.5
Mecanismo de Deposição
2.5.1
O Sistema Rapier/Orion AJA
Os nanofilmes de nitreto de alumínio analisados nesse trabalho, foram crescidos pelo método sputtering RF (rádio-frequência), usando o equipamento comercial "Rapier/Orion sputtering system da AJA"do grupo de magnetismo do departamento de física teórica e experimental da Universidade Federal do Rio Grande do Norte (UFRN-DFTE). O equipamento mede
1.75m de altura, ver Figura 2.5, e possui uma câmara para deposição que consiste basicamente
numa câmara de aço inox de formato cúbico com 30 cm aresta. Na parte superior da câmara,
encontram-se dois canhões de duas polegadas cada, e na parte inferior um porta-substrato fixo a
uma distancia de 10 cm do alvo, ver Figura2.4. O porta-substrato é composto por um aquecedor
resistivo, SHQ 15A PID (Proportional Integral Diferential da AJA), que permite o aquecimento
do substrato a uma temperatura de até 900° C. O equipamento para fabricação dos nanofilmes, Rapier/Orion sputtering system é alimentado por uma fonte RF (rádio-frequência), AJA
100/300 MM3X, durante todo o processo de deposição.
Figura 2.4 Visão interna da câmara de deposição.
2.5 MECANISMO DE DEPOSIÇÃO
Figura 2.5 Equipamento de sputtering Rapier/Orion sputtering system da AJA.
28
2.5 MECANISMO DE DEPOSIÇÃO
29
I B OMBAS DE VÁCUO
A câmara de deposição está conectada a duas bombas de vácuo. Antes do início do processo
de deposição, a câmara tem que ser evacuada durante algumas horas até que o regime de alto
vácuo seja atingido. Em geral, para atingir alto vácuo, usam-se duas bombas ligadas em série,
uma de pré-vácuo para a evacuação da câmara até a região de médio vácuo, ligada a outra
bomba onde se alcança alto vácuo. Na tabela 2.3, podemos observar alguns ambientes de vácuo
e suas respectivas pressões. A faixa de pressão do nosso sistema a vácuo é da ordem de 10−6
Torr.
Vácuo Primário
0.1 à 760 Torr ou 10 à 105 Pa
Vácuo Secundário
10−4 à 10−1 Torr ou 102 à 10 Pa
Alto Vácuo
10−8 à 10−4 Torr ou 102 à 10 Pa
Ultra Alto Vácuo
< 10−8 Torr ou < 107 Pa
Tabela 2.3 Ambientes de vácuo e suas respectivas pressões [1].
Em nosso caso, temos uma bomba mecânica de baixo vácuo Alcatel Vacuum Technology,
série 2005 SD de dois estágios, ligada em série a bomba turbomolecular de alto vácuo Pfeiffer
Vacuum TMU 071P, ver Figura 2.6.
Figura 2.6 À esquerda, bomba mecânica de baixo vácuo Alcatel Vacuum Technology, série 2005 SD de
dois estágios. À direita, bomba turbomolecular de alto vácuo Pfeiffer Vacuum TMU 071P
2.5 MECANISMO DE DEPOSIÇÃO
30
I S ISTEMA DE R EFRIGERAÇÃO
Durante todo o processo de deposição dos filmes há aquecimento do equipamento por
vários motivos. Os componentes que apresentam maior tendência ao aquecimento são a bomba
de vácuo termomolecular, o porta-alvo e o porta substrato que se aquecem devido aos choques dos átomos e partículas carregadas no interior da câmara de deposição. A fim de evitar o
superaquecimento é preciso resfriar o sistema para evitar possíveis danos ao equipamento. O
equipamento está ligado a um sistema de refrigeração simples composto basicamente por um
refrigerador fabricado pela empresa Tamisa com capacidade para 160 litros, uma bomba d’água
de alta pressão, necessária para que ocorra circulação da água entre as partes frias e quentes
do sistema, termômetro para monitoramento da temperatura da água em circulação, manômetro e um filtro de água fabricado pela empresa aqua-pure modelo AP055. O resfriamento do
nosso equipamento é feito através da troca de calor entre alguns componentes do equipamento
e o refrigerador, usando-se como meio para equilíbrio térmico a água que circula entre essas
partes do sistema. A água utilizada no processo é água destilada produzida no departamento de
química da UFRN. Todo o sistema de resfriamento do equipamento é automático, basta apenas
selecionar a temperatura de operação do equipamento (-3°C) através de um termostato.
I S ISTEMA DE AQUECIMENTO DO S UBSTRATO
Acoplado ao porta substrato temos um aquecedor resistivo SHQ 15A PID (Proportional
Integral Diferential heat controller) da AJA, responsável pelo aquecimento do substrato a uma
temperatura desejada. A temperatura máxima atingida em nosso sistema é de 900°C.
O controlador PID é a ferramenta responsável pelo controle da temperatura de operação do
equipamento, conferindo precisão e estabilidade durante o processo. O controlador PID pode
ajustar os processos de medidas baseando-se na historia e na taxa de mudança do sinal de erro,
para dar um controle mais apurador e estável da temperatura.
O controlador pode ser entendido como um dispositivo que realiza determinadas operações
matemáticas sobre o sinal de erro, a fim de produzir um sinal a ser aplicado com o intuito de
satisfazer um determinado objetivo. Estas operações matemáticas constituem o que chamamos
de ações de controle. Neste sentido podemos identificar três ações básicas de controle, as ações
proporcional, integral e derivativa. As combinações dessas ações geram um só sinal de controle,
dando origem ao controlador proporcional-integral-derivativo ou simplesmente PID. O objetivo
é aproveitar as características particulares de cada uma destas ações obtendo-se uma melhora
significativa do comportamento transitório e em regime permanente do sistema controlado. Temos que:
2.5 MECANISMO DE DEPOSIÇÃO
31
• P ( proporcional): Correção proporcional ao erro. Correção aplicada ao processo
que deve crescer na mesma proporção que cresce o erro entre o valor real e o desejado.
• I (integral): Correção proporcional ao erro x tempo. Erros pequenos, mas que existem há
muito tempo, requerem correção mais intensa.
• D (derivativa): Correção proporcional à taxa de variação do erro. Se o erro está variando
muito rápido, esta taxa de variação deve ser reduzida para evitar oscilações.
De forma simplificada, temos que esse tipo de controlador trabalha para manter a saída a
um menor nível possível de diferença (erro) entre a variável de processo (pv) e a variável se
seleção [1]. Onde temos:
• A variável de seleção (sv): é o valor aplicado no controlador, o qual define o valor
desejavél pelo usuário para a variável de processo.
• A variável de processo (pv): vem do processo e é enviada ao controlador para comparação
com o valor desejado (sv).
• A variável de controle (cv): sai do controlador e é aplicada no processo para ajustar o
parâmetro que se deseja controlar, cujo o resultado será dado pela variável do processo.
O princípio básico do controlador é:
vp − vs = erro
Se o erro for nulo ou constante ele permanece como resultado. Caso contrário, significa
uma alteração no processo, de modo que o controlador deverá fornecer valores para a variável
de controle de forma a tornar o erro nulo. Assim, o controlador PID ajusta as medidas baseado
na história e na taxa de variação do sinal do erro, conferindo maior controle e estabilidade à
temperatura.
2.6 PREPARAÇÃO DOS NANOFILMES DE ALN
2.6
32
Preparação dos Nanofilmes de AlN
Os nanofilmes de nitreto de alumínio, nesse trabalho, foram crescidos usando o método
magnetron sputtering RF não reativo obedecendo os seguintes procedimentos para o crescimento. Através do sputtering não reativo, crescemos o filme sobre quatro laminas de vidro que
são nossos substratos. Antes de começar a deposição, ligamos o sistema de refrigeração um ou
dois dias antes para que aja acumulo de gelo, pois, como citado nas seções precedentes, uma
temperatura elevada pode acarretará danos ao equipamento. O próximo passo consiste na limpeza do substrato, de modo que, pegamos as laminas de vidro e silício, colocamos num béquer
contendo acetona e levamos ao ultrason durante 10 minutos. Em seguida, repetimos o procedimento citado só que substituindo a acetona por álcool metílico (metanol). Após a limpeza,
depositarmos os substratos na câmara e iniciamos o seu processo de evacuação.
Para fazer vácuo ligamos primeiro a bomba mecânica até alcançarmos a região de médio
vácuo, algo em torno de 10−4 Torr. Atingido essa pressão, ligamos a bomba turbomolecular de
alto vácuo alcançando a pressão de base. A pressão de base utilizada no crescimento dos nanofilmes de AlN foi de 9.7 x 10−6 Torr, e a pressão de trabalho foi 7.5 x 10−3 Torr. A temperatura
de operação no processo de crescimento foi 25° C.
Após a ejeção do gás argônio na câmara, o próximo passo é fazer o pré-sputerring que
também é uma forma de limpeza do alvo. Essa é uma das grandes vantagens desse método
de crescimento, pois permite remover impurezas da superfície do alvo e também conseguir
condições de equilíbrio entre o plasma e a temperatura. O tempo de pré-sputtering para todas
as nossas amostras foi de 5 minutos. Crescemos três séries de nanofilmes de AlN, os tempos
de deposição foram 10 horas, 5 horas e 3 horas. A leitura da fonte RF foi de 49 W de potência
direta (PD) e 1 W de potência refletida (PR).
C APÍTULO 3
33
Técnicas de Caracterização dos Filmes
“Já que o homem é o instrumento do seu próprio conhecimento, é necessário estudá-lo como um instrumento antes que possamos avaliar o valor do que os seus sentidos
nos dizem com respeito ao mundo.”
—BERTRAND RUSSELL (1872-1970)
3.1
Introdução
A difração de raios- X é uma técnica bastante usada para se obter características impor-
tantes sobre a estrutura de um composto qualquer. Os Raios-X podem ser produzidos fazendo
com que um feixe de elétrons de alta energia incida sobre um alvo metálico. Para obter a distância dos átomos no cristal e, consequentemente, a estrutura cristalina, um feixe de raios-X é
emitido sobre o cristal desconhecido. Devido sua natureza ondulatória, esse feixe é difratado
dando as medidas dos ângulos de difração dos raios emergentes. Por fim, os ângulos dos feixes resultantes da difração são lidos e processados por um computador que calcula e mostra as
configurações dos átomos no cristal.
A espectroscopia Ramam é uma técnica que permite a identificação de materiais, fornecendo
tanto suas características químicas quanto estruturais. Nesta técnica, não é necessário fazer
nenhuma preparação da amostra, como também, não há riscos de alterar as características do
material, pois sua análise é baseada na incidência de luz monocromática. De modo que, quando
a luz incidente é espalhada pelo material analisado, apenas uma pequena parte dessa luz, é
espalhada inelasticamente devido à interação da luz com a matéria. Essa é uma característica
intrínseca do material analisado e independe da frequência da luz incidente, e que permite a sua
identificação.
No presente capítulo, abordaremos de forma rápida e simplificada as técnicas de caracterização usadas em nossos nanofilmes, difração de raios-X e espectroscopia Ramam em suas
principais características.
3.2 DIFRAÇÃO DE RAIOS-X
3.2
3.2.1
34
Difração de Raios-X
Contextualização Histórica
Os raios-X foram descobertos no século XIX, em 1895, pelo físico alemão Wilhelm Conrad
Röntgen (1845 − 1923), primeiro prêmio Nobel de física em 1901, devido a seus experimentos
com raios catódicos (elétrons rápidos emitidos por metais). O experimento de Röntgen consistia
basicamente de um tubo de vidro, denominado tubo de raios catódicos, conectado a uma bomba
de vácuo, onde nos terminais opostos do tubo era aplicada uma voltagem de milhares de Volts
(∼ 1000 V), gerando uma corrente em seu interior.
Figura 3.1 Equipamentos utilizados por Röntgen. Em (a), o primeiro equipamento de raio-x produzido
no laboratório de Röntgen, e em (b) os equipamentos originais do seu laboratório [38].
Logo após a observação dos raios-X,1 Röntgen notou que um papel pintado com platinocianeto de bário, posto na mesma mesa de trabalho próximo ao tubo de raios catódicos, emitia
fluorescência, mesmo que o tubo de raios catódicos estivesse envolto por uma caixa de papelão.
Röntgen concluiu que os raios-X, apesar de apresentar propriedades semelhantes às da luz, não
podia ser luz comum, pois seus experimentos eram feitos sempre com o tubo de raios catódicos
completamente blindado por uma caixa de papelão. Na Figura 3.1, vemos os equipamentos
utilizados por Röntgen.
Röntgen passou a observar outras propriedades dessa estranha radiação, tais como, a propagação em linha reta - daí a formação de sombras bem definidas e delimitadas, a alta capacidade
de penetração em materiais, a insensibilidade a campos magnéticos e alta capacidade de impressionar chapas fotográficas. Por outro lado, sucessivas tentativas feitas por Röntgen para
verificar efeitos relacionados com reflexão, refração e difração resultaram infrutíferas, levando
1 Assim
denominados devido ao desconhecimento, por parte da comunidade científica da época, a
respeito da natureza dessa radiação.
3.2 DIFRAÇÃO DE RAIOS-X
35
o cientista a concluir que realmente se tratava de algo diferente de tudo o que se conhecia até
então por luz ou ondas eletromagnéticas. Mesmo assim, Röntgen publicou um artigo sobre seu
trabalho, onde juntava também radiografias obtidas, por exemplo, da mão de sua esposa.
Em 1912, o físico alemão Max von Laue (1879 − 1960) descobriu que o comprimento de
onda dos raios-X de Röntgen era da ordem de 10−10 metros (1 Agnstrom (Å)), daí ele suspeitou
que um cristal, cujo parâmetro de rede é desta ordem de magnitude, seria uma grade ideal para
um experimento de difração com raios-X [39].
Laue apresentou suas idéias para o professor e físico alemão Arnold Johannes Wilhelm Sommerfeld (1868 − 1951) e este levantou uma série de objeções, desencorajando-o em relaçãao ao
experimento. Laue então convenceu dois pesquisadores, seu técnico W.Friedrich e um estudante P. Knipping a fazerem o experimento, o qual se tornou um enorme sucesso. Na primavera
de 1912, eles obtiveram o primeiro diagrama de difração de raios-X em cristais, utilizando um
cristal cúbico de sulfato de cobre. Por este trabalho, Laue ganhou o prêmio Nobel de física de
1914 [40].
Figura 3.2 Padrão de difração de raios-X como obtido por Laue e colaboradores [41].
O trabalho de Laue sobre difração de raios-X, foi analisado detalhadamente pelo físico, químico e matemático britânico William Henry Bragg (1862 − 1942) e seu filho William Lawrence
Bragg (1890 − 1971) na estrutura denominada esfarelita, (zincblend) ZnS. Eles tentaram explicar o padrão de difração deste material com a idéia de que os pontos do padrão seriam produzidos da interação dos raios-X com a rede cristalina. Então, o físico escocês Charles Thomson
Rees Wilson sugeriu que W. L. Bragg refletisse raios-X por uma face de clivagem do cristal de
esfarelita. O sucesso da reflexão fez com que W.H. Bragg construísse um espectrômetro de
raios-X, o qual permite uma medida quantitativa das intensidades de raios-X. O experimento
com o ZnS foi um sucesso, espectros de difração de raios-X foram obtidos, confirmando a hipótese de Laue de que estes raios eram na verdade ondas eletromagnéticas, possuindo todas
as características dessas ondas, tais como reflexão, refração, difração, dentre outros. Tal desco-
3.2 DIFRAÇÃO DE RAIOS-X
36
berta teve grande impacto no mundo científico, tanto que, além de Laue, laureado com o prémio
Nobel de física de 1914, a dupla Bragg conquistaram o Nobel de 1915 [42].
3.2.2
Geração e emissão de Raios-X
Raios-X podem ser produzidos fazendo com que um feixe de elétrons de alta energia incida
sobre um alvo metálico. O espectro de raios-X produzido desta maneira, têm duas componentes,
uma contínua e outra discreta. A componente contínua, também conhecida por bremsstrahlung
ou radiação de freamento é proveniente da desaceleração dos elétrons ao interagirem com o
material do alvo (toda partícula carregada emite radiação eletromagnética ao ser acelerada). A
componente discreta, conhecida como radiação característica, é proveniente do decaimento dos
átomos que tiveram elétrons excitados ou ejetados ao interagirem com os elétrons do feixe de
alta energia.
A produção dos raios-X, pode ser explicada do seguinte modo: os elétrons que são emitidos
pelo catodo são fortemente atraídos pelo anodo e chegam a este com grande energia cinética,
devido a alta voltagem aplicada (da ordem de milhares de Volts). Chocando-se com o anodo, os
elétrons perdem a energia cinética e cedem energia aos elétrons que estão ligados aos átomos
no anodo. Assim, estes elétrons são então acelerados, emitindo ondas eletromagnéticas que são
os raios-X.
Os dois tipos distintos de emissão de raios-X dependem do tipo de interação entre os elétrons
acelerados e o alvo (anodo). A Figura 3.3, apresenta o espectro de raios-X emitido pelo alvo de
molibdênio, a 35 kV. O espectro mostra a radiação contínua de raios-X e dois picos de radiação
característicos que são designados por linhas Kβ e Kα [43].
Figura 3.3 Espectro de emissão de raios-X produzido quando se utiliza o metal Molibdênio como alvo
numa ampola de raios-X, funcionando a 35kV [43].
3.2 DIFRAÇÃO DE RAIOS-X
37
Assim, temos:
. A radiação de linha, que é a radiação característica do anodo e corresponde à emissão de
um fóton durante a transição de um elétron de uma camada de mais alta energia para outra de
mais baixa energia.
. Radiação de freamento ou bremsstrahlung, que é a radiação eletromagnética emitida pelos
elétrons rápidos durante seu brusco processo de desaceleração quando se chocam e são freados
pela matéria.
Quando um elétron sofre uma trasição atômica de uma camada de energia mais alta para
outra camada de menor energia, no interior de um átomo, uma linha característica de emissão
atômica é observada, conforme foi dito acima, essa emissão é chamada emissão de linha [33].
As camadas atômicas encontram-se relacionadas aos níveis discretos de energia dos elétrons
ligados ao átomo e correspondem ao número quântico principal, n=1,2,3,..., onde as primeiras
camadas são K,L,M,... Assim, por exemplo, as linhas de emissão associadas com transições
eletrônicas para o estado 1s (camada K), são chamadas linhas da série-K. Similarmente, linhas
associadas a transições eletrônicas para o estado 2s (camada L) são denominadas linhas da
série-L, e assim por diante. Se desejarmos produzir linhas de emissão de raios-X da série-K,
o átomo radiante deve ser, obviamente, ionizado inicialmente a partir de uma camada-K. Uma
linha de emissão da série-L exige que o átomo seja ionizado a partir de uma camada-L, e assim
sucessivamente.
Quando o metal alvo é bombardeado por elétrons rápidos, os elétrons ligados do metal,
pertencentes a uma dessas camadas, delas são arrancados, deixando em seus lugares vacâncias.
Estes níveis vacantes, podem então receber elétrons das camadas superiores com consequente
emissão de fótons com energias correspondentes a diferença entre os dois níveis, como ilustrado
na Figura 3.4.
Figura 3.4 Processo de geração de raios-X no interior de um átomo [42].
Quando um elétron da camada L, por exemplo, é transferido para a camada K, passando a
ocupar uma vacância do nível, ocorre um efeito de produção de fótons com energia da por:
3.2 DIFRAÇÃO DE RAIOS-X
φK − φL
38
(3.1)
tais fótons são denominados fótons de raios-X. A energia desta radiação é:
hc
,
(3.2)
λ
onde h é a constante de Planck, e c a velocidade da luz. A região do espectro eletromagE = hν =
nético de raios-X está no intervalo 0.1 − 100 Å, ou seja, entre a região dos raios-γ e a de raios
ultravioleta, ver Figura 3.5. Em energia, tal intervalo corresponde 0.1 − 100 keV.
Figura 3.5 Localização dos raios-X no espectro eletromagnético [44].
Na desaceleração, ou efeito de "Bremsstrahlung", o elétron em movimento tem sua trajetória desviada pela positividade do núcleo. Este desvio de trajetória é acompanhado por uma
desaceleração que faz com que parte da energia cinética do elétron seja emitida como fóton de
raios-X, que terá maior energia (maior freqüência) tanto quanto maior for o ângulo de desvio
da trajetória e quanto mais próximo estiver este elétron do núcleo, ver Figura 3.6.
A desaceleração tem pouca chance de ocorrer em regiões próximas ao núcleo, devido a
densidade nuclear. Na verdade, o átomo é bem diáfano, para se ter uma idéia, comparando o
tamanho do núcleo atômico a uma laranja, o limite do átomo de um determinado elemento estaria, por exemplo, a 3 km de distância. Assim, a maioria dos elétrons sofre interações distantes
do núcleo e produzem fótons de baixa energia, agora não mais numa faixa de energia característica, mas em uma variação constante, dependendo do cosseno do ângulo do desvio[34].
A probabilidade do fenômeno ocorrer também é pequena, porém tende a ser a maior fonte de
fótons de raios-X se comparado a outros fenômenos.
3.2 DIFRAÇÃO DE RAIOS-X
39
Figura 3.6 Ilustração do efeito Bremsstrahlung [42].
3.2.3
Equação de Bragg para Difração
A explicação completa para o fenômeno de difração de raios-X, quando o alvo é um cristal,
foi dada por W. L. Bragg em 1912, resultando na famosa lei denominada "Lei da difração de
Bragg", expressa na forma:
nλ = 2dhkl sin(θ),
(3.3)
onde λ é o comprimento de onda de raios-X, dhkl é a distância interplanar, ou seja, entre
dois planos cristalográficos consecutivos, indexados por (hkl), e θ é o ângulo entre o feixe de
raios-X incidentes e o plano cristalográfico de incidência, conforme ilustra a Figura 3.7.
Vamos agora examinar as condições necessárias para a difração de raios-X por um arranjo
periódico de átomos. Considere os dois planos de átomos paralelos A-A’ e F-F’ como na Figura
3.7, os quais possuem os mesmos índices de Miller h, k e l, que estão separados por uma
distancia d. Suponha que um feixe de raios-X paralelo, monocromático e coerente (em fase),
como comprimento de onda λ, esteja incidindo sobre os dois planos segundo um ângulo θ [45].
Dois raios nesse feixe, identificados como O e O’, são dispersos pelos átomos E e C. Se a
diferença entre o comprimento das trajetórias O-E-P’ e O’-C-P” (ou seja, BC + CD) for igual
a um numero inteiro, n, de comprimentos de onda, uma interferência construtivas dos raios
dispersos P’ e P” irá ocorrer segundo um ângulo θ em relação aos planos. Assim, a condição
para difração é:
nλ = BC +CD,
(3.4)
3.2 DIFRAÇÃO DE RAIOS-X
40
Figura 3.7 Esquema de difração dos raios-X [42].
ou, como pode ser visto pela geometria da figura:
nλ = dhkl sin(θ) + dhkl sin(θ) = 2dhkl sin(θ).
(3.5)
Dessa forma, temos uma expressão simples que relaciona o comprimento de onda dos raiosX e o espaçamento interatômico ao ângulo do feixe difratado. Se a lei de Bragg não for satisfeita, então a interferência será de natureza não-construtiva e será produzido um feixe de
difração de intensidade muito baixa [45].
3.2.4
Difração de Raios-X
Ao atingirem um material qualquer os raios-X podem ser espalhados elasticamente, sem
perda de energia pelos elétrons de um átomo do material, é o que chamamos de dispersão ou
espalhamento coerente. Após a colisão com o elétron, o fóton do raio-X muda sua trajetória,
porém mantendo a mesma fase e energia do fóton incidente. Do ponto de vista da física ondulatória, pode-se dizer que essa onda eletromagnética é instantaneamente absorvida pelo elétron
e reemitida. Assim, cada elétron atua como um centro de emissão de raios-X [43].
Se os átomos que geram este espalhamento estiverem arranjados em uma estrutura cristalina,
apresentando entre si distâncias próximas ao do comprimento de onda da radiação incidente,
pode se verificar que as relações entre esses espalhamentos tornam-se periódicas e que os efeitos
da difração dos raios-X podem ser observados em vários ângulos. Como dito na seção anterior,
as condições para que ocorra a difração de raios-X (interferência construtiva) dependerão das
condições expressas pela lei de Bragg, Equação 3.7.
A intensidade da radiação difratada depende, dentre outros fatores, do número de elétrons
3.2 DIFRAÇÃO DE RAIOS-X
41
no átomo e de como esses átomos estão distribuídos no espaço, de modo que os vários planos
de uma estrutura cristalina, possuem diferentes densidades de átomos e elétrons, fazendo com
que, as intensidades difratadas sejam distintas para os diversos planos cristalinos. Os planos
de difração e suas respectivas distâncias interplanares, bem como as densidades de átomos
(elétrons) ao longo de cada plano cristalino, são características específicas e únicas de cada
material cristalino, da mesma forma que o padrão difratométrico por ele gerado [46].
Se incidirmos um feixe de raios-X em ângulos variáveis em uma amostra com certa distribuição de pequenos cristalitos (amostra na forma de pó) e colocarmos essas intensidades
em função do ângulo de espalhamento 2θ (ângulo entre a onda incidente e a onda espalhada),
iremos obter um gráfico chamado difratograma, como mostrado na Figura 3.8. O padrão de
difração é único para cada tipo de cristal. Dessa forma, é possível descobrir a composição de
materiais através da difração de raios. Esse processo é chamado caracterização.
Figura 3.8 Padrão de difração (difratograma) de pó do NaCl [40].
A Figura 3.8, mostra um difratograma ou padrão de difração para uma amostra pulverizada
de sal de conzinha (NaCl). Os picos de alta intensidade resultam quando a condição de difração
de Bragg dada pela Equação 3.7, é satisfeita por algum conjunto de planos cristalográficos.
Nesta figura, esses picos estão identificados por seus índices de planos. Para calcular a distância
interplanar, quando α = β = γ = 90° (caso do NaCl), utilizamos a expressão:
dhkl = q
1
h2
a2
2
2
+ bk2 + cl 2
,
(3.6)
42
3.2 DIFRAÇÃO DE RAIOS-X
onde a, b e c são os parâmetros de rede do cristal considerado. Como exemplo, para o plano
220 (hkl=220) do cristal de NaCl (simetria cúbica, com parâmetros de rede a = b = c = 5.640
Å), temos :
dhkl = q
1
22
2
2
2
0
+ (5.640)
2 + (5.640)2
(5.640)2
= 1.994.
Substituindo o valor na lei de Bragg Equação 3.7, podemos encontrar o ângulo de Bragg
(ângulo onde há um pico de intensidade devido à interferência construtiva das ondas espalhadas)
relativo a esse plano:
1.54 = 2(1.994) sin(θ)
sin(θ) =
1.54
= 0.386
3.988
θ = 22.7
Note que usamos 1.54 Å para o valor de λ. Trata-se do comprimento de onda Kα1 do Cobre,
um dos materiais mais utilizados como alvo em tubos de raio-X [40].
O significado desses cálculos é que, incidindo um feixe de raios-X a um ângulo de incidência
de 22.7º, haverá um pico de intensidade, devido ao plano 220. Se incidirmos o feixe em ângulos
variáveis em uma amostra com uma certa distribuição de pequenos cristalitos (amostra na forma
de pó) e colocarmos essas intensidades em função do ângulo de espalhamento 2θ (ângulo entre
a onda incidente e a onda espalhada), iremos obter um gráfico chamado difratograma, como
visto na Figura 3.8.
O difratômetro é um aparelho usado para determinar os ângulos nos quais ocorre a difração em amostras pulverizadas. Cada partícula pulverizada é um cristal e a existência de um
grande número destas orientações aleatórias assegura que algumas partículas estão orientadas
de maneira correta, tal que todos os conjuntos de planos cristalográficos possíveis estarão disponíveis para a difração. A Figura 3.9, mostra esquematicamente as principais características
de um difratômetro. Uma amostra S no formato de uma chapa plana é posicionada de forma
que são possíveis rotações ao redor do eixo identificado por O, sendo esse eixo perpendicular
ao plano da página. No ponto T é gerado um feixe monocromático de raios-X e as intensidades
dos feixes difratados são detectadas através de um contador, identificado por C. A amostra, a
fonte de raios-X e o contador estão no mesmo plano [45].
O contador é montado sobre uma plataforma móvel que também pode girar ao redor do eixo
O e sua posição angular em termos de 2θ é marcada sobre uma escala graduada. A plataforma e
3.3 ESPECTROSCOPIA RAMAN
43
Figura 3.9 Ilustração esquemática de um difratômetro de raios-X, T(fonte), S(amostra), C(detector) e
O(eixo ao redor do qual giram a amostra e o detector) [45].
a amostra estão acopladas mecanicamente, de modo que uma rotação da amostra de um ângulo θ
é acompanhada de uma rotação de 2θ do contador, assegurando assim que os ângulos incidentes
e de reflexão sejam mantidos iguais um ao outro. À medida que o contador se move a uma
velocidade angular constante, um registrador escreve automaticamente a intensidade do feixe
difratado (monitorada pelo contador) em função do valor de 2θ; 2θ é chamado de ângulo de
difração e é medido experimentalmente. Colimadores são incorporados dentro da trajetória do
feixe para produzir um feixe bem focado e definido. A utilização de um filtro proporciona um
feixe praticamente monocromático.
3.3
Espectroscopia Raman
3.3.1
Contextualização Histórica
O espalhamento inelástico de uma luz monocromática foi predito teoricamente pelo físico
austríaco Gustav Adolph Stephan Smekal (1895-1959) em 1923 e foi demonstrado e explicado
corretamente pelo Sir Chandrasekhara Venkata Raman (1888-1970), cientista indiano nascido
na cidade de Trichi, no Sul da Índia. Em 1902, com apenas 14 anos, Raman graduou-se em
primeiro lugar no curso de física. Concluiu seu mestrado em 1907 e quinze anos depois, publicou o trabalho "Difração molecular da luz", o primeiro de uma série que o levou, em 1928,
a descobrir um interessante efeito de difusão da luz ao atravessar materiais transparentes que
tomou seu nome, "Efeito Raman", lhe valendo o prêmio Nobel de física em 1930 [47].
3.3 ESPECTROSCOPIA RAMAN
44
Figura 3.10 Aparato utilizado por Raman [48].
3.3.2
Espectroscopia Ótica
Todos os picos de um espectro são devido às transições entre estados de energia. A espectroscopia molecular fornece o valor da variação da energia interna quando uma molécula
absorve, emite ou espalha a radiação eletromagnética em quantidades discretas ou quantizadas.
Espectroscopia é o ramo da ciência que trata da obtenção e da análise qualitativa e quantitativa
dos espectros de emissão, absorção e espalhamento das amostras. Muito do nosso conhecimento
atual acerca da estrutura da matéria é baseado em investigações espectroscópicas. Quando a radiação interage com a matéria, espectros de emissão, absorção e espalhamento são gerados.
Assim, informações sobre a estrutura molecular e sobre as interações das moléculas com sua
vizinhança, podem ser obtidas [49].
A espectroscopia ótica não altera as características do material analisado, como acontece
com algumas técnicas que utilizam a incidência de elétrons ou íons nas amostras. Em meados
da década de 60, com a introdução do uso de lasers na excitação do espectro Raman, a espectroscopia Raman tornou-se um método amplamente utilizado em matérias líquidos, sólidos e
gasosos.
A natureza do efeito Raman pode ser explicada tanto pela teoria clássica como pela quântica.
Entretanto, a teoria clássica tem algumas limitações, não podendo ser aplicada para rotações
moleculares, pois a teoria clássica não descreve frequências, rotações discreta, dentre alguns
outros inconvenientes. Embora o modelo clássico forneça um bom resultado para as frequências
do espectro Raman, para se obter uma relação para a intensidade do espectro devemos descrever
o espalhamento Raman por um modelo quântico [50].
O quantum de energia, ∆E, é função do comprimento de onda da radiação, λ, de acordo
com a equação:
∆E =
hc
,
λ
(3.7)
3.3 ESPECTROSCOPIA RAMAN
45
onde h é a constante de Planck e c é velocidade da radiação eletromagnética. No meio em
que o comprimento de onda foi medido. A velocidade, c, e o comprimento de onda, λ, estão
relacionados à freqüência da radiação, ν, pela fórmula:
λν = c.
(3.8)
Os valores de c e λ dependem do meio em que a medição é feita, contudo a frequência
correspondente não, sendo dada pela relação:
c
c
( )ar = ( )vacuo = ν.
(3.9)
λ
λ
Em geral, é mais informativo empregar a freqüência ν, em Hz do que o comprimento de
onda, λ em metros, porque a variação entre dois níveis de energia molecular ∆E/h é numericamente igual à freqüência da radiação, expressa pela fórmula abaixo:
∆E
= ν(Hz)
h
ou ∆E = E (1) − E (2) = hν( joule).
(3.10)
Se uma molécula em um estado de menor energia E (2) pode ser excitada para outro de
maior energia E(1) pela absorção de uma radiação eletromagnética de freqüência ∆E/h, sendo as
energias E(1) e E(2) valores precisos, a radiação absorvida será essencialmente monocromática e
todas as demais freqüências terão intensidades desprezíveis. A situação descrita anteriormente
corresponde a um processo de absorção de radiação, contudo ela é válida para casos em que se
observa emissão ou espalhamento de radiação como no caso da espectroscopia Raman.
3.3.3
As Regiões do Espectro Eletromagnético
O espectro eletromagnético é um contínuo de energia, que para efeito de simplificação é
dividido em várias regiões as quais são associadas aos diferentes tipos de energia. A Tabela 3.1 e
a Figura 3.11 resumem estas informações, é preciso ter em mente que as fronteiras apresentadas
não são precisas.
Em energias acima de 3 x 1020 Hz, região de raios γ, a troca de energia envolve o rearranjamento de partículas nucleares. No intervalo de energia de 3 x1018 a 3 x 1016 Hz, região de
raios-X, as trocas de energia envolvem elétrons internos da molécula. No intervalo de energia de
3 x 1014 a 3 x 1016 Hz, regiões visível e ultravioleta, as trocas de energia envolvem transferência
de elétrons de valência de um orbital para outro.
46
3.3 ESPECTROSCOPIA RAMAN
Região
C. de Onda(Å)
C. de Onda(cm)
Frequência (Hz)
Energia (eV)
> 10−5
> 109
> 10
Micro-ondas
109 à 106
10 à 0.01
3 x 109 à 3 x 1012
> 10−5 à 0.01
Infra-vermelho
106 à 7000
0.01 à 7 x 10−5
3 x 1012 à 4 x 1014
0.01 à 2
Rádio
Visível
Ultravioleta
Raios-X
Raios Gama
7000 à 4000
4000 à 10
7x
10−5
4x
>3x
à4x
10−6
à
106
10−7
4x
1014
7x
1014
109
à7x
1014
2à3
à3x
1017
3 à 103
10 à 0.1
10−7 à 10−8
3 x 1017 à 3 x 1019
103 à 105
< 0.1
< 0.1
> 3 x 19
> 105
Tabela 3.1 Valores aproximados de comprimentos de onda, frequência e energia para algumas regiões
do espectro eletromagnético [51].
Devido ao fato das energias notadas em Hertz conduzirem a números muito grandes, é
comum expressar a frequência em número de onda (cm−1 ) ou como comprimento de onda em
nanômetro (nm). No intervalo de energia de 3 x 1012 a 3 x1014 Hz ou de 100 a 10000 cm−1 ou
de 100 a 1 microns, fica a região do infravermelho. Estas energias estão associadas às vibrações
moleculares. O estudo do assunto é denominado espectroscopia vibracional [44].
No intervalo de energia de 3 x 1011 a 109 Hz ou 30 a 10 cm−1 , região de microondas, as
trocas de energia envolvem transições entre níveis rotacionais das moléculas.
No intervalo de energia de 3 x 106 a 109 Hz (10m a 30cm), situa-se a região de rádio frequência, onde as trocas de energia correspondem às inversões de spin de um núcleo ou elétron. Estas
técnicas são chamadas de espectroscopia de ressonância magnética nuclear e de espectroscopia
de ressonância de spin eletrônico.
A espectroscopia Raman estuda o efeito do espalhamento da radiação, com o qual se obtém
informação a respeito das energias dos níveis vibracionais e rotacionais das moléculas. A informação obtida é muitas vezes complementar àquelas obtidas nas regiões do infravermelho e
de microondas, mas o espalhamento Raman da luz ocorre nas regiões visível e ultravioleta do
espectro eletromagnético [51].
3.3 ESPECTROSCOPIA RAMAN
47
Figura 3.11 Espectro eletromagnético [52].
3.3.4
O Efeito Ramam
A espectroscopia Raman é a principal técnica usada atualmente na obtenção de informações
sobre as estruturas químicas e as formas físicas, identificando e determinando quantitativamente
ou semi-quantitativamente as quantidades de uma substância em uma amostra, através dos seus
padrões espectrais característicos. As amostras analisadas podem ser examinadas em toda uma
gama de estados físicos, por exemplo, como sólidos, líquidos ou vapores, no estado frio ou
quente, a granel, como partículas microscópicas, ou como camadas superficiais.
O efeito Raman fornece muitas informações sobre os estados quânticos moleculares, trata-se
do espalhamento da luz por moléculas com uma mudança de freqüência. Existem outros processos de espalhamento da luz, no espalhamento Rayleihg (John William Strutt,1842 − 1919,
também conhecido como o 3º Barão de Rayleigh) a frequência da luz espalhada é igual ao da
luz incidente. Já no processo de fluorescência, a frequência da luz incidente coincide com a
frequência de absorção das moléculas espalhadoras do gás. Este é um fenômeno de ressonância
onde a molécula é levada a um estado excitado e, após um breve tempo de vida, reemite luz
numa frequência diferente. No efeito Raman, a frequência da luz espalhada também é diferente
da frequência da luz incidente, mas esta frequência incidente da luz não está relacionada com
alguma frequência característica das moléculas espalhadoras [53]. A diferença entre as frequências das radiações incidente e espalhada está relacionada à criação ou aniquilação de fônons no
material.
3.3 ESPECTROSCOPIA RAMAN
48
Quando uma radiação monocromática de frequência ν0 incide em uma célula contendo uma
substância transparente, sem material em suspensão, a maior parte da radiação a atravessa sem
alterações. Entretanto, uma pequena fração da radiação (≈ 0, 1%) é espalhada pelas moléculas
da amostra em todas as direções.
A intensidade total da radiação espalhada é da ordem de 10−3 a 10−5 vezes o da intensidade
total da radiação incidente e a maior parte desta radiação espalhada tem a mesma freqüência
ν0 da radiação incidente, denominado espalhamento Rayleigh. O espalhamento Raman corresponde à fração de cerca de 10−7 da intensidade incidente. Assim, o efeito Raman é muito fraco,
o que exige o uso de monocromadores com excelentes características em manter a luz dissipada
em níveis muito baixos. Caso contrário, o efeito Raman será mascarado. Também é necessário
o uso de detectores sensíveis e sistemas óticos eficientes [54].
A radiação espalhada contém fótons com a mesma frequência ν0 da radiação incidente em
virtude do espalhamento elástico, mas também contém fótons de outras frequências devido ao
espalhamento inelástico tais como (ν0 + ν1 ) e (ν0 − ν1 ). As linhas de menores freqüências
do que a incidente (ν0 − ν1 ), são conhecidas como linhas de Stokes e as linhas de maiores
frequência (ν0 + ν1 ), são denominadas de linhas anti-Stokes, ver Figura 3.14 .
Figura 3.12 Diagramas de níveis de eneregia para os efeitos Stokes e anti-Sotkes.
No processo Stokes (ν0 − ν1 ), o fóton espalhado tem energia menor do que o fóton incidente
uma vez que parte da energia deste foi fornecida ao material na criação de um fônon. No
processo anti-Stokes (ν0 + ν1 ), o fóton espalhado tem energia maior do que o fóton incidente e
a diferença está relacionada à energia do fônon que foi aniquilado da rede [55].
3.3 ESPECTROSCOPIA RAMAN
49
Figura 3.13 Os efeitos Stokes e anti-Sotkes em um espectro Raman.
A conservação da energia no processo de espalhamento Raman é dada pela relação:
h̄νi = h̄νe ± h̄ν f ,
(3.11)
onde νi , νe e ν f são, respectivamente, a frequência do fóton incidente, a frequência do fóton
espalhado e a frequência do fônon.
O que faz as moléculas vibrarem, mesmo antes de receberem luz, é a agitação térmica. O
ambiente, onde está a amostra, troca calor (energia) com as moléculas, excitando algumas delas em seus modos normais de vibração. Essas produzem o espalhamento Raman anti-Stokes.
Normalmente, em uma amostra a temperatura ambiente, o número de moléculas que estão no
estado fundamental é muito maior que o número de moléculas já excitadas termicamente. Portanto, o número de processos do tipo Stokes é maior que o número de processos anti-Stokes. A
magnitude da variação de frequência (variação Stokes) depende das freqüências dos modos do
fônon óptico suportadas pelo material.
É importante destacar que nem todo modo de vibração de uma molécula pode produzir
espalhamento Raman. Os que podem são chamados de modos ativos para esse tipo de espalhamento. Alguns modos não podem ser excitados por esse tipo de espalhamento e são ditos
inativos. Entretanto, não basta que a frequência da radiação coincida com a frequência de vibração normal do material para que o fóton seja absorvido. Para haver absorção, além dessa
coincidência de frequências (ou energias), é necessário que a radição gere um momento de dipolo elétrico na molécula ou, se a molécula já tem um momento de dipolo, a vibração precisa
fazer esse momento de dipolo variar.
Assim, para um modo ser Raman ativo existe a necessidade da variação da polarizabilidade
da molécula durante a vibração, isto é, o momento do dipolo a ser considerado é induzido pela
radiação eletromagnética. O campo elétrico produzido pelo feixe de radiação monocromática
3.3 ESPECTROSCOPIA RAMAN
50
polariza os elétrons da molécula em ressonância, promovendo a deformação da nuvem eletrônica molecular. Nesta distorção, a carga positiva do núcleo é atraída em direção oposta ao pólo
negativo do campo elétrico, com o elétron sendo atraído em direção oposta ao pólo positivo.
Esta separação de cargas causa uma indução no momentum de dipolo, e diz-se que a molécula
está polarizada [56].
Assim, para haver absorção da radição incidente, a vibração deve variar o momento de
dipolo da molécula. Note que a frequência de vibração do dipolo coincide com a frequência
da luz incidente. Na Figura 3.14, é mostrado a descrição clássica do espalhamento Raman.
Uma molécula sofre uma polarização induzida pelo campo elétrico oscilante devido a radiação
incidente. Este dipolo induzido, em seguida, irradia luz difusa, com ou sem troca de energia
com os possíveis modos vibracionais da molécula.
Figura 3.14 Polarização induzida em uma molécula por campo elétrico. A radiação espalhada pode
estar em vários sentidos, na figura são mostrados em 90° e 180º [57].
Quanto maior o campo, maior o momento de dipolo, segundo a expressão:
P = αE.
(3.12)
Esse α é chamado de polarizabilidade e mede a disposição da molécula a ter momento de
dipolo e para haver efeito Raman a polarizabilidade deve variar.
3.3.5
A Espectroscopia Raman
Até aproximadamente 1986, os estudos sobre o efeito Raman tinham somente caráter acadêmico, com relativamente poucos relatórios de espectroscopia Raman realmente aplicada à
análise química. Os impedimentos para aplicações gerais de espectroscopia Raman para as
análises químicas eram essencialmente tecnológicos e não fundamentais. A instrumentação necessária para observar o efeito Raman (em razão da sua fraca intensidade) era demasiadamente
3.3 ESPECTROSCOPIA RAMAN
51
custosa para que se realizassem procedimentos de análise química usuais. Devido às inovação
tecnológica e científica, nos últimos anos, ampliou-se significativamente a aplicabilidade da
espectroscopia Raman, especialmente em análise química [57].
Dentre alguns fatores que contribuíram para essa revolução, podemos citar os dispositivos
CCD (charge-coupled device)2
Figura 3.15 CCD (charge-coupled device) ou Dispositivo de Carga Acoplada, especialmente desenvolvido para uso na obtenção de imagens no ultravioleta [58].
Para analisar uma determinada amostra por espectroscopia Raman, deve ser feito uma série
de opções, no intuito de decidir qual a melhor forma de caracterizar essa amostra. Assim, as escolhas feitas são em última instância, determinadas pela disponibilidade de equipamentos e pelo
tipo de resposta requerido. Existe uma gama de variáveis na caracterização por espectroscopia
Raman, que vão desde a escolha da fonte de excitação, dispositivos, detectores e acessórios
adequados que permitirão que a amostra seja estudada de uma forma eficiente.
A espectroscopia Raman pode ser classificada baseada na fonte de emissão de radiação
utilizada, como por exemplo: ultravioleta (UV), visível, infra-vermelho (IR) entre outras. Os
lasers mais comuns utilizados na espectroscopia Raman no infra-vermelho são, neodímio ítrioalumínio-granada (Nd:YAG), e titânio-safira (Ti: safira) [50].
A espectroscopia Raman também é classificada de acordo com a tecnologia empregada,
por exemplo, Transformada de Fourier (FT-Raman) ou de sistemas dispersivos. O sistema FTRaman tem inúmeras vantagens sobre o sistema dispersivo, incluindo a vantagem multiplex
2 CCD
(charge-coupled device) ou Dispositivo de Carga Acoplada é um sensor para captação de imagens for-
mado por um circuito integrado contendo uma matriz de capacitores ligados, sob o controle de um circuito externo. Cada capacitor pode transferir sua carga elétrica para um outro capacitor vizinho. Os CCDs são usados em
fotografia digital, imagens de satélites, equipamentos médico-hospitalares, na astronomia ( fotometria), óptica e
espectroscopia UV . A capacidade de resolução ou detalhe da imagem depende do número de células fotoelétricas
do CCD. Expressa-se este número em pixels. Quanto maior o número de pixels, maior a resolução da imagem.
Atualmente, as câmeras fotográficas digitais incorporam CCDs com capacidades de até 160 milhões de pixels[45],
melhores detectores, espectrógrafos compactos, filtros mais eficientes, laser infravermelho, melhorias computacionais, entre vários outros fatores, contribuíram sobre maneira, para essa grande revolução na instrumentação Raman
e suas aplicações analíticas [58].
3.3 ESPECTROSCOPIA RAMAN
52
o qual lidera a capacidade de coletar vários comprimentos de onda em um curto período de
tempo. Entretanto, a espectroscopia Raman dispersiva tem se tornado muito mais popular desde
o advento do CCD (charge-couple device detector) devido ao seu grau de eficiência quântica
[59].
Na Figura 3.16, mostramos um diagrama típico de um equipamento necessário para a obtenção de um espectro Raman. O sistema é constituído de uma fonte de radiação monocromática
(de energia maior que a energia de vibração molecular da amostra, porém, menor que a energia
de excitação eletrônica), um dispositivo para suporte da amostra, um espectógrafo para dispersão da radiação espalhada, polarizadores, espelhos, grades, um dispositivo de detecção da luz
que pode ser de natureza fotográfica, de natureza fotoelétrica ou de natureza de cargas acopladas
(CCD), e um computador [60].
Figura 3.16 Diagrama típico de um equipamento necessário para a obtenção de um espectro Raman
[60].
O espectrômetro Raman, ilustrado na Figura 3.16, consiste em um triplo monocromador, um
microscópio óptico (usado para focalizar o feixe do laser na amostra e para coletar a luz retroespalhada) e um detector CCD. A luz proveniente do laser incide na amostra, focalizada pelo
microscópio óptico, que permite analisar uma região da amostra na ordem de até 1µm2 . A luz
retro-espalhada pela amostra é coletada pela objetiva do microscópio e levada ao espectrômetro.
No espectrômetro, a luz passa primeiramente por um duplo monocromador que é formado por
dois estágios, cada um consistindo de dois espelhos esféricos e uma rede de difração (M1, M2,
G1, M5, M6 e G2). O duplo monocromador é mais usado numa configuração que elimina
a luz espalhada que possui a mesma frequência do laser (espalhamento elástico). No segundo
estágio, a luz espalhada converge de maneira que seu foco esteja sobre a pequena fenda na saída
do duplo-monocromador (fenda S3). Ao sair do duplo monocromador, a luz é enviada a um
3.3 ESPECTROSCOPIA RAMAN
53
espectrógrafo (conjunto de espelhos esféricos M9 e M10 e grade G3), onde a luz sofre uma nova
dispersão e é enviada para o detector CCD. O sinal é então amplificado, digitalizado e enviado
ao computador. O sistema pode ser usado também no modo simples, onde a luz coletada pela
objetiva do microscópio é enviada diretamente para o espectrógrafo, sem passar pelo duplomonocromador. Porém, neste caso, são necessários filtros para impedir a passagem da luz
proveniente do espalhamento elástico, o que torna inviável usar este sistema em experimentos
onde são usados vários comprimentos de onda de excitação [61].
Um espectro Raman mede a relação entre comprimento de onda da radiação espalhada em
comparação ao da radiação de excitação (laser), ver Figura 3.17. E é "plotado"em cm−1 (inverso
de centímetro), sendo essa a unidade de energia preferida dos espectroscopistas. O espectro,
mostrado na Figura 3.17, foi obtido de uma ampola de vidro contendo pequena quantidade de
iodo e selada após ser feito vácuo, ficando a pressão na ampola igual à pressão de vapor do iodo
na temperatura ambiente. O espectro da Figura 3.17, excitado com 514, 5 nm, foi registrado no
espectrômetro Jobin-Yvon U-1000 [62].
Figura 3.17 Espectro Raman ressonante do vapor de iodo, excitação 514 nm, mostrando a banda fundamental (215 cm−1 ) e algumas das harmônicas [62].
O espectro Raman de uma determinada molécula consiste em uma série de picos ou faixas
devido à interação da radiação incidente (laser) com os modos vibracionais característicos das
moléculas (amostra). Os picos correspondem aos deslocamentos Raman em relação à energia da
radiação incidente hν0 . Os números acima dos picos são os respectivos valores das frequências
medidos em cm−1 .
3.3.6
Vibrações em Sólidos Cristalinos
O comportamento coletivo das vibrações que ocorrem em um sólido cristalino pode ser
considerado como uma superposição de ondas planas que se propagam para o infinito [63],
essas ondas ou modos normais de vibração, são comumente modelados pelos fônons. Qualquer
3.4 MICROSCOPIA DE FORÇA ATÔMICA (AFM)
54
onda é formada por pacotes de energia h̄ω, chamados quanta de energia. Assim, a energia de
uma onda é discreta e tem valor igual a um mutiplo de h̄ω, um quantum de uma onda tem
comportamento tanto de onda como de partícula, tendo energia e momentum dados por:
E = h̄ω
e
p = h̄k
(3.13)
As excitações em um sólido têm caráter de onda, sendo portanto quantizadas. Um quantum
de vibração da rede é um pacote de onda elástica, e recebe o nome de fônon [64]. Um fóton
incidindo em um cristal pode criar ou destruir um fônon, que é o quantum de energia que separa
os níveis de energia vibracional da rede cristalina. Como vibração de rede entende-se tantos
os modos internos, característicos de um agrupamento molecular, como os modos externos,
movimentos tipo translação ou rotação de íons ou agrupamentos moleculares.
Para um sólido tridimensional contendo N células unitárias com p átomos cada, (3pN − 6)
diferentes fônons podem se propagar e seus vetores de onda Kn pertencem a um volume no
espaço recíproco conhecido como Zona de Brillouin (ZB). Os modos normais de vibração dos
planos cristalinos que oscilam em fase com os planos vizinhos são os modos acústicos. Da
mesma forma, os modos normais de vibração que oscilam fora de fase em relação aos planos
em relação aos planos vizinhos são os modos ópticos. Alem disso, fônons ainda podem ser
classificados como longitudinais ou transversais dependendo de como os átomos movem-se
paralelos ou perpendiculares em relação á direção de propagação dada pelo vetor Kn .
3.4
Microscopia de Força atômica (AFM)
A microscopia de força atômica (AFM - Atomic Force Microscopy) é uma técnica recente
no estudo microscópico de superfícies. Em 1986, Binnig, Quate e Gerber [65] desenvolveram
um aparato experimental para medir forças em escala atômica. O princípio básico desta técnica
consiste em medir a deflexão de uma haste (de 100 a 200 µm de comprimento) que possui uma
extremidade onde está montada uma sonda.
A sonda consiste de uma ponta de silício, ver Figura 3.19, que ao passar por uma superfície
rugosa, mede as forças de interação entre a ponta da sonda e os átomos da superfície da amostra,
gerado deflexões na haste. Estas oscilações são então medidas e representarão a rugosidade da
superfície. A técnica é uma poderosa ferramenta topográfica gerando imagens em 3 dimensões
das superfícies com resolução atômica [66] [67].
3.4 MICROSCOPIA DE FORÇA ATÔMICA (AFM)
55
Figura 3.18 Representação esquemática do conjunto haste-sonda-amostra. No detalhe, a sonda e suas
dimensões nanométricas. [68].
Quando a sonda se aproxima da amostra, ela é afetada por uma força de atração originada
pela interação de Van der Waals. Esta atração aumenta até os átomos das duas superfícies começarem a repelir seus orbitais eletrônicos. A repulsão eletrostática enfraquece a força atrativa
à medida que a distância diminui. A força anula-se quando a distância entre os átomos é da ordem de alguns angstroms (distância características das ligações atômicas). Quando as forças se
tornam positivas, podemos dizer que os átomos da sonda e da amostra estão em contato. Neste
regime de interação as forças repulsivas são dominantes [68].
Para entender o funcionamento de um AFM deve-se ter o conhecimento das forças que agem
entre os sistemas nanoscópicos a distâncias muito pequenas. Na Figura 3.3, estão representadas
as forças que agem entre a sonda e a amostra em função da distância que as separa. Este tipo
de força é proveniente do potencial de Lennard-Jones entre dois ou mais átomos, ou qualquer
outro potencial de interação com uma dependência deste tipo na variável r.
Figura 3.19 O potencial de Lennard-Jones. Na área abaixo da linha de força nula, as forças são atrativas.
Acima desta linha, as forças são repulsivas [68].
C APÍTULO 4
56
Resultados
Uma vez que não podemos ser universais e saber tudo
quanto se pode saber acerca de tudo, é preciso saber-se
um pouco de tudo, pois é muito melhor saber-se alguma
coisa de tudo do que saber-se tudo apenas de uma coisa.
—BLAISE PASCAL (1623-1662)
4.1
Introdução
Neste capítulo será apresentado os resultados da caracterização dos nanofilmes usando três
técnicas, a difração de raios-X, microscopia de força atômica (AFM) e a espectroscopia Raman.
A análise por raios-X para altos e baixos ângulos foi realizada em dois equipamentos distintos.
No difratômetro de raios-X Shimadzu XD-7A pertencente ao Laborátorio de Magnetismo e Materiais Magnéticos, na (UFSM-LMMM).
Em seguida no difratômetro de raios-X MineFlex II, do fabricante Rigaku Corporation, do
grupo de Nanoestruturas Magnéticas da (UFRN-DFTE). A análise por espectroscopia Ramam
foi realizada na Universidade Federal do Ceará (UFC), por fim a microscopia de força atômica
(AFM) foi executada na Universidade Federal de Pernambuco (UFPE-CCEN)-Departamento
de Física.
4.2
Difração por Raios-X
4.2.1
Difratogramas da Alvo
Na caracterização por difração de raios-X, foi analisado inicialmente o alvo de nitreto de
alumínio usado em nossas deposições via sputtering. A Figura 4.1 mostra os resultados encontrados. A análise da figura mostra que o alvo usado em nossas deposições é realmente
constituído de nitreto de alumínio, os gráficos (a) e (b) dessa figura indicam os dois lados do
nosso alvo, que tem formato cilíndrico com diâmetro 5.1 cm e altura 0.6 cm, com 99, 8% de
57
4.2 DIFRAÇÃO POR RAIOS-X
pureza, fabricado pela Williams Advanced Research. Analisando os difratogramas vemos que
os picos característicos do AlN obtidos em nossas medidas estão totalmente de acordo com os
dados encontrados na literatura sobre esse material. Os índices nos picos correspondem aos
"índices de Miller"dos planos onde ocorre a difração, e foram por nós indexados com base na
ficha de dados sobre o nitreto de alumínio Natl. Bur. Stand. (U.S.) Monogr. 25, volume 12,
página 5 (1975). CAS Número: 24304-00-5.1
(a)
(b)
Figura 4.1 Difratograma do alvo de nitreto de aluminio usado em nossas deposições, onde os gráficos
(a) e (b) indicam os dois lados do nosso alvo.
Para efeito de comparação os gráficos da Figura 4.2 mostram o difratograma de um dos lados
do nosso alvo e o difratograma do pó de nitreto de alumínio comercial facilmente encontrado
na literatura sobre esse material. Nos gráficos da Figura 4.2 o eixo das abscissas que nesse caso
representa a variação do ângulo 2θ cresce da direita para esquerda. Na Figura 4.2, o gráfico (a)
é o difratograma do pó de nitreto de alumínio comercial [69], o gráfico (b) é de um dos lados do
alvo. A análise desses gráficos revela, como esperado, que os picos obtidos em nossas amostras
são característicos desse material (nitreto de alumínio) e encontram-se na mesma posição dos
obtidos no pó de nitreto de alumínio comercial, garantindo assim a confiabilidade do alvo usado
em nossas deposições.
1 encontra-se
no apêndice A dessa dissertação.
4.2 DIFRAÇÃO POR RAIOS-X
58
Figura 4.2 Difratogramas, em (a) pó de nitreto de alumínio comercial [69], em (b) um dos lados do
alvo.
59
4.2 DIFRAÇÃO POR RAIOS-X
4.2.2
Parâmetros de deposição
Os nanofilmes de nitreto de alumínio nesse trabalho foram crescidos usando o método magnetron sputtering RF não reativo, e foram depositados em três grupos distintos, variando-se seus
tempos de deposição entre 10, 5 e 3 horas. A limpeza dos substratos foi realizada da seguinte
forma: no ultrasom durante 10 minutos usando-se acetona, seguida de mais uma limpeza no
ultrasom de 10 minutos usando-se álcool metílico (metanol). Para limpar o alvo foi realizado
pré-sputtering durante 5 minutos antes do inicio das deposições. Assim crescemos primeiro os
nanofilmes com duração de 10 horas, em três substratos de vidro, após crescemos em três substratos, dois de vidro e um de silício três amostras com um tempo de 5 horas, também em vidro
e silício como substratos, crescemos mais três amostras com 3 horas, duas em vidro e uma em
silício. A Tabela 4.1 abaixo sintetiza os principais parâmetros envolvidos na deposição desses
nanofilmes.
Parâmetros
Substrato
Nanofilmes 10 horas Nanofilmes 5 horas Nanofilmes 3 horas
Vidro
Vidro e Silício
Vidro e Silício
Pressão de base
1.2 x 10−5 mbar
1.2 x 10−5 mbar
1.2 x 10−5 mbar
Pressão de trabalho
1.0 x 10−2 mbar
1.0 x 10−2 mbar
1.0 x 10−2 mbar
Potência direta
49 watts
49 watts
49 watts
Potencia refletida
1 watts
1 watts
1 watts
25°C
25°C
25°C
Temperatura
Tabela 4.1 Parâmetros envolvidos na deposição dos nanofilmes.
4.2 DIFRAÇÃO POR RAIOS-X
4.2.3
60
Difratogramas dos Nanofilmes
A seguir na Figura 4.3, são apresentados os difratogramas obtidos no raios-X MineFlex II,
grupo de Nanoestruturas Magnéticas da (UFRN-DFTE).
(a) AlN sobre vidro durante 10 horas
(b) AlN sobre vidro durante 10, 5 e 3 horas
(c) AlN sobre silício durante 3 horas
(d) AlN sobre silício durante 5 horas
Figura 4.3 Difratogramas das amostras depositadas em vidro e silício.
Da análise da Figura 4.3, gráficos (a) e (b) para as amostras depositadas em vidro com tempos 3, 5 e 10 horas nenhum pico característico do nitreto de alumínio é observado, nos gráficos
(c) e (d) da mesma figura, para as amostras depositadas sobre o substrato de silício com os
tempos de 3 e 5 horas, temos um total de três picos mas que, depois de analisados verificou-se
sendo característicos do silício, ou seja, do substrato. Assim de forma geral nos difratogramas
de nossas amostras não há picos característico do nitreto de alumínio. Os difratogramas feitos no Laborátorio de Magnetismo e Materias Magnéticos (UFSM-LMMM), concordam com
os difratogramas por nós obtidos, neles também não há picos que caracterizem o nitreto de
alumínio. Concluímos que os nanofilmes são amorfos, não apresentando cristalinidade.
61
4.2 DIFRAÇÃO POR RAIOS-X
4.2.4
Difratogramas dos Nanofilmes a Baixos Ângulos
Com a técnica de difração de raios-X a baixos ângulos, é feita a calibração da taxa de deposição (espessura de nanofilmes até 1000 Å), obtendo-se espessuras da amostras e consequentemente as taxas de deposições durante o processo de crescimento dos filmes nanométricos. As
Figuras 4.4 e 4.5, mostram os gráficos das medidas dos difratogramas a baixos ângulos obtidos
na (UFRN-DFTE).
(b) Ajuste linear para o vetor q.
(a) Picos a baixo ângulo, amostra AlN no vidro a 5 horas.
Figura 4.4 Difração de raio-X baixo ângulo para calibração da taxa de deposição. Gráfico (a) picos a
baixo ângulo obtidos para a amostra AlN no vidro a 5 horas, gráfico (b) vetor de espalhamento q versus
o índice dos picos de Bragg, ajustado linearmente.
Para determinarmos a espessura do filme, primeiro indexamos os picos de Bragg, relativos
as interferências construtivas das ondas refletidas nas interfaces ar/nanofilme e nanofilme/vidro
aos seus respectivos ângulos, como mostra a Figura 4.4 gráfico (a).
Com a localização dos picos de Bragg, pode-se construir um gráfico do vetor de espalhamento q versus o índice dos picos de Bragg. Ver Figura 4.4 gráfico (b). Temos que:
q=
4π sin(θ)
,
λ
(4.1)
onde λ = 1, 54056 Å é o comprimento de onda do raio-X. A inclinação da reta resultante
"P.A.", ajustada linearmente, está relacionado com a espessura do filme "d", da seguinte forma:
2π
(4.2)
P.A.
Usando o procedimento acima descrito, obtemos as espessuras dos nanofilmes com suas
d=
respectivas taxas de deposição.
4.2 DIFRAÇÃO POR RAIOS-X
(a) Amostra AlN sobre silício a 3 horas.
62
(b) Amostra AlN sobre vidro a 5 horas.
Figura 4.5 Difratogramas a baixos ângulos e ajustes lineares. Onde temos em (a) AlN sobre silício
depositado durante 3 horas e em (b) AlN sobre vidro depositado durante 5 horas.
Vemos que a curva do gráfico (a) correspondente a amostra de nitreto de alumínio depositado
sobre silício com tempo de 3 horas, não exibe picos tão definidos e proeminentes quanto os picos
da curva do gráfico (b), que foram obtidos da amostra de nitreto de alumínio depositado sobre
o vidro com tempo de 5 horas. No gráfico (a), a espessura do nanofilme calculado usando as
equações 4.1 e 4.2, e ajustado pelo método descrito, é de d = 12.833 nanômetros.
O primeiro pico desse gráfico, Figura 4.5 (a), correspondente a 2θ = 1.58 é de difícil visualização em escala linear, ou mesmo quando os pontos dessa curva são postos em escala
logarítmica para a intensidade. Esse pico torna-se mais proeminente e definido somente quando
o ampliamos localmente, mesmo assim optamos pela escala linear, pois na ampliação perdemse as informações sobre os outros picos encontrados na curva. No gráfico (b) a curva bem
definida, sem ruídos e com picos proeminentes, a espessura para esse nanofilme é de d = 33.690
nanômetros.
4.2 DIFRAÇÃO POR RAIOS-X
(a) Amostra AlN sobre silício a 3 horas.
63
(b) Amostra AlN sobre vidro a 5 horas.
Figura 4.6 Difratogramas a baixos ângulos obtidos em Santa Maria, onde temos em (a) AlN sobre silício
depositado durante 3 horas e em (b) AlN sobre vidro depositado durante 5 horas.
Os gráficos da Figura 4.6 foram obtidos na (UFSM-LMMM), para as mesmas amostras
exibidas na Figura 4.5. Temos para a amostra deposita em 3 horas sobre silício, gráfico (a),
a espessura de d = 10.925 nanômetros, e para a amostra depositada em 5 horas sobre vidro,
gráfico (b), uma espessura de d = 35.458 nanômetros, essas espessuras foram obtidas usando-se
o mesmo método adotado na Figura 4.5.
Para as amostras depositadas em vidro com tempo de 10 horas não foram encontrados picos
nos difratogrmas a baixos ângulos, tanto na (UFSM-LMMM) quanto em (UFRN-DFTE), como
mostrado na Figura 4.7.
Figura 4.7 Difratograma a baixo ângulo para o nitreto de alumínio sobre o vidro depositado durante 10
horas, difratogrma (UFSM-LMMM).
64
4.3 MICROSCOPIA DE FORÇA ATÔMICA (AFM)
A taxa de deposição é calculada dividindo-se a espessura do nanofilme "d"pelo tempo de
deposição. A Tabela 4.2 abaixo mostra os resultados encontrados para as espessuras e as respectivas taxas de deposições.
Difratogramas Nanofilmes (UFRN)
Espessuras Taxas de deposições
Nitreto de Alumínio sobre silício - 3h de deposição
12,833 nm
1,188x10−3 nm/s
Nitreto de Alumínio sobre vidro - 5h de deposição
33,690 nm
1.871x10−3 nm/s
Difratogramas Nanofilmes (UFSM)
Espessuras Taxas de deposições
Nitreto de Alumínio sobre silício - 3h de deposição
10,925 nm
1,011x10−3 nm/s
Nitreto de Alumínio sobre vidro - 5h de deposição
35,458 nm
1.969x10−3 nm/s
Tabela 4.2 Espessuras e taxas de deposições, obtidos por raios-x a baixos ângulos.
4.3
Microscopia de Força Atômica (AFM)
A análise dos nanofilmes por microscopia de força atômica foi realizada no departamento
de Física da Universidade Federal de Pernambuco (UFPE-CCEN). As espessuras e consequentemente as taxas de deposição foram obtidas utilizando os seguintes equipamentos: microscópio de força atômica modelo Pico Scan 2500 do fabricante Molecular Imaging o modelo 5500 da Agilent Technologies, as imagens foram obtidas por modo Tapping utilizando
cantilevers de 225 um de comprimento, freqüência de ressonância de 190 khz e constante de
mola de 48N/m ( Modelo NCLR da Nanoworld). Foram obtidas imagens de 512x512 pixels
com uma velocidade de 0, 5 linhas/segundo. A Tabela 4.3 abaixo sintetiza os resultados encontrados.
Nanofilme
Espessura Média Taxa de deposição
Nitreto de Alumínio sobre vidro - 3h de deposição
16,600 nm
1,537x10−3 nm/s
Nitreto de Alumínio sobre vidro - 5h de deposição
33,290 nm
1.849x10−3 nm/s
Tabela 4.3 Espessuras e taxas de deposições, obtidos por microscopia de força atômica.
4.4 ESPECTROSCOPIA RAMAN
4.4
65
Espectroscopia Raman
As medidas de espalhamento Raman apresentadas nessa dissertação foram realizadas no
Laboratório de Espectroscopia Raman da UFC, usando o retroespalhamento de um feixe laser
com λ = 532 nm emitido de um laser de estado sólido modelo Verdi, da Coherent Inc., cuja
potência de saída foi fixada em 150 mW.
Entretanto, a potência incidente sobre as amostras é estimada entre 15 e 20 mW. A luz espalhada é coletada pelo sistema T64000 da Jobin Yvon-SPEX, Division d’Instruments S.A., ver
Figura 4.8, que consiste de um espectrômetro triplo, ao qual foi acoplado um sistema de microanálise, um micro-computador e um sistema de detecção tipo CCD (Coupled Charge Device).
A este conjunto de equipamentos chamamos de micro-Raman. O sistema de micro-análise
é constituído por uma câmera de vídeo ligada a um monitor e adaptada a um microscópio
Olympus BX40 com objetivas plano cromáticas e de foco ajustável. Este sistema permite focalizar o feixe do laser sobre a superfície da amostra com bastante precisão.
Figura 4.8 Espectrômetro T64000 da Jobin Yvon-SPEX, Division d’Instruments S.A. com seu sistema
de micro-análise.
4.4.1
Espectro Raman do Alvo e Modos de Vibração
O espectro Raman da Figura 4.10, é do alvo nitreto de alumínio (AlN), utilizado na deposição dos nanofilmes deste trabalho. Os índices em cima dos picos que caracterizam esse material
são devidos aos modos de vibração, onde temos:
A1 (TO) polarizção óptica transversal na direção z, A1 (LO) polarizção óptica longituninal
na direção z, E1 (TO) polarizção óptica transversal no plano (x, y) e E1 (LO) polarizção óptica
66
4.4 ESPECTROSCOPIA RAMAN
longituninal no plano (x, y) são modos Raman e infravermelho ativos. Por fim o modo E22
também é Raman ativo [70].
Figura 4.9 Espectro Raman para o nitreto de alumínio puro.
O espectro vibracional Raman do AlN tem sido objeto de intenso estudo nos últimos anos,
tanto por métodos experimentais quanto métodos teóricos. Entretanto um completo conhecimento das linhas Raman e seus modos ativos ainda não foi totalmente alcançado. Na Tabela
4.4, temos alguns valores experimentais e teóricos atribuídos aos modos ativos para o AlN.
–
A1 (LO)
A1 (TO)
Carlone
663
Collins
916
668
Bra f man
910
Davydov
Davydov*
E1 (LO) E1 (TO)
E22
303
426
821
614
667
910
667
890
611
912
670
248
657
881
615
922
673
252
667
607
924
241
660
252
660
241
660
301
704
Perlin
McNeil
893
614
916
673
San jur jo
888
659
895
671
607
924
668
989
Perlin
Ruiz∗
E21
899
734
665
Tabela 4.4 Valores experimentais e teóricos∗ obtidos para os modos ativos Raman em AlN [71].
A Tabela4.4 mostra a diferença entre os valores atribuidos aos modos ativos do AlN. Em
Ruiz∗ , os valores são teóricos, e foram obtidos usando o método Ab initio, aproximação HartreeFock-Roothan, através do programa CRYSTAL-92 [71].
4.4 ESPECTROSCOPIA RAMAN
4.4.2
67
Espectro Raman das Amostras AlN
Na Figura 4.10, temos os espectros Raman das amostras medidas.
Figura 4.10 Espectro Raman para as amostras do nitreto de alumínio.
Os modos de excitação Raman encontrados nos gráficos são:
Para as amostras depositadas em vidro com tempo de 3 horas, temos λ = 651 cm−1 . Esse
valor pode ser atribuido ao modo E22 deslocado, segundo a notação usada no espectro do nosso
alvo, ver Figura 4.10, ou ao modo deslocado A1 (TO), segundo Sanjurjo, ver Tabela 4.4. Para as
amostras depositadas em silício com tempo de 5 horas, temos, λ = 910 cm−1 . Esse valor pode
ser atribuido ao modo E1 (LO) deslocado, segundo a notação usada no espectro do nosso alvo,
ver Figura 4.10, ou exatamente aos modos A1 (LO) e E1 (LO), segundo Brafman, ver Tabela 4.4.
Para as amostras depositadas em vidro com tempo de 5 horas, temos, λ = 916 cm−1 . Esse
valor pode ser atribuido ao modo E1 (LO) deslocado, segundo a notação usada no espectro do
nosso alvo, ver Figura 4.10, ou exatamente aos modos A1 (LO), segundo Collins, ou E1 (LO),
4.4 ESPECTROSCOPIA RAMAN
68
segundo McNeil, ver Tabela 4.4. Para as amostras depositadas em vidro com tempo de 10 horas,
temos λ = 651 cm−1 . Esse valor pode ser atribuido ao modo E22 deslocado, segundo a notação
usada no espectro do nosso alvo, ver Figura 4.10, ou ao modo deslocado A1 (TO), segundo
Sanjurjo, ver Tabela 4.4.
Os modos de excitação ativos dos gráficos Raman das amostras, têm baixa intensidade,
possivelmente devido as pequenas espessura dos nanofilmes, tornando difícil a detecção por
espectroscopia Raman.
69
CONSIDERAÇÕES FINAIS
“Se o conhecimento pode criar problemas, não é através
da ignorância que podemos solucioná-los.”
—ISAAC ASIMOV (1920-1992)
Esta dissertação descreve o procedimento de crescimento e de caracterização dos nanofilmes semicondutores de nitreto de alumínio, utilizando a técnica Magnetron Sputtering de
Rádio-frequência não reativo.
Na caracterização utilizando raios-X, foi analisado os difratogramas do alvo, concluindo
através dos picos de difração que caracteriza o nitreto de alumínio, que o alvo é apropriado para
deposição dos nanofilmes. Porém os difratogramas das amostras revelou que os filmes não são
cristalinos, evidenciando o caráter amorfo das amostras. Através da análise dos raios-X a baixos
ângulos obtemos a espessura de cada amostra com sua respectiva taxa de deposição. As taxas
obtidas são pequenas e variáveis. Atribuímos esse comportamento principalmente ao fator baixa
potência da fonte RF ( 50W ), e a elevada estabilidade das ligações Al-N (300kJ/mol) e Al-Al
(186kJ/mol). Os resultados obtidos através da técnica, microscopia de força atômica (AFM)
concordam com os obtidos usando a técnica de raios-X a baixos ângulos, tanto para as pequenas
taxas de deposição quanto em seu comportamento variável. A caracterização por espectroscopia
Raman evidenciou a existência de modos ativos nas amostras analisadas, contudo, alguns picos
têm baixa intensidade e/ou são deslocados/alargados quando comparados com os dados teóricos
e experimentais referentes ao AlN.
Nas próximas deposições iremos variar os tipos de substratos, pois como sabemos, a estrutura do substrato influência fortemente as propriedades do filme depositado durante a nucleação,
na fase de crescimento do filme. Outro fator que iremos dedicar maior atenção será a temperatura do substrato, através de tratamento térmico dos nanofilmes depositados, utilizando a própria
câmara de deposição. Pois o processo de condensação se inicia nos primeiros momentos de formação do filme, pela formação de pequenos clustres (aglomerados), resultantes da combinação
de vários átomos adsorvidos, é influenciado pela temperatura do substrato. Calcularemos via
primeiros princípios os modos ativos Raman para o AlN, e com a chegada de uma nova fonte
RF de potência mais elevada poderemos obter nanofimes mais espersos, consequentemente mais
cristalinos.
A PÊNDICE A
Tabela Periódica
Figura A.1 Tabela Periódica.
70
APÊNDICE A TABELA PERIÓDICA
Figura A.2 Dados Referentes ao Nitreto de Alumínio.
71
72
Referências Bibliográficas
[1] FREIRE, Thatyara de Souza.; Crescimento de Filmes Nanométricos Monocristalinos de
Fe/MgO (100) por Sputtering DC. Dissertação de mestrado. Departamento de Física Experimental e Téorica. UFRN-DFTE. Natal-RN, Março de 2007.
[2] SPUTTERING.; Disponível em: <http://www-staff.lboro.ac.uk/ masdk/sputtering.html>.
Acesso em 7 de dezembro de 2010.
[3] THE OPTICAL THIN FILM DEPOSITION TECHNOLOGY. Thermal evaporation. Disponível em: <http://www.etafilm.com.tw/Thinfilm-filter-Deposition-History.html>. Acesso
em 2 de dezembro de 2010.
[4] PASCOALI, Suzy. Obtenção e Caracterização de Filmes de TiO2 Depositados Sobre Cerâmica de Revestimento Via Magnetron Sputtering DC. Tese de Doutorado. Ciência e Engenharia de Materiais. (UFSC) Florianópoles-Santa Catarina, Outubro de 2007.
[5] FILHO, Sebastião Eleutério. Magnetron Sputtering Planar Construção e Aplicação. Dissertação de Mestrado. Instituto de Física Gleb Wataghin. Universidade Estadual de campinasUNICAP. Campinas-SP, Abril de 1991.
[6] MATTOX, Donald M. Handbook of Physical Vapor Deposition (PVD) Processing: Film
Formation, Adhesion, Surface Preparation and Contamination Control. Published in the
United States of America by Noyes Publications 369 Fairview Avenue, Westwood, New
Jersey 07675, 1998.
[7] LUJAN, Guilherme Sansigolo. Filmes Finos de WN e AlN e suas Aplicações na Fabricação
de Transistores MESFET. Dissertação de Mestrado. Faculdade de Engenharia Elétrica e da
Computação. Universidade Estadual de campinas-UNICAP. Campinas-SP, Abril de 2000.
[8] BRUNDLE, C. Ricbard.; EVANS, Charles A.; WIHON, Jr.Sbaun. Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films. By Butxetworch-Heinemann, a
division of Reed Publishing USA. 1992.
[9] THERRY, L. Alford,; FELDMAN, Leonard C.; MAYER, James W.; Fundamentals of Nanoscale Film Analysis. Springer Science. Printed in the United States of America, 2007.
Library of Congress Control Number: 2005933265.
73
REFERÊNCIAS BIBLIOGRÁFICAS
[10] SPUTTERING, Physical Deposition. Disponível em: <http://knol.google.com/k/memsfabrication-process>. Acesso em 12 Agosto de 2010.
[11] SIGMUND, Peter. Theory of Sputtering. I. Sputtering Yield of Amorphous and Polycrystalline Targets. Phys. Review, Volume 184, Number 2, 10 August 1969.
[12] BURAKOWSKI, T.; WIERZCHONW, T. Surface Engineer of Metals Principles, Equipments and Technologies. New York, 1999.
[13] SESHAN, Krishna. Handbook of Thin-Film Deposition Processes and Techniques Principles, Methods, Equipment and Applications. Noyes Pubblications. William Andrew Publishing Norwich, New York, U.S.A. 2002.
[14] PLASMA.
Disponível
em:
wikipedia
a
enciclopédia
livre,
<http://pt.wikipedia.org/wiki/Plasma>. Acesso em 12 de agosto 2010.
[15] GALVÃO, RICARDO.; Física dos plasmas, Centro brasileiro de pesquisas fÍsica e Instituto de fÍsica-USP. Disponível em: <http://www.plasma.inpe.br/LAP/Sitio/Texto/FisicaBasica-de-Plasma.htm>. Acesso em 12 de agosto 2010.
[16] RICKERBY, D.S, MATTHEWS, A. Advanced surface coatings: A handbook of surface
engineering. Glasgow; Blackie and Son, 1991.
[17] R. Wendt, K. Ellmer, and K. Wiesemann. Thermal power at a substrate during ZnO: Al
thin film deposition in a planar magnetron sputtering system. J. Appl. Phys. 2115-2122,
1997.
[18] WASA, Kiyotaka.; MATSUSHITA, Makoto Kitabatake.; ADACHI, Hideaki.; Thin Film
Materials Technology Sputtering of Compound Materials. By William Andrew, Printed in
the United States 2004.
[19] CORRÊA, Marcio Assolin. Magnetoimpedância em Filmes Finemet/Metal/Finemet. Tese
de mestrado. Labortatório de Magnetismo e Materiais Magnéticos. UFSM-CCNE, Santa
Maria-RS, Outubro de 2004.
[20] SANCHES, C. de Oliveira. Crescimento e Caracterização de Filmes Finos de Óxido de
Si.Instrumentação ao Ensino. Instituto de Física Gleb Wataghin. Universidade Estadual de
Campinas. Campinas-SP, Junho de 2003.
[21] ANTON, R. Thin films and surfaces: heterogeneous nucleation and growth. Disponível
em: <http://wwwphysnet.uni-hamburg.de/iap/group-ds/research/nucleation.html>. Acesso
em 12 Agosto de 2010.
74
REFERÊNCIAS BIBLIOGRÁFICAS
[22] FREUND, L. B.; SURESH, S. Thin Film Materials Stress, Defect Formation and Surface
Evolution. Springer Science. Printed in the United States of America, 2003.
[23] HUAMAN, Noemi R. Checca. Crescimento de Fílmes nanométricos de Nitreto de Ferro e
Caracterização magnética, morfológica e elétrica. Dissertação de Mestrado. Departamento
de Física Experimental e Téorica. UFRN-DFTE. Natal-RN, Março de 2008.
[24] ALUMINÍO.
Origem,
Wikipédia,
a
enciclopédia
livre.
Disponível
em:
<http://pt.wikipedia.org/wiki/Aluminio>. Acesso em 7 de dezembro de 2010.
[25] ATKINS, Peter.; Loretta Jones. Princípios de química: questionando a vida moderna e o
meio ambiente. Editora Bookman-Porto Alegre, 2006; Terceira Edição.
[26] ALUMINÍO,Tabela Periódica. Disponível em:< http://www.ptable.com/>. Acesso em 15
de Agosto 2010.
[27] RUSSEL, John Blair. Química Geral. Pearson Makron Books-São Paulo, 1994. Segunda
Edição, vol. 2.
[28] TABLE,
Hazardous
Periodic
Materials
Table
of
News,
Elements.
Careers
Environmental,
and
Resources.
Chemistry
and
Disponível
em:
<http://environmentalchemistry.com/yogi/periodic/Al.html>. Acesso em 15 de Agosto
2010.
[29] MAHAN, Bruce M.; MYERS, Rollie J. Química Um Curso Universitário. Editora
Blücher-São Paulo, 1995; Quarta Edição.
[30] NITROGÊNIO,Tabela Periódica. Disponível em:< http://www.ptable.com/>. Acesso em
15 de Agosto 2010.
[31] TABLE,
Hazardous
Periodic
Materials
Table
of
News,
Elements.
Careers
Environmental,
and
Resources.
Chemistry
and
Disponível
em:
<http://environmentalchemistry.com/yogi/periodic/N.html>. Acesso em 15 de Agosto
2010.
[32] AUGER, M.A.; VÁZQUEZ, L.; JERGEL, M.; SÁNCHEZ O.; ALBELL, J.M. Structure
and Morphology Evolution of ALN Films Grown by DC Sputtering. Surface and Coatings
Technology 180-181 (2004) 140-144.
[33] KAR, J.P.; BOSE, G.; TULI, S. Effect of Annealing on DC Sputtered Aluminum Nitride
Films. Surface and Coatings Technology 198 (2005) 64-67.
[34] JEFFEREY, G. A.; PANY G. S.; J. Chem. Phys. 23(1-6) 406.
REFERÊNCIAS BIBLIOGRÁFICAS
75
[35] MANASREH, M.O. III-Nitride Semiconductor: Electrical, Structural and Defects Properties. Elsevier Science B. V. 2000.
[36] OLIVEIRA, Ivo de Castro. Estudo das Propriedades de Filmes Finos de Nitreto de Alumínio Produzidos por Processo de Magnetron Sputtering em Regimes contínuos (DC) e
Alternados (RF). Tese de Doutorado. Instituto de Tecnológico de Aeronáutica, 2004.
[37] ZHE, Chuan Feng. III-NITRIDE Semiconductor Materials. Published by Imperial College
Press.National Taiwan University, Taiwan 2006.
[38] ROENTGEN, W. Conrad. Disponível em: <http://www.medicinaintensiva.com.br/roentgen.htm>.
Acesso em 5 de Dezembro 2010.
[39] MARTINS, R. A. A Descoberta dos Raios X: O primeiro comunicado de Röntgen. Revista
Brasileira de Ensino de Física. 20, 373-391 (1998).
[40] BLEICHER, Lucas; SASAKI, José M. Introdução à Difração de Raios-X em Cristais.
UFC, Ceará-Fortaleza, 2000.
[41] BIOGRAFIAS, Sala de Física. Disponível em: <www.saladefisica.cjb.net>. Acesso em 15
Agosto 2010.
[42] SUASSUNA, José F. Notas de Aula: Física do Estado Sólido III, Difração de Raios-X em
Cristais e Teoria da Rede Recíproca. UFCG-Campina Grande-Pb, Agosto-2007, Centro de
Ciências e Tecnologia. Unidade Acadêmica Física-Campus II.
[43] TÉCNICAS, Autor desconhecido. Algumas Técnicas de Caracterização de Materiais.
Disponível em: <www.foz.unioeste.br/ lamat/downmateriais/materiaiscap5.pdf>. Acesso
em 15 Agosto 2010.
[44] CEDERJ, Fórum de discussão do Curso de Tecnologia em Sistemas de Computação. Disponível em: <http://www.compcederj.com.br/forum/viewtopic.php>. Acesso em 15 Agosto
2010.
[45] CALLISTEM, Jr. Willian D. Ciência e Engenharia de Materiais: Uma Introdução. Editora LTC, Rio de Janeiro, Sétima Edição. 2008.
[46] AZEVEDO, Walter Filgueira. Difração de Raios X. Laboratório de Sistemas Biomoleculares. Departamento de Física-Instituto de Biociências, Letras e Ciências. Exatas-UNESP,
São José do Rio Preto. SP.
[47] RAMAN, spectroscopy. Origem, Wikipédia, a enciclopédia livre. Disponível em:
<http://en.wikipedia.org/wiki/Raman-spectroscopy> Acesso em 7 de SETEMBRO de
2010.
76
REFERÊNCIAS BIBLIOGRÁFICAS
[48] O Efeito Raman, Origem: Seara da Ciência.Um Exemplo de Espectro Raman.Disponível
em: <http://seara.ufc.br/especiais/fisica/raman/raman.htm>. Acesso em 7 de Setembro de
2010.
[49] EISBERG, Robert.; RESNICK, Robert Física Quântica. Editora Elservier, Rio de Janeiro,
1979. Vigésima Oitava Edição.
[50] SALA, Oswaldo. Fundamentos da Espectroscopia Raman e no Infravermelho. Editora
UNESP-São Paulo, 2008; Segunda Edição.
[51] ESPECTRO,
Regiões
do
Espectro
Eletromagnético.;
Disponívem
em:
<http://www.df.ufscar.br/aula1.pdf>. Acesso em 7 de Setembro de 2010.
[52] Blogs
de
Ciência-Divulgação
de
todos
os
blogs
em
Português
que
ver-
sam a ciência. Parte do Projecto Divulgar a Ciência(.com). Disponível em:
<http://divulgarciencia.com/categoria/luz/page/>. Acesso em 7 de Setembro de 2010.
[53] CARTER, Renata A.Bitar. Estudo do Técido Mamário Humano por Espectroscópia FTRaman. Dissertação de Mestrado. Universidade do Vale do Paraíba. Instituto de Pesquisa e
Desenvolvimento. Engenharia Biomédica. São José dos Campos-São Paulo, 2004.
[54] NAKAGOMI, Fábio. Efeitos da Distribuição da População de Cobalto e Magnésio nas Propriedades Estruturais e Magnéticas de Nanoparticulas de Cox Fe(3−x) Ox e
Mgx Fe(3−x) Ox . Dissertação de Mestrado. Instituto de Física, Universidade de Brasília. Setembro de 2008.
[55] LEITE, Cristiano Fantini. Estudo de Elétrons e Fônons em Nanotubos de Carbono por Espalhamento Raman Ressonante. Tese Doutorado. Departamento de Física da Universidade
Federal de Minas Gerais. Outubro de 2005.
[56] AMER, Maher S. Raman spectroscopy for soft matter applications. Published by John
Wiley and Sons, Inc., Hoboken, New Jersey. Printed in the United States of America, 2009.
[57] SMITH, Ewen.; DENT, Geoffrey. Modern Raman spectroscopy: a practical approach.
John Wiley and Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, England.
2005.
[58] Dispositivo de carga acoplada.; Origem, Wikipédia, a enciclopédia livre. Disponível em:
<http://pt.wikipedia.org/wiki/Dispositivo-de-carga-acoplada>. Acesso em 27 outubro de
2010.
[59] McCreery, Richard L. Raman spectroscopy for chemical analysis. By a John Wiley And
Sons. Printed in the United States of America, 2000.
REFERÊNCIAS BIBLIOGRÁFICAS
77
[60] MAFRA, Daniela LopeS. Dispersão de fônons na vizinhança do ponto de Dirac do grafeno por espalhamento Raman. Dissertação de Mestrado. Universidade Federal de Minas
Gerais. Belo Horizonte-MG, Julho de 2008.
[61] MACIEL, Indhira Oliveira. Estudo de dopagem em nanotubos de carbono por espectroscopia Raman ressonante. Tese de Doutorado. Universidade Federal de Minas Gerais. Belo
Horizonte-MG, Maio de 2009
[62] SALA, Oswaldo. Uma Molécula Didática. Quim. Nova, Vol. 31, No. 4, 914-920, 2008.
[63] ZIMAN, John M. Principles of The Theory of Solids.Cambridge University Press,1979.
[64] REZENDE, Sergio M. Materiais e Dispositivos Eletrônicos. Editora Livraria da FísicaSão Paulo, 2004; Segunda Edição.
[65] BINNING, G., F. Quate, Ch. Gerber, Physical Review Letters, v. 56, p.930, (1986).
[66] TERRIS, B. D., Physical Review Letters. v. 63, p. 2669-2672.
[67] BINNING, G, and Heinrich Rohrer Rev. Mod. Phys. v. 59, p. 615-625. (1987).
[68] GONÇALVES,Charlie Salvador. Propriedades Físicas do Monocristal Fe/MgO(100) e
Estudo da Expansão Térmica da Superfície da Ag(100). Tese de Doutorado. Departamento
de Física Experimental e Téorica. UFRN-DFTE. Natal-RN, Março de 2010.
[69] FEWSTER, Paul F Fewster. X-ray analysis of thin films and multilayers. Rep. Prog. Phys.
59 (1996) 1339-1407. Printed in the UK.Received 11 June 1996.
[70] XIAOJUN, Li; ZHOUB, Candong; JIANG, Guochang; YOU, Jinglin. Raman Analysis of
Aluminum Nitride at High Temperature. Materials Characterization 57 (2006) 105-110.
[71] RUIZ, Elisseo.; ALVAREZ, Santiago. Electronic Structure and Properties of AlN. Phys.
Rev. B 49, Number 11.15 March 1994.
[72] OLIVEIRA, Ivan S.; Vitor L. B. de Jesus. Introdução à Física do Esatdo Sólido. Editora
Livraria da Física-São Paulo,2005; Primeira Edição.
[73] ASHCROFT, Neil W.; MERMIM, N. David. Solid State Physics. Thomson LearningUSA,1976; Brooks/Cole (College Edition).
[74] KITEL, Charles. Introdução a Física do Estado Sólido. Editora LTC, Rio de Janeiro 2006.
Tradução da Oitava Edição.
[75] MELO, Hilton Andrade de.; BIASI, Ronaldo Sérgio de, Introdução à Física dos Semicondutores. Editora Edgard Blücher, Instituto Nacional do Livro. Brasília 1975.
REFERÊNCIAS BIBLIOGRÁFICAS
78
[76] PERKOWITZ, Sidney. Optical Characterization Semiconducors: Infrared, Raman, and
Photoluminescence Spectroscopy. Acacademic Press Limited, United States Edition. Second Printing 1994.
[77] CARLONE, C.; LAKIN, K.M.; SHANKS, H. R. Opitical Phonons of Aluminum Nitride.
J. Appl. Phys. 55(11), 1 June 1984.
[78] RUIZ, Eliseo; ALVAREZ, Santiago. Electronic Structure and Properties of AlN. Pysical
Review B, Volume 49, Number 11. 15 March 1994.
[79] LIU, M. S.; NUGENT, K.W.; PRAWER, S.; BUSILL, L.A.; PENG, J.L.; TONG Y.Z. and
JEWSBURY, P.; Micro-Raman Scattering Properties of Highly Oriented AlN Films. Int.
Mod. Phys. 12(1998) 1963.