Termometria e Calorimetria

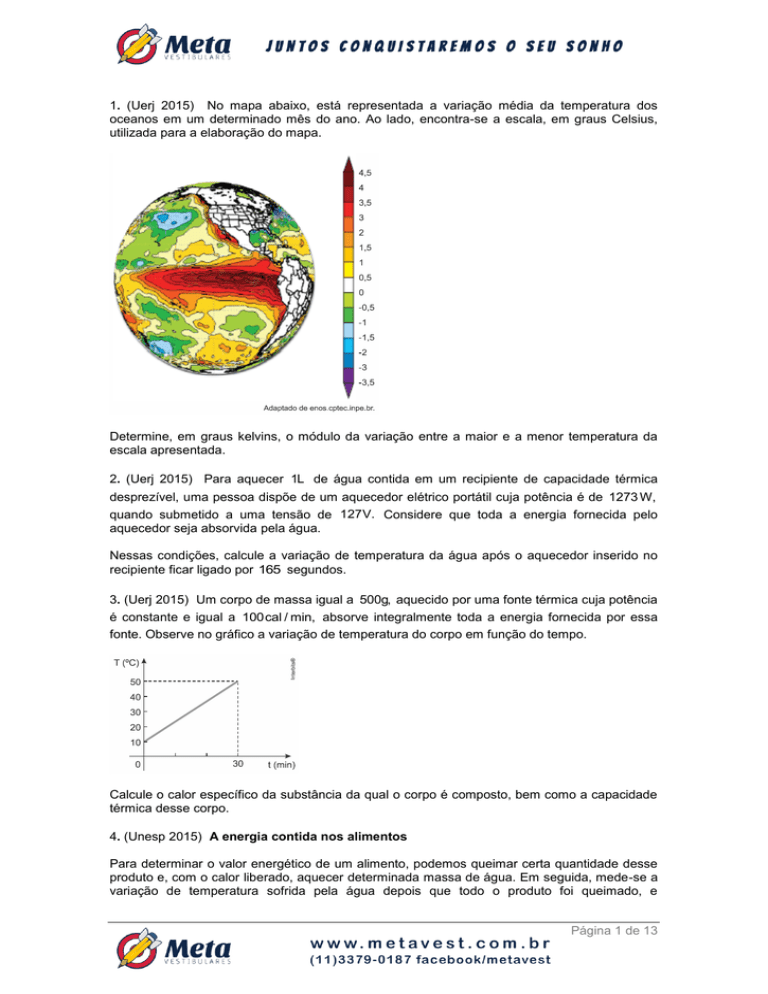
1. (Uerj 2015) No mapa abaixo, está representada a variação média da temperatura dos
oceanos em um determinado mês do ano. Ao lado, encontra-se a escala, em graus Celsius,
utilizada para a elaboração do mapa.
Determine, em graus kelvins, o módulo da variação entre a maior e a menor temperatura da
escala apresentada.
2. (Uerj 2015) Para aquecer 1L de água contida em um recipiente de capacidade térmica
desprezível, uma pessoa dispõe de um aquecedor elétrico portátil cuja potência é de 1273 W,
quando submetido a uma tensão de 127V. Considere que toda a energia fornecida pelo
aquecedor seja absorvida pela água.
Nessas condições, calcule a variação de temperatura da água após o aquecedor inserido no
recipiente ficar ligado por 165 segundos.
3. (Uerj 2015) Um corpo de massa igual a 500g, aquecido por uma fonte térmica cuja potência
é constante e igual a 100cal / min, absorve integralmente toda a energia fornecida por essa
fonte. Observe no gráfico a variação de temperatura do corpo em função do tempo.
Calcule o calor específico da substância da qual o corpo é composto, bem como a capacidade
térmica desse corpo.
4. (Unesp 2015) A energia contida nos alimentos
Para determinar o valor energético de um alimento, podemos queimar certa quantidade desse
produto e, com o calor liberado, aquecer determinada massa de água. Em seguida, mede-se a
variação de temperatura sofrida pela água depois que todo o produto foi queimado, e
Página 1 de 13
determina-se a quantidade de energia liberada na queima do alimento. Essa é a energia que tal
alimento nos fornece se for ingerido.
No rótulo de um pacote de castanha de caju, está impressa a tabela a seguir, com informações
nutricionais sobre o produto.
INFORMAÇÃO NUTRICIONAL
Porção 15 g
Quantidade por porção
90 kcal
Valor energético
Carboidratos
4,2 g
Proteínas
3g
Gorduras totais
7,3 g
Gorduras saturadas
1,5 g
Gordura trans
0g
Fibra alimentar
1g
Sódio
www.brcaju.com.br
45 g
Considere que 150 g de castanha tenham sido queimados e que determinada massa m de
água, submetida à chama dessa combustão, tenha sido aquecida de 15 C para 87 C.
Sabendo que o calor específico da água líquida é igual a 1cal (g  C) e que apenas 60% da
energia liberada na combustão tenha efetivamente sido utilizada para aquecer a água, é
correto afirmar que a massa m, em gramas, de água aquecida era igual a
a) 10000.
b) 5000.
c) 12500.
d) 7500.
e) 2500.
5. (Ufsm 2015) Um dos métodos de obtenção de sal consiste em armazenar água do mar em
grandes tanques abertos, de modo que a exposição ao sol promova a evaporação da água e o
resíduo restante contendo sal possa ser, finalmente, processado. A respeito do processo de
evaporação da água, analise as afirmações a seguir.
I. A água do tanque evapora porque sua temperatura alcança 100C.
II. Ao absorver radiação solar, a energia cinética de algumas moléculas de água aumenta, e
parte delas escapa para a atmosfera.
III. Durante o processo, linhas de convecção se formam no tanque, garantindo a continuidade
do processo até que toda a água seja evaporada.
Está(ão) correta(s)
a) apenas I.
b) apenas II.
c) apenas III.
d) apenas I e II.
e) I, II e III.
TEXTO PARA A PRÓXIMA QUESTÃO:
Recentemente, uma equipe de astrônomos afirmou ter identificado uma estrela com dimensões
comparáveis às da Terra, composta predominantemente de diamante. Por ser muito frio, o
astro, possivelmente uma estrela anã branca, teria tido o carbono de sua composição
cristalizado em forma de um diamante praticamente do tamanho da Terra.
Página 2 de 13
6. (Unicamp 2015) Os cálculos dos pesquisadores sugerem que a temperatura média dessa
estrela é de Ti  2.700 C. Considere uma estrela como um corpo homogêneo de massa
M  6,0  1024 kg constituída de um material com calor específico c  0,5 kJ / (kg C). A
quantidade de calor que deve ser perdida pela estrela para que ela atinja uma temperatura final
de Tf  700 C é igual a
a) 24,0  1027 kJ.
b) 6,0  1027 kJ.
c) 8,1 1027 kJ.
d) 2,1 1027 kJ.
7. (Pucrs 2014) Uma forma de aquecer água é usando aquecedores elétricos de imersão,
dispositivos que transformam energia elétrica em energia térmica, mediante o uso de resistores
elétricos. Um desses aquecedores, projetado para fornecer energia na razão de 500 calorias
20 C
por segundo, é utilizado no aquecimento de 500 gramas de água, da temperatura de
80 C.
para
Considerando que toda a energia transferida é aproveitada no aquecimento da
c  1,0 cal / g  C,
água e sabendo que o calor específico da água é
o tempo necessário para
80 C
atingir
é igual a
a) 60 s
b) 68 s
c) 75 s
d) 84 s
e) 95 s
8. (Acafe 2014) Largamente utilizados na medicina, os termômetros clínicos de mercúrio
relacionam o comprimento da coluna de mercúrio com a temperatura. Sabendo-se que quando
a coluna de mercúrio atinge 2,0cm, a temperatura equivale a 34°C e, quando atinge 14cm, a
temperatura equivale a 46°C. Ao medir a temperatura de um paciente com esse termômetro, a
coluna de mercúrio atingiu 8,0cm.
A alternativa correta que apresenta a temperatura do paciente, em °C, nessa medição é:
a) 36
b) 42
c) 38
d) 40
9. (Uea 2014) Um turista estrangeiro leu em um manual de turismo que a temperatura média
do estado do Amazonas é de 87,8 graus, medido na escala Fahrenheit. Não tendo noção do
que esse valor significa em termos climáticos, o turista consultou um livro de Física,
encontrando a seguinte tabela de conversão entre escalas termométricas:
fusão do gelo
ebulição da água
Celsius
0
100
Fahrenheit
32
212
Com base nessa tabela, o turista fez a conversão da temperatura fornecida pelo manual para a
escala Celsius e obteve o resultado:
a) 25.
b) 31.
c) 21.
d) 36.
e) 16.
10. (G1 - ifce 2014) Ao tomar a temperatura de um paciente, um médico do programa Mais
Médicos só tinha em sua maleta um termômetro graduado na escala Fahrenheit. Após colocar
Página 3 de 13
o termômetro no paciente, ele fez uma leitura de 104°F. A correspondente leitura na escala
Celsius era de
a) 30.
b) 32.
c) 36.
d) 40.
e) 42.
11. (Unesp 2014) Para testar os conhecimentos de termofísica de seus alunos, o professor
propõe um exercício de calorimetria no qual são misturados 100 g de água líquida a 20 °C com
200 g de uma liga metálica a 75 °C. O professor informa que o calor específico da água líquida
é 1 cal /  g  C e o da liga é 0,1 cal /  g  X, onde X é uma escala arbitrária de temperatura,
cuja relação com a escala Celsius está representada no gráfico.
Obtenha uma equação de conversão entre as escalas X e Celsius e, considerando que a
mistura seja feita dentro de um calorímetro ideal, calcule a temperatura final da mistura, na
escala Celsius, depois de atingido o equilíbrio térmico.
12. (Uel 2014) Uma gota de álcool de 10 g, à temperatura de 70 °C, cai em um reservatório
com 1000 litros de água a 33 ºC.
Dados: Calor específico da água: 1,0 cal/g °C
Calor específico do álcool: 0,6 cal/g °C
Massa específica da água: 1000 kg/m 3
a) Calcule a quantidade de calor transferida para a água.
b) Calcule a variação de entropia do reservatório de água. Sabendo que ΔS  0, o que se pode
concluir da entropia da gota de álcool?
Apresente os cálculos.
13. (G1 - cps 2014) Quem viaja de carro ou de ônibus pode ver, ao longo das estradas, torres
de transmissão de energia tais como as da figura.
Página 4 de 13
Olhando mais atentamente, é possível notar que os cabos são colocados arqueados ou, como
se diz popularmente, “fazendo barriga”.
A razão dessa disposição é que
a) a densidade dos cabos tende a diminuir com o passar dos anos.
b) a condução da eletricidade em alta tensão é facilitada desse modo.
c) o metal usado na fabricação dos cabos é impossível de ser esticado.
d) os cabos, em dias mais frios, podem encolher sem derrubar as torres.
e) os ventos fortes não são capazes de fazer os cabos, assim dispostos, balançarem.
14. (Pucrs 2014) O piso de concreto de um corredor de ônibus é constituído de secções de
20m separadas por juntas de dilatação. Sabe-se que o coeficiente de dilatação linear do
concreto é 12  106 C1, e que a variação de temperatura no local pode chegar a 50°C entre
o inverno e o verão. Nessas condições, a variação máxima de comprimento, em metros, de
uma dessas secções, devido à dilatação térmica, é
a) 1,0  102
b) 1,2  102
c) 2,4  104
d) 4,8  104
e) 6,0  104
15. (Udesc 2014) Certo metal possui um coeficiente de dilatação linear α. Uma barra fina
deste metal, de comprimento L0 , sofre uma dilatação para uma dada variação de temperatura
ΔT. Para uma chapa quadrada fina de lado L 0 e para um cubo também de lado L0 , desse
mesmo metal, se a variação de temperatura for 2ΔT, o número de vezes que aumentou a
variação da área e do volume, da chapa e do cubo, respectivamente, é:
a) 4 e 6
b) 2 e 2
c) 2 e 6
d) 4 e 9
e) 2 e 8
16. (Fuvest 2014) Uma lâmina bimetálica de bronze e ferro, na temperatura ambiente, é fixada
por uma de suas extremidades, como visto na figura abaixo.
Página 5 de 13
Nessa situação, a lâmina está plana e horizontal. A seguir, ela é aquecida por uma chama de
gás. Após algum tempo de aquecimento, a forma assumida pela lâmina será mais
adequadamente representada pela figura:
Note e adote:
O coeficiente de dilatação térmica linear do ferro é 1,2  105 C1.
O coeficiente de dilatação térmica linear do bronze é 1,8  105 C1.
Após o aquecimento, a temperatura da lâmina é uniforme.
a)
b)
c)
d)
e)
17. (Ufg 2014) Uma longa ponte foi construída e instalada com blocos de concreto de 5 m de
comprimento a uma temperatura de 20°C em uma região na qual a temperatura varia ao longo
do ano entre 10°C e 40°C. O concreto destes blocos tem coeficiente de dilatação linear de 10 5°C-1. Nessas condições, qual distância em cm deve ser resguardada entre os blocos na
instalação para que, no dia mais quente do verão, a separação entre eles seja de 1 cm?
a) 1,01
b) 1,10
c) 1,20
d) 2,00
e) 2,02
18. (Ifsc 2014) Em uma atividade experimental, o professor de Física pede para que seus
alunos adicionem 40 g de gelo a -10 °C em um calorímetro ideal, que contém uma quantidade
de água a 80 °C. Quando o sistema atinge o equilíbrio térmico, é observado que 25% do gelo
continua boiando. Sabendo que o calor específico da água é 1 cal/g°C e que do gelo é 0,5
cal/g°C, que o calor latente de fusão do gelo é 80 cal/g, assinale a soma da(s) proposição(ões)
CORRETA(S).
01) O calorímetro em questão participa das trocas de calor, influenciando na temperatura final
de equilíbrio térmico.
02) A quantidade de calor cedido pela água não foi igual à quantidade de calor recebido pelo
gelo, pois não foi suficiente para fundi-lo totalmente.
04) A temperatura de equilíbrio térmico do sistema é 0 °C.
08) A dilatação anômala da água tem influência direta na temperatura final de equilíbrio térmico
do sistema.
16) A massa inicial de água no calorímetro é 32,5 g.
32) Para que a temperatura final de equilíbrio seja de 10 °C, uma possibilidade é mudar a
quantidade inicial de água no calorímetro para aproximadamente 54,2 g.
Página 6 de 13
19. (Uerj 2014) Observe na tabela os valores das temperaturas dos pontos críticos de fusão e
de ebulição, respectivamente, do gelo e da água, à pressão de 1 atm, nas escalas Celsius e
Kelvin.
Pontos críticos
Fusão
Ebulição
Temperatura
°C
K
0
273
100
373
Considere que, no intervalo de temperatura entre os pontos críticos do gelo e da água, o
mercúrio em um termômetro apresenta uma dilatação linear.
Nesse termômetro, o valor na escala Celsius correspondente à temperatura de 313 K é igual a
a) 20
b) 30
c) 40
d) 60
20. (Uerj 2014) A energia consumida por uma pessoa adulta em um dia é igual a 2 400 kcal.
Determine a massa de gelo a 0°C que pode ser totalmente liquefeita pela quantidade de
energia consumida em um dia por um adulto. Em seguida, calcule a energia necessária para
elevar a temperatura dessa massa de água até 30°C.
Página 7 de 13
Gabarito:
Resposta
da
questão
1:
As variações de temperatura nas escalas Celsius (θ) e Kelvin (T) são numericamente iguais.
Δθ  4,5   3,5   8 °C 
ΔT  8 K.
Resposta
da
questão
Dados: P  1.273 W; V  1 L  m  1.000 g; Δt  165 s; c  4,2 J/g  °C.
Q  m c ΔT


Q
 Q  PΔt
P 
Δt

 m c ΔT  P Δ t
 ΔT 
2:
P Δ t 1.273  165


m c 1.000  4,2
ΔT  50 °C.
Resposta
da
Dados: m  500 g; P  100 cal/min.
Q  m c ΔT


Q
 Q  PΔt
P 
Δt

 m c ΔT  P Δ t
questão
 c
3:
100  30 
PΔt


m ΔT 500  50  10 
c  0,15 cal/g  °C.
C  m c  500  0,15  
Resposta
[D]
C  75 cal/°C.
da
questão
4:
Em 150 g de castanha temos 10 porções. Portanto, da tabela, a energia liberada nessa queima
é:
E  10  90  900 kcal  E  900.000 cal.
Como somente 60% dessa energia são usados no aquecimento da água, aplicando a equação
do calor sensível, temos:
0,6 E 0,6  900.000
Q  m c Δθ  0,6 E  m c Δθ  m 


c Δθ
1  87  15 
m  7.500 g.
Resposta
[B]
da
questão
5:
Justificando as incorretas:
[I] Incorreta. A evaporação é um processo de vaporização que ocorre abaixo da temperatura
de ebulição.
[II] Correta.
[III] Incorreta. Não ocorre convecção porque a água quente, menos densa, está na superfície,
não realizando movimento descendente.
Página 8 de 13
Resposta
[B]
da
questão
6:
Q  M c Δθ  6  1024  0,5  700  2.700  Q  6  1027 kJ.
Resposta
[A]
da
questão
7:
Dados: θ0  20C; θ  80C; m  500 g; P  500 cal / s; c  1 cal / g  C.
Aplicando a definição de potência:
P
Q
Q m c Δθ 500  1  80  20 
 Δt  

Δt
P
P
500
Resposta
[D]

Δt  60 s.
da
questão
8:
questão
9:
Fazendo a correspondência entre as escalas:
T  34
82
T  34
6



 t  34  6 
46  34 14  2
12
12
T  40 C
Resposta
[B]
da
5  55,8 
θC  0
θC
F  32
87,8  32



 θC 

100  0 212  32
100
180
9
Resposta
[D]
da
θC  31 C.
questão
10:
Fazendo a conversão:
θC θF  32

5
9

θC 104  32

5
9
Resposta

θC 72

5
9
 θC  40 °C.
da
questão
11:
3
Dados: mA  100 g; mL  200 g; c A  1 cal / g  C; kg / m ; cL  0,1 cal / g  X  0,6 cal / g  C.
– Equação de conversão entre as escalas.
Com os valores do gráfico:
 X  25 θC  0
 X  25 C




85  25 10  0
60
10
X  6 C  25 .
– Temperatura de Equilíbrio 
Ainda do gráfico:
ΔX ΔC

 ΔX  6 ΔC .
60
10
Página 9 de 13
Enquanto a marca do mercúrio sobe 1 grau na escala Celsius, sobe 6 graus na escala X,
conforme ilustra a figura.
Então o calor específico da liga é seis vezes maior quando expresso usando a escala
Celsius. Assim:
cL  6  (0,1 cal / g  C)  0,6 cal / g  C
Fazendo o somatório dos calores trocados para um sistema termicamente isolado:
Qágua  Q Liga  0   m c Δθ Água   m c Δθ Liga  0 
100 1 θ  20   200  0,6  θ  75   0 
θ  20  1,2 θ  90  0

2,2 θ  110 
θ  50 °C.
Resposta
da
questão
12:
Nota: muito estranho 1 gota ter massa 10 gramas. Não se pretende discutir, aqui, o conceito
de gota, mas, para a água, se aceita como padrão, 20 gotas ter massa 1 g.
a) Como a massa de água é muito maior que a massa de álcool, a temperatura de equilíbrio é
33 °C. Então a quantidade de calor perdida pela a gota é:
Qágua  Qgota  0  Qágua  -Qgott  -mgota cálcool Δθgota  -10  0,6  (33  70) 
Qágua  222 cal.
b) Como a transformação é irreversível, a variação da entropia do sistema é positiva
(ΔS  0).
ΔSsist  0  ΔSágua  ΔSálcool  0 
Q
Tágua
 ΔSálcool  0 
222
 ΔSálcool  0 
306
ΔSálcool  0,725 J/K.
Resposta
[D]
da
questão
13:
Nos dias frios, o comprimento dos fios diminui devido à contração térmica, daí a necessidade
de deixar uma folga entre cada duas torres, o que forma a barriga.
Resposta
[B]
da
questão
14:
Página 10 de 13
ΔL  L0 α Δθ  20  12  106  50 
Resposta
[B]
ΔL  1,2  102 m.
da
questão
15:
Para variações de temperatura ΔT e 2ΔT, as variações da área e do volume são:
ΔA1  A 0 2 α ΔT

ΔA 2  A 0 2 α  2 ΔT 

ΔA 2
 2.
ΔA1
ΔV1  V0 3 α ΔT

ΔV2  V0 3 α  2 ΔT 

ΔV2
 2.
ΔV1
Resposta
[D]
da
questão
16:
Coeficiente de dilatação linear do bronze é maior que o do ferro, portanto a lâmina de bronze
fica com comprimento maior, vergando como mostrado na alternativa [D].
Resposta
[B]
da
questão
17:
questão
18:
Dados: L0  5 m; α  105C1; Δθ  40  20  20 C.
ΔL  L0 α Δθ  5  105  20  103 m  0,1 cm.
d  1  0,1  d  1,10 cm.
Resposta
04 + 16 + 32 = 52.
da
[01] Incorreta, pois o calorímetro é ideal.
[02] Incorreta. Se há troca de calor apenas entre a água e o gelo, necessariamente a
quantidade de calor cedida por um é igual à quantidade de calor recebida pelo outro.
[04] Correta. No equilíbrio térmico há uma mistura de água e gelo sob pressão normal,
portanto a temperatura é 0 °C.
[08] Incorreta. O coeficiente de dilatação não altera o calor específico sensível, que é suposto
constante.
[16] Correta. Calculando a massa inicial da água:
A massa de gelo que funde (mf) corresponde a 75% da massa inicial (40 g).
mf  0,75  40  mf  30 g.
Fazendo o balanço térmico:
Qágua  Qgelo  Qfusão  0 
 m c Δθ água   m c Δθ gelo  mf L f fusão  0

m  1 0   80    40  0,5 0   10    30  80  0 
80 m  200  2.400  m 
2.600
80

m  32,5 g.
[32] Correta. Chamando de água1 a água contida inicialmente no calorímetro e de água2 a
Página 11 de 13
água resultante da fusão do gelo, façamos o novo balanço térmico.
Qágua1  Qgelo  Qfusão  Qágua2  0 
 m c Δθ água1   m c Δθ gelo  m L f fusão  m
c Δθ água2  0 
m  1 10   80    40  0,5 0   10    40  80  40  110  0   0 
70 m  200  3.200  400  m 
3.800
70

m  54,2 g.
Resposta
[C]
da
questão
19:
questão
20:
Da relação entre essas duas escalas:
TC  TK  273  313  273  TC  40 C.
Resposta
da
 Massa de gelo fundida:
Dados: Q = 2.400 kcal; Lf = 80 kcal/kg.
Da expressão do calor latente:
Q 2 400
Q  m Lf  m 

 m  30 kg.
Lf
80
 Energia para elevar até 30 °C:
Dados: m = 30 kg; c = 1 kcal/kg°C; Δθ  30C.
Da expressão do calor sensível:
Q  m c Δθ  Q  30  1 30  Q  900 kcal.
Página 12 de 13
Resumo das questões selecionadas nesta atividade
Q/prova Q/DB
Grau/Dif.
Matéria
Fonte
Tipo
1 ............. 136998 ..... Baixa ............. Física............. Uerj/2015 ............................. Analítica
2 ............. 137005 ..... Baixa ............. Física............. Uerj/2015 ............................. Analítica
3 ............. 136999 ..... Baixa ............. Física............. Uerj/2015 ............................. Analítica
4 ............. 135727 ..... Baixa ............. Física............. Unesp/2015.......................... Múltipla escolha
5 ............. 137463 ..... Baixa ............. Física............. Ufsm/2015............................ Múltipla escolha
6 ............. 135834 ..... Baixa ............. Física............. Unicamp/2015 ...................... Múltipla escolha
7 ............. 134598 ..... Baixa ............. Física............. Pucrs/2014 ........................... Múltipla escolha
8 ............. 132819 ..... Baixa ............. Física............. Acafe/2014 ........................... Múltipla escolha
9 ............. 133302 ..... Baixa ............. Física............. Uea/2014 ............................. Múltipla escolha
10 ........... 131676 ..... Baixa ............. Física............. G1 - ifce/2014 ...................... Múltipla escolha
11 ........... 132566 ..... Média ............ Física............. Unesp/2014.......................... Analítica
12 ........... 128920 ..... Média ............ Física............. Uel/2014............................... Analítica
13 ........... 130344 ..... Baixa ............. Física............. G1 - cps/2014 ...................... Múltipla escolha
14 ........... 131972 ..... Baixa ............. Física............. Pucrs/2014 ........................... Múltipla escolha
15 ........... 129636 ..... Média ............ Física............. Udesc/2014 .......................... Múltipla escolha
16 ........... 128409 ..... Baixa ............. Física............. Fuvest/2014 ......................... Múltipla escolha
17 ........... 128584 ..... Baixa ............. Física............. Ufg/2014 .............................. Múltipla escolha
18 ........... 133061 ..... Baixa ............. Física............. Ifsc/2014 .............................. Somatória
19 ........... 127302 ..... Baixa ............. Física............. Uerj/2014 ............................. Múltipla escolha
20 ........... 128659 ..... Baixa ............. Física............. Uerj/2014 ............................. Analítica
Página 13 de 13