genética de transmissão: ligação e mapas genéticos

GENÉTICA DE TRANSMISSÃO:
LIGAÇÃO E MAPAS GENÉTICOS
100
LIGAÇÃO, CROSSING-OVER E MAPEAMENTO GENÉTICO EM EUCARIONTES
INTRODUÇÃO
Neste capítulo, vamos falar um pouco de características genéticas, onde a 2ª
lei de Mendel ou lei da segregação independente não pode ser aplicada.
Como já vimos anteriormente, apesar de algumas características não
apresentarem as proporções mendelianas do di-hibridismo (interação gênica), os
pares de alelos que compõem essas características segregam-se, na hora de formar
os gametas, de forma independente. Isso acontece porque esses pares de alelos se
encontram em pares de cromossomo homólogos distintos, quando ocorre a
meiose, processo de formação de gametas. Na realidade, os pares de cromossomos
homólogos distintos é que se separam de forma independente levando junto os
alelos que neles estão distribuídos.
Porém
cada
par
de
cromossomos
homólogos possui uma grande quantidade de genes e esses genes na hora de
formar os gametas vão juntos com os cromossomos homólogos, como se fosse uma
única unidade (fig.4.1).
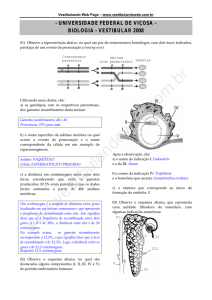
Figura 4.1: Representação esquemática da meiose. No lado direito, distribuição independente:
dois genes em dois pares de cromossomos homólogos diferentes. No lado esquerdo, ligação:
dois genes em um único par de homólogos; sem ocorrência de troca ou crossing-over. Fonte:
Klug et. al., 2010.
101
1. LIGAÇÃO, RECOMBINAÇÃO E CROSSING-OVER
Sutton e Boveri foram os primeiros, em 1903, a levantar a hipótese de que
cada cromossomo era constituído por mais de um gene ou “fator heredit|rio” e que
esses cromossomos no momento de formar os gametas levavam junto os genes.
Então, se os dois pares de alelos que determinam duas características distintas se
encontrarem em um mesmo par de cromossomos homólogos, esses alelos, na hora
da formação dos gametas, irão juntos no mesmo cromossomo, não segregando
independentemente.
Pares de alelos que determinam características diferentes, mas se
encontram em um mesmo par de cromossomos homólogos são ditos em ligação
ou denominados genes ligados.
Morgan e colaboradores foram os primeiros a demonstrarem que o
cromossomo X em Drosophila possuía vários genes. Em seus estudos, foi o
descobridor do fenômeno de ligação no cromossomo X, investigando numerosas
mutações de Drosophila, localizadas nesse cromossomo. Inicialmente, seus
cruzamentos levavam em consideração uma única característica, mas quando
começou a fazer cruzamentos experimentais, considerando duas características
ligadas ao cromossomo X, percebeu que os resultados obtidos em F 2 eram bem
diferentes daqueles obtidos, quando ocorria segregação independente, mas
também não era um resultado esperado para genes que estavam em um mesmo
cromossomo. Se os genes estavam localizados em um mesmo cromossomo,
deveriam ser transmitidos juntos e como consequência só seriam formados dois
tipos de gametas, os semelhantes aos parentais. (Cada par de homólogos tem um
cromossomo de origem materna e um de origem paterna, por isso, gametas que
contêm um desses cromossomos são ditos parentais).
Morgan estudou inicialmente as características: cor do corpo (amarelo e
cinza) e cor dos olhos (brancos e vermelhos), ao cruzar uma fêmea mutante de
olhos vermelhos e corpo amarelo, (XbaXba) com um macho selvagem, olhos
vermelhos e corpo cinza (XBAY), obteve em F 1 todo as fêmeas de olhos vermelhos e
corpo cinza (XBAXba) e todos os machos de olhos brancos e corpo cinza (XbaY). Ao
102
realizar o cruzamento das fêmeas F1 (XBAXba) com machos F1 (XbaY) a grande
maioria da prole em F2 mostrava o fenótipo parental, olhos vermelhos e corpo
cinza e olhos brancos e corpo amarelo, mas menos de 1% do total de moscas
nasceram com os olhos brancos e corpo cinza e olhos vermelhos e corpo amarelo
(tendo sido chamados de recombinantes por apresentarem uma mistura dos
fenótipos parentais). Depois desses resultados, Morgan e colaboradores realizaram
outros cruzamentos com genes ligados ao X, observando sempre o mesmo padrão
básico, ou seja, uma proporção fenotípica parental alta e uma proporção de
recombinantes baixa, mas sem um padrão definido com relação às proporções
fenotípicas (fig. 4.2).
103
Figura 4.2: Resultados de F1 e F2 do
cruzamento A que envolve as
mutações amarelo (a) e branco (b)
com o tipo selvagem , dados como
foram compilados por Sturtevant.
No cruzamento A, 0,5% das moscas
de F2 (machos e fêmeas)
demonstram fenótipos
recombinantes. Fonte: Klug et.al.,
2010.
104
As questões levantadas após esses resultados foram: O que leva a formação
dos recombinantes? E por que eles aparecem em cada cruzamento em uma
proporção diferente? Baseados em indícios citogenéticos, do pareamento dos
cromossomos homólogos na prófase I da meiose, observados por Janssens e
outros,
e
do
enrolamento
entre
esses
homólogos
e
surgimento
de
quiasmas(fig.4.3) interseções em forma de X, cujos pontos de sobreposição são
evidentes, Morgan propôs que esses quiasmas poderiam representar os pontos de
trocas genéticas (crossing-over). Logo, os recombinantes que surgem são
resultados dessa troca física “de pedaços” entre crom|tides homólogas.
Figura 4.3: Foto onde aparecem vários
quiasmas. Tiradas durante meiose em
testículos de gafanhotos. (John
Cabisco/Visuais Unlimited). Fonte:
Griffiths et. al.,2009
A segunda pergunta foi explicada por Morgan da seguinte forma: se dois
genes estão muito próximos um do outro, terão menos espaço físico entre eles para
permitir quebra e troca de pedaços (crossing-over), assim a possibilidade do
surgimento de recombinantes será menor, ou até não haverá recombinantes;
entretanto se os genes estão mais distantes terão mais espaço físico entre eles e
uma maior chance de que ocorra quebra e crossing-over ou permuta, originando
uma maior possibilidade de recombinantes. (fig.4.4)
105
Figura 4.4: Dois exemplos de uma
permutação única entre duas cromátides
não irmãs e dos gametas produzidos
subsequentemente. Em (a) a troca não
altera o arranjo de ligação entre os alelos
dos dois genes; formam-se somente
gametas parentais e a troca não é
detectada. Em (b) a troca separa os
alelos, resultando em gametas
recombinantes, que são detectáveis.
Fonte: Klug et. al., 2010.
Dessa forma Sturtevant, colaborador de Morgan, fez o primeiro mapa
genético, do cromossomo X, tomando como base a taxa de recombinação ou de
crossing-over entre os genes. A distância relativa entre os genes é dada pela taxa de
crossing-over ou permuta entre eles.
Outro exemplo de genes ligados estudados por Morgan foi o que afetava a
cor dos olhos (pr, púrpura, e pr+, vermelho) e o tamanho da asa (vg, vestigial, e
vg+, normal) em Drosophila. Como essas características são autossômicas, não foi
necessária a representação dos cromossomos sexuais. Os alelos selvagens pr+ e
vg+ são dominantes e Morgan realizou cruzamentos para obter di-híbridos e
cruzá-los com um duplo recessivo (cruzamento teste). O cruzamento teste é
importante, pois o genitor testador contribui com gametas levando apenas os
alelos recessivos, os fenótipos da prole revelam diretamente os alelos contribuídos
pelos gametas di-híbridos. Assim, a análise pode se concentrar na meiose em um
genitor (o di-híbrido) e, essencialmente esquecer a meiose no outro (o testador).
Em contraste, em um F1 autofecundado, existem dois conjuntos de meiose a
considerar na análise da prole: um no genitor masculino e um no feminino.
106
Os cruzamentos de Morgan estão representados a seguir: (existem várias
notações
usadas para representar os genes ligados algumas delas são aqui
apresentadas: pr+ vg+/ pr vg ou pr+ vg+//pr vg.)
P
pr vg/ pr vg
Gametas
pr vg
pr+ vg+/ pr+ vg+
pr+ vg+
pr+ vg+/ pr vg
Di-híbrido de F1
pr+ vg+/ pr vg
Cruzamento
X
X
pr vg/ pr vg
Teste
Gametas
pr vg
1ª
pr+ vg+
pr+ vg+/ pr vg
1339
2ª
pr vg
pr vg / pr vg
1195
3ª
pr+ vg
pr+ vg/ pr vg
151
4ª
pr vg+
pr vg+/ pr vg
154
2839
Obviamente, esses números desviam-se drasticamente da previsão
mendeliana de uma proporção 1:1:1:1. As duas primeiras combinações de alelos
est~o em grande maioria indicando claramente que est~o associadas ou “ligadas”. E
descendem dos gametas parentais. Os que aparecem em menor quantidade (3ª e
4ª combinações) são resultantes da quebra e troca de pedaços (crossing-over) e
são ditos recombinantes.
107
2. COMO CALCULAR A TAXA DE CROSSING-OVER OU PERMUTA
Considerando os dados do cruzamento teste acima, feito por Morgan,
podemos calcular a taxa de crossing-over entre os genes pr+ e vg+. O primeiro
passo é identificar quais os fenótipos que resultam de gametas recombinantes no
di-híbrido, no caso, os que aparecem em menor número. Nesse exemplo formaramse dois fenótipos recombinantes o que tem 151 descendentes (pr+ vg/ pr vg) e o
que tem 154 (pr vg+/ pr vg) descendentes no total de: 151 + 154 = 305
descendentes recombinantes. O segundo passo é calcular a frequência de
recombinação, que será o número total de recombinantes dividido pelo número
total de descendentes: 305 / 2839 ≈ 0,11. Multiplicando-se essa frequência por
100, teremos a taxa de crossing-over ou permuta igual a 11%.
As frequências de recombinantes para diferentes genes ligados variam de O
a 50%, dependendo de sua proximidade. Quanto mais distantes estão os genes,
mais proximamente suas frequências de recombinantes aproximam-se de 50%,e,
em tais casos, não podemos decidir se os genes estão ligados ou estão em
cromossomos diferentes.
Um único crossing gera dois produtos recombinantes recíprocos, o que
explica por que as classes recombinantes são, em geral, aproximadamente iguais
em frequência. E, por conseguinte, os parentais também devem ter iguais
frequências.
3. OS ARRANJOS “CIS” E “TRANS” DOS GENES LIGADOS
O trabalho de Morgan mostrou que os genes ligados em um di-híbrido
podem estar presentes em duas conformações básicas. Em uma, os dois alelos
dominantes ou selvagens se encontram em um cromossomo; e os dois alelos
recessivos ou mutantes, no outro. Esse arranjo é chamado conformação cis. Na
outra, eles estão em homólogos diferentes. Esse arranjo é chamado conformação
trans. (fig. 4.5)
108
Figura 4.5: Representação
esquemática de duas células uma em
conformação cis e outra em
conformação trans.
A identificação, se os dois genes ligados estão em posição cis ou trans, pode
ser feita analisando nos descendentes de um cruzamento teste (fig.4.6 a e b).
Cruzamento A B / a b
teste
X
ab/ab
Gametas masculinos
ab
AB
A B/a b
40%
Gametas
ab
a b/a b
40%
Femininos
Ab
A b/a b
10%
aB
a B/ab
10%
Parentais
Recombinantes
Figura 4.6a: Representação de um cruzamento teste, onde os parentais encontram-se
em conformação cis.
109
Cruzamento A b / a B
teste
X
ab/ab
Gametas masculinos
ab
Ab
A b/a b
40%
Gametas
aB
a B/a b
40%
Femininos
AB
A B/a b
10%
ab
a b/ab
10%
Parentais
Recombinantes
Figura 4.6b: Representação de um cruzamento teste, onde os parentais encontram-se
em conformação trans.
3. CONSTRUINDO MAPAS GENÉTICOS POR FREQUÊNCIA DE RECOMBINAÇÃO
3.1. TESTE DE DOIS PONTOS
Como já havíamos falado, quanto maior a distância física entre dois genes,
maior a possibilidade de quebra e troca de pedaços entre os cromossomos e,
consequentemente, maior a possibilidade de gametas recombinantes. Já quando
dois genes estão muito próximos, a taxa de recombinação entre eles é quase zero e
não teremos recombinantes.
A distância entre dois genes é diretamente
proporcional à taxa de recombinação ou crossing-over, logo, como a taxa de
crossing entre os genes pr+ e vg+ é igual a ≈ 11%, a dist}ncia entre os genes pr+ e
vg+ é igual a 11 UR( ou unidades de recombinação). Outra unidade usada para
expressar a distância entre dois genes é o centimorgan ou morganídeo e a
unidade de mapa genético u.m.. Cada u.m., UR ou cM ou morganídeo
corresponde a 1% da taxa de recombinação.
Esse método produz um mapa linear correspondente à linearidade
cromossômica?
110
Sturtevant previu que, em um mapa linear, se 5 UR. separam os genes A e ,
B, enquanto 3UR. separam A e C, então a distância que separa B e C deve ser de
8UR. ou 2UR.. Sturtevant viu que sua previsão era correta. Em outras palavras, sua
análise sugeriu fortemente que os genes estão dispostos em alguma ordem linear,
tornando as distâncias aditivas. A representação gráfica de um mapa é mostrada na
figura 4.7:
Figura 4.7: Uma região
cromossômica contendo três genes
ligados. Como as distâncias de
mapa são aditivas, o cálculo das
distâncias A—B e A-C nos deixa
com duas possibilidades
mostradas para a distância B-C.
Fonte: Griffiths et. al.,2009
Logo, para se poder construir o mapa gênico entre os genes A, B e C usando
o teste de dois pontos (determinação da distância usando um cruzamento teste
com um di-híbrido) seria necessário o conhecimento também da distância (= taxa
de recombinação entre os genes) entre os genes B e C. Caso a distância entre os
genes B e C fosse de 8UR a sequência dos genes seria CAB caso a freqüência entre B
e C fosse de 2UR teríamos a sequência de ACB.
111
3.2. TESTE DE TRÊS PONTOS
Quando o mapeamento é feito levando-se em conta as taxas de
recombinação em um cruzamento teste com um tri-híbrido, chamamos esse teste
de três pontos.
Vamos calcular a distância e a sequência de 3 genes usando como exemplo o
experimento feito por Bridges e Olbrycht., que cruzaram machos tipo selvagem de
Drosophila com fêmeas homozigotas para três mutações recessivas - cerdas scute
(sc), olhos echinus (ec) e asas crossveinless (cv). Em F1, nasceram fêmeas
heterozigotas para as três características, (elas herdaram um cromossomo X do
macho com as três características selvagem e um dos cromossomos X da fêmea
com as três características mutantes recessivas) e machos hemizigotos recessivos
(na herança ligada ao cromossomo X o macho só herda um cromossomo X, o da
fêmea, nesse caso, recessiva para as três características). Assim o entrecruzamento
entre machos e fêmeas F1 equivale a um cruzamento teste.
Entrecruzando fêmeas F 1 com machos F1 obtiveram em F2 oito tipos de
fenótipos diferentes, todos expressando os gametas produzidos pela fêmea, sendo
dois deles semelhantes aos fenótipos parentais e seis deles recombinantes. Os
parentais como sempre aparecem em uma proporção bem maior. Os
recombinantes em uma proporção bem menor, cada um representando um tipo
diferente de cromossomo com crossing. (fig.4.8)
Para entender quais crossings estavam envolvidos na produção de cada tipo
de recombinante, devemos primeiro determinar como os genes são ordenados no
cromossomo.
112
Figura 4.8: Cruzamento de três
pontos de Bridges e Olbrycht com os
genes ligados ao X sc (cerdas scute),
ec (olhos echinus) e cv (asas
crossveinless) em Drosophila. Fonte:
Snustad, D.Peter; Simmons, Michael
J.,2008.
3.2.1. DETERMINAÇÃO DA ORDEM DE GENES
Existem três possíveis ordens de genes:
1. sc—ec—cv
2. ec—sc—cv
3. ec—cv—sc
Outras possibilidades, tais como cv – ev – sc, são as mesmas que uma dessas, pois
as pontas esquerda e direita do cromossomo não podem ser distinguidas. Então,
como determinar a ordem?
A sequência dos procedimentos é o seguinte:
1º. definimos os recombinantes; que são seis, 4 com maior
freqüência e 2 com menor freqüência;
2º. definimos os que apresentam crossing duplo; no caso, os que
aparecem com menor frequência, já que é necessário que
113
ocorram dois crossing ao mesmo tempo, o que resulta
na
probabilidade de ocorrer o 1° e o 2º(P(1º) x P(2º));
3º. observamos nos duplos recombinantes, qual dos três genes
apresenta uma mudança em relação aos parentais; por exemplo:
os parentais são, nesse caso, sc ec cv e o outro sc+ ec+ cv+ , os
duplos recombinantes, sc ec+ cv e o outro sc+ ec cv+, o gene nos
recombinantes que mudou de lugar em relação aos parentais foi
o gene ec+, logo, o gene do meio é o ec+;
4º. a ordem correta do gene é sc ec cv.
3.2.2. Calculando a distância
Tendo estabelecido a ordem dos genes, podemos agora calcular as
distâncias entre os genes adjacentes (fig.4.10).
1st. Escolhemos dois genes adjacentes, sc e ec e identificamos as
classes recombinantes entre eles. (sc ec+ cv+), (sc+ ec cv), (sc ec+
cv) e (sc+ ec cv+).
2º. Somamos os números de descendentes de cada fenótipo
recombinante selecionado e dividimos pelo número total de
descendentes achando assim a frequência de recombinação
entre os dois genes(163+130+1+1=295)/ 3248=0,091).
3º. Achada a frequência, multiplicamos por 100 para achar a
distância entre os dois genes. (0,091x100= 9,1centiMorgan).
4º. O mesmo processo é repetido entre os genes ec e cv e achamos a
frequência de 0,105 que multiplicado por 100 dá uma distância
de 10,5 centiMorgan(cM).
A distância entre os dois genes extremos, sc cv , pode ser calculada
somando-se as distâncias entre cada um dos pares adjacentes: 9,1+10,5=19,6cM.
Dessa forma, o mapa pode ser assim representado (fig. 4.9):
114
Figura 4.9: Mapa de Bridges e
Olbrycht de sete genes ligados ao X
em Drosophila. As distâncias são
dadas em centiMorgans. Incluindo a
representação dos três genes
calculados no problema. Fonte:
Snustad, D.Peter; Simmons, Michael
J.,2008.
Também podemos obter esta estimativa calculando o número médio de
crossings entre estes genes:
Parentais: (1158+1455)= 2613/3248=0,805
Recombinantes com 1 só crossing:163+130+192+148= 633/3248=0,195 x
(1) = 0,195.
Recombinantes com 2 crossing: 1+1= 2/3248= 0,0006 x (2)= 0,0012.
Logo: parentais +recombinantes com 1 crossing + recombinantes com 2
crossing = 0,196
Figura 4.10: Cálculo das distâncias de mapa genético dos dados de Bridges e Olbrycht. A distância entre
cada par de genes é obtida estimando-se o número médio de crossings.Fonte: Snustad, D.Peter; Simmons,
Michael J.,2008.
115
3.2.3. INTERFERÊNCIA E COEFICIENTE DE COINCIDÊNCIA
Um teste de três pontos tem uma vantagem importante em relação a um
teste de dois pontos: ele permite a detecção de crossings duplos, permitindo-nos
determinar se as trocas em regiões adjacentes são independentes umas das outras.
Por exemplo, um crossing na região entre sc e ec ocorre independentemente de
um crossing na região entre ec e cv ? Ou um crossing inibe a ocorrência de outro
próximo?
Para responder a tais perguntas, devemos calcular a frequência esperada de
crossings duplos, com base na ideia de independência. Podemos fazer isso
multiplicando as frequências de crossing de duas regiões cromossômicas
adjacentes. Por exemplo, entre os genes sc e ec no mapa de Bridges e Olbrycht, a
frequência de crossing era (163 + 130 + 1 + 1)/3.248 = 0,091, e, entre ec e cv , ela
era (192 + 148 + 1 + 1)/3.248 = 0,105. Se for suposta independência (aplica-se a
regra do produto das probabilidades), a frequência esperada de crossings duplos
no intervalo entre sc e cv seria portanto de 0,09 1 x 0,105 = 0,0095. Podemos agora
comparar essa frequência com a frequência observada, que foi de 2/3.248 =
0,0006. Crossings duplos entre sc e cv foram muito menos frequentes do que o
esperado. Esse resultado sugere que um crossing inibiu a ocorrência de outro
próximo, um fenômeno chamado interferência. A intensidade da interferência
geralmente é medida pelo coeficiente de coincidência, c, que é a proporção entre a
frequência observada de crossings duplos e a frequência esperada:
c = Frequência observada de crossings duplos/ frequência esperada de
crossings duplos = 0,0006 / 0,0095 = 0,063
O nível de interferência, simbolizado por I, é calculado como
I = 1 - c = 1 – 0,063 = 0,937.
Como nesse exemplo o coeficiente de coincidência é próximo de zero, seu
menor valor possível, a interferência foi muito forte (I é próximo de 1). No outro
extremo, um coeficiente de coincidência igual a um significaria nenhuma
interferência; isto é, significaria que os crossings ocorreram independentemente
uns dos outros.
116
Muitos estudos mostraram que a interferência é forte em distâncias de mapa
menores que 20 cM; assim, crossings duplos raramente ocorrem em curtas regiões
cromossômicas. Entretanto, em regiões grandes, a interferência enfraquece a
ponto de crossings ocorrerem mais ou menos independentemente. A força da
interferência é, portanto, uma função da distância de mapa.
117