Apresentação Estatística Descritiva - Complexo HUPES

ESTATÍSTICA DESCRITIVA APLICADA NA
SAÚDE
Hospital Universitário Prof. Edgard Santos – UFBA
Unidade de Planejamento
Julho de 2016
AGENDA:





DEFINIÇÃO;
VARIÁVEIS (CONSTRUÇÃO DE UM BANCO DE DADOS);
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS;
BOXPLOT – OUTILIERS
SÍNTESE NÚMERICA PARA UMA VARIÁVEL QUANTITATIVA;
o
o
o
o
MEDIDAS DE TENDÊNCIA CENTRAL (MÉDIA E MEDIANA)
MEDIDAS DE VARIABILIDADE (DESVIO PADRÃO, COEFICIENTE DE VARIAÇÃO,
DESVIO INTERQUATÍLICO)
ASSIMETRIA E CURTOSE
MEDIDAS DE POSIÇÃO
ANÁLISE BIVARIADA;
TAXA, PROPORÇÃO E COEFICIENTE;
Hospital Universitário Prof. Edgard Santos – UFBA
Unidade de Planejamento
Julho de 2016
“Uma análise descritiva de dados bem-feita, representa “meio caminho
andado” no processo de análise dos dados e extração de conclusões de um
estudo”.
“O uso de técnicas descritivas deve sempre preceder análises mais avançadas.
Além de propiciar a familiarização com os dados, possibilita a detecção de
estruturas como, por exemplo, a distribuição dos dados ou o comportamento dos
dados e, eventualmente, valores atípicos ou mesmo incorretos”.
A estatística descritiva trata das ferramentas para: organizarmos e
descrevermos os dados, bem como , auxilia-nos na identificação de
valores típicos e na avaliação da variabilidade presente no dados.
Hospital Universitário Prof. Edgard Santos – UFBA
Unidade de Planejamento
Julho de 2016
VARIÁVEL.
Definição: Quantificação ou categorização de característica de interesse no estudo.
BANCO DE DADOS:
Após a coleta dos dados, o próximo passo é a construção do banco de dados.
Geralmente utilizamos planilha para a construção de banco de dados e via de regra, as
variáveis são colocadas nas colunas (campos) e os dados de cada indivíduo nas linhas
(observações ou registros)
Codificação das variáveis: ID (identificação da unidade respondente), EDU (Nível de
instrução. Variando de nenhuma (1) a curso superior (6)), PESO (Kg), ALT (altura em
cm), FUMO (Hábito tabagista. Não (0), Sim (1)), ATVFIS (Atividade física. Sedentário (1),
Alta (3)), GLIC (Glicose (md/dL)), COLEST (Colesterol total (mg/dL) e PSIST (Pressão
sistólica (mmHg)
Tipos de Variáveis
Qualitativas
Ordinal
Nominal
Quantitativas
Discretas
Contínuas
Intervalar
Razão
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
As tabelas e os gráficos são construídos a partir de determinado conjunto de dados,
proporcionando informações semelhantes ou complementares.
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS: TABELAS PARA DADOS CATEGÓRICOS.
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
DADOS QUANTITATIVOS CONTÍNUOS
1. Encontrar o mínimo e o máximo do conjunto de dados.
2. Calcular a amplitude total dos dados (máximo – mínimo)
3. Determinar o número de intervalos de classes.
 Algumas sugestões para determinarmos o número de classes

n
 Log2(n)
 1+3,32*log(n) (regra de Sturges)
4. Calcular a amplitude das classes (classes de igual amplitude)
5. Contar o número de elementos em cada classe.
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
Dados quantitativos: contínuos e discretos
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
Gráficos
1.
2.
3.
4.
5.
6.
Diagrama de barras (varáveis categóricas, ou quantitativas discretas)
Gráfico de setores
Histograma
Polígono de frequência
Ogiva.
Gráfico de linha (série temporal)
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
Gráficos
1. Diagrama de barras verticais ou horizontais (varáveis categóricas, ou quantitativas
discretas)
Figura 1: Diagrama de barras verticais construídos a partir dos dados de
frequência absoluta da variável atividade física dos elementos do
conjunto de dados.
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
Gráficos
1. Diagrama de barras horizontais ou horizontais (varáveis categóricas, ou
quantitativas discretas)
Figura 1: Diagrama de barras horizontais construídos a partir dos dados de
percentual sobre a escolaridade dos elementos do conjunto de dados
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
Gráficos
Gráfico de setores (varáveis categóricas, ou quantitativas discretas)
Figura 4: Gráfico de setores construído a partir dos dados da frequência
absoluta sobre o hábito de tabagismo dos elementos do conjunto de dados
ORGANIZAÇÃO E APRESENTAÇÃO DOS DADOS.
Gráficos
Histograma
Figura 3: Diagrama de barras horizontais construídos a partir dos dados de
percentual sobre a escolaridade dos elementos do conjunto de dados
HISTOGRAMA, POLÍGONO DE FREQUÊNCIA, OGIVA
HISTOGRAMA, POLÍGONO DE FREQUÊNCIA, OGIVA
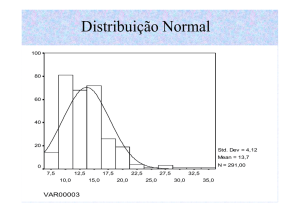
Figura 5: Histograma, polígono de frequência e ogiva para as frequências simples e relativa
acumulada para os dados da tabela de frequências da variável ácido úrico
Os gráficos acima mostram que a distribuição da dosagem de ácido úrico em indivíduos normais de
sexo masculino é razoavelmente simétrica. A variação desta dosagem está entre 3,0 e 9,0 mg/dL, com
maior concentração em torno de 5,0 a 5,5 mg/dL (20,2%). Além disto , 96,6% dos homens dessa
amostra apresentaram valores de ácido úrico sérico de 3,5 a 7,5 mg/dL.
REPRESENTAÇÃO GRÁFICA DE DADOS TEMPORAIS:
Dados coletados ao longo do tempo são muito comuns em pesquisas médicas e
em registros de saúde pública. Tais dados são denominados temporais ou
longitudinais, ou ainda, de medidas repetidas. O gráfico de linhas é a representação
mais apropriada para este tipo de dados.
Figura 6: Tempo médio de permanência por leito clínico e leito cirúrgico no HUPES. No período
de novembro/13 a junho/15
IDENTIFICAÇÃO DE OUTILIERS E BOXPLOT:
Figura 7: Boxplot – Pressão sistólica estratificada por hábito tabagista. Não possui (0) e Possui
(1)
IDENTIFICAÇÃO DE OUTILIERS E BOXPLOT:
Podem-se distinguir dois tipos de outliers: 1;
outlier não genuíno, considerado erro , outlier
genuíno que pode refletir uma característica do
que está sendo estudado.
Observações atípicas alteram significativamente
a médias e a variabilidade do grupo a que
pertencem e podem distorcer as conclusões
obtidas a partir da análise estatística.
Causas para o surgimento dos outliers:
 Erro na coleta do dado;
 Erro na execução do experimento (medida);
 Mudanças não controláveis na condição do
experimento (ou do indivíduo);
 Característica inerente à variável estudada.
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MÉDIA.
n

x x

x

1
...
2
n
xn 
x
i
i 1
n
MEDIANA: Uma medida de tendência central adequada para distribuições
assimétricas. Por definição, a mediana é o valor que divide a distribuição ao meio.
Para o cálculo da mediana , é necessário primeiramente ordenar a amostra para
localizar a posição da mediana e, assim, encontrar seu valor. Se n for ímpar a
posição da mediana é dada por (n+1)/2. Se n é par, não existe uma posição central.
Portanto convencionou-se usar a média aritmética desses dos valor na posição n/2
e (n+2)/2
12345
123456
57788
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE VARIABILIDADE - VARIÂNCIA.
A variância é uma medida da variabilidade dos dados em torno da média. É
natural procurar uma medida de dispersão que dependa dos desvios de cada


observação em relação à média  x  x  e seria razoável considerar a soma destes
desvios. E quanto maior a soma destes desvios , maior seria a variabilidade
presente neste conjunto de dados. Entretanto pela definição da média   x  x   0

i
n
i 1


i

para qualquer conjunto de dados . Uma alternativa é elevar os desvios ao
quadrado. Torna-se levar em consideração o número de observações, pois o
acréscimo de observações aumenta o valor do somatório, portanto dividiríamos o
somatórios dos desvios em relação à media ao quadrado por n a quantidade de
dados. Contudo a definição mais conhecida para a variância amostral é:
n
s
2


i 1



 xi  x 


n 1
2
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE VARIABILIDADE – DESVIO PADRÃO
Registra-se que a variância tem a unidade de medida das observações elevada
ao quadrado. Por exemplo, se as observações foram medidas em ºC , a unidade da
variância será ºC^2. Logo para obter uma medida de variabilidade com a mesma
unidade das observações, extrai-se a raiz quadrada. Com isso temos o desvio
padrão:
n

s
i 1



 xi  x 


n 1
2
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE VARIABILIDADE – COEFICIENTE DE VARIAÇÃO
Uma pergunta que surge é se um desvio padrão é elevado ou reduzido. Isso é
relativo. Por exemplo, um desvio padrão de 10 pode ser pequeno se a observação
típica for 1000, mas poderá ser considerado bastante elevado para um conjunto de
dados cuja observação típica seja 20.
Portanto, em alguns casos é conveniente exprimir a dispersão em termos
relativos, ou seja tirando a influência da ordem de grandeza da variável. Pode-se
obter índice relativo de dispersão comparando-se o desvio padrão (s) com a média

A medida utilizada é denominada coeficiente de variação e é definida por:
x
CV 
s

x
O coeficiente de variação é muito útil na comparação de duas variáveis ou
dois grupos que a princípio não são comparáveis, por exemplo com ordem de
grandeza diferentes ou com características diferentes, como crianças e
adultos
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE FORMATO - ASSIMETRIA E CURTOSE
Uma distribuição é dita simétrica quando as medidas de tendência central
(média, media e moda) são coincidentes.
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE FORMATO - ASSIMETRIA E CURTOSE
Dá-se o nome de curtose ao grau de achatamento da distribuição.
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE FORMATO - ASSIMETRIA E CURTOSE
= 0,263 mesocúrtica
> 0,263 leptócurtica
< 0,263 platicúrtica
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE VARIABILIDADE – ESCORE PADRONIZADO (z).
O escore padronizado, ou escore z, aborda o relacionamento entre a média e o
desvio padrão, mas para cada indivíduo. Esta medida é muito utilizada pelos
pediatras para acompanhar o desenvolvimento da criança em relação à população.

Sejam x1,...,xn os dados observados em uma amostra de tamanho n, x , s a
média é o desvio padrão, respectivamente. Quando s > 0, define-se o escore
padronizado da observação xi, como o desvio da i-ésima observação em relação à
media dividida pelo desvio padrão, isto é:

z
x
x

, i  1,..., n
i
i
s
SÍNTESE NUMÉRICA PARA UMA VARIÁVEL
MEDIDAS DE POSIÇÃO – PERCENTIS
Dados provenientes de distribuições simétricas são adequadamente descritos e
sintetizados pela média e pelo desvio padrão.
Isto não ocorre quando os dados são assimétricos. Como já comentamos a
mediana identifica mais adequadamente o “centro” de um conjunto de dados com
distribuição assimétrica. Para entender bem uma distribuição, é preciso conhecer
valores acima ou abaixo dos quais se encontra determinada porcentagem dos
dados – essas medidas são chamadas de percentis. Em outras palavras, o percentil
é o valor que acumula determinado percentual. Os percentis de ordem 25, 50 e 75
são chamados respectivamente, de primeiro, segundo e terceiro quartis, por que
divide o conjunto de dados em quatro partes iguais.
Para determinar a posição dos quartis EQi =( i*n)/4
ANÁLISE BIVARIADA
É muito comum e extremamente o estudo sobre a relação entre variáveis.
Podem-se citar os seguintes exemplos:
i. Volume de expiração forçada no primeiro segundo (Y) em função da altura (X);
ii. Estudo sobre a influência do índice de massa corpórea (X), na pressão sistólica
(Y).
SÍNTESE NUMÉRICA PARA DUAS VARIÁVEIS
DIAGRAMA DE DISPERSÃO
O objetivo do estudo de correlação é descobrir se há relação entre duas
variáveis. Para o estudo de correlação entre duas variáveis quantitativas (X e Y) ps
dados de uma amostra de tamanho n é: (x1, y1), (x2, y2),...,(xn, yn). A variação
conjunta de duas variáveis pode ser visualizada a partir do diagrama de dispersão
SÍNTESE NUMÉRICA PARA DUAS VARIÁVEIS
COEFICIENTE DE CORRELAÇÃO DE PEARSON
Os gráficos acima ilustram apenas a avaliação gráfica da presença ou não de correlação
linear entre duas variáveis, entretanto está análise gráfica não é suficiente. Com isso torna-se
necessária a quantificação do grau de correlação entre as variáveis:
O coeficiente de correlação de Pearson expressa numericamente tanto a força
quanto o sentido da relação e apresenta as seguintes propriedades:
• É uma quantidade adimensional.
• Varia entre -1 e 1
• É invariante em relação a escala linear
• Se 0 < |r| <0,4 a correlação é dita fraca
• Se 0,4 ≤ |r| < 0,7 a correlação é dita moderada
• Se 0,7 ≤ |r| < 1,0 a correlação é dita forte.
COMPARAÇÃO ENTRE PROPORÇÃO, RAZÃO E TAXA
Do ponto de vista estatístico, representam medidas simples, mas que permitem
estabelecer comparações entre grupos.
Proporção: A proporção de indivíduos em uma dada categoria é definida através
do quociente entre o número de indivíduos desta categoria e o número total de
indivíduos considerados.
Razão (A/B): O termo razão é utilizado quando A e B representam características
separadas e distintas: Ex médico/habitante.
Taxa: É uma estimativa de “risco” da ocorrência de determinado fenômeno. É
usual a multiplicação por um fator múltiplo de 10 .
Ex: Taxa de natalidade, Taxa de mortalidade.
OBRIGADO!
BIBLIOGRAFIA



ESTATÍSTICA NA ÁREA DA SAÚDE: CONCEITOS, METODOLOGIA, APLICAÇÕES E PRÁTICA COMPUTACIONAL – Arminda Lúcia
Siqueira e Jaqueline Domingues Tibúrcio
Notas de aula MAT 027 – Estatística IV – Departamento de Estatística – Universidade Federal da Bahia .
Estatística Básica – Wilton Bussab e Pedro A Morettin