ESCOLA SECUNDÁRIA ANTÓNIO NOBRE

y
Electroíman
1
2
h1
h2
Colisão
P
O
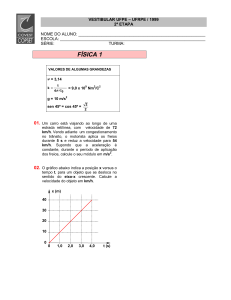
Sobre uma rampa é lançada uma bola 1 que a abandona horizontalmente. À mesma altura, uma outra bola
2 cai verticalmente, a partir do repouso. O dispositivo tem um mecanismo que permite que a bola 2 seja
libertada no instante em que a bola 1 deixa a rampa horizontalmente. As duas bolas caem da mesma
altura, h1 = h2 = 1,2 m, e percorrem a mesma distância vertical no mesmo intervalo de tempo, o que é
confirmado pelo facto de colidirem uma com a outra no ar, na posição assinalada pelo ponto P.
1. De acordo com o enunciado, um corpo em queda livre cai 5 metros no primeiro segundo. Será que o
mesmo acontece no segundo seguinte? Fundamente a sua resposta. (8 pontos)
2. Para a bola 2 em queda livre, calcule o valor da sua aceleração a partir da lei da gravitação universal
e compare-o com o valor apresentado no formulário, sabendo que o raio da Terra é de 6,37×106 m. (8
pontos)
3. Em relação ao referencial xOy representado na figura, a posição assinalada pelo ponto P tem
coordenadas cartesianas (4,0 ; 0,8) m.
Calcule, explicitando o seu raciocínio:
3.1.
O intervalo de tempo que decorreu desde que cada bola iniciou a queda até que colidiram
uma com a outra. (10 pontos)
3.2.
O módulo da velocidade com que a bola 1 abandona horizontalmente a rampa. (8 pontos)
4. Calcule o módulo da velocidade das duas bolas no instante imediatamente antes da colisão. (12
pontos)
5. Posteriormente, foi retirada a bola 2, mas a bola 1 abandona a rampa nas mesmas condições. A que
distância da vertical de lançamento é que a bola 1 atinge o solo? Apresente todos os cálculos. (12
pontos)
GRUPO II
A força produzida pelos motores de uma nave espacial faz com que haja variação da sua
velocidade, ou seja que ela acelere. Existe uma relação entre a resultante das forças que
actua sobre um corpo e a aceleração que ele adquire.

Um corpo de massa 2,0 kg, desloca-se sobre um plano horizontal, quando sobre ele actua uma força F ,
que faz um ângulo 30º com a horizontal, de módulo 14 N. Do contacto da caixa com a superfície
horizontal resulta uma força de atrito.
Considere as duas situações:
I- O corpo desloca-se sobre uma superfície com velocidade constante.
II- O corpo tem movimento sobre uma superfície com aceleração constante de módulo 1,0 m.s -2.
1. Represente num esquema todas as forças que estão aplicadas no corpo, tendo em conta o
comprimento dos vectores. (8 pontos)

2. Calcule os valores das componentes horizontais e verticais da força F . (8 pontos)
3. Para cada uma das situações referidas, calcule:
3.1.
O módulo da força de atrito entre o corpo e a superfície. (12 pontos)
3.2.
O módulo da reacção normal da superfície sobre o corpo. (12 pontos)
4. Escreva um pequeno texto comparando a situação I com a de uma nave espacial fora da atracção
gravitacional da Terra, ou de outro planeta. Tenha em atenção que em qualquer dos casos se aplica
uma lei importante. (12 pontos)
GRUPO III
Para que um satélite seja colocado em órbita, é necessário lançá-lo conjuntamente com uma
foguetão, a partir de uma posição conveniente situada à superfície da Terra. No lançamento
de um satélite, provoca-se a conversão da energia química em energia potencial gravítica e em
energia cinética. O foguetão utilizado no lançamento deve abandonar o satélite no espaço com
energia suficiente de modo a que este possa descrever um trajectória circular com centro no
centro da Terra, isto é tal que a força gravitacional tenha uma direcção que, em cada
instante, seja perpendicular à da velocidade.
Considere que o raio da Terra é de 6,37×106 m.
1. Calcule o valor da velocidade angular da Terra em torno do seu eixo. (8 pontos)
2. Indique o valor lógico das seguintes proposições (V ou F). (12 pontos)
(A)
(B)
(C)
(D)
(E)
(F)
Quando um veículo contorna uma rotunda, deve manter a sua velocidade.
Um corpo descreve um movimento rectilíneo quando a aceleração tangencial é nula.
Se um objecto for lançado de uma altura 2 vezes maior, atingirá o solo com o dobro da
velocidade.
Satélites de massa diferentes colocados à mesma distância da Terra giram com
velocidade orbitais iguais.
Um corpo segue uma trajectória rectilínea. Se quisermos torná-la curvilínea, teremos de
lhe aplicar uma força numa direcção diferente da direcção da trajectória inicial.
Um satélite geostacionário orbita com velocidade constante.
3. Um satélite artificial descreve uma trajectória aproximadamente circular a 70000 km da superfície
da Terra, com um período de 10000 minutos.
3.1. Calcule a velocidade angular do satélite. (9 pontos)
3.2. Calcule a velocidade linear do satélite. (8 pontos)
3.3. Por vezes, é necessário reduzir o valor da velocidade do satélite. Qual dos seguintes esquemas
corresponde à aceleração do satélite durante a “travagem”: (8 pontos)



v
(A)

a

v

a
(B)

v

a
(C)

v
a
(D)

v
a
(E)
Grupo IV
Um sinal é uma perturbação, de qualquer espécie, que é usada para comunicar, ou transmitir, uma
mensagem e que formalmente, é uma função que veicula informação acerca de determinado fenómeno
físico.
Quando se provoca deformação num meio elástico, por exemplo numa região da superfície livre da água
em repouso, põe-se em jogo certa quantidade de energia mecânica que é transportada pela onda.
1. Considere as ondas que resultam da propagação de uma perturbação nas seguintes situações:
A. Campainha a tocar; B. abalo sísmico; C. Lâmpada acesa; D. compressão de algumas espiras de
uma mola em hélice, que depois se abandonam; E. Pedra que cai na superfície de água em repouso.
Classifique, justificando, as ondas que resultam destas perturbações. (14 pontos)
2. Considere o seguinte gráfico que representa a elongação y da extremidade de uma corda muito
comprida animada de movimento harmónico simples.
2.1. Calcule o número de oscilações que a extremidade da
corda executa por segundo. A que grandeza corresponde
esse número? (8 pontos)
2.2. Escreva, no SI, a equação que descreve a função y=f(t)
da extremidade da corda. (8 pontos)
2.3. A velocidade de propagação da onda ao longo da corda,
a que se refere o gráfico tem módulo 10 m/s. Indique o
valor lógico das seguintes proposições (V ou F): (6 pontos)
(A)
A distância entre duas cristas sucessivas é 60 cm.
(B)
A onda percorre 24 m em 2,0 segundos.
(C)
O período das oscilações para outros pontos da corda é igual ao período de oscilação da
extremidade da corda.
(D)
A extremidade da corda afasta-se no máximo 30 cm da posição de equilíbrio.
(E)
O valor da frequência de vibração da extremidade da corda é 0,53 Hz.
(F)
Um satélite geostacionário orbita com velocidade constante.
3. Comente. a seguinte afirmação: “Não é cientificamente correcto pedir a alguém para falar mais alto
quando a sua voz não se faz ouvir”. (9 pontos)