História da Trigonometria

Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Prática de Ensino III – Quest_V
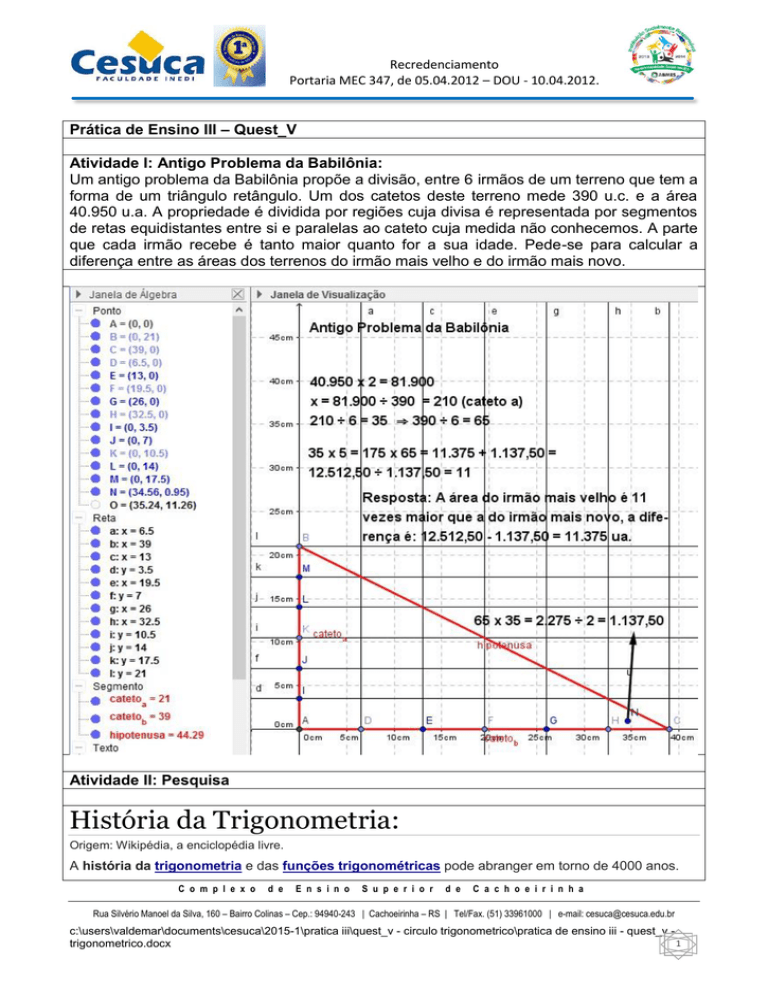
Atividade I: Antigo Problema da Babilônia:
Um antigo problema da Babilônia propõe a divisão, entre 6 irmãos de um terreno que tem a
forma de um triângulo retângulo. Um dos catetos deste terreno mede 390 u.c. e a área
40.950 u.a. A propriedade é dividida por regiões cuja divisa é representada por segmentos
de retas equidistantes entre si e paralelas ao cateto cuja medida não conhecemos. A parte
que cada irmão recebe é tanto maior quanto for a sua idade. Pede-se para calcular a
diferença entre as áreas dos terrenos do irmão mais velho e do irmão mais novo.
Atividade II: Pesquisa
História da Trigonometria:
Origem: Wikipédia, a enciclopédia livre.
A história da trigonometria e das funções trigonométricas pode abranger em torno de 4000 anos.
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 1
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Desenvolvimento:
A trigonometria não é obra de um só homem ou nação. A sua história tem milhares de anos e faz parte
de todas as grandes civilizações. Deve ser notado que, desde os tempos de Hiparco até os tempos
modernos, não havia tal coisa como "razão" trigonométrica. Ao invés disso, os gregos e depois os
hindus e os muçulmanos usaramlinhas trigonométricas. Essas linhas primeiro tomaram a forma
de cordas e mais tarde meias cordas, ou senos. Essas cordas e linhas de senos então seriam
associadas a valores numéricos, possivelmente aproximações e listados em tabelas trigonométricas.2
Trigonometria antiga:
Os antigos egípcios e babilônicos conheciam teoremas sobre as razões dos lados de triângulos
semelhantes por muitos anos. As sociedades pré-helênicas não possuíam o conceito de medida de um
ângulo e, consequentemente, eram estudados os lados do triângulo, um campo de estudo que seria
melhor chamado de "trilaterometria".3
Com base na interpretação da tábua cuneiforme Plimpton 322 (cerca de 1900 a.C.), tem-se afirmado
que os babilônicos antigos tinham uma tábua de secantes.4 No entanto, existe muito debate sobre se
ela é uma tabela de trinas pitagóricas, soluções de equações quadráticas ou uma tábua trigonométrica.
Matemática grega:
A corda de um ângulo subentende o arco do ângulo.
Os matemáticos helênicos fizeram uso da corda. Dados um círculo e um
arco nesse círculo, a corda é a linha que subentende o arco. Uma bissetriz
perpendicular da corda passa através do centro do círculo e bissecciona o
ângulo. Uma metade da corda bisseccionada é o seno do ângulo
bisseccionado, isto é,
, e consequentemente a função
seno é também conhecida como "meia corda". Devido a essa relação,
muitas das identidades trigonométricas e teoremas conhecidos hoje
também o eram aos matemáticoshelênicoss, mas na sua forma equivalente
de corda.5
Apesar de que não há nenhuma trigonometria nos trabalhos de Euclides e de Arquimedes, estritamente
falando, existem teoremas apresentados de uma forma geométrica que são equivalentes a fórmulas ou
leis trigonométricas específicas.3 Por exemplo, as proposições 12 e 13 dos Elementos são a lei dos
cossenos para ângulos agudos e obtusos, respectivamente. Teoremas a respeito do comprimento das
cordas são aplicações da lei dos senos. E o teorema de Arquimedes sobre cordas rompidas é
equivalente às fórmulas para o seno de somas e diferenças de ângulos.3 Para compensar a falta de
uma tabela de cordas, os matemáticos da época de Aristarco de Samos às vezes usavam um
conhecido teorema de que, na notação moderna, sin α/ sin β <α/β < tan α/ tan β sempre que 0° < β < α
< 90°, dentre outros.6
A primeira tabela trigonométrica foi aparentemente compilada por Hiparco de Niceia (180–125 a.C.),
que é agora conhecido como o "pai da trigonometria."7 Hipparchus was the first to tabulate the
corresponding values of arc and chord for a series of angles.1 7
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 2
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Uma representação medieval de Cláudio Ptolomeu
Apesar de não se saber quando o uso sistemático do círculo de 360°
passou a fazer parte da matemática, é sabido que sua introdução se deu
um pouco depois de Aristarco de Samos ter escrito Sobre os Tamanhos e
Distâncias do Sol e da Lua (ca. 260 a.C.), uma vez que ele mede o
ângulo em termos da fração de um quadrante.6 Parece que o uso
sistemático do círculo de 360° é em boa medida devido a Hiparco e sua
tabela de cordas. Hiparco pode ter tirado a idéia dessa divisão
de Hípsicles, que tinha anteriormente dividido o dia em 360 partes, uma
divisão do dia que deve ter sido sugerida pela astronomia babilônica.8 Na
astronomia antiga, o zodíaco havia sido dividido em doze "signos" ou 36
"decanos". Um ciclo sazonal de aproximadamente 360 dias pode ter
correspondido aos signos e decanos do zodíaco, dividindo cada signo em
trinta partes e cada decano em dez partes.2 It is due to the Babylonian
sexagesimal number system that each degree is divided into sixty minutes
and each minute is divided into sixty seconds.2
Menelau de Alexandria (ca. 100 a.C.) escreveu em três livros chamados Sphaerica. No Livro I, ele
estabelece uma base para triângulos esféricos análogos à base de Euclides para os triângulos
planos.5 Ele estabeleceu um teorema sem análogo em Euclides, que dois triângulos esféricos são
congruentes se os ângulos correnpondentes são iguais; no entanto, ele não estabeleceu uma distinção
entre triângulos esféricos simétricos e congruentes.5 Outro teorema estabelecido por ele é que a soma
dos ângulos de um triângulo esférico é maior do que 180°.5 O Livro II de Sphaerica aplica a geometria
esférica à astronomia e o Livro III contém o "teorema de Menelau".5 Ele ainda deu a sua famosa "regra
das seis quantidades".9
Mais tarde, Cláudio Ptolomeu (ca. 90 - ca. 168) expandiu as Cordas em um Círculo de Hiparco no
seu Almagesto, ou a Sintaxe Matemática. Os treze livros doAlmagesto são os mais influentes e
significativos trabalhos sobre trigonometria de toda a antiguidade.10 Um teorema central para o cálculo
das cordas de Ptolomeu é conhecido ainda hoje como teorema de Ptolomeu e diz que a soma dos
produtos dos lados opostos de um quadrilátero cíclico é igual ao produto das diagonais. Um caso
especial do teorema de Ptolomeu apareceu como a proposição 93 na obra Data, de Euclides. O
teorema de Ptolomeu leva ao equivalente das quatro fórmulas de soma e diferença para senos e
cossenos, conhecidas como fórmulas de Ptolomeu, apesar de que Ptolomeu na verdade usava cordas
em vez de seno e cosseno. Ptolomeu ainda derivou o equivalente à fórmula da metade de um
ângulo
. Ele usou esses resultados para criar suas tabelas
trigonométricas, mas não é possível ser determinado se elas foram derivadas do trabalho de Hiparco.10
Nem as tabelas de Hiparco nem as de Ptolomeu sobreviveram aos nossos dias, mas descrições delas
feitas por outros autores antigos deixam pouca dúvida da sua existência.11
Matemática hindu:
Estátua de Ariabata
O próximo desenvolvimento da trigonometria foi realizado na Índia.
O matemático-astrônomo Ariabata (476–550), na sua obra Ariabata-Sidanta,
primeiro definiu o seno como a relação moderna entre a metade de um ângulo e
a metade de uma corda e então definiu o cosseno, verseno e o seno inverso.
Seus trabalhos também contém as tabelas de valores de seno e verseno
(1 − cosseno) mais antigas que sobreviveram até nós, em intervalos de 3.75° de
0° até 90°, com uma precisão de 4 casas decimais. Ele usou as palavras jya para
seno, kojya para cosseno, ukramajya para verseno e otkram jya para seno
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 3
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
inverso. As palavras jya e kojya eventualmente se transformaram em seno e cosseno, respectivamente,
depois de traduções equivocadas.
Outros matemáticos hindus expandiram os trabalhos de Ariabata sobre trigonometria. No século
VI, Varahamihira usou as fórmulas:
No século VII, Bhaskara I produziu uma fórmula para calcular o seno de um ângulo agudo sem o uso de
tabelas. Ele também forneceu uma fórmula de aproximação para sin(x) com uma margem de
erro relativa de menos de 1.9%:
Mais
tarde
no século
VII, Brahmagupta desenvolveu
fórmula
Brahmaguptapara computar valores de seno.
a
assim como a fórmula de interpolação de
Matemática islâmica:
al-Khawarizmirepresentado num selo comemorativo soviético
Os trabalhos dos matemáticos hindus foram mais tarde traduzidos e
expandidos
no mundo
islâmico por matemáticos árabes e persas.
No século IX, al-Khwārizmī produziu tabelas precisas de senos e
cossenos e a primeira tabela de tangentes. Ele também foi uma pioneiro
na trigonometria esférica.
Pelo século X, na obra de Abū al-Wafā' al-Būzjānī, matemáticos islâmicos
estavam usando todas as seis funções trigonométricas, depois de
descobrir as funções secante, cotangente e cossecante. Abu al-Wafa
tinha tabelas em intervalos de 0.25°, com precisão de 8 casas decimais e
tabelas bastante precisas de valores de tangentes. Ele também
desenvolveu a seguinte fórmula trigonométrica:
Também no século X, Al-Battani foi responsável por estabelecer um número importante de relações
trigonométricas, como:
Al-Jayyani (989–1079) de al-Andalus escreveu um tratado sobre trigonometria esférica
chamado O livros dos arcos desconhecidos de uma esfera, que "contém fórmulas
para triângulos retângulos especiais, a lei dos senos geral e a solução de um triângulo
esférico zatravés de um triângulo polar." Mais tarde esse tratado exerceu uma "forte influência
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 4
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
sobre a matemática européia", e sua "definição de razões como números" e "método para
resolver um triângulo esférico quando todos os lados são conhecidos" provavelmente
influenciaram Regiomontanus.12
No século XI, Omar Khayyām (1048–1131) resolveu equações cúbicas usando
numéricas aproximadas encontradas por interpolações em tabelas trigonométricas.
soluções
Outros autores de assuntos trigonométricos incluem Bhaskara II e Nasir al-Din al-Tusi no século
XIII. Nasir al-Din al-Tusi enunciou a lei dos senos fornecendo uma prova e também listou seis
casos distintos para triângulos retângulos na trigonometria esférica.
No século XIV, Ghiyath al-Kashi forneceu tabelas trigonométricas de valores para a função seno
para quatro dígitos sexagesimais (o equivalente a 8 casas decimais) para cada 1° de
argumento com diferenças adicionáveis para cada 1/60 de 1°. Ulugh Beg (século XIV) também
forneceu tabelas precisas de senos e tangentes com precisão de 8 casas decimais.
O método da triangulação foi primeiramente desenvolvido por matemáticos muçulmanos que o
deram aplicações práticas como na cartografia.13
China:
Guo Shoujing (1231–1316)
Na China, a tábua de senos de Ariabata foi traduzida para o
chinês no livro de matemática de Kaiyuan Zhanjing, compilado
em 718durante a Dinastia Tang.14 Apesar de os chineses terem
realizado grandes avanços em outros campos da matemática
como a geometria sólida, teorema binomial, e complexas
fórmulas algébricas, as formas antigas de trigonometria não eram
tão apreciadas como na Grécia antiga ou depois na Índia ou no
mundo Islâmico.15 Ao invés delas, os chineses usavam um
substituto empírico conhecido como chong cha, apesar de que o
uso prático da trigonometria plana usando o seno, a tangente e a
secante já fosse conhecido.14 Apesar de tudo isso, esse estado
embriônico da trigonometria na China começou a mudar
lentamente durante a Dinastia Song (960–1279), em que
matemáticos chineses começaram a expressar maior ênfase na necessidade da trigonometria
esférica nos cálculos astronômicos e para os calendários.14 O polímata, cientista, matemático e
oficial chinês Shen Kuo (1031–1095) usou funções trigonométricas para resolver problemas
matemáticos de cordas e arcos.14 Victor J. Katz escreve que, na fórmula de Shen, "técnica de
intersecção de círculos", ele criou uma aproximação do arco de um círculo s dado o diâmetro d,
sagita v, e comprimento de corda csubentendendo o arco, cujo comprimento ele aproximou
como sendo s = c + 2v²/d.16 Sal Restivo escreve que o trabalho de Shen sobre os comprimentos
de arcos de círculo forneceu a base para a trigonometria esférica desenvolvida no século
XIII pelo matemático e astrônomo Guo Shoujing (1231–1316).17 De acordo com os historiadores
L. Gauchet e Joseph Needham, Guo Shoujing usou a trigonometria esférica nos seus cálculos
para melhorar o sistema de calendário e a astronomia chinesa.14 18 Junto de uma ilustração
do século XVII das provas matemáticas de Guo, Needham diz:
Guo usou uma pirâmide quadrangular esférica, cujo quadrilátero de base consistia em
um arco equatorial e outro elíptico, juntos com dois arcos meridianos,um dos quais
passava pelo ponto do solstício de verão… Através desses métodos ele foi capaz de
obter os du lü (graus de equador correspondentes aos graus da eclíptica), os ji
cha (valores das cordas para dados arcos elípticos) e os cha lü (diferença entre cordas
de arcos com diferença de 1 grau).19
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 5
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Apesar das descobertas de Shen e Guo na trigonometria, outro trabalho substancial sobre o
tema não seria publicado até 1607, com a dupla publicação de Os Elementos de Euclides pelo
oficial e astrônomo chinês Xu Guangqi (1562–1633) e pelo jesuíta italiano Matteo Ricci (1552–
1610).20
Europa renascentista:
Isaac Newton em um retrato deGodfrey Kneller de 1702.
Regiomontanus foi talvez o primeiro matemático na Europa a
tratar a trigonometria como uma disciplina matemática
distinta,21 no seu De triangulis omnimodus escrito em 1464,
assim como no posterior Tabulae directionum, que incluía a
função tangente, mas sem nome.
A Opus palatinum de triangulis de Georg Joachim Rheticus,
um aluno de Nicolau Copérnico, foi provavelmente o primeiro
a definir as funções trigonométricas diretamente em termos
de triângulos retângulos ao invés de círculos, com tabelas
para todas as seis funções trigonométricas. Esse trabalho foi
terminado pelo aluno de Rheticus, Valentin Otho, em 1596.
No século XVII, Isaac Newton e James Stirling desenvolveram a fórmula de interpolação geral
Newton-Stirling para funções trigonométricas.
Análise trigonométrica:
Madhava de Sangamagrama (c. 1400) deu contribuições à análise das funções trigonométricas
e das suas expansões em séries infinitas. Ele desenvolveu os conceitos de série de potências e
de série de Taylor, e produziu as expansões em séries trigonométricas do seno, cosseno,
tangente e arcotangente. Usando as aproximações de Taylor de seno e cosseno ele produziu
uma tabela de senos com 12 casas decimais de precisão e uma tabela de cossenos com 9
casas
decimais
de
precisão.
Ele
também
forneceu
séries
de
potência
para πe θ, raio, diâmetro e circunferência de um círculo em termos de funções trigonométricas.
Seu trabalho foi expandido pelos seus seguidores na Escola de Kerala até oséculo XVI.22 23
A Introductio in analysin infinitorum (1748) de Leonhard Euler foi o principal responsável por
estabelecer o tratamento analítico dado às funções trigonométricas na Europa, definindo-as
como séries infinitas e apresentando a "Fórmula de Euler" eix = cos(x) + i sin(x). Euler usou as
quase-modernas abreviações sen., cos., tan., cot.,sec. e cosec.
Brook Taylor definiu a série geral de Taylor e deu as expansões e aproximações para todas as
seis funções trigonométricas. Os trabalhos de James Gregory e Colin Maclaurin também foram
muito influentes no desenvolvimento das séries trigonométricas.
Ver também:




Matemática grega
História da matemática
Função trigonométrica
Trigonometria
Fonte: https://pt.wikipedia.org/wiki/Hist%C3%B3ria_da_trigonometria
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 6
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Triângulo retângulo
Origem: Wikipédia, a enciclopédia livre.
ΔABC é um triângulo retângulo, pois BĈA = 90°
Triângulo retângulo, em geometria, é um triângulo que possui um ângulo reto e outros dois ângulos
agudos, para tanto basta que tenha um ângulo reto (90°), pois a soma dos três ângulos internos é igual
a um ângulo raso (180°). É uma figura geométrica muito usada na matemática, no cálculo de áreas,
volumes e no cálculo algébrico. Em um triângulo retângulo, sabendo-se as medidas de dois lados ou a
medida de um lado mais a medida de um ângulo agudo, é possível calcular a medida dos demais lados
e ângulos. A área de um triângulo retângulo é dada pela metade do produto dos menores lados. A
relação entre os lados e ângulos de um triângulo retângulo é a base da trigonometria.
Elementos do triângulo retângulo:
Elementos de um triângulo retângulo. Os pontos A, B e C, os lados opostos a (hipotenusa), b e c(catetos) e as
projeções de b e c, me n.
Um triângulo retângulo é composto por quatro principais elementos:




Catetos;
Hipotenusa;
Altura relativa à hipotenusa;
Projeções dos catetos.
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 7
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Catetos:
Os catetos são os menores lados do triângulo retângulo. Eles formam o ângulo de 90°.
Altura relativa à hipotenusa:
A altura relativa à hipotenusa é a distância entre a hipotenusa e o vértice oposto.
Projeções dos catetos:
A altura relativa à hipotenusa divide-a em duas partes, denominadas projeções dos catetos.
Relações métricas do triângulo retângulo:
As relações métricas do triângulo retângulo são quatro. Os três triângulos formados ao traçar a altura
relativa à hipotenusa são retângulos e semelhantes.
Ilustração dos principais elementos do triângulo retângulo: aé a hipotenusa, b o cateto maior, c o cateto menor, h a
altura relativa à hipotenusa, m a projeção do cateto b e n a projeção do cateto c

A hipotenusa é igual à soma das projeções.
Por semelhança de triângulos, temos que:

O quadrado da altura relativa à hipotenusa é igual ao produto das projeções dos catetos.


:
O quadrado de um cateto é igual ao produto entre a sua projeção (que se encontra do seu lado)
e a hipotenusa.

:


:
O produto entre a hipotenusa e a altura relativa a ela é igual ao produto dos catetos.

:
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 8
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Teorema de Pitágoras:
O Teorema de Pitágoras diz que:
A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
— Pitágoras
ou, em linguagem matemática:
hipotenusa (AB)² = cateto (BC)² + cateto (CA)²
Relações trigonométricas do triângulo retângulo:
Outra maneira de calcular a medida dos lados de um triângulo retângulo é através da medida
de um ângulo e um lado, usando a Trigonometria. As principais relações trigonométricas
são: Seno, Cosseno e Tangente. Há outras três: Cotangente, Secante e Cossecante.
Seno de um ângulo:
É dado pela razão entre os lados que formam o outro ângulo agudo, dado pela ordem :
Cosseno de um ângulo:
Cosseno: É a razão entre a medida do cateto adjacente e a medida da hipotenusa e é dado
pela razão entre os lados que formam o próprio ângulo agudo, dado pela ordem::
Tangente de um ângulo:
É dado pela razão entre o Seno e o Cosseno de um ângulo, ou entre os catetos, dado
pela seguinte ordem::
Cotangente de um ângulo:
É dado pela razão entre o Cosseno e o Seno de um ângulo, ou entre os catetos,
dado pela seguinte ordem:
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 9
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Secante de um ângulo:
É dado pelo inverso do cosseno desse ângulo ou entre os lados que formam o
próprio ângulo, dado na seguinte ordem:
Cossecante de um ângulo:
É dado pelo inverso do seno desse ângulo ou entre os lados que formam o
outro ângulo agudo, dado na seguinte ordem:
Ângulos notáveis:
Grau
s
Radiano
s
0
0
sen
cos
tg
cotg
sec
cosse
c
30
45
60
90
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 10
trigonometrico.docx
Recredenciamento
Portaria MEC 347, de 05.04.2012 – DOU - 10.04.2012.
Circunferência inscrita num triângulo retângulo:
O diâmetro (d) de uma circunferência inscrita num triângulo rectângulo (a b c) é
igual à soma dos catetos, menos a hipotenusa, representado pela seguinte
fórmula:





cateto
cateto
hipotenusa
raio da circunferência inscrita
diâmetro da circunferência inscrita
Substituindo I e II em III, teremos
Como:
Ver também:



Triângulo
Teorema de Pitágoras
Trigonometria
Fonte: https://pt.wikipedia.org/wiki/Tri%C3%A2ngulo_ret%C3%A2ngulo
C o m p l e x o
d e
E n s i n o
S u p e r i o r
d e
C a c h o e i r i n h a
Rua Silvério Manoel da Silva, 160 – Bairro Colinas – Cep.: 94940-243 | Cachoeirinha – RS | Tel/Fax. (51) 33961000 | e-mail: [email protected]
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_v - circulo trigonometrico\pratica de ensino iii - quest_v 11
trigonometrico.docx