2013

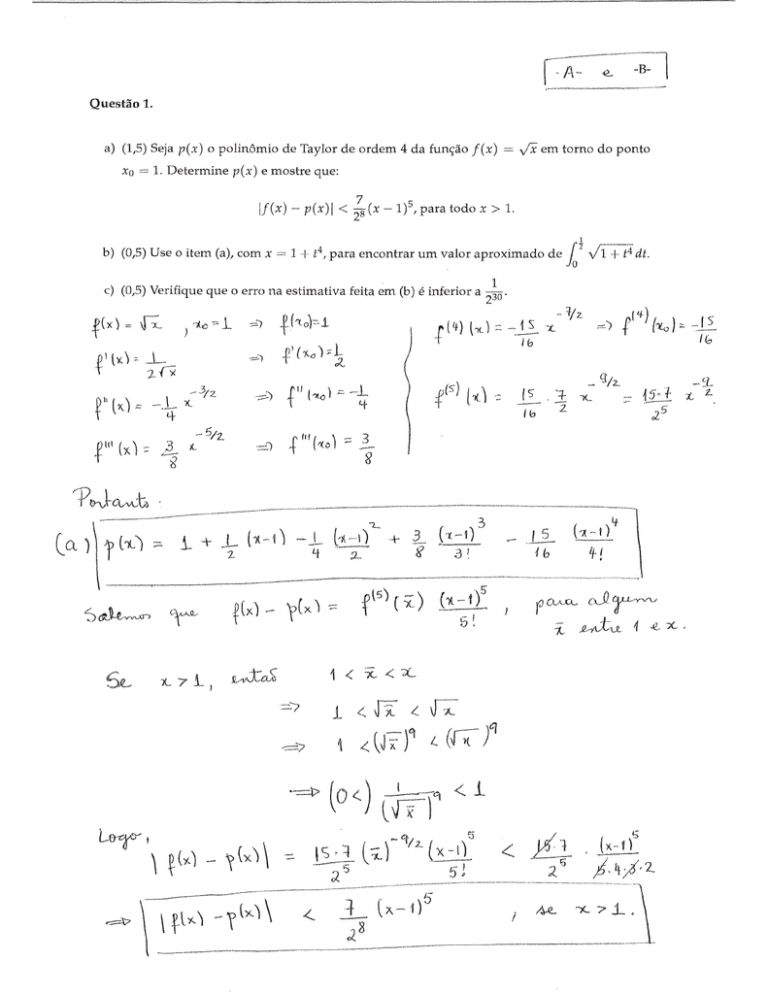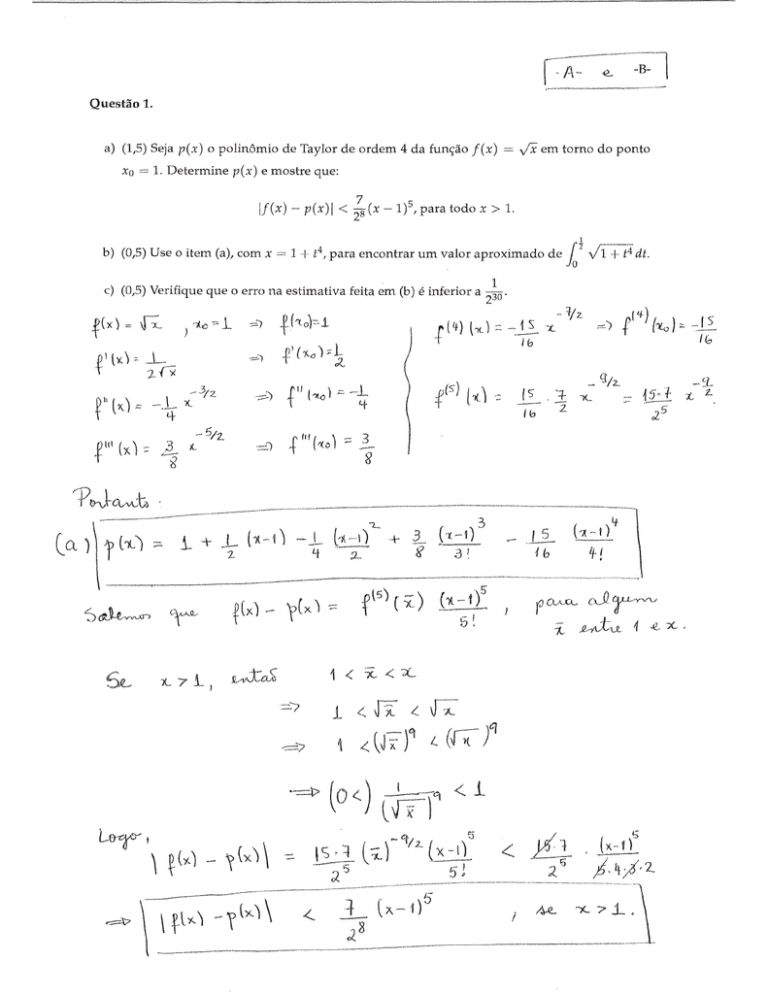
-AQuestão 2. Considere a função f ( x, y) = p
pelo ponto (3, 0).
x
3 + 2x − 3y2
e seja C a curva de nı́vel de f que passa
a) Usando o sistema de coordenadas abaixo:
i) (0,5) represente geometricamente o domı́nio de f ;
3 + 2x − 3y2 > 0 ⇒ x > 23 y2 −
3
2
⇒ D f = {( x, y) ∈ R2 : x > 32 y2 − 23 }
Ou seja, o domı́nio de f é a região interna da parábola x = 32 y2 −
ii) (1,0) faça um esboço da curva C .
x
= k.
Seja k ∈ Im f e considere p
3 + 2x − 3y2
Como (3, 0) ∈ C , então k = f (3, 0) = √3 = 1.
9
p
x = 3 + 2x − 3y2 (observe que x > 0)
x2
− 3y2
x2
+ 1 + 3y3
x −1
2
2
3
2
y
2
=1
=4 ⇒
+ √2
3
2 2
x −1
+ √y2
Ou seja, a curva C é parte da elipse 2
= 1, na qual x > 0.
= 3 + 2x
⇒
− 2x
(∗)
3
y
C
3
-3/2
Df
x
b) (1,0) Determine uma parametrização para a curva C , isto é, encontre um intervalo I e uma
função γ : I → R2 contı́nua cuja imagem é C .
Utilizando a relação fundamental da trigonometria em (∗), segue que uma parametrização
para a curva C é dada por
2
γ(t) = (1 + 2 cos t, √ sen t), com 1 + 2 cos t > 0
3
Portanto, cos t > − 12 , ou seja, t ∈ I =] −
2π 2π
3 , 3 [.
-Ac) (0,5) Decida se existe
lim
( x,y)→(0,1)
f ( x, y).
Considere a curva γ1 (t) = (t, 1), com t > 0, e a curva γ como no item (b).
Temos que
(a) lim f (γ1 (t)) = lim
t →0+
t →0+
√
t
3+2t−3
=0
(b) lim f (γ(t)) = lim 1 = 1 (γ é a curva de nı́vel 1 de f e γ(t) → (0, 1), quando t →
t→ 2π
3
t→ 2π
3
Portanto, NÃO existe
lim
( x,y)→(0,1)
f ( x, y).
2π
3 )
-BQuestão 2. Considere a função f ( x, y) = p
passa pelo ponto (6, 0).
x
12 + 4x − 12y2
e seja C a curva de nı́vel de f que
a) Usando o sistema de coordenadas abaixo:
i) (0,5) represente geometricamente o domı́nio de f ;
12 + 4x − 12y2 > 0 ⇒ x > 3y2 − 3 ⇒ D f = {( x, y) ∈ R2 : x > 3y2 − 3}
Ou seja, o domı́nio de f é a região interna da parábola x = 3y2 − 3
ii) (1,0) faça um esboço da curva C .
x
= k.
12 + 4x − 12y2
Como (6, 0) ∈ C , então k = f (6, 0) = √6 = 1.
36
p
x = 12 + 4x − 12y2 (observe que x > 0)
Seja k ∈ Im f e considere p
x2
= 12 + 4x
− 12y2
⇒
x2
− 4x
x −2 2
4
+ 4 + 12y3
y
= 16 ⇒
+ √2
3
2
2 2
Ou seja, a curva C é parte da elipse x−
+ √y2
= 1, na qual x > 0.
4
2
=1
(∗)
3
y
C
6
-3
Df
x
b) (1,0) Determine uma parametrização para a curva C , isto é, encontre um intervalo I e uma
função γ : I → R2 contı́nua cuja imagem é C .
Utilizando a relação fundamental da trigonometria em (∗), segue que uma parametrização
para a curva C é dada por
2
γ(t) = (2 + 4 cos t, √ sen t), com 2 + 4 cos t > 0
3
Portanto, cos t > − 12 , ou seja, t ∈ I =] −
2π 2π
3 , 3 [.
-Bc) (0,5) Decida se existe
lim
( x,y)→(0,1)
f ( x, y).
Considere a curva γ1 (t) = (t, 1), com t > 0, e a curva γ como no item (b).
Temos que
(a) lim f (γ1 (t)) = lim
t →0+
t →0+
√
t
12+4t−12
=0
(b) lim f (γ(t)) = lim 1 = 1 (γ é a curva de nı́vel 1 de f e γ(t) → (0, 1), quando t →
t→ 2π
3
t→ 2π
3
Portanto, NÃO existe
lim
( x,y)→(0,1)
f ( x, y).
2π
3 )
3 2
b) (1,0)
x y
lim
x6
(x,y)-t(O,O)
-
y4
~ t
(0,
(j.I~
d-).QA.~
(4t.d..~~;).) ~
~
~
0~(O,O)
("XI
)
••••
l' 1-\
QV\ t )
y~ =-~ (-t) :.
_l/ .... -l-"">o...•.
-t
-t
.•.• 1'0
~I
1°\
::= V
)
D
;J...
.Jl.3
0: ~
e.A
tA,j ~\O#Q)
l\
LQ-
~
0
(
(L\
3
2l/
JA
~
::j:.
(~I
N) ~
)
(0/
(x\ ~,-)~'"V~
..,~
-l QO.c0
(1.
J )
L-\
.r-
j'-)