MÓDULO 19 FRENTE 1 – MECÂNICA

C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 49
FRENTE 1 – MECÂNICA
MÓDULO 19
ATRITO
1. Um bloco de massa m = 2,0kg está em repouso sobre um plano
horizontal. Os coeficientes de atrito estático e dinâmico entre o bloco
e o plano de apoio valem, respectivamente, 0,40 e 0,30.
Considere g = 10,0m/s2 e despreze o efeito do ar.
→
Uma força horizontal constante F é aplicada sobre o bloco.
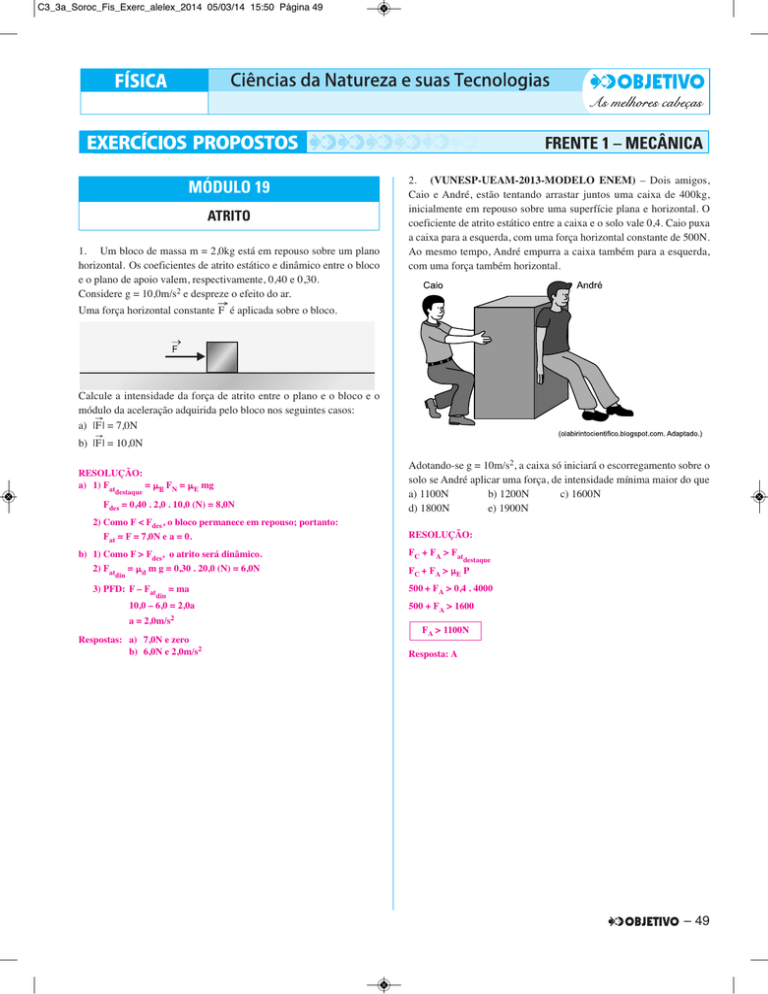
2. (VUNESP-UEAM-2013-MODELO ENEM) – Dois amigos,
Caio e André, estão tentando arrastar juntos uma caixa de 400kg,
inicialmente em repouso sobre uma superfície plana e horizontal. O
coeficiente de atrito estático entre a caixa e o solo vale 0,4. Caio puxa
a caixa para a esquerda, com uma força horizontal constante de 500N.
Ao mesmo tempo, André empurra a caixa também para a esquerda,
com uma força também horizontal.
Calcule a intensidade da força de atrito entre o plano e o bloco e o
módulo da aceleração adquirida pelo bloco nos seguintes casos:
→
a) |F | = 7,0N
→
b) |F | = 10,0N
RESOLUÇÃO:
a) 1) Fat
= Ε FN = E mg
destaque
Fdes = 0,40 . 2,0 . 10,0 (N) = 8,0N
2) Como F < Fdes , o bloco permanece em repouso; portanto:
Fat = F = 7,0N e a = 0.
b) 1) Como F > Fdes, o atrito será dinâmico.
2) Fat = d m g = 0,30 . 20,0 (N) = 6,0N
din
3) PFD: F – Fat
din
= ma
10,0 – 6,0 = 2,0a
Adotando-se g = 10m/s2, a caixa só iniciará o escorregamento sobre o
solo se André aplicar uma força, de intensidade mínima maior do que
a) 1100N
b) 1200N
c) 1600N
d) 1800N
e) 1900N
RESOLUÇÃO:
FC + FA > Fat
destaque
FC + FA > μE P
500 + FA > 0,4 . 4000
500 + FA > 1600
a = 2,0m/s2
Respostas: a) 7,0N e zero
b) 6,0N e 2,0m/s2
FA > 1100N
Resposta: A
– 49
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 50
3. (UECE-2013) – Um corredor parte do repouso com aceleração
constante em uma pista horizontal. Suponha que ele imponha uma aceleração tal que seus pés fiquem na iminência do deslizamento em relação ao solo. Se o coeficiente de atrito estático entre seu calçado e o
solo vale μ = 0,60, quantos metros o atleta percorre nos primeiros 2,0
segundos? Considere g = 10m/s2 e despreze o efeito do ar.
a) 2,0
b) 6,0
c) 10,0
d) 12,0
e) 24,0
2) Cálculo do tempo:
V = V0 + t
10,0 = 5,0T
T = 2,0s
Resposta: D
RESOLUÇÃO:
1) PFD: Fat = ma ⇒ μE mg = ma
0,60g = a ⇒
a = 6,0m/s2
γ
2) Δs = V0t + ––– t2
2
6,0
Δs = 0 + ––– (2,0)2 (m)
2
2. (VUNESP-FAMECA-2013) – Quando abandonado sobre um
plano inclinado de um ângulo θ (senθ = 0,60, cosθ = 0,80) com a
horizontal, um paralelepípedo desce o plano com velocidade constante.
Δs = 12,0m
Resposta: D
No mesmo local, onde a aceleração da gravidade tem módulo igual a
10m/s2, o paralelepípedo em questão, lançado no sentido ascendente
pela mesma trilha usada na descida, efetuará um movimento uniformemente retardado com aceleração escalar de valor absoluto, em m/s2,
igual a
a) 4,0
b) 6,0
c) 8,0
d) 10,0
e) 12,0
MÓDULO 20
PLANO INCLINADO
1. (UFJF-MG) – Um objeto de massa 5,0kg está apoiado sobre um
plano inclinado que faz com a horizontal um ângulo de 30 graus. Se
esse objeto for abandonado do repouso, depois de quanto tempo a sua
velocidade escalar atingirá 10,0m/s? Despreze as forças de atrito e o
efeito do ar. Considere g = 10,0m/s2.
a) 0,10s
b) 0,20s
c) 1,0s
d) 2,0s
e) 10,0s
RESOLUÇÃO:
RESOLUÇÃO:
1) Na descida: Fat = Pt
2)
Na subida: PFD: Pt + Fat = ma
2Pt = ma
2mg sen θ = ma
a = 2g sen θ
a = 20,0 . 0,60 (m/s2)
a = 12,0m/s2
Resposta: E
1) Cálculo da aceleração escalar:
PFD: Pt = ma
mg sen θ = ma
1
a = g sen = 10,0 · –– (m/s2)
2
a = 5,0m/s2
50 –
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 51
3. (UDESC-MODELO ENEM) – Um maratonista, ao final de seu
tratamento fisioterápico, é submetido a uma avaliação de resistência
física e força muscular. No teste de força muscular, o maratonista
deverá empurrar um bloco de 50 kg, em um sistema idêntico a um
plano inclinado, conforme ilustra a figura. Esse bloco deverá adquirir
uma aceleração com módulo igual a 0,50m/s2.
Considere: g = 10 m/s2; cos 60° = 0,50 e sen 60° = 0,90. Despreze o
efeito do ar.
Para essas condições, sabendo-se que o coeficiente de atrito cinético
→
entre o bloco e o plano vale 0,50, o módulo da força F que o maratonista deverá aplicar sobre o bloco vale:
a) 500N
b) 550N
c) 600N
d) 650N
e) 700N
RESOLUÇÃO:
MÓDULO 21
COMPONENTES DA RESULTANTE
1. (UECE-2013) – Em um primeiro experimento, uma partícula é
posta em movimento circular uniforme, em um plano horizontal, com
a realização de três voltas completas por minuto. A trajetória circular
é mantida por uma mola de constante elástica k1 que liga a partícula a
um ponto fixo. Em um segundo experimento, com a substituição da
mola por outra de mesmo comprimento natural e constante elástica k2,
a partícula percorre a mesma trajetória também com movimento
circular uniforme, porém, realiza o dobro de voltas em um minuto.
Assim, é correto afirmar-se que
a) k2 = 2k1
b) k2 = 3k1
c) k2 = 4k1
d) k2 = 5k1
e) k2 = 6k1
RESOLUÇÃO:
Fe = Fcp
k1 x = m ω2 R = m (2πf) 2 R
kx = m . 4π2 f2 . R
k1 x = m 4π2 . f2 R
k2 x = m 4π2 (2f)2 R
k2
–––
=4 ⇒
k1
k2 = 4k1
Resposta: C
1)
Pt = P sen = 500 . 0,90 (N) = 450N
2)
Fat = P cos Fat = 0,50 . 500 . 0,50(N) = 125N
3)
PFD = F – (Pt + Fat) = ma
F – 575 = 50 . 0,50
F = 575 + 25 (N)
F = 600N
Resposta: C
– 51
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 52
2. (VUNESP-UEAM-2013-MODELO ENEM) – O macaco-barrigudo é um primata encontrado na floresta amazônica, principalmente
na parte inundada da floresta, ao norte dos rios Negro e Solimões. A
figura mostra um desses macacos, com 10kg, brincando pendurado em
um cipó inextensível preso a um galho, descrevendo uma circunferência de centro C contida em um plano horizontal, em movimento
uniforme. O cipó que o prende ao galho está inclinado de um ângulo θ
em relação à vertical. C
3. (UFT-MODELO ENEM) – Durante uma apresentação circense,
um artista se apresenta com sua motocicleta em um globo da morte de
raio R. Num dado instante da apresentação, a motocicleta passa pelo
ponto mais alto do globo, conforme ilustrado na figura. Para não cair
verticalmente, a motocicleta deve possuir uma velocidade escalar
mínima V. Considere M a massa total (motocicleta + artista), Fn a
intensidade da força normal e g o módulo da aceleração da gravidade.
(zaroio.net. Adaptado.)
Desprezando-se a resistência do ar, sabendo-se que sen θ = 0,6 e
cos θ = 0,8 e adotando-se g = 10m/s2, a intensidade da força de tração
no cipó que prende o macaco ao galho e a intensidade da resultante
centrípeta valem, respectivamente
a) 175N e 125N
b) 100N e 150N
c) 150N e 75N
d) 125N e 75N
e) 125N e 150N
A expressão correta da velocidade escalar mínima é:
a) Rg
d)
RESOLUÇÃO:
1) Ty = P = mg = 100N
Ty
2) cos θ = –––
T
100
0,8 = ––– ⇒
T
(Fn + Mg)R
––––––––––
M
b) MRg
e)
RESOLUÇÃO:
T = 125N
FN + P = Fcp
mV2
FN + mg = ––––
R
V = Vmín quando FN = 0
Tx
3) sen θ = –––
T
Fcp
0,6 = –––
⇒
125
Resposta: D
Fcp = 75N
2
mVmín
mg = –––––––
R
Vmín = Rg
Resposta: A
52 –
(Fn – Mg)R
––––––––––
M
c)
Rg
–––
M
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 53
MÓDULO 22
EXERCÍCIOS DE FORÇA CENTRÍPETA
1. (FUNDAÇÃO CARLOS CHAGAS) – Num trecho de uma pista
de automobilismo, há uma lombada cujo raio de curvatura é de 50m.
Um carro passa pelo ponto mais alto da elevação com velocidade de
módulo V, de forma que a interação entre o veículo e o solo (peso
aparente), neste ponto, tem intensidade igual a um quinto do seu peso.
Adote g = 10m/s2 e não considere efeito do ar.
Nestas condições, em m/s, o valor de V é:
a) 10
b) 20
c) 30
d) 40
e) 50
2
Considere uma roda-gigante e uma pessoa de peso P sentada em
uma das cadeiras descrevendo movimento uniforme em uma trajetória
circular de raio R em um plano vertical.
Quando a cadeira passa pelo ponto mais alto (A), a pessoa recebe do
assento uma força vertical para cima de intensidade NA. Quando a
cadeira passa pelo ponto mais baixo (B), a pessoa recebe do assento
uma força vertical para cima de intensidade NB.
RESOLUÇÃO:
Determine
a) o peso P da pessoa em função de NA e NB;
b) a intensidade da força resultante na pessoa em função de NA e NB;
No ponto A:
RESOLUÇÃO:
a)
ponto A: Fcp = P – NA (1)
P – FN = Fcp
A
mg
mV2
mg – –––– = ––––
5
R
ponto B: Fcp = NB – P (2)
(1) = (2): P – NA = NB – P
4g
V2
––– = –––
5
R
V=2
gR
–––
5
V=2
10 · 50
––––– (m/s)
5
V = 20m/s
Resposta: B
2P = NB + NA
NB + NA
P = ––––––––––
2
b) Fcp = P – NA (1)
Fcp = NB – P (2)
(1) + (2): 2Fcp = NB – NA
NB – NA
Fcp = ––––––––––
2
NB + NA
Respostas: a) P = ––––––––––
2
NB – NA
b) FR = Fcp = ––––––––
2
– 53
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 54
3. (FUVEST-TRANSFERÊNCIA-2013) – Um cavalo corre em um
picadeiro de circo com 16,0m de diâmetro, plano e horizontal, em que
o coeficiente de atrito é = 0,80. O módulo da velocidade máxima
que ele pode manter, ao mover-se em círculo no picadeiro, é
a) 4,0m/s
b) 6,0m/s c) 8,0m/s d) 10,0m/s e) 14,0m/s
Adote g = 10,0m/s2 para o módulo da aceleração local da gravidade.
RESOLUÇÃO:
MÓDULO 23
TRABALHO
1. (FUVEST) – Um menino puxa, com uma corda, na direção
horizontal, um cachorro de brinquedo formado por duas partes, A e B,
ligadas entre si por uma mola, como ilustra a figura adiante. As partes
A e B têm, respectivamente, massas mA = 0,5kg e mB = 1,0kg, sendo
= 0,30 o coeficiente de atrito cinético entre cada parte e o piso. A
constante elástica da mola é k = 10N/m e, na posição relaxada, seu
comprimento é x0 = 10cm. O conjunto se move com velocidade
constante de módulo V = 0,10m/s.
1) FN = P = m g
mV2
2) Fat = Fcp = –––––
R
3) Fat FN
mV2
–––––– mg
R
V2 g R
V gR
Vmáx = gR
Nessas condições, determine
a) o módulo T da força exercida pelo menino sobre a parte B;
b) o trabalho W realizado pela força que o menino faz para puxar o
brinquedo por 2,0 minutos;
NOTE E ADOTE
Módulo da aceleração da gravidade no local: g = 10 m/s2
Despreze a massa da mola.
RESOLUÇÃO:
Vmáx = 0,80 · 10,0 · 8,0 m/s
Vmáx = 8,0m/s
Resposta: C
a) Sendo a velocidade constante, a força resultante no sistema (cachorromola) é nula, portanto:
T = fat + fat = (PA + PB)
A
B
T = 0,30 . 15 (N)
T = 4,5 N
b) 1) Cálculo da distância percorrida:
Δs = V Δt (MU)
Δs = 0,10 . 2,0 . 60 (m) = 12 m
2) Cálculo do trabalho:
W = T . Δs
W = 4,5 . 12 (J)
W = 54 J
Respostas: a) T = 4,5 N
b) W = 54 J
54 –
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 55
(UFRGS-2013) – Instrução: As questões 2 e 3 referem-se ao enunciado
abaixo.
Um estudante movimenta um bloco homogêneo de massa M, sobre
uma superfície horizontal, com forças de mesmo módulo F, conforme
representa a figura abaixo.
4. (UECE) – Uma partícula de massa m se desloca em linha reta do
ponto A ao ponto B, retornando em seguida ao ponto de partida. Sobre
ela atuam três forças: uma de atrito, com módulo constante; outra, com
módulo, direção e sentido constantes; e uma terceira não especificada.
Sobre o trabalho realizado pelas duas primeiras forças entre os pontos
inicial e final da trajetória, pode-se afirmar corretamente que é
a) nulo para a força de atrito e não nulo para a outra força.
b) não nulo para a força de atrito e nulo para a outra força.
c) nulo para as duas forças.
d) não nulo para as duas forças.
RESOLUÇÃO:
Para a força constante, o trabalho será nulo porque o deslocamento vetorial
é nulo.
Para a força de atrito, o trabalho é negativo porque a força de atrito tem
sentido oposto ao deslocamento e vai transformar energia mecânica em
térmica.
Resposta: B
Em X, o estudante empurra o bloco; em Y, o estudante puxa o bloco;
em Z, o estudante empurra o bloco com força paralela ao solo.
2. A força normal exercida pela superfície é, em módulo, igual ao
peso do bloco
a) apenas na situação X.
b) apenas na situação Y.
c) apenas na situação Z.
d) apenas nas situações X e Y.
e) em X, Y e Z.
MÓDULO 24
TEOREMA DA ENERGIA
CINÉTICA E MÉTODO GRÁFICO
RESOLUÇÃO:
Fy = F sen α
Em X: FN = P + F sen α
Em Y: FN = P – Fsen α
Em Z: FN = P
Resposta: C
3. O trabalho realizado pelo estudante para mover o bloco nas
situações apresentadas, por uma mesma distância d, é tal que
a) Wx = Wy = Wz.
b) Wx = Wy < Wz.
c) Wx > Wy > Wz.
d) Wx > Wy = Wz.
e) Wx < Wy < Wz.
RESOLUÇÃO:
τ + F d cos τx = τy = Fd cos τz = F d cos 0° = F d
1. (CESGRANRIO-2013) – Uma partícula de 30,0g é deixada cair,
a partir do repouso, de uma altura de 2,0m. A energia cinética da
partícula, quando chega ao solo, é de 0,40J.
Qual é o trabalho realizado, em J, pela resistência do ar que dissipa
parte da energia mecânica do sistema partícula-terra?
a) –0,10 b) –0,20
c) –0,30
d) –0,40
e) –0,60
Dado: módulo da aceleração da gravidade g = 10,0m/s2
RESOLUÇÃO:
TEC: τtotal = ΔEcin
mV2
τP + τar = ––––
2
mV2
mgH + τar = ––––
2
0,030 . 10,0 . 2,0 + τar = 0,40
0,60 + τar = 0,40
τar = –0,20J
Resposta: B
τz > τx = τy
Resposta: B
– 55
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 56
2. (VUNESP-FAMECA-2013) – A Rodovia dos Imigrantes tem, na
pista de descida da Serra do Mar, três túneis sequenciais com poucas
curvas de grande raio. O desnível entre os pontos de entrada e de saída
dos túneis é cerca de 600m. A velocidade escalar máxima ali permitida
é de 80km/h, o que garante boas condições de segurança aos seus
usuários. Um carro, de massa total 1500kg, percorre integralmente esse
trecho com a máxima velocidade escalar permitida. A aceleração da
gravidade local é admitida com módulo de 10m/s2. Determine:
a) o trabalho realizado pela força peso do carro.
b) o trabalho realizado pela resultante das forças dissipativas que
atuam sobre o carro.
3. (UFTM-MG-2013) – O funcionário de um armazém, responsável
pela reposição de produtos, empurra, a partir do repouso e em movimento retilíneo, um carrinho com massa total de 350kg sobre uma
superfície plana e horizontal.
RESOLUÇÃO:
Em um determinado trecho de 8,0m de comprimento, ele dá três empurrões consecutivos no carrinho, exercendo uma força horizontal para
a direita, cuja intensidade é representada no gráfico 1, em função da
posição do carrinho. Nesse mesmo trecho, atua sobre o carrinho uma
força de atrito de intensidade constante, igual a 100N.
a)
τP + mgH
τP = 1500 . 10 . 600 (J)
τP = 90 . 105J
τP = 9,0 . 106J
b) TEC:
τP + τr = ΔEcin
9,0 . 106 + τr = 0
τr = –9,0 . 106J
Respostas: a) 9,0 . 106J
b) –9,0 . 106J
Calcule:
a) a intensidade máxima da força resultante que atuou no carrinho nos
primeiros 2,0m de deslocamento.
b) a velocidade escalar atingida pelo carrinho ao final dos 8,0m.
RESOLUÇÃO:
a) x = 2,0m ⇒ F = 500N e Fat = –100N
FR = F + Fat ⇒
b) 1)
FR(máx) = 400N
τ = área (F x d)
τF = 3 . 2,0 .
500
––– (J) = 1500J
2
τat = –100 . 8,0 = –800J
2)
TEC: τtotal = Ecin
mV2
mV 2
τF + τat = –––– – ––––0
2
2
350
1500 – 800 = –––– V2 ⇒ V2 = 4,0 ⇒
2
Respostas: a) 400N
b) 2,0m/s
56 –
V = 2,0m/s
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 57
FRENTE 2 – ÓPTICA E ONDULATÓRIA
MÓDULO 19
REFRAÇÃO (II) – REFLEXÃO TOTAL
1. (UFPE) – Um raio de luz incide na parte curva de um cilindro de
plástico de seção semicircular, formando um ângulo θi com o eixo de
simetria. O raio emerge na face plana, formando um ângulo θr com o
mesmo eixo. Um estudante fez medidas do ângulo θr em função do
ângulo θi e o resultado está mostrado no gráfico θr versus θi. Determine
o índice de refração deste plástico.
Na figura, um raio luminoso monocromático incide perpendicularmente na face CA, sofre reflexões internas totais, respectivamente nas
faces BC e AB, e emerge perpendicularmente à face CA. Se o prisma
está imerso no ar (índice absoluto de refração igual a 1,0), pode-se
afirmar que n é tal que:
3 2
a) n > ––––––
4
2 3
b) n > ––––––
3
d) n > 3
e) n > 2
3
c) n > –––
2
RESOLUÇÃO:
RESOLUÇÃO:
(I) Conforme o gráfico, para θr = 90° (emergência rasante), tem-se θi = 30°.
Nesse caso, θi é o ângulo limite do dioptro plástico-ar.
(II)Lei de Snell: n sen θi = nAr sen θr
1
n sen 30° = 1 . sen 90° ⇒ n . ––– = 1
2
Da qual:
n=2
Resposta: 2
Para que o prisma opere nas condições especificadas, o ângulo de incidência
da luz na face AB, isto é, 30° (veja a figura) deve superar o ângulo limite L
do dioptro prisma-ar. Logo:
30° > L ⇒ sen 30° > sen L
1
nAr
1
1,0
––– > –––– ⇒ ––– > –––
2
n
2
n
2. Uma das principais utilidades do prisma óptico é o seu emprego
como sistema de reflexão total. Nessa operação, o prisma pode
substituir com vantagens os espelhos planos, pois pode ter um poder
refletor bem maior que o dos espelhos e, além disso, está livre da deterioração que ocorre na película de prata dos espelhos, por oxidação.
Da qual:
n>2
Resposta: E
No esquema a seguir, está representado o corte transversal de um prisma óptico ABC de índice absoluto de refração igual a n, utilizado em
um modelo de máquina fotográfica para deslocar lateralmente a luz.
– 57
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 58
3. (UFBA) – As fibras ópticas são longos fios finos, fabricados com
vidro ou materiais poliméricos, com diâmetros da ordem de
micrômetros até vários milímetros, que têm a capacidade de transmitir
informações digitais, na forma de pulsos de luz, ao longo de grandes
distâncias, até mesmo ligando os continentes através dos oceanos. Um
modo de transmissão da luz através da fibra ocorre pela incidência de
um feixe de luz, em uma das extremidades da fibra, que a percorre por
meio de sucessivas reflexões. As aplicações das fibras ópticas são
bastante amplas nas telecomunicações e em outras áreas, como a
medicina, por exemplo. Uma vantagem importante da fibra óptica, em
relação aos fios de cobre, é que nela não ocorre interferência
eletromagnética.
1
cos α = –––––
3
Da qual:
(III)
Lei de Snell aplicada à refração de entrada da luz:
nar sen i = n sen r
nar sen i = n sen (90° – α)
nar sen i = n cos α ⇒ 1 . sen i =
1
3
––– . ––––
2
3
1
1
3
2
sen i = –––– . –––– ⇒ sen i = –––– = ––––
2
2
3
2
Da qual:
i = 45°
Resposta: 45°
MÓDULO 20
LENTES ESFÉRICAS I –
CONSTRUÇÕES GRÁFICAS
Supondo-se que uma fibra óptica se encontra imersa no ar (nar = 1) e
3
––– , calcule o
2
maior ângulo de incidência de um raio de luz em relação ao eixo da
fibra, para que ele seja totalmente refletido pela parede cilíndrica.
1. (UPE-2013) – Sabe-se que uma lente biconvexa, de índice de
refração n, é convergente quando imersa num meio de índice de
refração nA e divergente quando imersa num meio de índice de refração
nB. Logo, é correto afirmar que
a) nA < n < nB
b) nA < nB < n
c) n < nA < nB
d) n < nA = nB
e) n = nA > nB
que o índice de refração da fibra óptica é igual a
RESOLUÇÃO:
(I) A lente é convergente:
RESOLUÇÃO:
(I)
Na situação limítrofe, ocorre emergência rasante e reflexão (não
total) na interface fibra-ar, como representa o esquema abaixo,
em que α é o ângulo-limite do dioptro.
Lei de Snell:
n sen α = nar sen 90°
3
––– sen α = 1
2
sen α =
(II)
2
––––
3
sen2 α + cos2 α = 1
58 –
(II)A lente é divergente:
2
–––
3
2
2
+ cos2 α = 1 ⇒ cos2α = 1 – –––
3
Logo:
Resposta: A
nA < n < nB
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 59
2. (UNICENTRO-RJ) – A figura mostra o esquema da associação
de duas lentes convergentes, L1 e L2, coaxiais, afastadas de uma
distância igual a 0,5m. Observa-se que, incidindo na lente L1 um pincel
cilíndrico de luz monocromática com 2,5cm de diâmetro e coincidente
com o eixo óptico, emerge da lente L2 um pincel luminoso cilíndrico
com 10,0cm de diâmetro, coincidente com o eixo óptico do sistema.
3. (MACK-2013) – Em um experimento de óptica, na sala de aula,
coloca-se um objeto real à distância de 6 cm do centro óptico de uma
lente biconvexa de distância focal 4 cm. Sendo observadas as
condições de Gauss, a distância entre esse objeto e sua imagem
projetada numa parede será de
a) 6cm
b) 9cm
c) 12cm
d) 15cm
e) 18cm
RESOLUÇÃO:
(I) Abscissa do objeto: p = 6cm
Distância focal: f = 4cm
Cálculo da abscissa da imagem p’:
1
1
1
––– + ––– = ––– (Equação de Gauss)
p’
p
f
1
1
1
––– + ––– = –––
p’
6
4
1
1
1
6–4
2
––– = ––– – ––– = ––––– = –––
p’
4
6
24
24
p’ = 12cm
Com base nas observações, a distância focal da lente L2, medida em
cm, é igual a
a) 15,0
b) 20,0
c) 25,0
d) 30,0
e) 40,0
(II)Na figura abaixo, estão posicionados a lente, o objeto e a respectiva
imagem.
RESOLUÇÃO:
A situação proposta constitui um sistema óptico afocal e está esquematizada, fora de escala, a seguir.
d = 6 + 12 (cm)
Da qual:
d = 18cm
Resposta: E
(I)
Semelhança de triângulos:
f1
f2
–––
= ––––
⇒ f1 = 0,25f2
2,5
10,0
a
(II) Da figura: f1 + f2 = 50,0 b
(III) Substituindo-se a em b, vem:
0,25f2 + f2 = 50,0 ⇒ 1,25f2 = 50,0 ⇒
f2 = 40,0cm
Resposta: E
– 59
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 60
MÓDULO 21
LENTES ESFÉRICAS II –
ESTUDO ANALÍTICO E VERGÊNCIA DE UMA LENTE
2. (UNESP) – Para observar detalhes de um selo, um filatelista
utiliza uma lente esférica convergente funcionando como lupa. Com
ela, consegue obter uma imagem nítida e direita do selo, com as
dimensões relativas mostradas na figura.
1. (UFPR-2013) – Um objeto movimenta-se com velocidade
constante ao longo do eixo óptico de uma lente delgada positiva de
distância focal f = 10cm. Num intervalo de 1s, o objeto se aproxima da
lente, indo da posição 30cm para 20cm em relação ao centro óptico da
lente. V0 e Vi são as velocidades médias do objeto e da imagem,
respectivamente, medidas em relação ao centro óptico da lente.
Desprezando-se o tempo de propagação dos raios de luz, é correto
concluir que o módulo da razão V0/Vi é:
a) 2/3
b) 3/2
c) 1
d) 3
e) 2
RESOLUÇÃO:
(I)
.p1 – p0.
.20 – 30.
= –––––––– (cm/s)
Para o objeto: .V0. = ––––––––
t
1,0
Da qual: .V0. = 10cm/s
(II) Para a imagem:
1
1
1
Equação de Gauss: ––– + ––– = –––
p
p’
f
1
1
1
Em t0 = 0: ––– + ––– = –––
10
30
p0’
1
1
3–1
1
––– = ––– – ––– = ––––– ⇒ p’0 = 15cm
10
30
30
p0’
1
1
1
Em t1 = 1,0s: ––– + ––– = –––
10
20
p’1
1
1
2–1
1
––– = ––– – ––– = ––––– ⇒ p’1 = 20cm
10
20
20
p’1
.p’1 – p’0.
.20 – 15.
= –––––––– (cm/s)
.Vi. = ––––––––
t
1,0
Da qual:
(III)
.Vi. = 5cm/s
V
V
= ––– = –––– = 2
––––
5
V V
0
i
Resposta: E
60 –
10
0
i
Considerando-se que o plano que contém o selo é paralelo ao da lente
e sabendo-se que a distância focal da lente é igual a 20cm, calcule os
módulos das distâncias do selo à lente e da imagem do selo à lente.
RESOLUÇÃO
1) De acordo com a figura:
Aumento linear transversal: A = 2
20
f
2) A = –––– ⇒ 2 = –––––
20 – p
f–p
40 – 2p = 20 ⇒ 2p = 20 ⇒
p = 10cm
p’
p’
3) A = – ––– ⇒ 2 = – ––– ⇒ p’ = –20cm
p
10
Respostas: distância do objeto à lente: 10cm;
distância da imagem à lente: 20cm
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 61
3. (FACID-PI-2013) – A lente em questão é utilizada para observar
atentamente uma formiguinha.
Ah, Bidu, estou
apaixonada pelo
elefante, mas ele
nem me olha!
Você não
podia me
dar uma
mãozinha?
4. (FUVEST-2013) – A extremidade de uma fibra ótica adquire o
formato arredondado de uma microlente ao ser aquecida por um laser,
acima da temperatura de fusão. A figura abaixo ilustra o formato da
microlente para tempos de aquecimento crescentes (t1 < t2 < t3).
Claro!
Deixe
comigo!
Considere as afirmações:
I. O raio de curvatura da microlente aumenta com tempos crescentes
de aquecimento.
II. A distância focal da microlente diminui com tempos crescentes
de aquecimento.
III. Para os tempos de aquecimento apresentados na figura, a microlente é convergente.
Está correto apenas o que se afirma em
a) I.
b) II.
c) III.
d) I e III.
e) II e III.
Bidu deseja comprar uma lente em que a imagem da formiguinha seja
direta e ampliada cinco vezes. Se a lente está a 20 cm da formiga, então
a vergência dela é de
a) 1,0 “grau”
b) 2,0 “graus”
c) 3,0 “graus”
d) 4,0 “graus”
e) 5,0 “graus”
RESOLUÇÃO:
(I)
f
A = –––––
f–p
f
5 = –––––
f – 20
5f – 100 = f ⇒ 4f = 100
f = 25cm = 0,25m
1
1
(II) V = ––– ⇒ V = ––––– (di)
f
0,25
V = 4,0 di
Resposta: D
Note e adote:
A luz se propaga no interior da fibra ótica, da esquerda para a
direita, paralelamente ao seu eixo.
A fibra óptica está imersa no ar e o índice de refração do seu
material é 1,5.
RESOLUÇÃO:
(I) FALSA. O raio de curvatura da microlente diminui com o tempo de
aquecimento. Sendo R o respectivo raio de curvatura, tem-se:
Se t3 > t2 > t1 ⇒ R3 < R2 < R1
(II) VERDADEIRA. Pela Equação de Halley (equação dos fabricantes de
lentes) e considerando-se, por simplicidade, uma lente plano-convexa,
a distância focal fica determinada por:
1
1
–– = (n – 1) –– ⇒
f
R
R
f = ––––––
n–1
em que n é o índice de refração relativo da lente em relação ao ar.
Para t3 > t2 > t1, tem-se R3 < R2 < R1.
Logo:
f3 < f2 < f1
(III) VERDADEIRA. A face convexa da lente tem raio de curvatura algebricamente positivo. Sendo R > 0 e n > 0, tem-se f > 0, o que
caracteriza o comportamento convergente da lente.
Resposta: E
– 61
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 62
RESOLUÇÃO:
MÓDULO 22
I. VERDADEIRA.
ÓPTICA DA VISÃO
II. FALSA. Na refração, a trajetória da luz nem sempre é desviada. A frequência da luz não se altera, mas a velocidade de propagação e o comprimento de onda variam na proporção inversa do índice de refração.
1. (UFSC-2013) – Fazendo-se uma análise simplificada do olho
humano, pode-se compará-lo a uma câmara escura. Fazendo-se uma
análise cuidadosa, ele é mais sofisticado que uma câmera fotográfica
ou filmadora. A maneira como o olho controla a entrada de luz e
trabalha para focalizar a imagem para que ela seja formada com nitidez
na retina é algo espetacular! A figura abaixo apresenta, de maneira
esquemática, a estrutura do olho humano e a forma pela qual a luz que
parte de um objeto chega à retina para ter a sua imagem formada.
III.FALSA. A luz refrata-se do ar para a córnea, da córnea para o humor
aquoso, do humor aquoso para o cristalino e do cristalino para o humor
vítreo.
IV. VERDADEIRA.
V. VERDADEIRA.
VI. FALSA. A lente corretiva é convergente.
Resposta: proposições corretas: I, IV e V
2. (UFRN-2013) – Durante uma consulta ao seu médico oftalmologista, um estudante obteve uma receita com as especificações dos
óculos que ele deve usar para corrigir seus defeitos de visão. Os dados
da receita estão apresentados no quadro abaixo.
Esférica Cilíndrica
(dioptrias) (dioptrias)
Na tabela abaixo, é apresentado o índice de refração de cada uma das
partes do olho.
Parte do olho
Índice de refração
Córnea
1,37 a 1,38
Humor aquoso
1,33
Cristalino
1,38 a 1,41
Humor vítreo
1,33
Disponível em: <http://adventista.forumbrasil.net/t1533-sistema-optico-olhohumano-novo-olhar-sobre-a-visao-mais-complexidade>. [Adaptado] Acesso
em: 18 jul. 2012.
Com base no exposto, assinale a(s) proposição(ões) correta(s).
I. A imagem do objeto formada na retina é real, invertida e menor,
o que nos leva a afirmar que o conjunto cornea-cristalino é uma
lente de comportamento convergente.
II. O fenômeno da refração da luz é garantido pelo desvio da
trajetória da luz, sendo mantidas constantes todas as outras
características da luz.
III. A refração da luz só ocorre no cristalino, cujo índice de refração
é diferente do índice de refração do humor aquoso e do humor
vítreo.
IV. A miopia é um problema de visão caracterizado pela formação da
imagem antes da retina, sendo corrigido com uma lente de
comportamento divergente.
V. A presbiopia, popularmente chamada de “vista cansada”, é um
problema de visão similar à hipermetropia, sendo corrigido com
uma lente de comportamento convergente.
VI. A hipermetropia é um problema de visão caracterizado pela
formação da imagem depois da retina, sendo corrigido com uma
lente de comportamento divergente.
62 –
Eixo
D.P.
OD
Para Longe
OE
OD
+ 2,0
OE
+ 2,0
Para Perto
Em suas aulas de Física, ele havia aprendido como se formam as
imagens no olho hipermétrope e no míope, as quais estão representadas
nas figuras I e II abaixo.
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 63
Sabendo-se que a dioptria, D, popularmente conhecida como “grau da
lente”, é determinada pelo inverso da distância focal f, medida em
1
metros, isto é, D = ––– , é correto afirmar que o estudante é
f
RESOLUÇÃO:
Como as lentes corretivas prescritas ao estudante são positivas (convergentes), sem defeito visual, em ambos os olhos, é hipermetropia.
a) hipermétrope, e as lentes de seus óculos devem ter distância focal
igual a 0,5m.
b) hipermétrope, e as lentes de seus óculos devem ter distância focal
igual a 2,0m.
c) míope, e as lentes de seus óculos devem ter distância focal com
módulo igual a 0,5m.
d) míope, e as lentes de seus óculos devem ter distância focal com
módulo igual a 2,0m.
Resposta: A
1
1
D = ––– ⇒ 2 = ––– ⇒
f
f
f = 0,50m
MÓDULO 23
NOÇÕES GERAIS DE ONDAS
1. (ENEM) – Nossa pele possui células que reagem à incidência de luz ultravioleta e produzem uma substância chamada melanina, responsável
pela pigmentação da pele. Pensando em se bronzear, uma garota vestiu um biquíni, acendeu a luz de seu quarto e deitou-se exatamente abaixo da
lâmpada incandescente. Após várias horas ela percebeu que não conseguiu resultado algum.
O bronzeamento não ocorreu porque a luz emitida pela lâmpada incandescente é de
a) baixa intensidade.
b) baixa frequência.
c) um espectro contínuo.
d) amplitude inadequada.
e) curto comprimento de onda.
RESOLUÇÃO:
O espectro eletromagnético emitido por uma lâmpada incandescente é composto principalmente por radiações infravermelhas e luz visível, de frequências
menores que as das radiações ultravioleta, exigidas no bronzeamento.
Professor:
É recomendável neste momento discorrer um pouco sobre o espectro eletromagnético.
(Imagem: http://refensdafisica.tumblr.com/post/19975814934/espectro-eletromagnetico)
Resposta: B
– 63
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 64
2. (UFRN-2013) – Quando olhamos para o céu noturno, vemos uma
grande quantidade de estrelas, muitas das quais se encontram a dezenas
e até a centenas de anos-luz de distância da Terra. Na verdade, estamos
observando as estrelas como elas eram há dezenas, centenas ou até
milhares de anos, e algumas delas podem nem mais existir atualmente.
Esse fato ocorre porque
a) a velocidade da luz no vácuo é infinita e não depende do movimento
relativo entre fontes e observadores.
b) a velocidade da luz no vácuo, apesar de ser muito grande, é finita e
depende do movimento relativo entre fontes e observadores.
c) a velocidade da luz no vácuo, apesar de ser muito grande, é finita e
não depende do movimento relativo entre fontes e observadores.
d) a velocidade da luz no vácuo é infinita e depende do movimento
relativo entre fontes e observadores.
RESOLUÇÃO:
2.o Postulado de Einstein, da Teoria da Relatividade:
“A velocidade da luz no vácuo tem o mesmo valor (c 300 000km/s) em
relação a qualquer referencial inercial.”
Observe a situação esquematizada abaixo:
3. (UFGD-2013) – As ondas sonoras se propagam com diferentes
velocidades em diferentes meios materiais. Sabendo-se que na água a
velocidade de propagação do som é de 1400 m/s, quanto tempo o sinal
do sonar de um navio em repouso levará para ir até um obstáculo
situado 14km à sua frente e retornar à embarcação?
a) 2s
b) 5s
c) 10s
d) 20s
e) 40s
RESOLUÇÃO:
2 . 1400
D
2d
V = ––– ⇒ V = –––– ⇒ 1400 = ––––––––
T
T
T
Da qual:
Resposta: D
No exemplo, as naves A e B descrevem MRU em sentidos opostos com
velocidades de módulos respectivamente iguais a 0,6c e 0,8c, em que c é a
intensidade da velocidade da luz no vácuo.
Deve-se notar nesse caso que a velocidade da nave A medida em relação à
nave B não atinge o valor c, muito menos o valor 1,4c, como se poderia
imaginar de maneira simplista.
O cálculo utilizado nesse contexto requer elementos relativísticos.
Resposta: C
64 –
T = 20s
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:50 Página 65
MÓDULO 24
EQUAÇÃO FUNDAMENTAL DA ONDULATÓRIA
V = f
1. (INTERNATIONAL JUNIOR SCIENCE OLYMPIAD-IJSL) – Em
duas cordas elásticas idênticas, tracionadas por forças de mesma
intensidade, são produzidas duas ondas harmônicas progressivas, A e
B. As figuras representam as formas das cordas num determinado
instante.
Calcule o intervalo de tempo, em unidades do Sistema Internacional,
que a onda leva para percorrer uma distância de 5m na corda.
a) 1,25
b) 12,5
c) 2,5
d) 25
e) 100
RESOLUÇÃO:
I) Da Equação fundamental da ondulatória:
λ
V = λ f ⇒ V = –––
T
Sendo T = 0,05s e λ = 0,2m, a velocidade de propagação do pulso fica
determinada fazendo-se:
0,2
V = –––– (m/s) ⇒
0,05
V = 4,0m/s
II) O movimento de propagação do pulso é uniforme, logo:
Δs
5,0
V = ––– ⇒ 4,0 = –––– ⇒
Δt
Δt
Δt = 1,25s
Resposta: A
Pode-se afirmar que:
a) As ondas possuem mesma amplitude.
b) Os pontos das cordas oscilam com a mesma frequência.
c) As ondas se propagam com a mesma velocidade.
d) As ondas possuem o mesmo comprimento de onda.
e) Os pontos P e Q da onda A vibram em concordância de fase.
Como as cordas são idênticas:
3. (FMJU-2013) – O forno de micro-ondas atua em uma frequência
de aproximadamente 2 GHz e transporta energia que é absorvida pelas
moléculas de água, de gordura e de açúcar, que apresentam polaridade.
Essas moléculas passam a vibrar, alinhando-se com a frequência das
ondas que incidem sobre elas, ocasionando o fenômeno da ressonância,
efeito no qual se baseia o aquecimento pelo forno de micro-ondas.
Apenas moléculas de água, gordura e açúcar entram em ressonância
com as micro-ondas. Essa é a vantagem de um aquecimento sob esse
processo, uma vez que as ondas só fazem ressonância com os alimentos
e não com os recipientes que os contêm. O ar de dentro do forno e os
recipientes se aquecem apenas por condução ou convecção através do
alimento aquecido.
a) Sabendo-se que a velocidade das micro-ondas é de 3 . 108m/s,
calcule o seu comprimento de onda.
b) Explique o que é aquecimento por condução e por convecção.
2
VB = VA ⇒ 12 fB = 8 fA ⇒ fB = ––– fA
3
RESOLUÇÃO:
a) V = f ⇒ 3 . 108 = 2 . 109
RESOLUÇÃO:
a) Onda A: AA = 2 unidades
Onda B: AB = 3 unidades
b) Onda A: A = 8 unidades
VA = A fA ⇒ VA = 8 fA
Onda B: B = 12 unidades
VB = B fB ⇒ VB = 12 fB
c) Os pontos P e Q, indicados na corda A, vibram em oposição de fase.
Resposta: C
2. (PUC-SP-2013) – Considere uma corda longa e homogênea, com
uma de suas extremidades fixa e a outra livre. Na extremidade livre da
corda é produzido um pulso ondulatório senoidal transversal que se
propaga por toda a sua extensão. A onda possui um período de 0,05s e
comprimento de onda 0,2m.
Da qual: = 0,15m = 15cm
b) Condução: Transmissão da energia térmica de molécula para molécula
de um meio material. A vibração de uma dada molécula é transmitida
à molécula vizinha e assim sucessivamente.
Convecção: Massas fluidas (líquidas ou gasosas) alternam posição
devido a diferença de densidades, deslocando, dessa maneira, a energia
térmica.
Respostas: a) 15cm
b) Ver textos
– 65
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 66
FRENTE 3 – ELETRICIDADE
MÓDULO 19
CAMPO MAGNÉTICO DO
CONDUTOR RETILÍNEO E DA ESPIRA
1. (ITA) – Assinale em qual das situações descritas nas opções
abaixo as linhas de campo magnético formam circunferências no
espaço.
a) Na região externa de um toroide.
b) Na região interna de um solenoide.
c) Próximo a um íma com formato esférico.
d) Ao redor de um fio retilíneo percorrido por corrente elétrica.
e) Na região interna de uma espira circular percorrida por corrente
elétrica.
RESOLUÇÃO
Olhando o fio de cima para baixo, vemos a corrente saindo do papel.
RESOLUÇÃO:
As linhas de campo magnético formam circunferências no espaço ao redor
de um fio retilíneo infinito percorrido por corrente elétrica.
→
A agulha magnética fica alinhada com o vetor indução magnética B.
Resposta: D
2. (MACK-2013) – Certo condutor elétrico cilíndrico encontra-se
disposto verticalmente em uma região do espaço, percorrido por uma
intensidade de corrente elétrica i, conforme mostra a figura abaixo.
Próximo a esse condutor, encontra-se a agulha imantada de uma
bússola, disposta horizontalmente. Observando-se a situação, acima
do plano horizontal da figura, segundo a vertical descendente, assinale
qual é o esquema que melhor ilustra a posição correta da agulha.
66 –
Resposta: A
Observação: Desprezou-se, nesse caso, a interferência do campo magnético
da Terra.
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 67
3. (FATEC-SP) – Dois fios metálicos retos, paralelos e longos, são
percorridos por correntes i e 3i de sentidos iguais (entrando no papel,
no esquema). O ambiente é vácuo. O campo magnético resultante,
produzido por essas correntes, é nulo em um ponto P tal que:
y
a) ––– = 3
x
y
1
b) ––– = –––
x
3
y
c) ––– = 9
x
y
1
d) ––– = –––
x
9
RESOLUÇÃO:
→
Usando a regra da mão direita sobre cada fio, determinamos os vetores B 1
→
e B 2 dos campos magnéticos gerados pelos fios da esquerda e da direita,
respectivamente.
MÓDULO 20
INDUÇÃO ELETROMAGNÉTICA
1. (FUVEST) – Aproxima-se um ímã de um anel metálico fixo em
um suporte isolante, como mostra a figura.
μ.i
Sendo B = –––––– , teremos:
2πd
μ.i
μ . (3i)
B1 = –––––– e B2 = –––––––
2πx
2πy
Fazendo-se B1 = B2 :
μ.i
3μ . i
1
3
–––––– = –––––– ⇒ ––– = –––
2πx
2πy
x
y
y
––– = 3
x
Resposta: A
4. (MODELO ENEM) – Indicar o sentido do campo magnético e a
polaridade magnética em cada um dos anéis e nos extremos do
solenoide das figuras 1, 2 e 3. O sentido da corrente elétrica está na
própria figura.
RESOLUÇÃO:
Usando a regra da mão direita, determinamos o sentido do campo mag→
nético B em cada elemento.
A polaridade magnética tem a seguinte resolução:
Anel 1: corrente no sentido anti-horário gera um polo norte.
Anel 2: corrente no sentido horário gera um polo sul.
Solenoide: visto pelo seu lado externo, vale: onde nasce o campo é o norte
e onde ele morre é o sul.
O movimento do ímã, em direção ao anel,
a) não causa efeitos no anel.
b) produz corrente alternada no anel.
c) faz com que o polo sul do ímã vire polo norte e vice-versa.
d) produz corrente elétrica no anel, causando uma força de atração
entre anel e ímã.
e) produz corrente elétrica no anel, causando uma força de repulsão
entre anel e ímã.
RESOLUÇÃO:
Quando o ímã é aproximado do anel, ocorre indução eletromagnética e
surge no anel uma corrente elétrica induzida (Lei de Faraday).
De acordo com a Lei de Lenz, surge uma força magnética de repulsão, isto
é, opondo-se ao movimento do ímã.
A figura ilustra a corrente induzida e a polaridade magnética no anel.
A corrente induzida não vai mudar de sentido, pois o ímã somente foi
aproximado do anel. Para se gerar uma corrente alternada, deveríamos
produzir no ímã um movimento de vai e vem, como, por exemplo, um MHS.
Resposta: E
– 67
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 68
2. (MODELO ENEM) – Na figura, mostra-se um experimento de
indução eletromagnética: um ímã, na mão de um operador, é aproximado de uma espira fixa, acendendo uma pequena lâmpada de LED.
A finalidade, no entanto é verificar a Lei de Lenz.
Em cada experimento:
a) Identifique se ocorrerá atração ou repulsão entre a espira e o ímã.
A seguir, identifique o polo magnético formado na espira, visto pelo
operador durante sua aproximação.
b) Indique o sentido da corrente elétrica, vista pelo operador.
c) Se, porventura, o operador voltar de costas, afastando o ímã da
espira, sem contudo invertê-lo, como será a força entre o ímã e a
espira?
RESOLUÇÃO:
a) Em ambos os experimentos, o ímã está sendo empurrado, pelo operador, contra a espira. Consequentemente, a Lei de Lenz nos assegura
que a força magnética decorrente da corrente induzida é de repulsão
ao movimento do ímã.
b) No experimento 1: a espira deverá repelir o polo sul do ímã aproximado
e, portanto, deverá tornar-se um polo sul; em consequência, a corrente
induzida, vista pelo operador, tem sentido horário.
No experimento 2:
A espira deverá repelir o polo norte do ímã aproximado e, portanto,
deverá tornar-se um polo norte; em consequência, a corrente elétrica
induzida, vista pelo operador, tem sentido anti-horário.
c) Haverá inversão do sentido das correntes em ambos os experimentos.
Experimento 1: passa a ter o sentido anti-horário.
Experimento 2: passa a ter o sentido horário.
Veja bem!
Poderíamos determinar o sentido da corrente induzida sem pensar na
força magnética, mas sim no aumento do fluxo induzido durante a
aproximação do ímã e na sua diminuição durante o afastamento. A
seguir, usamos a Lei de Lenz compensando a variação do fluxo e a regra
da mão direita.
3. (UEL) – Em uma usina hidroelétrica, a água do reservatório é
guiada através de um duto para girar o eixo de uma turbina. O
movimento mecânico do eixo, no interior da estrutura do gerador,
transforma a energia mecânica em energia elétrica que chega até nossas
casas. Com base nessas informações e em conhecimentos sobre o tema,
é correto afirmar que a produção de energia elétrica em uma usina
hidroelétrica está relacionada
a) à indução de Faraday.
b) à força de Coulomb.
c) ao efeito Joule.
d) ao princípio de Arquimedes.
e) ao ciclo de Carnot.
RESOLUÇÃO:
Nas usinas hidroelétricas, o eixo do gerador e o eixo da turbina são verticais
Eles são acoplados um ao outro com a turbina embaixo e o gerador em
cima.
68 –
Resposta: A
(MODELO ENEM) – Texto para as questões 4 e 5.
Numa usina eólica, um “catavento” gira com o fluxo eólico. Nesse
processo, adquire energia mecânica, a qual transmite para um gerador
elétrico. A figura ilustra um processo de transmissão mecânica.
4. Admitindo que a potência de um catavento seja de 10kW, que na
transmissão mecânica o rendimento seja de 90% e que no processo de
conversão de energia mecânica em elétrica haja uma perda de 3%, a
potência elétrica gerada será:
a) 10kW
b) 9,0kW
c) 8,73kW
d) 8,73kW
e) 80kW
RESOLUÇÃO:
O rendimento no processo de conversão de energia mecânica em elétrica é
97%. O rendimento total do processo é dado pelo produto dos dois
rendimentos:
η = 0,90 . 0,97 = 0,873
A potência elétrica gerada será:
Pel = 0,873 . 10(kW)
Pel = 8,73 kW
Resposta: C
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 69
5. Na geração eólica, o processo de conversão da energia mecânica
em elétrica no interior do gerador obedece à
a) Lei de Faraday.
b) Lei de Joule.
c) Lei de Coulomb.
d) lei da inércia.
e) Lei de Ohm-Pouillet.
2. Milikan descobriu com seu experimento que a carga elétrica é
quantizada e, em decorrência disso, escreve-se Q = n . e, sendo n um
valor inteiro.
RESOLUÇÃO:
A Lei de Faraday explica o processo de conversão de energia mecânica em
elétrica.
Resposta: A
MÓDULO 21
ELETROSTÁTICA:
ELETRIZAÇÃO POR ATRITO, CONTATO E INDUÇÃO
Determine a carga elétrica, em coulombs, de cada uma das esferas acima. Dado e = 1,6 . 10–19C.
RESOLUÇÃO:
1. Dispomos de quatro pequenas esferas metálicas, A, B, C e D. A
primeira delas possui uma carga elétrica de +64 pC e a quarta, uma
carga elétrica de –8 pC. As demais estão neutras. Determine a carga
elétrica em cada esferinha nos contatos que se propõem:
a)
b)
c)
d)
da esferinha A com a B;
da esferinha A com a C, após o contato anterior;
da esferinha B com a D, após os contatos anteriores;
das quatro esferinhas simultaneamente.
RESOLUÇÃO:
a) Contato entre A e B
+64pC + 0
–––––––––– = +32 pC (para cada uma delas)
2
b) Contato entre A e C, após o contato anterior:
+32pC + 0
–––––––––– = +16 pC (para cada uma delas)
2
c) Contato de B com D após os contatos anteriores
+32pC – 8pC
+24pC
–––––––––––– = ––––––– = +12 pC
2
2
d) Juntando as quatro esferinhas:
QA + QB + QC + QD = 4Q
+16pC + 12pC + 16pC + 12pC = 4Q
+56pC = 4Q ⇒ Q = 14pC
Cada esferinha ficará com 14 pC
Observação: devido ao princípio da conservação da carga elétrica, se
somarmos as cargas iniciais, o resultado deverá ser o mesmo:
+64pC + 0 + 0 –8pC = 4Q
⇒
+56pC = 4Q ⇒ Q = 14pC
– 69
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 70
3. (UERJ) – Três pequenas esferas metálicas, E1, E2 e E3,
eletricamente carregadas e isoladas, estão alinhadas, em posições fixas,
sendo E2 equidistante de E1 e E3. Seus raios possuem o mesmo valor,
que é muito menor que as distâncias entre elas, como mostra a figura:
4. Desenhe as cargas elétricas induzidas na esfera neutra. Considere
o bastão como corpo indutor.
As cargas elétricas das esferas têm, respectivamente, os seguintes
valores:
Q1 = +20μC
Q2 = –4μC
Q3 = –1μC
a) Admita que, em um determinado instante, E1 e E2 são conectadas
por um fio metálico; após alguns segundos, a conexão é desfeita.
Nessa nova configuração, determine as cargas elétricas de E1 e E2.
b) Admita que os três foram conectados por fios, Como fica a nova
distribuição de cargas?
RESOLUÇÃO:
a)
RESOLUÇÃO:
Q1 + Q2
–16μC
(+20) + (–4)
Q’1 = Q’2 = ––––––––
= –––––––––– μC = –––––––
2
2
2
Q’1 = Q’2 = +8μC
b)
∑Q
+15μC
(+20) + (–4) + (–1)
Q final = –––– = ––––––––––––––––– μC = –––––––
3
3
3
Q final = +5μC
70 –
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 71
MÓDULO 22
FORÇA ELETROSTÁTICA
1. Duas partículas, A e B, estão fixas numa mesa de laboratório, a
uma distância de 2,0cm uma da outra. O meio é o ar, para o qual a
constante eletrostática é K= 9,0 x 109 N.m2/C2.
Suas cargas elétricas são, respectivamente: 4,0 . 10–4 C e 8,0 . 10–9 C.
Determine a intensidade da força elétrica entre as duas partículas.
3. (UFTM) – O gráfico mostra como varia a força de repulsão entre
duas cargas elétricas, idênticas e puntiformes, em função da distância
entre elas.
RESOLUÇÃO:
A intensidade da força elétrica é dada pela Lei de Coulomb. Devemos
converter a unidade de distância para metro.
2,0 cm = 2,0 . 10–2 m
9,0 . 109 . 4,0 . 10–4 . 8,0 . 10–9
K . QA . QB
F = –––––––––– ⇒ F = –––––––––––––––––––––––––– (N) ⇒ F = 72N
(2,0 . 10–2)2
d2
Resposta: 72N
Considerando a constante eletrostática do meio como k = 9 . 109N . m2/C2,
determine
a) a intensidade da força F2.
b) o módulo das cargas elétricas.
2. (VUNESP) – Considere duas pequenas esferas eletrizadas,
separadas pela distância d = 3,0 . 10–1m, em que uma delas possui carga
elétrica Q1 = 1,0nC e a outra, Q2 = –5,0nC. Utilizando-se a constante
eletrostática K0 = 9,0 . 109N · m2 /C2,
a) calcule o módulo da força eletrostática entre elas.
b) determine novamente o módulo da força eletrostática, porém para
uma nova distância D = 6,0 . 10–1m (o dobro da anterior).
RESOLUÇÃO:
a) Lei de Coulomb:
RESOLUÇÃO:
a) Para uma distância di temos uma força de intensidade Fi
d1 = 0,1m ⇒ F1 = 9,0 . 103N
1
d2 = 0,3m = 3d1 ⇒ F2 = –– F1
9
F2 = 1,0 . 103N
Q2
d21 . F1
(0,1)2 . 9,0 . 103
b) F1 = k . –––
⇒ Q2 = ––––––
= ––––––––––––––
(unid. SI)
2
d1
9
9,0 . 109
Q2 = 1,0 . 10–8 (unid. SI) ⇒
Q = 1,0 . 10–4C
Q1 . |Q2 |
9,0 . 109 . 1,0 . 10–9 . 5,0 . 10–9
F = K0 . ––––––––– ⇒ F = ––––––––––––––––––––––––––– (N)
(3,0) 2 . (10–1) 2
d2
F = 5,0 . 10–7N
Q1 . |Q2 |
Q1 . |Q2 |
b) F’ = K0 ––––––––– = K0 ––––––––– =
D2
(2d)2
F
F’ = ––– ⇒
4
1
Q1 . |Q2 |
––– . K0 –––––––––
4
d2
F’ = 1,25 . 10–7N
– 71
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 72
4. (MODELO ENEM) – Duas partículas de cargas elétrica Q e q
estão fixas a uma distância d uma da outra, num ambiente em que foi
feito vácuo (fig. 1). Nesse mesmo ambiente, outras duas partículas de
cargas 2Q e 5q estão fixas a uma distância 2d uma da outra.
Ao transferirmos metade da carga de uma delas para a outra, teremos: Q/2
e 3Q/2 e a nova força F’ terá intensidade:
3Q2
Q
3Q
–––
––––
––––
2
2
4
3
F’ = K –––––––––––––– = K ––––––––––– = ––– .
2
2
4
d
d
Logo F’ = F ou F = F’
Sendo F1 a intensidade da força entre as duas primeiras (fig. 1) e sendo
F2 a intensidade da força entre as duas últimas (fig. 2), a relação entre
F1 e F2 é:
a) F1 = F2
5
b) F1 = –– F2
2
d) F1 = 5F2
e) F1 = F2/5
Resposta: D
2
c) F1 = –– F2
5
MÓDULO 23
CAMPO ELÉTRICO
RESOLUÇÃO:
Q.q
F1 = K –––––
d2
2Q . 5q
5.2K.Q.q
5KqQ
= ––––––––
F2 = K ––––––––
= ––––––––––––
(2d)2
4d2
2d2
K.Q.q
––––––––
F1
2
d2
––– = –––––––––––– = –––
5 . K. q . Q
F2
5
––––––––––
2d2
1. Na figura temos um campo elétrico gerado por uma carga fonte Q
positiva e, nas suas imediações há um ponto geométrico P, no qual o
→
vetor campo elétrico é E (não desenhado).
→
a) Desenhe, em P o vetor campo elétrico E.
b) Um operador transporta até P uma carga de prova q < 0, puntiforme.
→
Represente essa carga em P e desenhe a força elétrica F.
→
c) Determine o módulo de F em função de q e de E.
→
d) Determine o módulo de F em função de q, Q, d e k(constante
eletrostática.
2
F1 = ––– F2
5
Resposta: C
RESOLUÇÃO:
a)
5. Duas pequenas esferas estão eletrizadas com cargas elétricas idênticas, iguais a Q. Estando separadas por uma distância d, a força de
repulsão entre elas tem intensidade F. Retiramos metade da carga
elétrica de uma delas e transferimos para a outra, sem contudo tirarmos
as esferas do seu lugar. A nova força de repulsão entre elas terá módulo
F’, tal que:
a) F = F’
b) F’ = 2F
c) F = 2F’
d) F’ = 3F/4
e) F = 3F’/4
RESOLUÇÃO:
Inicialmente, tínhamos:
Q. Q
Q2
F = K –––––– = K ––––
d2
d2
72 –
b)
c) F = q . E
Q
q.Q
d) E = k –––
⇒ F = k . ––––––– (Lei de Coulomb)
d2
d2
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 73
2. (UECS-AL-VUNESP-MODELO ENEM) – A figura representa
a intensidade do campo elétrico criado por uma carga puntiforme Q,
em função da distância d à carga.
3. (UPF) – Uma pequena esfera de 1,6g de massa é eletrizada
retirando-se um número n de elétrons. Dessa forma, quando a esfera é
colocada em um campo elétrico uniforme de 1,0 . 109N/C, na direção
vertical para cima, a esfera fica flutuando no ar em equilíbrio.
Considerando que a aceleração gravitacional local g é 10m/s2 e a carga
de um elétron é 1,6 . 10–19C, pode-se afirmar que o número de elétrons
retirados da esfera é:
a) 1,0 . 1019
b) 1,0 . 1010
c) 1,0 . 109
d) 1,0 . 108
e) 1,0 . 107
A intensidade da força elétrica que agirá sobre uma carga de prova
q = 2,0 C, colocada a 0,3m de Q, valerá, em N,
a) 2,0 . 10–3
b) 2,0 . 10–2
c) 2,0 . 10–1
d) 1,0 . 10–2
e) 1,0 . 10–1
RESOLUÇÃO:
A intensidade do campo elétrico é inversamente proporcional ao quadrado da distância entre a carga fonte e o ponto P. Triplicamos a distância e
temos:
E1
4,5 . 105
E2 = ––– ⇒ E2 = –––––––– N/C = 0,5 . 105 N/C
d2
9
A carga de prova é colocada nesse ponto P.
F = q E2 = 2,0 . 10–6 . 0,5 . 105 (N)
F = 1,0 . 10–1N
RESOLUÇÃO:
→
Devido à gravidade, age na esfera uma força gravitacional (peso) P e devido
→
ao campo elétrico age na esfera a força elétrica F.
F=q.E
q=n.e
F=n.eE
P=m.g
Mas, no equilíbrio:
n.e.E=m.g
m.g
(1,6 . 10–3) . 10
n = –––– ⇒ n = –––––––––––––––––––
(1,6
. 10–19) . (1,0 . 109)
e.E
Resposta: E
n = 1,0 . 108 elétrons
Resposta: D
– 73
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 74
MÓDULO 24
2. (MACKENZIE-2013) – Fixam-se as cargas puntiformes q1 e q2,
de mesmo sinal, nos pontos A e B, ilustrados acima.
CAMPO ELÉTRICO RESULTANTE
1. Nas figuras de 1 a 3 estão representadas configurações formadas
por duas cargas elétricas puntiformes Q1 e Q2 que são as fontes de um
campo elétrico no ponto P. Represente, em cada situação, o vetor
→
campo elétrico E1, gerado por Q1 em P e E2 gerado por Q2 em P.
Para que no ponto C o vetor campo elétrico seja nulo, é necessário que
1
1
a) q2 = ––– q1
b) q2 = ––– q1
3
9
c) q2 = 3 q1
e) q2 = 9 q1
RESOLUÇÃO:
Para q1 e q2 positivas, temos:
E1 = E2
k q1
k q2
––––– = –––––
d2
9 d2
RESOLUÇÃO:
q2 = 9 q1
Resposta: E
Para as três figuras, valem as seguintes propriedades:
→
Q > 0 ⇒ E (afastamento)
→
Q < 0 ⇒ E (aproximação)
74 –
d) q2 = 6 q1
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 75
3. (UFPE) – Uma carga elétrica puntiforme gera campo elétrico nos
pontos P1 e P2. A figura a seguir mostra setas que indicam a direção e
o sentido do vetor campo elétrico nestes pontos. Contudo, os
comprimentos das setas não indicam os módulos destes vetores. O
módulo do campo elétrico no ponto P1 e 32 V/m. Calcule o módulo do
campo elétrico no ponto P2, em V/m.
4. (FCC) – Na figura, estão representadas quatro cargas elétricas de
mesmo módulo, duas positivas e duas negativas, fixadas nos vértices
de um quadrado.
O vetor campo elétrico resultante desta configuração de cargas, no
centro do quadrado, é representado por
→
→
→
→
→ →
a) E1
b) E2
c) E3
d) E4
e) E = 0
RESOLUÇÃO:
RESOLUÇÃO:
Observe a simetria das cargas em cada diagonal. Isso nos leva a campo
→
resultante nulo no centro do quadrado. Logo, Eres = 0.
Resposta: E
Inicialmente, temos de localizar a carga elétrica fonte: Q. Para tanto traça→
→
mos as retas suportes dos vetores E1 e E2. No encontro teremos a carga Q.
d2 = 4u (4 unidades de comprimento)
d1 = 2 2 u (hipotenusa)
Q
K.Q
E2 = k . ––––– = –––––
(4u)2
16u2
Q
K.Q
E1 = k . ––––––––– = –––––
8 . u2
(2
2 u)2
1
–––
16
8
1
E1
E2
32
= ––– (V/m)
––– = ––––– = ––– = ––– ⇒ E2 = –––
1
16
2
E1
2
2
–––
8
E2 = 16V/m
– 75
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 76
FRENTE 1
MÓDULO 19
4. (FATEC) – Um corpo A de massa 1,0kg está preso a um balde B
de massa 200g, por um fio inextensível de massa desprezível. Joga-se
nesse balde, com uma jarra J, uma certa quantidade de água.
ATRITO
1. Considere um bloco de massa 2,0kg em um plano horizontal, inicialmente em repouso. Uma força horizontal constante de intensidade
F é aplicada ao bloco.
Os coeficientes de atrito estático e dinâmico entre o bloco e o plano
valem, respectivamente, 0,50 e 0,40. Adote g = 10,0m/s2.
Calcule a intensidade da força de atrito entre o plano e o bloco e o
módulo da aceleração do bloco, nos seguintes casos:
a) F = 9,0N
b) F = 12,0N
Sendo g = 10m/s2 e o coeficiente de atrito estático entre o corpo A e a
superfície de apoio = 0,30, a máxima quantidade de água que se pode
colocar no balde para que o sistema permaneça em equilíbrio é de:
a) 500g
b) 400g
c) 300g
d) 200g
e) 100g
5. Dois móveis, M e N, ligados por uma corda de peso desprezível,
deslocam-se sobre um plano horizontal, sob a ação de uma força de
intensidade 15,0 newtons aplicada na direção do deslocamento.
2. (PUC-PR) – Um rapaz puxa um caixote de 40 kg com uma força
horizontal constante, de intensidade 200N. O caixote move-se com
velocidade constante sobre uma superfície horizontal. Calcule o coeficiente de atrito dinâmico entre a superfície e o caixote Adote
g = 10m/s2 e despreze o efeito do ar.
Desprezando-se o atrito entre o corpo M e o plano e admitindo-se que
o coeficiente de atrito de escorregamento entre o corpo N e o plano
vale 0,20 e que as massas de M e N são, respectivamente, 1,0kg e
3,0kg, pedem-se:
a) o módulo da aceleração do sistema;
b) a intensidade da força tensora no fio.
Considere g = 10m/s2 e despreze o efeito do ar.
3. (UFC) – O bloco, da figura abaixo, tem massa M = 10kg e repousa sobre uma superfície horizontal. Os coeficientes de atrito estático e
cinético, entre o bloco e a superfície, são E = 0,40 e C = 0,30, respectivamente. Aplicando-se ao bloco uma força horizontal constante de
intensidade F = 20N, determine a intensidade da força de atrito que
atua sobre ele.
(Considere g = 10m/s2 e despreze o efeito do ar.)
76 –
6. (AMAN) – Na figura abaixo, a superfície é horizontal, a roldana
e o fio empregados têm massas desprezíveis e existe atrito apenas entre
os blocos e a superfície de apoio. Despreze o efeito do ar.
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 77
Sendo g = 10m.s–2 e o coeficiente de atrito cinético igual a 0,20,
pedem-se:
a) o módulo da aceleração dos blocos;
b) a intensidade da força tensora no fio;
c) a intensidade da força de contato entre A e B.
Dados: mA = 20kg;
mB = 10kg;
mC = 10kg.
Dados: sen 37° = cos 53° = 0,60
cos 37° = sen 53° = 0,80
g = 10m/s2
MÓDULO 20
PLANO INCLINADO
1. Considere um plano inclinado que forma um ângulo com o
plano horizontal. Despreze o efeito do ar.
a) Determine a intensidade da aceleração adquirida pelo bloco.
b) Calcule a distância percorrida pelo bloco após decorrido um tempo
de 2,0s.
→
4. (FATEC) – Uma força F paralela ao plano inclinado de ângulo com a horizontal é aplicada ao corpo de massa 10kg, para que ele suba
o plano com aceleração de módulo igual a 2,0m/s2 e dirigida para cima.
Sendo sen = 0,60, cos = 0,80 e g = 10 m.s–2, calcule
a) a intensidade da aceleração de um corpo que escorrega livremente
neste plano, sem atrito;
b) o coeficiente de atrito dinâmico entre um corpo e o plano, para que
o corpo lançado para baixo desça o plano com velocidade constante.
2. (PUC) – Um bloco de 5,0kg de massa está em repouso sobre um
plano inclinado.
Considerando-se desprezível o atrito, adotando-se para o módulo de g
→
o valor de 10m/s2, cos = 0,60 e sen = 0,80, o módulo de F vale:
a) 120N
b) 100N
c) 80N
d) 60N
e) 20N
5. (FATEC) – Um bloco de 40kg está apoiado sobre um plano incli→
nado de 30° e sobe, a partir do repouso, sob ação da força F paralela
ao plano inclinado, com aceleração escalar de 2,0m/s2. O coeficiente
de atrito cinético entre o bloco e o plano vale 0,40.
é o ângulo de inclinação do plano.
a) O que acontece com o módulo da força de reação normal do plano,
na medida em que aumenta de valor?
b) Qual o módulo da aceleração do bloco, quando o ângulo de inclinação do plano for igual a 18°?
Dados:
1) sen 18° 0,30; cos 18° 0,95
2) módulo da aceleração da gravidade local: g = 10m/s2
3) módulo da força de atrito: fat = 5,0N
3. (MED.VIÇOSA) – Um bloco de 3,0kg é abandonado com velocidade inicial V0 = 0 sobre um plano inclinado de 37° com a horizontal,
como mostra a figura abaixo. O coeficiente de atrito entre o bloco e o
plano inclinado é 0,50. Despreze o atrito com o ar.
Adotando-se g = 10m/s2, o valor de F é, aproximadamente:
a) 419N
b) 280N
c) 200N
d) 180N
e) 100N
– 77
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 78
MÓDULO 21
COMPONENTES DA RESULTANTE
1. (UFPE) – Um automóvel de massa igual a 1,0t descreve uma curva circular de raio 100m com velocidade escalar constante de 10m/s,
em um plano horizontal.
Qual a intensidade da força de atrito entre os pneus e a estrada para
evitar que o carro derrape?
2. (CESGRANRIO) – A partir de um ponto muito próximo da superfície terrestre, na região polar, uma pedra é atirada horizontalmente
e se transforma em um satélite artificial da Terra em órbita circular.
Admitindo-se a Terra rigorosamente esférica de raio 6,4 . 106m, desprezando-se a influência da atmosfera terrestre e adotando-se g = 10m/s2,
calcule a intensidade da velocidade de lançamento da pedra.
a) Qual a intensidade da força resultante sobre o carro enquanto estiver
na ponte?
b) Qual a intensidade da força com que o carro pressiona a ponte ao
passar pelo seu ponto mais alto?
5. (FATEC) – Um motociclista move-se no interior de um globo
metálico de raio R = 1,5m. Num determinado instante, ele passa pelo
ponto mais alto da trajetória. Qual deve ser a velocidade mínima, neste
instante, para que a moto não perca o contato com a superfície do
globo? Adote g = 10m.s–2.
MÓDULO 22
EXERCÍCIOS DE FORÇA CENTRÍPETA
3. No esquema, temos um pêndulo simples de comprimento L e com
uma esfera de massa m, oscilando entre os pontos A e B.
1. (UNIFICADO-RJ) – Um soldado em treinamento utiliza uma
corda de 5,0m para “voar” de um ponto a outro como um pêndulo simples. Se a massa do soldado é de 80 kg, a corda sendo ideal, e a sua
velocidade escalar no ponto mais baixo de 10m/s, desprezando-se todas
as forças de resistência, a razão entre as intensidades da força que o
soldado exerce no fio e de seu peso é: (g = 10m/s2)
a) 1/3
b) 1/2
c) 1
d) 2
e) 3
2. Considere um trilho circular de raio R = 2,0m, sem atrito e colocado em posição vertical e fixo no solo. Um bloco de massa 3,0kg
desliza no trilho e atinge o ponto mais baixo (A) com velocidade de
módulo igual a 4,0m/s.
A velocidade escalar da esfera ao passar pelo ponto M vale V.
A intensidade da força que traciona o fio ao passar pelo ponto M será
igual a:
mV2
a) zero
b) mg
c) mg – –––––
L
mV2
mV2
d) mg + –––––
e) –––––
L
L
Nota: g = módulo da aceleração da gravidade local.
Calcule
a) a intensidade da força centrípeta no ponto mais baixo (A);
b) a intensidade da força que o trilho exerce sobre o bloco no ponto mais
baixo (A), adotando-se g = 10m/s2.
4. (UFSC) – Um carro de massa m = 1,6 . 103 kg passa por uma ponte convexa com velocidade escalar constante V = 36km/h. O raio da
ponte, suposta com perfil circular, é R = 80m. Adote g = 10,0m/s2 e
despreze o efeito do ar.
3. Em um parque de diversões, há uma roda gigante de raio 24m,
que gira com velocidade angular constante.
A cadeira é articulada de forma que a pessoa se mantenha sempre
sentada na posição normal.
78 –
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 79
Quando passa pelo ponto mais baixo da trajetória, a pessoa exerce
sobre a cadeira uma força de intensidade 610N e quando passa pelo
ponto mais alto, a intensidade é de 590N.
Sendo g = 10m.s–2, calcule
a) a massa da pessoa;
b) a velocidade escalar da pessoa.
4. Um automóvel, em movimento uniforme, entra numa curva circular de raio R, contida em um plano horizontal.
Sendo g o módulo da aceleração da gravidade, determine a máxima
velocidade possível na curva, sem que o carro derrape. O coeficiente de
atrito entre os pneus e o chão é constante e vale .
5. (UFCE) – Um veículo de peso P = 1,6 . 104N percorre um trecho
de estrada em lombada, com velocidade escalar constante de 72km/h.
A intensidade da força normal, que o leito da estrada exerce no veículo
quando ele passa no ponto mais alto da lombada, é de 8,0 . 103N. Parte
da lombada confunde-se com um setor circular de raio R, como mostra
a figura. Usando-se g = 10m/s2, determine, em metros, o valor de R.
MÓDULO 23
TRABALHO
1. Um bloco de peso 10N está em movimento sobre um plano horizontal, no sentido da esquerda para a direita. No esquema, estão
representadas as forças que atuam no bloco.
Para um percurso de 2,0m, o trabalho
→
a) da força de atrito ( Fat ) é igual a 120 J;
→
b) do peso ( P ) é igual a 200J;
→
c) da força ( F ) é igual a 680J;
→
d) da força de reação normal do apoio ( R ) é igual a 160J;
e) da força resultante é igual 40J.
3. (UNIRIO) – Três corpos idênticos, de massa M, deslocam-se
entre dois níveis, como mostra a figura: A – caindo livremente; B –
deslizando ao longo de um tobogã e C – descendo uma rampa, sendo,
em todos os movimentos, desprezíveis as forças dissipativas.
Com relação ao trabalho (W) realizado pela força peso dos corpos,
pode-se afirmar que:
a) WC > WB > WA
b) WC > WB = WA
c) WC = WB > WA
d) WC = WB = WA
e) WC < WB > WA
4. Considere um satélite artificial de massa m em órbita circular de
raio R em torno da Terra, com velocidade escalar V.
O trabalho da força gravitacional que a Terra aplica no satélite
a) é sempre nulo, pois a força gravitacional é centrípeta;
b) somente é nulo para uma volta completa do satélite;
m V2
c) vale –––––– . 2πR;
2
m V2
d) vale –––––– ;
2
→
→
São dados | F1 | = 10,0N; | F2 | = 2,0N.
Calcule o trabalho que cada uma das forças realiza em um deslocamento de 5,0m.
2. (FUND. CARLOS CHAGAS) – Um corpo de peso P = 100N
é puxado sobre um plano horizontal por uma força horizontal constante
e de intensidade F = 80N. A força de atrito que o plano exerce sobre o
bloco é constante e de intensidade Fat = 60N.
m V2
e) vale –––––– .
R
5. (FUVEST) – Um objeto de 20kg desloca-se numa trajetória
retilínea de acordo com a equação horária dos espaços:
s = 10,0 + 3,0t + 1,0t2
em que s é medido em metros e t em segundos.
a) Qual a expressão da velocidade escalar do objeto no instante t?
b) Calcule o trabalho realizado pela força resultante que atua sobre o
objeto durante um deslocamento de 20m.
– 79
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 80
MÓDULO 24
TEOREMA DA ENERGIA
CINÉTICA E MÉTODO GRÁFICO
1. (FUVEST) – O gráfico velocidade escalar versus tempo,
mostrado adiante, representa o movimento retilíneo de um carro de
massa m = 6,0 . 102kg em uma estrada molhada. No instante t = 6,0s
o motorista vê um engarrafamento à sua frente e pisa no freio. O carro, então, com as rodas travadas, desliza na pista até parar completamente. Despreze a resistência do ar e adote g = 10m/s2.
a) 6 5N
b) 20N
c) 27N
d) 36N
e) 45N
4. (FEI) – Uma partícula de massa 2,0kg desloca-se ao longo de um
→
eixo Ox, sob ação de uma força resultante F que tem a mesma
orientação do eixo Ox e intensidade variando com a posição, conforme o gráfico a seguir.
Sabe-se que na posição x1 = 0, a velocidade escalar da partícula é de
10
m/s:
a) Qual é o coeficiente de atrito entre os pneus do carro e a pista?
b) Qual o trabalho realizado pela força de atrito entre os instantes
t = 6,0s e t = 8,0s?
2.
Considere um cometa em órbita elíptica em torno do Sol.
Determine:
→
a) o trabalho realizado pela força F entre as posições x1 = 0 e
x2 = 3,0m;
b) a velocidade escalar da partícula na posição x2 = 3,0m.
Quando o cometa passa pelo afélio (ponto B), sua velocidade linear de
translação tem módulo V e sua energia cinética vale E.
Quando o cometa passa pelo periélio (ponto A), sua velocidade linear
de translação tem módulo 2V.
No trajeto de B para A, o trabalho da força gravitacional que o Sol
aplica no cometa vale:
a) 0
b) E
c) 2E
d) 3E
e) 4E
3. (FEI) – Utilizando uma pá, um servente de pedreiro atira um
tijolo verticalmente para cima. O tijolo tem massa 2,0kg e encontra-se,
inicialmente, em repouso sobre a pá no ponto O ao nível do solo. O
servente, usando a pá, acelera o tijolo uniformemente até o ponto P,
onde o tijolo abandona a pá e prossegue na trajetória vertical até Q,
onde chega com velocidade nula. Despreze o efeito do ar e adote
→
g = 10 m/s2. A força F aplicada pela pá sobre o tijolo, suposta constante,
tem intensidade igual a:
80 –
5. (UNICAMP) – Mostra-se, em função da distância x, a intensidade da força resultante F que atua sobre um corpo de massa
m = 1,2kg, que se desloca sobre uma trajetória retilínea.
a) Qual é o módulo da aceleração do corpo quando ele passa pela
posição x = 4,0m?
b) Sabendo-se que o corpo tinha velocidade nula em x = 0, qual é a
sua velocidade escalar na posição x = 4,0m?
6. Em um plano inclinado de 30°, um bloco de massa 2,0kg está
→
sendo empurrado para cima por uma força F, paralela ao plano
inclinado, e de intensidade variável com a distância do bloco ao ponto
A, segundo o gráfico apresentado adiante.
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 81
c) Reflexão total só pode ocorrer para luz propagando-se no meio (2).
d) Quando há refração, não há reflexão.
e) n.d.a.
2. (FUND. CARLOS CHAGAS) – Se o meio (1) é mais refringente
que o meio (2), sendo L o ângulo limite de reflexão total, dos gráficos
a seguir, o que não contradiz a Lei de Snell é:
O bloco parte do repouso em A, o atrito é desprezível, a aceleração da
gravidade local tem intensidade g = 10 m/s2 e o ponto B está a uma
altura H = 5,0 m.
Calcule
→
a) os trabalhos da força F e do peso do bloco, no deslocamento de A
para B;
b) a intensidade da velocidade do bloco ao atingir o ponto B.
FRENTE 2
Nota:
L = ângulo limite.
L < L’ sofre reflexão total.
MÓDULO 19
REFRAÇÃO (II) – REFLEXÃO TOTAL
3. (U.F.VIÇOSA) – A figura a seguir mostra uma cuba semicilíndrica transparente contendo água.
1. (FATEC) – O esquema anexo representa um pincel de luz monocromática que atravessa a superfície separadora de dois meios transparentes, (1) e (2).
a) A luz propaga-se necessariamente no sentido do meio (1) para o
meio (2).
b) O meio (1) é mais refringente do que o meio (2).
Três raios de luz monocromática, A, B e C, incidem na cuba, como
ilustrado na figura.
O(s) raio(s) que está(ão) traçado(s) erradamente é(são)
a) somente A.
b) A e B.
c) B e C.
d) somente B.
e) A e C.
– 81
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 82
4. (UFGO) – Um raio de luz monocromática incide com um ângulo de
2 ), conforme a figura:
45° na face lateral de um cubo de vidro (nv = a) Determine o ângulo de refração r.
b) Dizer o que acontecerá com o raio ao atingir a face superior do cubo
e construir a sequência do caminho óptico desse raio.
MÓDULO 20
LENTES ESFÉRICAS I – CONTRUÇÕES GRÁFICAS
4. Uma lente biconvexa, construída de material de índice de refração
absoluto nL, encontra-se imersa num meio de índice de refração
absoluto nM. Nessas condições, a lente será
a) convergente se nL < nM
b) divergente se nL > nM
c) divergente se nL < nM
5. (FUND. CARLOS CHAGAS) – Uma lente, feita de material cujo
índice de refração absoluto é 1,5, é convergente no ar. Quando mergulhada
num líquido transparente, cujo índice de refração absoluto é 1,7, ela
a) será convergente.
b) será divergente.
c) será convergente somente para a luz monocromática.
d) comportar-se-á como uma lâmina de faces paralelas.
e) não produzirá nenhum efeito sobre os raios luminosos.
6. (UNIP) – Assinale a opção que traduz o comportamento característico de uma lente convergente:
1. (PUC) – Deseja-se concentrar a luz do Sol num ponto, para se
obter um forno solar, usando-se apenas um dos elementos abaixo.
Indicar qual deles deve ser usado:
a) Espelho plano.
b) Lente convergente.
c) Lente divergente.
d) Espelho convexo.
e) Prisma.
2. (CESGRANRIO) – Um estudante deseja queimar uma folha de
papel, concentrando, com apenas uma lente, um feixe de luz solar na
superfície da folha.
Para tal, ele dispõe de 4 lentes de vidro, cujos perfis são mostrados abaixo.
Para conseguir seu intento, o estudante poderá usar as lentes
a) I ou II, somente.
b) I ou III, somente.
c) I ou IV, somente.
d) II ou III, somente.
e) II ou IV, somente.
3. (SOROCABA-SP) – Uma lente de vidro cujos bordos são mais
espessos que a parte central
a) deve ser divergente.
b) deve ser convergente.
c) no ar, é sempre divergente.
d) mergulhada num líquido, torna-se divergente.
82 –
7. (MED. ABC) – Uma pequena lâmpada é colocada sobre o eixo
principal de uma lente convergente de distância focal f e uma pessoa
observa sua imagem no outro lado da lente. A imagem observada é
menor que o objeto e é invertida. É mais correto dizer que a pessoa
observa uma imagem
a) que é real e situada a uma distância menor que 2f em relação à lente.
b) que é virtual, uma vez que não se projeta sobre um anteparo.
c) projetada no infinito.
d) que é real, estando o objeto a uma distância menor que 2f, em
relação à lente.
e) só quando projetada num anteparo.
8. (U.F. FLUMINENSE) – Quando uma lente plano-convexa, mergulhada no ar, produz uma imagem virtual de um objeto real, esta imagem é
a) menor do que o objeto e direita.
b) menor do que o objeto e invertida.
c) maior do que o objeto e invertida.
d) maior do que o objeto e direita.
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 83
9. (FUND. CARLOS CHAGAS) – Um objeto é colocado diante
de uma lente convergente cuja distância focal é f, num ponto entre f e
2f, com sua base sobre o eixo principal da lente. A imagem é, neste
caso,
a) real, invertida e de tamanho maior que o objeto.
b) real, invertida e de tamanho igual ao objeto.
c) virtual, direita e de tamanho maior que o objeto.
d) virtual, direita e de tamanho menor que o objeto.
e) virtual, invertida e de tamanho menor que o objeto.
a) Qual a posição da imagem?
b) Fazer o traçado dos raios.
3. (FUVEST) – Um objeto A está situado a 5,0cm de uma lente
convergente L1, cuja distância focal é 4,0cm. Uma segunda lente
convergente, idêntica à anterior, é colocada a 2,0cm de distância da
imagem A’. A figura ilustra o esquema.
10. (FUND. CARLOS CHAGAS) – A imagem de um objeto real,
conjugada por uma lente divergente, é sempre
a) virtual, direita e menor do que o objeto.
b) virtual, direita e maior do que o objeto.
c) real, invertida e menor do que o objeto.
d) real, direita e maior do que o objeto.
e) real, direita e menor do que o objeto.
11. Na figura a seguir, estão representados o eixo óptico (x) de uma
lente convergente, um objeto (O) e sua imagem (I), conjugada pela
lente. Aproximadamente, em que ponto do eixo óptico deve estar
localizada a lente?
a) A que distância de L1 se encontra L2?
b) Qual a amplificação do sistema L?
4. (UnB) – Um objeto real está localizado no eixo principal de uma
lente convergente, distante 20cm do seu centro. Sabendo que a distância
focal é de 10cm, calcule a distância da imagem ao objeto em cm.
5. (MACKENZIE) – Uma lente esférica produz uma imagem real
de mesmo tamanho do objeto, quando este está a 20cm dela. Para que
a imagem se forme no infinito, qual a distância entre o objeto e a lente?
MÓDULO 21
LENTES ESFÉRICAS II – ESTUDO ANALÍTICO
E VERGÊNCIA DE UMA LENTE
1. (PUC) – Uma lente convergente fornece, de um objeto real, disposto perpendicularmente ao seu eixo e situado a 3,0cm de distância,
uma imagem virtual três vezes maior do que o objeto. A distância focal
da lente é
a) 4,5cm b) 2,25cm c) 0,48cm d) 5,0cm
e) 3,0cm
2. (FUVEST) – Um objeto luminoso de 1,0cm de altura está a 5,0cm
de uma lente convergente de 10cm de distância focal (vide figura).
6. (FUND. CARLOS CHAGAS) – Uma esfera de 1,0cm de
diâmetro é observada com uma lente convergente. A imagem da esfera
tem 2,0cm de diâmetro, quando o centro da esfera-objeto está a 2,0cm
da lente. Qual é a distância focal da lente?
7.
(FNM) – Qual a distância focal de uma lente de vergência 4,0 di?
MÓDULO 22
ÓPTICA DA VISÃO
1. (MED. CATANDUVA) – Pessoas míopes possuem o globo
ocular longo. Para corrigir esse defeito da visão, usam-se geralmente
a) lentes convergentes.
b) lentes cilíndricas.
c) lentes divergentes.
d) prismas especiais.
2. Para o defeito de visão denominado miopia:
(1) a imagem de um objeto impróprio forma-se aquém da retina;
(2) a correção é feita com o uso de lentes divergentes;
(3) o ponto remoto está a uma distância finita;
(4) o ponto remoto é virtual.
Quais as proposições corretas?
– 83
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 84
3. (POUSO ALEGRE-MG) – A receita de óculos para míope indica
que ele deve usar “lentes de 2,0 graus”, isto é, o valor de convergência
das lentes deve ser – 2,0 dioptrias. O que podemos concluir sobre as
lentes desses óculos?
4. (FUND.CARLOS CHAGAS) – A lente do olho (cristalino) e as
lentes para corrigir os defeitos I e II são, respectivamente,
a) convergente, divergente e divergente;
b) divergente, convergente e divergente;
c) convergente, convergente e divergente;
d) divergente, divergente e convergente;
e) convergente, divergente e convergente.
5. (MED.ABC) – A distância normal de visão distinta é aproximadamente 25cm. Considere uma pessoa que não consegue ler um livro
quando este está a uma distância menor do que 100cm dos olhos. Se
desejar lê-lo, mantendo-o a 25cm de distância dos olhos, deve adquirir
óculos cujas lentes sejam
a) convergentes, de distância focal menor ou igual a 25cm;
b) convergentes, de distância focal entre 25cm e 100cm;
c) divergentes, de distância focal menor ou igual a 25cm;
d) divergentes, de distância focal entre 25cm e 100cm;
e) convergentes, de distância focal maior ou igual a 100cm.
MÓDULO 23
d) os estrondos referidos são, na realidade, decorrentes da explosão
de raios laser;
e) nenhuma alternativa anterior é correta.
3. (UNIFOR) – Como exemplos de propagação ondulatória, podem
ser citados(as)
a) a luz e o som.
b) a luz e o vento.
c) o som e o vento.
d) o som e a fumaça.
e) as inundações e as doenças.
4.
a)
b)
c)
d)
e)
(PUC) – Em relação às ondas luminosas, pode-se afirmar que
são longitudinais;
são transversais;
não se propagam no vácuo;
não podem ser polarizadas;
propagam-se no vácuo com velocidade 3.105 m/s.
5. (FUVEST) – Em qual dos fenômenos a seguir as ondas são
longitudinais?
a) luz de laser;
b) raios X;
c) raios gama;
d) vibração de uma corda de piano;
e) propagação sonora no ar.
6. Qual dos seguintes tipos de onda não é onda eletromagnética?
a) infravermelho
b) radiação gama
c) ondas luminosas
d) ondas sonoras
e) ondas de rádio
7. Na figura, o garoto faz com que a extremidade da corda em sua
mão realize um movimento periódico de sobe e desce.
Dessa forma, produz na corda o trem de ondas representado.
NOÇÕES GERAIS DE ONDAS
1. (FUND. CARLOS CHAGAS) – A propagação de ondas
envolve, necessariamente,
a) transporte de energia;
b) transformação de energia;
c) produção de energia;
d) movimento de matéria;
e) transporte de matéria e energia.
2. Nos modernos filmes de ficção científica, é muito comum observarmos naves espaciais que, durante combates em pleno cosmos (onde
reina o vácuo), disparam umas contra as outras, produzindo estrondos
emocionantes. Aponte a alternativa correta:
a) os estrondos referidos condizem com a realidade, pois o som
propaga-se no vácuo;
b) os estrondos referidos não condizem com a realidade, pois o som
não se propaga no vácuo;
c) os estrondos referidos, na realidade, são mais fortes que aqueles
exibidos no cinema;
84 –
As ondas presentes na corda são
a) mecânicas, longitudinais e planas;
b) mecânicas, mistas e circulares;
c) mecânicas, transversais e puntiformes;
d) eletromagnéticas, transversais e planas;
e) eletromagnéticas, mistas e esféricas.
8. (UNICAMP) – A figura 1 representa um pulso transversal propagando-se da esquerda para a direita numa corda ideal, longa e esticada. Num dado instante t0, os pontos A, B e C da corda encontram-se
nas posições indicadas na figura 2. Quais devem ser a direção e o
sentido da velocidade de cada um dos pontos A, B e C, no instante t0?
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 85
3. (FCC) – Uma onda sonora propaga-se no ar com velocidade V e
frequência f. Se a frequência da onda for duplicada,
a) o comprimento de onda duplica.
b) o comprimento de onda não se altera.
c) o comprimento de onda se reduz à metade.
d) a velocidade de propagação da onda dobra.
e) a velocidade de propagação da onda se reduz à metade.
9. Da janela de um apartamento situado no 10º andar de um edifício,
você observa um operário batendo um prego em uma tábua postada
sobre o solo. Você primeiramente vê a martelada para, depois de um
certo intervalo de tempo, ouvir o ruído correspondente. Dê uma explicação para o fato, justificando-a com dados numéricos.
10. Para pesquisar a profundidade do oceano numa certa região, usa-se
um sonar instalado num barco em repouso. O intervalo de tempo decorrido
entre a emissão do sinal (ultrassom de frequência 75 000 Hz) e a resposta
ao barco (eco) é de um segundo. Supondo a velocidade de propagação do
som na água 1500m/s, a profundidade do oceano na região considerada é
de:
a) 25m
b) 50m
c) 100m
d) 750m
e) 1500m
11. Um caçador ouve o eco de um tiro 6,0 segundos após ter disparado
a arma. Sabendo-se que o som se propaga no ar com velocidade de
340m/s, verifica-se que o anteparo refletor encontra-se a uma distância
igual a:
a) 2040m
b) 1020m c) 510m
d) 340m
e) 680m
4. (FATES) – Um surfista flutua com uma prancha em uma certa
praia. A cada 5 segundos, o surfista percebe que, devido às ondas, ele
sobe, e depois desce, 1,0m acima, e depois abaixo, do nível normal do
mar. Assim, pode-se concluir que a amplitude e a frequência das ondas
do mar naquele local valem, respectivamente:
a) 0,50m e 0,20Hz;
b) 1,0m e 0,20Hz;
c) 1,0m e 5,0Hz;
d) 2,0m e 0,20Hz;
e) 2,0m e 5,0Hz.
5. (UNIRIO) – O período de uma onda num lago é 2,0s e sua velocidade tem intensidade igual a 1,0m/s. Seu comprimento de onda é:
a) 0,50m
b) 1,0m
c) 1,5m
d) 2,0m
e) 3,0m
6. (UNIFOR) – Uma fonte emite ondas com frequência de 300Hz.
A velocidade de propagação dessas ondas, num certo meio, é de
600m/s. Nesse meio, o comprimento de onda, em cm, vale:
a) 25,0
b) 50,0
c) 100
d) 200
e) 500
7. A figura a seguir representa a foto de uma corda não absorvedora
de energia por onde se propaga um trem de ondas senoidais.
Sabendo-se que a frequência das ondas é igual a 10Hz, determine :
a) o período de oscilação da corda;
b) a amplitude e o comprimento de onda das ondas;
c) o módulo da velocidade de propagação das ondas.
MÓDULO 24
EQUAÇÃO FUNDAMENTAL DA ONDULATÓRIA V = λf
1. (EFOA) – Suponha uma onda de luz correspondente à cor violeta
e outra à cor vermelha, ambas propagando-se no vácuo, e considere as
grandezas físicas velocidade de propagação (V), comprimento de onda
() e frequência (f).
a) Indique, comparativamente, como cada uma dessas grandezas varia
de uma onda para outra.
b) Apresente uma fórmula geral que relacione essas três grandezas,
válida para qualquer onda.
2. (U.C. PELOTAS) – Assinale a alternativa correta.
a) O ultrassom possui comprimento de onda menor que o infrassom.
b) O ultrassom possui comprimento de onda maior que o infrassom.
c) A altura do som é a propriedade fisiológica que permite distinguir
um som forte de um som fraco.
d) Ao passar de um meio A para um outro meio, B, a velocidade do
som não se altera.
e) Nenhuma das afirmativas acima é correta.
8. A figura mostra o aspecto instantâneo de uma corda, por onde se
propaga um trem de pulsos senoidais, com velocidade de módulo
32cm/s.
– 85
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 86
Determine
a) o comprimento de onda correspondente ao caso;
b) a frequência dos pulsos.
9. A figura representa o perfil da superfície da água do mar num
determinado instante. Um observador em repouso aciona o seu
cronômetro quando uma primeira crista passa por ele e trava o
dispositivo um minuto depois, no instante em que a sétima crista passa por ele.
13. (SANTA CASA) – Uma estação de rádio emite ondas de frequência
3,33 megahertz. Se a velocidade de propagação dessa onda é de
300 000km/s, seu comprimento de onda, em metros, é um valor mais
próximo de:
a) 200
b) 150
c) 120
d) 90
e) 102
FRENTE 3
MÓDULO 19
CAMPO MAGNÉTICO DO
CONDUTOR RETILÍNEO E DA ESPIRA
A amplitude das ondas bem como sua velocidade de propagação valem,
respectivamente:
a) 4,0m e 0,60m/s
b) 2,0m e 0,60m/s
c) 2,0m e 1,2m/s
d) 4,0m e 1,2m/s
e) 1,0m e 0,60m/s
1. Na figura abaixo, temos um fio perpendicular a esta folha, percor
rido por uma corrente elétrica de sentido descendente, isto é, do leitor
para o papel. Três bússolas foram colocadas em torno do fio, todas no
plano deste papel, que é horizontal (polo N azul e polo S vermelho).
10. Na figura 1, tem-se uma corda esticada, de comprimento
–––
AB = 2,0m, em repouso, fixa em B. No instante t0 = 0, uma fonte F
começa a produzir em A ondas senoidais que se propagam ao longo da
corda. A figura 2 mostra o perfil da corda no instante t1 = 0,050s, quando
a frente da onda produzida por F atinge o ponto B.
a) Oriente a linha de indução que circula o fio e passa pelas bússolas.
b) Como ficam posicionadas as agulhas magnéticas de cada bússola?
Faça uma figura.
Calcule
a) a velocidade de propagação das ondas na corda;
b) a frequência de operação de F.
11. (MED. ABC) – O som pode ser percebido pelo ouvido humano
apenas na faixa entre 20Hz e 20 000Hz. Sendo a velocidade de
propagação do som na água de aproximadamente 1 500m/s, assinale a
afirmação correta para o maior e o menor comprimento de onda do
som, quando se propaga nesse meio.
a) 1,7 . 10m; 1,7 . 10–2m.
b) 2,5 . 102m; 2,5 . 10–1m.
–2
c) 7,5 . 10m; 7,5 . 10 m.
d) 2,5 . 102m; 1,7 . 10–2m.
–1
e) 7,5 . 10m; 2,5 . 10 m.
12. (UEL) – Uma onda periódica transversal propaga-se numa mola,
na qual cada ponto executa uma oscilação completa a cada 0,20s.
Sabendo-se que a distância entre duas cristas consecutivas é 30cm, pode-se concluir que a velocidade de propagação dessa onda é, em m/s,
igual a
a) 0,15
b) 0,60
c) 1,5 d) 3,0 e) 6,0
86 –
2. Na figura, vemos um plano horizontal PH, um fio condutor
retilíneo que o fura num ponto F e é perpendicular a ele. Vemos ainda
seis bússolas, três à direita do fio e três à sua esquerda, todas indicando
o polo norte geográfico.
Num dado instante, faz-se passar uma corrente elétrica muito intensa
no fio. O sentido dela é de baixo para cima. O que acontece com as
agulhas magnéticas?
a) Nenhuma delas se mexe.
b) As da direita giram 1/4 de volta no sentido horário e as da esquerda no sentido anti-horário.
c) As da direita giram 1/4 de volta no sentido anti-horário e as da
esquerda no sentido horário.
d) Todas giram 1/4 de volta no sentido horário.
e) Todas giram 1/4 de volta no sentido anti-horário.
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 87
3. (FUVEST) – A figura representa quatro bússolas apontando, inicialmente, para o polo norte terrestre. Pelo ponto O, perpendicularmente ao
plano do papel, coloca-se um fio condutor retilíneo e longo.
6. Qual a polaridade da espira abaixo:
a) vista pelo observador A?
b) vista pelo observador B?
Ao se fazer passar pelo condutor uma corrente elétrica contínua e intensa
no sentido do plano do papel para a vista do leitor, permanece(m) praticamente inalterada(s) (em equilíbrio estável) a(s) agulha(s)
a) das bússolas B e C.
b) das bússolas B e D.
c) das bússolas A, C e D.
d) somente da bússola C.
e) somente da bússola D.
4. (UFRS) – A figura mostra dois condutores longos, x e y, perpendiculares ao plano da página, percorridos por correntes elétricas
contínuas de iguais intensidades e sentidos para fora da página.
No ponto P, equidistante dos fios, o sentido do vetor indução magnética resultante produzido pelas duas correntes está corretamente
indicado pela seta
a) 1
b) 2
c) 3
d) 4
e) perpendicular à página e para desta.
5. (FUND. CARLOS CHAGAS) – Dois fios dispostos como indica a figura determinam as quatro regiões do plano.
7. Na figura que se segue, temos um solenoide e a representação de
linhas de indução do seu campo magnético interno.
Podemos afirmar que
a) X é polo sul e a corrente circula de M para N.
b) Y é polo norte e a corrente circula de N para M.
c) X é polo sul e a corrente circula de N para M.
d) Y é polo sul e a corrente circula de M para N.
e) X é polo norte e a corrente circula de M para N.
8. (FUND. CARLOS CHAGAS-PUC-BA) – Uma espira circular
é percorrida por uma corrente elétrica contínua, de intensidade constante. Quais são as características do vetor campo magnético no centro
da espira?
a) É constante e perpendicular ao plano da espira.
b) É constante e paralelo ao plano da espira.
c) No centro da espira é nulo.
d) É variável e perpendicular ao plano da espira.
e) É variável e paralelo ao plano da espira.
MÓDULO 20
INDUÇÃO ELETROMAGNÉTICA
As correntes elétricas I’, I’’, pelos condutores, podem produzir campos
de intensidade nula:
a) Somente em (I).
b) Somente em (II).
c) Somente em (III).
d) Em (II) e (IV).
e) Em (I) e (III).
1. (UFMG) – A corrente elétrica induzida em uma espira circular
será
a) nula, quando o fluxo magnético que atravessa a espira for constante.
b) inversamente proporcional à variação do fluxo magnético com o
tempo.
– 87
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 88
c) no mesmo sentido da variação do fluxo magnético.
d) tanto maior quanto maior for a resistência da espira.
e) sempre a mesma, qualquer que seja a resistência da espira.
2. (U.F. VIÇOSA-MG) – As figuras abaixo representam uma espira e um ímã próximos.
Das situações abaixo, a que não corresponde à indução de corrente na
espira é aquela em que
a) a espira e o ímã se afastam.
b) a espira está em repouso e o ímã se move para cima.
c) a espira se move para cima e o ímã para baixo.
d) a espira e o ímã se aproximam.
e) a espira e o ímã se movem com mesma velocidade para a direita.
Dadas as afirmativas:
I) O fluxo magnético no interior da espira ABCD está diminuindo,
em módulo.
II) A corrente induzida circula na espira no sentido anti-horário.
III) A força que atua na barra é perpendicular à velocidade.
Estão corretas:
a) Somente I.
b) Somente II.
c) Somente III.
d) Duas delas.
e) Todas.
5. (U.F.UBERLÂNDIA-MG) – Quando o fio móvel da figura é
deslocado para a direita, aparece no circuito uma corrente induzida i no
sentido mostrado.
3.
(UFPR) – A figura a seguir ilustra as posições relativas de um
ímã e um anel condutor, ambos inicialmente em repouso. Por 1 e 2
indicam-se possíveis sentidos de correntes elétricas induzidas no anel.
O campo magnético existente na região A
a) aponta para dentro do papel. b) aponta para fora do papel.
c) aponta para a esquerda.
d) aponta para a direita.
e) é nulo
MÓDULO 21
Julgue as proposições abaixo.
0. Não haverá correntes elétricas induzidas no anel, qualquer que seja
o movimento do ímã.
1. Ao aproximarmos o ímã do anel, haverá uma corrente elétrica
induzida no anel com sentido 1.
2. Ao afastarmos o ímã do anel, haverá uma corrente elétrica induzida
no anel com sentido 2.
3. Ao afastarmos o anel do ímã, haverá uma corrente elétrica induzida
no anel com sentido 1.
4. Ao aproximarmos o anel do ímã, haverá uma corrente elétrica
induzida no anel com sentido 1.
5. Não haverá corrente elétrica induzida no anel, qualquer que seja o
movimento dele.
4. (U.F.SC) – A figura abaixo representa um condutor colocado sob
a ação de um campo magnético constante, com uma barra metálica
→
apoiada sobre o condutor deslocando-se com velocidade v.
88 –
ELETROSTÁTICA: ELETRIZAÇÃO
POR ATRITO, CONTATO E INDUÇÃO
1. A unidade de carga elétrica no SI é o coulomb (C). Ele é definido
a partir de duas outras unidades básicas do SI: a de corrente elétrica, ou
seja, o ampère (A) e a de tempo, o segundo (s). Podemos afirmar que:
a) C = A . s
b) C = A/s
c) C = s/A
d) C = A . s2
e) C = A/s2
2. A uma esfera metálica, inicialmente neutra, foram acrescentados
2,0x1010 elétrons. Determine a carga elétrica da esfera. É dada a carga
elétrica elementar e = 1,6 x 10–19C.
3. (U.E.PI) – Temos quatro esferas metálicas idênticas: A, B, C e
D. Dessas quatro, apenas a esfera A está eletrizada. Se fizermos um
contato sucessivo da esfera A com cada uma das demais, qual é a carga
elétrica final da esfera A?
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 89
4. (FCC–BA) – Considere duas esferas metálicas idênticas. A carga
elétrica de uma é Q e da outra é –2Q. Colocando-se as duas esferas em
contato, a carga elétrica da esfera que estava, no início, carregada
positivamente fica igual a
a) 3Q/2
b) Q/2
c) –Q/2
d) –3Q/2
e) –Q/4
5. (MACKENZIE) – Em uma atividade no laboratório de Física,
um estudante, usando uma luva de material isolante, encosta uma
esfera metálica A, carregada eletricamente com 8 C, em outra idêntica
B, eletricamente neutra. Em seguida, encosta a esfera B em outra C,
também idêntica e eletricamente neutra. A carga adquirida pela esfera
C é:
a) 2 C
b) 4 C
c) 6 C
d) 8 C
e) 9 C
Nessa configuração, a intensidade da força elétrica que age sobre uma
carga de prova negativa, colocada no centro do anel (ponto P), é F1. Se
forem acrescentadas sobre o anel três outras cargas de mesmo módulo
Q, mas positivas, como na figura II, a intensidade da força elétrica no ponto P passará a ser
a) zero
b) (1/2)F1
c) (3/4)F1 d) F1
e) 2 F1
Observação: 1,0C = 10–6C (leia: microcoulomb)
6. (ITA) – Têm-se três pequenas esferas carregadas com cargas q1,
q2 e q3. Sabendo-se que
MÓDULO 22
FORÇA ELETROSTÁTICA
1. (FUVEST) – Duas partículas, eletricamente carregadas com
+ 8,0 . 10–6C cada uma, são colocadas no vácuo a uma distância
N . m2
de 30cm, onde K0 = 9 . 109 ––––––
C2 . A força de interação eletrostática
entre essas cargas é:
a) de repulsão e igual a 6,4N.
b) de repulsão e igual a 1,6N.
c) de atração e igual a 6,4N.
d) de atração e igual a 1,6N.
e) impossível de ser determinada.
2. No vácuo, foram colocadas duas cargas elétricas idênticas com
+4,0C cada uma, a uma distância de 4,0 x 10–3m. Sabendo que, no
vácuo, a constante eletrostática vale 9,0 x 109 unidades SI, determine
a intensidade da força eletrostática.
3. Duas partículas eletrizadas com cargas elétricas opostas, + 2,0C
e –2,0C, são colocadas, no vácuo, próximas uma da outra e atraemse com uma força de intensidade F = 9,0 x 103N. Determine a distância
que as separa. Use K0 = 9,0 x 109 unidades SI.
4. (AFA) – Duas esferas iguais, carregadas com cargas +16C e
–4,0C são colocadas em contato uma com a outra e, depois, separadas
pela distância de 3,0cm. A intensidade da força de repulsão, em
newtons, entre elas será: (K0 = 9 . 109uSI)
a) 19
b) 50
c) 160
d) 360
e) 540
5. (FUVEST) – Pequenas esferas, carregadas com cargas elétricas
negativas de mesmo módulo Q, estão dispostas sobre um anel isolante e circular, como indicado na figura I.
1.
estas três esferas estão colocadas no vácuo, sobre um plano horizontal sem atrito.
2. os centros dessas esferas estão em uma mesma horizontal.
3. as esferas estão em equilíbrio nas posições indicadas na figura
anterior.
4. a carga da esfera q2 é positiva e vale 2,7 . 10–4C.
5. d1 = d2 = 0,12m
a) Quais os sinais das cargas q1 e q3?
b) Quais os módulos de q1 e q3?
MÓDULO 23
CAMPO ELÉTRICO
1. (MACKENZIE) – Uma carga elétrica puntiforme com 4,0C,
que é colocada em um ponto P do vácuo, fica sujeita a uma força elétrica de intensidade 1,2N. O campo elétrico nesse ponto P tem intensidade de:
a) 3,0 . 105 N/C
b) 2,4 . 105 N/C c) 1,2 .105 N/C
d) 4,0 . 10–6 N/C
e) 4,8 . 10–6 N/C
2. (FCC) – Uma carga pontual Q, positiva, gera no espaço um
campo elétrico. Num ponto P, a 0,5m dela, o campo tem intensidade
E = 7,2 . 106N/C. Sendo o meio o vácuo, onde K0 = 9 . 109 unidades
S.I., determine Q.
a) 2,0 . 10–4 C
b) 4,0 . 10–4 C
c) 2,0 . 10–6 C
d) 4,0 . 10–6 C
e) 2,0 . 10–2 C
– 89
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 90
3.
Considere as três figuras a seguir.
Calcule a massa de um ponto material eletrizado com carga de +8C
que, ao ser colocado em B, permaneceu em equilíbrio.
2. Uma partícula de massa M e carga Q negativa está em equilíbrio,
parada, sob a ação de um campo elétrico vertical e do campo de
gravidade. Sendo g o módulo da aceleração da gravidade, determine
a) o sentido do vetor campo elétrico;
b) a intensidade do vetor campo elétrico no ponto onde a partícula está
em equilíbrio.
Nelas, temos:
Q = carga elétrica puntiforme geradora do campo elétrico
3. Determine o módulo do campo resultante em P, gerado pelas
cargas (+Q) e (–Q) da figura. O meio é o vácuo.
Dados: K0 = 9 . 109 unidades S.I.
Q = 4 . 10–8C
q = carga elétrica de prova
→
F = força elétrica sobre a carga de prova
→
E = vetor campo elétrico gerado pela "carga fonte" Q
Analise cada figura e descubra o sinal das cargas elétricas q e Q.
Pode-se dizer que:
I)
Na figura (1):
II) Na figura (2):
III) Na figura (3):
IV) Em todas as figuras:
Q>0eq>0
Q<0eq>0
Q<0eq<0
q>0
Use, para a resposta, o código abaixo:
a) Se todas forem verdadeiras.
b) Se, apenas, I, II e IV forem verdadeiras.
c) Se, apenas, I e III forem verdadeiras.
d) Se, apenas, II for verdadeira.
e) Se nenhuma for verdadeira.
MÓDULO 24
CAMPO ELÉTRICO RESULTANTE
1. Na região abaixo limitada, temos um campo elétrico de intensidade E = 40N/C. Admita ainda g = 10m/s2.
90 –
4. Determine a direção e o sentido do campo elétrico resultante no
terceiro vértice do triângulo equilátero ABC.
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 91
FRENTE 1
FRENTE 2
MÓDULO 19
1)
2)
5)
6)
MÓDULO 19
a) Fat = 9,0N e a = 0
b) Fat = 8,0N e a = 2,0m/s2
0,50
3) 20N
4) E
a) 2,25m/s2
b) 2,25N
a) 1,0m/s2
b) 90N
c) 30N
1) C
4) a) 30°
2) B
b) Reflexão total
3) D
MÓDULO 20
1)
2)
3)
4)
a) 6,0m/s2
a) diminui
a) 2,0m/s2
B
b) 0,75
b) 2,0m/s2
b) 4,0m
5) A
MÓDULO 20
MÓDULO 21
1)
4)
1,0kN
a) 2,0kN
5)
m/s
15
2) 8,0km/s
b) 14,0kN
3) D
E
a) 24N
a) 60kg
4)
5)
gR
2) B
9) A
3) C
10) A
4) C
11) D
5) B
6) C
7) A
MÓDULO 21
MÓDULO 22
1)
2)
3)
1) B
8) D
1) A
2) A imagem é virtual e forma-se sobre o foco F.
3) a) 22cm
b) 8 vezes (imagem invertida)
b) 54N
b) 2,0m/s
4)
40cm
5) 10cm
4
6) 4cm ou ––– cm
3
7) 25cm
80m
MÓDULO 22
MÓDULO 23
1)
p = F = 0 ; F = 25,0J ; F = –10,0J
2)
3)
5)
E; Nota: o trabalho do atrito vale –120J.
D
4) A
a) V = 3,0 + 2,0t (SI)
b) 8,0 . 102 J
N
1
MÓDULO 24
1) a) 0,50
b) – 3,0 . 104J
2) D
3) E
4) a) 15J
b) 5m/s
5) a) 17m/s2
b) 10m/s
6) a) 1,25 . 102J e – 1,0 . 102J
b) 5,0m/s
2
1)
3)
4)
C
2) Corretas: (1), (2) e (3)
As lentes são divergentes com distância focal de – 50cm.
E
5) B
MÓDULO 23
1) A
8)
2) B
3) A
4) B
5) E
6) D
7) C
9)
O fato ocorre devido à informação luminosa viajar com velocidade muito maior que a informação sonora.
Vluz 3,0 . 108 m/s
Vsom 340 m/s
10)D
11)B
– 91
C3_3a_Soroc_Fis_Exerc_alelex_2014 05/03/14 15:51 Página 92
MÓDULO 24
MÓDULO 21
1) a) Vvi = Vve; fvi > fve e vi < ve
b) V = f
2) A
3) C
7) a) 0,10s
b) 0,50m e 1,0m
c) 10m/s
10)a) 40m/s
11) C
b) 80Hz
1) A
4) B
8) a) 4,0cm
b) 8,0Hz
5) D
9) B
12) C
6) D
13) D
MÓDULO 19
2) C
3) D
4) D
4) C
5) A
MÓDULO 22
FRENTE 3
1)
2) –3,2 x 10–9 C
3) 1/8 da carga inicial
1) A
2)
9,0 x 103N
3) 2,0 x 10–3 m
4) D
5)
E
6) a) negativos
b) |q1| = |q2| 1,1 x10–3C
5) D
MÓDULO 23
1) A
6) a) sul
b) norte
7)A
8) A
MÓDULO 20
2) A
MÓDULO 24
1) m = 3,2 . 10–5kg
2) a)
para baixo, pois Q < 0
b)
M.g
E = ––––––
|Q|
3) Eresp = 180N/C
1)
3)
4)
A
2) E
1, 2 e 4 verdadeiras; 0, 3 e 5 falsas.
D
5) A
92 –
3) C
4)
→
Eres