capítulo 2 – radiação solar e terrestre

1
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
CAPÍTULO 2 – RADIAÇÃO SOLAR E TERRESTRE
2.1. O ESPECTRO ELETROMAGNÉTICO
O espectro de emissão do sol apresenta intensas variações decorrentes da absorção dos componentes
atômicos, como hidrogênio, magnésio, alumínio, etc., presentes na atmosfera solar. Esses espectros de
absorção são denominados Linhas de Fraunhofer, em homenagem ao seu descobridor Joseph Fraunhofer
(1887-1826), e permitem analisar a composição
química do Sol à distância. A emissão ou
absorção de um fóton por um átomo se realiza
quando um elétron muda de órbita. A emissão
ocorre se o nível de energia da órbita de chegada é
menor que o do nível de partida, com o contrário
ocorrendo na absorção. Quando o equilíbrio
termodinâmico é atingido, ou seja quando o fluxo
de energia emitido é igual ao absorvido, o
elemento passa a atuar como um corpo negro. No
caso da fotosfera, a temperatura decresce com a
altitude e, portanto, um fóton que escapa atravessa
um meio mais frio. Desse modo, ele será
absorvido por átomos em temperatura inferior e,
por
conseqüência,
com
taxas
de
emissão
inferiores. Há, portanto, um déficit que pode ser
traduzido por uma absorção. Pode-se dizer que o
Sol emite energia em, praticamente, todos os
comprimentos
de
onda
do
espectro
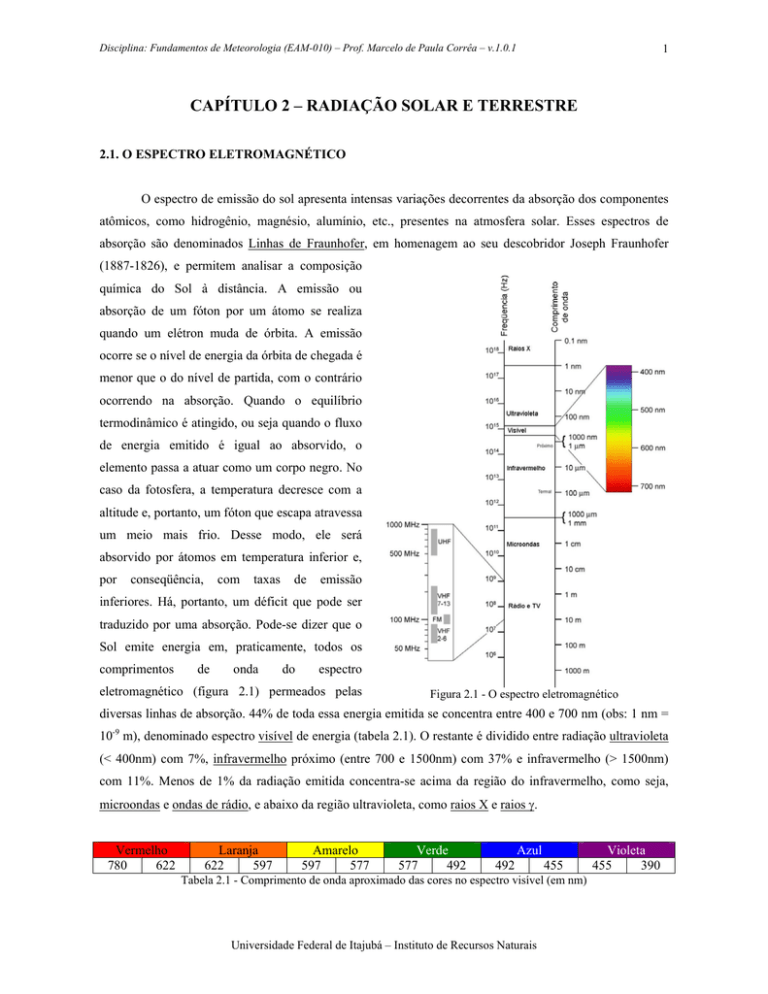
eletromagnético (figura 2.1) permeados pelas
Figura 2.1 - O espectro eletromagnético
diversas linhas de absorção. 44% de toda essa energia emitida se concentra entre 400 e 700 nm (obs: 1 nm =
10-9 m), denominado espectro visível de energia (tabela 2.1). O restante é dividido entre radiação ultravioleta
(< 400nm) com 7%, infravermelho próximo (entre 700 e 1500nm) com 37% e infravermelho (> 1500nm)
com 11%. Menos de 1% da radiação emitida concentra-se acima da região do infravermelho, como seja,
microondas e ondas de rádio, e abaixo da região ultravioleta, como raios X e raios γ.
Vermelho
780
622
Laranja
622
597
Amarelo
597
577
Verde
577
492
Azul
492
455
Tabela 2.1 - Comprimento de onda aproximado das cores no espectro visível (em nm)
Universidade Federal de Itajubá – Instituto de Recursos Naturais
Violeta
455
390
2
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
É importante lembrarmos que a radiação emitida pelo sol, assim como toda radiação
eletromagnética, viaja a velocidade da luz, isto é, aproximadamente, 300.000 km/s. Deste modo, pode–se
estabelecer uma relação entre a velocidade da luz (v [m/s]), o comprimento de onda (λ [m]) e a freqüência da
onda (f [Hz]):
v = λf
(2.1)
2.2. GRANDEZAS RADIOMÉTRICAS
Nesta seção vamos conhecer algumas das grandezas mais usuais do estudo da radiação.
a) Fluxo (F): É a potência radiante. Ou seja, é quantidade de energia (U) observada (ou detectada) por
unidade de tempo. (Unidade: W, que corresponde a J/s)
F=
ΔU
Δt
(2.2)
b) Intensidade (P): É o quociente entre o fluxo observado associado a um dado feixe, num dado ponto do
espaço, e o ângulo sólido correspondentes à origem ou ao destino deste fluxo. (Unidade: W/sr)
P=
ΔU
ΔtΔΩ
(2.3)
Mas o que é o ângulo sólido ?
Um ângulo plano (α) corresponde a um arco de comprimento L sobre um círculo de raio R, tal que α = L/R
radianos. Por analogia, um ângulo sólido (Ω) corresponde a uma superfície de área A sobre uma esfera de
raio R, tal que Ω = A/R2 ster–radianos. A figura 2.2 mostra uma representação do ângulo sólido.
figura 2.2 - Ângulo sólido
c) Irradiância (I): É o quociente entre o fluxo observado num certo elemento de superfície de área deste
elemento. (Unidade: W/m2).
Universidade Federal de Itajubá – Instituto de Recursos Naturais
3
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
I=
ΔU
Δt Δ A
(2.4)
No caso de irradiância emitida por uma fonte, denominamos de emitância (E).
d) Radiância (L): É uma medida da quantidade de radiação, recebida por um ponto ou emitida por
uma fonte, em uma determinada direção. Isto é, é o quociente entre a intensidade observada num certo
elemento de superfície, numa dada direção, e a área da projeção ortogonal deste elemento de superfície num
plano perpendicular à direção tratada. (Unidade: W/m2sr)
L=
P
ΔA cos θ
(2.5)
Substituindo 2.3 em 2.5, tem–se que:
ΔU = LΔtΔAΔΩ cos θ
(2.6)
Por exemplo, se numa determinada situação a radiância é constante, então a quantidade de energia vai
diminuir (ΔU < 0), quando: 1) a duração do fluxo for menor (Δt < 0); ou 2) quando a área diminuir (ΔA < 0);
ou 3) quando o ângulo sólido for mais estreito (ΔΩ < 0); ou ainda, 4) quando o ângulo de inclinação do feixe
se aproximar do horizonte (θ for pequeno).
Figura 2.3 – radiância
e) Dose (D): Integrando-se a irradiância durante um certo intervalo de tempo obtém-se a dose total de
energia recebida por um certo alvo. (Unidade: J/m2)
D = ∫ Idt IΔt
Δt
Universidade Federal de Itajubá – Instituto de Recursos Naturais
(2.7)
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
4
ER 2.1. Uma estrela de raio R tem certa temperatura T. Essa estrela emite energia a uma taxa igual a Eo
W/m2, de forma isotrópica para todo espaço. Calcule o fluxo e a intensidade de energia emitida por essa
estrela.
Resolução
Supondo que a estrela seja uma esfera, um observador receberá a energia emitida por um círculo de área A =
4πR2.
Das equações 2.2 e 2.4, temos que o fluxo será dado por: I =
F
F
⇒ Io =
⇒ F = E o 4πR 2
4πR 2
ΔA
Das equações 2.2 e 2.3, tiramos que a intensidade é dada por: P =
F
ΔΩ
Como o ângulo sólido é um círculo completo, temos que ΔΩ = 4π, então: P = EoR2.
2.3. INTERAÇÃO DA RADIAÇÃO COM OS MATERIAIS
A radiação solar interage com os elementos que compõem a atmosfera terrestre, tais como
moléculas, gases, nuvens, aerossóis, etc., e, também, com aqueles que estão sobre a superfície terrestre. Isto
é, quando a radiação solar atinge o topo da atmosfera e viaja até a superfície, sofre atenuações devidas às
interações com estes elementos. Deste modo, definimos a atenuação como a subtração de uma fração de
energia do fluxo incidente.
A atenuação se dá por meio da absorção ou do espalhamento da radiação em outras direções que não
a do alvo em superfície. A absorção é a fração subtraída do fluxo incidente que é incorporada à energia
interna do meio atravessado. Portanto, parte da energia é retirada do feixe, causando um aumento da energia
interna do elemento de volume (Por esse motivo, é relacionada ao aquecimento de camadas atmosféricas). O
espalhamento é a fração subtraída do fluxo incidente que é re-irradiada para diferentes direções do espaço.
Parte da radiação não sofre nenhum tipo de interação e é inteiramente transmitida, através do volume de
matéria, no mesmo sentido do feixe incidente.
Na figura 2.4 temos um esquema dessas interações com base na energia solar atravessando a
atmosfera terrestre.
Figura 2.4 – atenuação da radiação incidente por um elemento de matéria
Universidade Federal de Itajubá – Instituto de Recursos Naturais
5
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
No entanto, os corpos que absorvem radiação, emitem parte da mesma em diferentes comprimentos
de onda. Deste modo, a radiação recebida pelo alvo sofre um acréscimo de energia devido a emissão do
elemento de matéria.
Figura 2.5 – interação entre a radiação incidente e um elemento de matéria
Finalmente, o elemento de matéria também pode receber energia de outras fontes e espalhar esta
energia na direção do alvo. Desta forma, a radiação que atinge o alvo receberá um incremento de energia e
temos a seguinte configuração:
Figura 2.6 – interação entre a radiação incidente e um elemento de matéria (2)
Assim, num caso típico da radiação solar atravessando a atmosfera, a radiação medida em um
determinado alvo à superfície é dada pela relação:
R alvo = RI − RE − RA + RM + RO
(2.8)
2.3.1. O espalhamento de radiação solar na atmosfera terrestre
Parte da radiação solar que atravessa a atmosfera é espalhada, ou seja, tem sua direção e sentido
desviados por moléculas e partículas presentes no caminho óptico. A natureza do espalhamento depende do
tipo de agente que realiza tal fenômeno. Isto é, o espalhamento causado por uma molécula de um gás tem
características distintas do espalhamento causado por um aerossol ou por uma gotícula de nuvem. Além do
agente causador, o espalhamento também vai depender do comprimento de onda da radiação. Por exemplo, a
Universidade Federal de Itajubá – Instituto de Recursos Naturais
6
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
radiação ultravioleta é espalhada com mais intensidade por uma molécula do que a radiação visível. Deste
modo, a medida do espalhamento vai depender destes dois fatores: o comprimento de onda e a natureza do
agente espalhador.
Espalhamento Rayleigh é nome dado ao espalhamento de radiação por partículas muito pequenas, de
forma que o comprimento de onda da radiação incidente seja muitas vezes maior do que a dimensão da
partícula (r << λ). Esse tipo de fenômeno para radiação solar é geralmente promovido por moléculas e micropartículas em suspensão na atmosfera e, por esta razão, é também chamado de espalhamento molecular. Esse
tipo de interação começou a ser estudado no século XIX, por Lord Rayleigh (1842-1919), em virtude de
observações da luz e da coloração do céu. No espalhamento Rayleigh a intensidade do espalhamento
molecular é inversamente proporcional à quarta potência do comprimento de onda. Esta relação é a
responsável pela coloração azul do céu. Apesar de a cor violeta apresentar o menor comprimento de onda e,
portanto, a melhor eficiência de espalhamento, é a cor azul que se faz notar com maior facilidade. Isso
acontece pois a radiação de cor azul é transmitida com maior facilidade através da atmosfera e, também, por
que o olho humano é mais sensível à comprimentos de onda próximos do azul.
No caso de partículas maiores, como aerossóis e gotas em nuvens, o espalhamento recebe o nome de
espalhamento Mie, devido ao tratamento físico e matemático adotado para o fenômeno. Ao contrário dos
gases, o espalhamento da radiação por partículas possui um grau de complexidade maior. Por exemplo, a
variabilidade das características físico-químicas dos aerossóis é tamanha que não se pode generalizar o
conhecimento adquirido sobre a forma do espalhamento e suas dependências com o comprimento de onda.
Um exemplo dessa heterogeneidade é apresentado na tabela 2.2 com uma divisão simplificada das quatro
categorias básicas de partículas em suspensão na atmosfera:
Nome
Aerossóis
Gotas (nevoeiro)
Gotas (chuva)
Cristais de gelo
Raio
0,1 – 1 μm
0,1 – 1 μm
1 – 10 μm
1 – 100 μm
Forma
irregular
esférica
esférica
irregular
Índice de refração
altamente variável
Conhecido
Conhecido
Conhecido
Tabela 2.2 - Características das partículas em suspensão na atmosfera
O tratamento matemático do espalhamento Mie se baseia na hipótese de que as partículas são esferas
homogêneas e com intensa descontinuidade do índice de refração em suas superfícies. Neste caso, considerase também que a radiação é espalhada igualmente em todos os comprimentos de onda. Por esta razão, as
nuvens parecem brancas. Em dias muito poluídos e, portanto, com alta concentração de aerossóis a névoa
também é esbranquiçada.
O pôr e o nascer do sol têm cores que tendem para o amarelo e o vermelho. Nestes casos a luz tem
que atravessar um caminho óptico bem maior e, portanto, a atenuação de radiação também é maior. Como os
comprimentos de onda menores espalham com mais facilidade, resta apenas radiação de comprimentos de
onda maiores, portanto, amarelo ou vermelho.
Quando o raio das partículas é muito maior que o comprimento de onda da radiação, a distribuição
angular da radiação espalhada é descrita pelos princípios da óptica geométrica. Neste caso está o
Universidade Federal de Itajubá – Instituto de Recursos Naturais
7
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
espalhamento de luz visível por gotas de chuva ou gotas maiores em nuvens e partículas de gelo. Este tipo de
fenômeno explica a formação de arco íris, auréolas, halos, coroas, dentre outros.
Sugestão: Realizar uma pesquisa sobre fenômenos ópticos como arco íris, auréolas, halos, coroas, etc.
2.3.2. Absorção de radiação solar na atmosfera terrestre
Quando um feixe de radiação atravessa um determinado volume de gás, parte de sua energia pode
ser absorvida pelas moléculas e átomos presentes nesse volume. Em contrapartida essa mesma massa de gás
pode emitir energia em outros comprimentos de onda. Esses fenômenos se refletem tanto no balanço da
energia mecânica, relacionada aos modelos de translação, rotação e vibração da molécula, quanto no balanço
da energia eletrônica, relacionado à estrutura detalhada do núcleo e dos elétrons. Neste nível, a absorção e a
emissão são observadas quando os elétrons sofrem transições de um estado para outro de energia. As
primeiras investigações sobre as transições eletrônicas tiveram início no começo do século XX, em estudos
sobre o espectro do átomo de hidrogênio, onde se mostrou que as órbitas circulares dos elétrons são
quantizadas. Isto é, que seus momentos angulares são múltiplos de um valor básico. Dessa forma, os átomos
podem existir em certo estado básico, de nível mínimo de energia, no qual não há emissão de radiação. A
mesma só ocorre quando o átomo realiza uma transição de certo estado de energia Ei para outro inferior, Ei-1.
A absorção, por sua vez, ocorre de maneira inversa, quando o elétron salta para uma órbita posterior. Neste
caso, se diz que o átomo está em seu estado excitado. Matematicamente tem-se que:
Ii − Ii −1 = hf
(2.9)
Onde hf representa o quantum de energia contido no fóton emitido durante a transição (h = constante de
Planck = 6,626068 × 10-34 m2 kg/s). Essa equação é denominada relação de Planck.
No espectro solar, os principais gases absorvedores são o vapor d’água, o oxigênio, o ozônio, o
nitrogênio, o gás carbônico, além das espécies monoatômicas do oxigênio e nitrogênio. Outros espectros de
absorção são observados para constituintes menores como o monóxido de carbono, a amônia e o óxido
nitroso. Os espectros de absorção devido às transições eletrônicas do oxigênio e nitrogênio, atômicos e
moleculares, ocorrem predominantemente na região ultravioleta, enquanto aquelas relacionadas às transições
vibracionais de moléculas triatômicas como o vapor d’água, ozônio e gás carbônico ocorrem na região do
infravermelho.
Na figura 2.7 são apresentados os espectros de absorção. Observa-se que abaixo de 0,3 μm a
radiação é completamente absorvida pelo ozônio e oxigênio estratosféricos. Portanto, dizemos que a
atmosfera é opaca para a radiação neste intervalo espectral. Entre 0,3 e 0,8 μm, na região visível e no final do
espectro UV, a atmosfera é praticamente transparente. Ou seja, quase toda radiação solar atinge a superfície.
A região infravermelha é de forte absorção, principalmente pelo vapor d’água e pelo gás carbônico. Somente
entre 8 e 12 μm é que também há uma grande região transparente, com exceção da banda de 9,6 μm onde o
ozônio absorve fortemente. Esta região de transparência é chamada de janela atmosférica.
Universidade Federal de Itajubá – Instituto de Recursos Naturais
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
8
Figura 2.7 – Espectros de absorção (adaptado de Varejão-Silva, 2005)
Observa-se, portanto, características bem marcantes para a radiação. Enquanto a atmosfera é
praticamente transparente para a radiação solar, ela é praticamente opaca para a radiação terrestre (com
exceção da janela atmosférica). Esse comportamento explica o efeito estufa, que podemos entender fazendo
uma analogia com um carro parado sob o sol. A radiação solar penetra o vidro, mas a radiação de onda longa
(emissão) não consegue sair. Resultado: aumento excessivo de temperatura dentro do carro. Parte do balanço
de radiação do planeta é controlado pelas nuvens que refletem a radiação solar e absorvem fortemente a
radiação terrestre, inclusive na região da janela atmosférica. Com isto, evita-se um forte aquecimento diurno
e um forte resfriamento noturno.
2.4. CONCEITOS BÁSICOS IMPORTANTES
Nesta seção serão definidos alguns conceitos importantes para o estudo da radiação atmosférica.
a) Corpo negro (CN): Trata-se de um corpo hipotético capaz de absorver toda radiação incidente sobre ele.
b) Emissividade (ελ): É definida como a razão entre a energia emitida por um determinado corpo, num
determinado comprimento de onda, e a correspondente energia emitida por um CN à mesma temperatura do
corpo considerado. Portanto, εCN = 1.
c) Absortância (aλ): É a razão entre a quantidade de energia absorvida e o total de energia que incide sobre
um volume de matéria, para um dado comprimento de onda. Portanto, aCN = 1.
Universidade Federal de Itajubá – Instituto de Recursos Naturais
9
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
d) Refletância (rλ): É a relação entre a energia refletida para o hemisfério de origem e a radiação incidente,
para um dado comprimento de onda. Pela definição de CN, rCN = 0.
e) Transmitância (tλ): É a relação entre a energia transmitida e o total incidente, para um dado comprimento
de onda. Um CN tem tCN = 0.
Pela Lei da Conservação de Energia, temos:
a λ + rλ + t λ = 1
(2.10)
2.5. LEIS DA RADIAÇÃO
2.5.1. Lei de Planck (Max Planck, 1900)
Estabelece a distribuição espectral associada à máxima radiância espectral que pode ser emitida por
um corpo em equilíbrio termodinâmico à uma dada temperatura T. A energia emitida por um corpo negro é
depende de sua temperatura e do comprimento de onda em questão. Matematicamente é dada por:
LλCN =
2hc 2
λ 5 ⎡⎣exp ( hc λKT ) − 1⎤⎦
[W m-2 sr-1 /m]
(2.11)
Onde: c = velocidade da luz no vácuo = 299.792.458 m/s ≈ 3 × 108 m/s;
h = constante de Planck = 6,6262 × 10-34 Js;
K = constante de Boltzmann = 1,3807 × 10-23J/K;
T = temperatura do corpo negro [K];
λ = comprimento de onda [m].
A equação 2.11 também pode ser expressa em termos de freqüência (Hz) da onda eletromagnética:
LfCN =
2hf 3
c 2 ⎡⎣ exp ( hf KT ) − 1⎤⎦
[W m-2 sr-1 /Ηz]
(2.12)
2.5.2. Lei do deslocamento de Wien (Wilhelm Wien, 1894)
Estabelece uma relação de proporcionalidade inversa entre a temperatura de um corpo negro e o
comprimento de onda associado ao máximo relativo da respectiva função de Planck. Ou seja, a derivada, em
Universidade Federal de Itajubá – Instituto de Recursos Naturais
10
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
função do comprimento de onda, da função de Planck é nula para o comprimento de onda cuja emitância é
máxima.
∂
E λ = 0 ⇒ λ = λ máx
∂λ
Portanto, para o comprimento cuja emitância espectral seja máxima, temos:
λ máx T = cte = 2,897756 × 10−3 mK
(2.13)
Esta constante é denominada Constante de Wien.
ER 2.2. Considerando que a Terra e o sol emitam como corpos negros a temperaturas aproximada de 300 e
5770 K, aproximadamente, determine o comprimento de onda de máxima emissão destes astros.
Resolução
Da equação 2.13, tem-se:
Para a Terra: λ T .300 = 2,897756 × 10−3 ⇒ λ T = 9, 7 × 10−6 = 9, 7μm
Para o Sol: λS .5770 = 2,897756 × 10−3 ⇒ λS = 5, 0 × 10−7 = 0,5μm
A Terra tem o pico de emissão em torno de 10μm (infra-vermelho), enquanto o sol tem o pico de emissão em
0,5μm (região visível do espectro). Pela lei de Planck, é fácil verificar que a Terra emite radiação entre 3,0 e
200 μm e o sol emite entre 0,2 e 3,0 μm. Por este motivo, chamamos a radiação solar de radiação de onda
curta e a radiação terrestre de radiação de onda longa.
2.5.3. Lei de Stefan-Boltzmann (Josef Stefan, 1879; Ludwig Boltzmann, 1884)
Estabelece uma relação de proporção direta entre a irradiância emitida por um corpo negro, já
integrada sobre todo espectro eletromagnético, e a quarta potência da temperatura deste corpo. Se
integrarmos a equação 2.11 em todo espectro eletromagnético, vamos obter a radiância integrada, ou seja:
∞
L(T) = ∫ LλCN dλ
0
∞
L(T) = ∫ L λCN dλ =
0
∞
2K 4 T 4
x3
2π 4 K 4 4
d
λ
=
T
c2 h 3 ∫0 e x − 1
15c 2 h 3
Onde x = hc/λKT. Para determinarmos a emitância devemos integrar L(T) no hemisfério:
Universidade Federal de Itajubá – Instituto de Recursos Naturais
(2.14)
11
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
E=
π
2π 2
∫ ∫ cos θL(T)senθdθdφ = πL(T)
(2.15)
0 0
Substituindo 2.14 em 2.15, tem-se:
E=
2 π5 K 4 4
T = 5, 67 × 10−8 T 4
15c2 h 3
A constante é denominada constante de Stefan-Boltzmann (σ) e esta equação é rescrita como:
E = σT 4
(2.16)
ER 2.3. Determine a emitância radiante total de um corpo negro à temperatura do sol (~5770K) e à
temperatura da Terra (~300 K)
Resolução
E = σT 4 →
ES = 5,67.10-8.(5770)4 = 6,28.107 Wm-2 = 62,8 MWm-2
ET = 5,67.10-8.(300)4 = 459,3 Wm-2
ER 2.4. Determine a emitância espectral de um corpo negro à temperatura do Sol (5770 K), na faixa verde
do espectro eletromagnético.
Resolução
De acordo com a tabela 2.1, o verde está no intervalo espectral entre 492 e 577 nm.
Para avaliarmos a emissão neste intervalo espectral, vamos considerar a equação 2.14 da seguinte forma:
577
L(T) =
∫
LλCN dλ =
492
2K 4 T 4
c2 h 3
577
x3
∫ ex − 1 dx , para x = hc/λKT.
492
A fração x não depende só de λ ou de T, mas sim do produto entre ambos. Isto quer dizer que, por exemplo,
a fração da intensidade emitida por um corpo negro na região do espectro entre 0 e 10 nm a 1000 K é a
mesma que a fração da intensidade emitida entre 0 e 5 nm a 2000 K. Para calcular a integral devemos usar o
método de Simpson ou a seguinte aproximação:
Vamos definir a função F(x) dada por:
∞
∞
15 x 3
15 x 3e − x
F(x) = 4 ∫ x
dx = 4 ∫
dx
π x e −1
π x 1 − e− x
Universidade Federal de Itajubá – Instituto de Recursos Naturais
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
12
O termo 1–e–x pode ser expresso como uma soma de potências e–x desenvolvendo-se o binômio
(1-z)-1 =1+z+z 2 +z3 +z 4 +... . Então:
∞
F(x) =
15 3 − x
x e (1+z+z 2 +z3 +z 4 +...)dx
π4 ∫x
F(x) =
15 ∞ exp(− nx) ⎛ 3 3x 2 6x 6 ⎞
∑ n ⎜ x + n + n 2 + n3 ⎟
π4 n =1
⎝
⎠
Integrando por partes, temos:
Usando uma planilha excel ou um fazendo um pequeno programa em Fortran, podemos calcular F(x492) e
F(x577). A intensidade total emitida neste espectro será de:
E = [F(x1 ) − F(x 2 )]σT 4
Desta equação podemos tirar as seguintes conclusões: A baixas temperaturas praticamente toda radiação é
infravermelha. A altas temperaturas a contribuição da radiação UV é cada vez maior e as radiações visível e
IV se fazem cada vez menores. A contribuição de radiação visível é máxima em 7100 K.
Podemos também tirar conclusões acerca da cor aparente de um corpo a uma data temperatura. Por exemplo,
a 2000 K um corpo emite luz em todo espectro visível, mas a maior intensidade se dá no vermelho extremo
(baixa freqüência e comprimento de onda grande) e o corpo é visto como um vermelho brilhante. A 3000 K,
a temperatura aproximada de uma lâmpada incandescente, a quantidade relativa de luz azul aumenta, mas
ainda predomina a componente vermelha. Portanto, a vemos num tom amarelado. A 6000 K, que é
aproximadamente a temperatura do sol, a distribuição é quase uniforme em todo o visível e o corpo aparece
branco brilhante. Acima de 10000 K a luz azul é emitida com maior intensidade que a vermelha e o corpo é
visto em tom azulado (estrelas quentes).
O resultado obtido para a emissão de um corpo negro à temperatura de 5770 K, no espectro de cor
verde, é de, aproximadamente, 6,9×106 W/m2.
Sugestão: Reproduza este resultado, faça o mesmo para outros espectros e compare.
2.5.4. Lei de Kirchhoff (Gustav Kirchhoff, 1859)
A emissividade de um corpo, para um dado comprimento de onda, dividida pela absortância deste
mesmo corpo, para o mesmo comprimento de onda, é igual a emissividade de um corpo negro. Ou seja, a
energia absorvida por um corpo a uma dada temperatura em um determinado comprimento de onda é igual a
energia emitida por esse corpo a esta mesma temperatura e a este mesmo comprimento de onda. Ou seja, aλ =
ελ.
Universidade Federal de Itajubá – Instituto de Recursos Naturais
13
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
ελ
= 1 = εCNλ
aλ
(2.17)
Para um corpo não-negro (denominado corpo cinza), a emissividade é menor do que 1. Neste caso a
emitância é dada pela seguinte equação:
εCCλ =∈λ .ε CNλ
(2.18)
Onde ∈λ é denominada emissividade.
Substituindo essa equação em 2.16, temos que a emitância radiante total de um corpo cinza (ECC) é:
E =∈ σT 4
(2.19)
Na tabela 2.1 são apresentados alguns valores de emissividade:
Material
Concreto
Vidro
Gelo
PVC
Neve
∈
0,92 – 0,97
0,92
0,97
0,91 – 0,93
0,80
Material
Papel preto
Papel verde
Papel branco
Areia
Pele humana
∈
0,90
0,85
0,68
0,90
0,98
Material
Solo seco
Solo saturado
Água
Alumínio anodizado
Alumínio polido
∈
0,92
0,95
0,95
0,77
0,05
Tabela 2.1 – Alguns valores de emissividade
ER 2.5. Um planeta de raio Rp realiza uma órbita em torno de uma estrela de raio RE. Esta estrela é
isotérmica à temperatura TE e emite radiação como um corpo negro. Qual é o fluxo total emitido por essa
estrela ?
Resolução
Do ER 2.1 vimos que: E =
F
F
⇒ Eo =
⇒ F = E o 4πR 2
2
ΔA
4πR
Da equação 2.16, vimos que: E = σT 4 .
Portanto, para essa estrela, temos: F = σTE4 4πR 2E
ER 2.6. A órbita do planeta em torno da estrela do exercício 2.5 é excêntrica a ponto da distância que os
separa sofrer variações de cerca de 20% em relação à média. Avalie a irradiância incidente no planeta nos
pontos de máximo e mínimo afastamento.
Universidade Federal de Itajubá – Instituto de Recursos Naturais
14
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
Resolução
E mín =
F
4πR 2E σTE4
R 2E σTE4
=
=
1,56
ΔA 4π(0,8d) 2
d2
E máx =
F
4πR 2E σTE4
R 2E σTE4
=
=
0,
69
ΔA 4π(1, 2d) 2
d2
Ou seja, Emín = 1,56 Emédia, enquanto Emáx = 0,69 Emédia
2.5.5. Lei de Beer-Bouguer-Lambert (August Beer, Pierre Bouguer, Johann Heinrich Lambert)
A lei de Beer é assim definida: “Um feixe monocromático de radiação sofre uma atenuação
exponencial ao atravessar um meio homogêneo.” Matematicamente, a mesma pode ser rescrita como:
I λ = I oλ e − k λ s
(2.20)
Onde kλ é o coeficiente espectral de extinção e s é o caminho óptico.
A lei de Beer, expressa em 2.20, é representada na figura 2.8.
Figura 2.8 – Representação para a Lei de Beer
No entanto, o fluxo de radiação pode incidir de maneira inclinada sobre a superfície. Assim, se
redesenharmos a figura 2.8 levando em consideração o fluxo de radiação, temos:
Universidade Federal de Itajubá – Instituto de Recursos Naturais
15
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
Figura 2.9 – Fluxo inclinado na superfície
Sobre a superfície, o fluxo incidente é dado por:
IN =
F
A1
IN é denominada irradiância normal, ou seja, perpendicular à superfície.
No entanto, o fluxo atinge perpendicularmente uma determinada área A2, cuja irradiância é dada por:
I=
F
A2
Como o fluxo é o mesmo, pode-se escrever que:
I = IN
A1
A2
Como a relação A1/A2 é o cosseno do ângulo ζ,, então escreve-se que:
I = I N cos ζ
(2.21)
2.6. ESTIMATIVAS DE IRRADIÂNCIA SOLAR DIRETA, GLOBAL E DIFUSA
A radiação solar que incide no topo da atmosfera varia basicamente com a latitude e o tempo, isto é,
a época do ano e a hora do dia. Ao entrar na atmosfera parte da radiação solar interage com os elementos
presentes e parte atinge a superfície sem que haja interações. Assim, denomina-se de Radiação Direta a parte
da energia solar que atravessa a atmosfera e não sofre interações com o volume de matéria, chegando
“diretamente” à superfície. Portanto, a densidade de fluxo deste tipo de radiação é chamada de irradiância
solar direta (ID). A Radiação Difusa é a parte da radiação solar que sofreu algum tipo de interação com o
volume de matéria e atinge a superfície vinda de outras direções que não aquela do sol. Relativa a este fluxo,
Universidade Federal de Itajubá – Instituto de Recursos Naturais
16
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
denomina-se irradiância solar difusa (Id). A soma de ambas irradiâncias é denominada irradiância total (I).
Assim, tem-se:
I = I D + Id
(2.22)
Para uma superfície horizontal, a equação 2.22 pode ser rescrita como:
I = I N cos ζ + Id
(2.23)
Onde IN é a irradiância normal à superfície e ζ é a distância zenital do sol.
Uma vez conhecidas as componentes (direta, difusa e global) da radiação, vamos estudar algumas
técnicas empíricas (ou semi-empíricas) para estimativa destas componentes:
2.6.1. Irradiância solar no topo da atmosfera
A irradiância instantânea (Io) sobre uma superfície horizontal no topo da atmosfera é dada por:
2
⎛d⎞
Io = S ⎜ ⎟ cos ζ
⎝d⎠
(2.24)
Onde S é a constante solar, definida como a irradiância solar normal a uma distância média Terra-Sol na
2
⎛d⎞
ausência de atmosfera. Seu valor é de, aproximadamente, 1367 Wm . O valor de ⎜ ⎟ é dado pela equação
⎝d⎠
-2
1.1 e ζ é a distância zenital do sol.
No entanto, para muitos estudos, é de interesse determinar a quantidade total de radiação incidente
ao longo de um dia. Ou seja, a irradiância solar diária (ou a dose) sobre a superfície. Para tanto, basta
usarmos a equação 2.7:
tp
2
⎛d⎞
Do = ∫ S ⎜ ⎟ cos ζdt
d⎠
tn ⎝
Onde tn e tp são os instantes de nascer e do pôr do sol, respectivamente.
Combinando as equações 2.23 e 1.13, temos:
Universidade Federal de Itajubá – Instituto de Recursos Naturais
(2.25)
17
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
2
tp
⎛d⎞
Do = ∫ S ⎜ ⎟ ( senϕ senδ + cos ϕ cos δ cos H ) dt
d⎠
tn ⎝
(2.26)
Algumas aproximações podem ser feitas em 2.26. Em um único dia, a distância Terra-Sol (d) e a declinação
(δ) são praticamente constantes. Portanto, como a latitude também é constante, podem “sair” da integral. Isto
é:
⎛d⎞
Do = S ⎜ ⎟
⎝d⎠
tp
tp
⎛
⎞
⎜ senϕ senδ ∫ dt + cos ϕ cosδ ∫ cos Hdt ⎟
⎜
⎟
tn
tn
⎝
⎠
2
(2.27)
Para facilitar a integração de cosH, podemos relacionar o tempo (t) com o ângulo horário (H),
através da velocidade angular de rotação da Terra (ω), já que:
dh
=ω
dt
⇒
dt =
1
dh
ω
(2.28)
Então, 2.27 pode ser rescrita como:
2
+H
+H
⎞
S⎛d⎞ ⎛
Do = ⎜ ⎟ ⎜ senϕ senδ ∫ dh + cos ϕ cosδ ∫ cos Hdh ⎟
ω⎝ d ⎠ ⎝
−H
−H
⎠
(2.29)
Integrando e substituindo os valores de S e de ω temos:
2
⎛d⎞
Do = 37, 6 ⎜ ⎟ ( H senϕ senδ + cos ϕ cosδ senH )
⎝d⎠
(2.30)
Sendo H em radianos e Do em MJ/m2.
→ Tente calcular a irradiância solar diária no topo da atmosfera sobre Itajubá (22,41°S; 45,44°W) para hoje.
2.6.2. Irradiância global à superfície
Normalmente os valores de irradiâncias (global, direta ou difusa) são obtidos através de medidas
realizadas por instrumentos instalados em superfície ou a bordo de satélites. Veremos mais detalhes sobre
instrumentação meteorológica em um tópico especial. No entanto, é possível avaliar, de uma maneira
aproximada, as irradiâncias numa determinada localidade onde não haja instrumentação adequada.
Universidade Federal de Itajubá – Instituto de Recursos Naturais
18
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
Dentre muitas aproximações empíricas existentes na literatura, a mais difundida é aquela que utiliza
a técnica estatística dos mínimos quadrados. Neste caso, a irradiância global é representada pela seguinte
equação:
n⎞
⎛
I = Io ⎜ a + b ⎟
N⎠
⎝
(2.31)
Onde, os termos a e b são determinados empiricamente através de regressão linear de medidas prévias
realizadas em uma determinada localidade; n é a duração do brilho solar observado e N a duração
astronômica do período diurno (n e N em horas).
Para determinar a e b, rescreve-se a equação 2.31 da seguinte forma:
Y = a + bX
(2.32)
Com Y = I/Io e X = n/N. Podemos então escrever o seguinte sistema de equações:
⎧⎪∑ Y = K1a + b∑ X
⎨
⎪⎩∑ Y = K 2 a + b∑ X
(2.33)
Onde o termo K1 e K2 indicam o número de pares de valores observados (X,Y) usados. O ajuste da
reta é feito pelo coeficiente de regressão linear (r). O valor de r varia de –1 ≤ r ≤ +1 e a reta é tão melhor
quanto r se aproxima de 1. O coeficiente r é dado por:
r=
⎡⎣ K ∑ XY − ∑ X ∑ Y ⎤⎦
⎡ K X 2 − ( X )2 ⎤ ⎡ K Y 2 − ( Y )2 ⎤
∑ ⎦⎥ ⎣⎢ ∑
∑ ⎦⎥
⎣⎢ ∑
{
}
(2.34)
Varejão-Silva (2005) destacam algumas observações importantes para uma boa estimativa. Quando
existem muitos pares de valores (I, n) diários, é conveniente separá-los em conjuntos relacionados com a
quantidade de nebulosidade. Desta forma, obter-se-á um coeficiente de regressão para cada caso e os
resultados, por conseqüência, se tornam mais representativos. Estudos mostram que quando há muita
nebulosidade (n pequeno), o ajuste tende a ser pior do que aquele observado para céu claro (n grande). Isso
ocorre, pois não há como um heliógrafo (sensor que registra o tempo de insolação) diferenciar situações de
nuvens que podem influenciar bastante na relação de radiação direta/difusa e, portanto, pode apontar
medidas semelhantes para diferentes condições de nebulosidade.
Universidade Federal de Itajubá – Instituto de Recursos Naturais
19
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
2.6.3. Irradiância solar direta à superfície
Também existem diversos métodos empíricos para se determinar o valor de irradiância solar direta.
Vianello e Alves (1991) apresentam a relação de Brooks para irradiância direta normal (IN) sob condições de
céu limpo:
2
⎛d⎞
IN = S⎜ ⎟ τ
⎝d⎠
(2.35)
Onde τ é a transmitância atmosférica dada por:
0,75
0,60
⎡
⎤
⎛ pm ⎞
⎛ Wm ⎞
0,90
τ = exp ⎢ −0, 089 ⎜
⎟ − 0,174 ⎜
⎟ − 0, 083(dm) ⎥
⎝ 1013 ⎠
⎝ 20 ⎠
⎢⎣
⎥⎦
(2.36)
Em 2.36, p é a pressão atmosférica (em hPa) e d é a espessura óptica (parâmetro de atenuação) relacionada
aos aerossóis (adimensional). O valor de d depende de quão poluída é a região. Por exemplo, uma localidade
urbana apresenta d ~ 0,5 em condições poluídas. m é a massa óptica (também adimensional) dada por:
m = 35 1 − cos 2 ζ
(2.37)
Repare que m varia de 1 (quando ζ = 0° → sol no zênite) até 35 (quando ζ = 90° → sol no horizonte).
E W é a quantidade de água precipitável na atmosfera, na direção do zênite, (em mm), dada pela fórmula de
Hann:
W = 2,5e
(2.38)
Onde e é a pressão de vapor em hPa. Veremos mais sobre esta fórmula no próximo capítulo.
Um exemplo de modelo mais complexo e preciso para cálculos de irradiâncias diretas e difusas pode
ser visto em http://rredc.nrel.gov/solar/pubs/spectral/model/spectral_model_index.html.
2.6.4. Irradiância solar global sobre superfícies inclinadas
No caso de superfícies inclinadas, o valor instantâneo da irradiância global para céu claro é dado por:
I = I N cos θ + Id cos 2 (α / 2) + R(I N cos θ + Id )sen 2 (α / 2)
Universidade Federal de Itajubá – Instituto de Recursos Naturais
(2.39)
20
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
Onde α é a inclinação da superfície e R é a refletância (albedo) da superfície inclinada. O termo cos2(α/2)
corresponde à fração do céu vista da superfície inclinada. θ é o ângulo de incidência dos ângulos solares
diretos. A figura 2.10 auxilia esquematiza o fenômeno.
Figura 2.10 – Irradiância em plano inclinado
O cosseno de θ é calculado através das informações geográficas da localidade e da inclinação da superfície:
cos θ = cos H(cos ϕ cos δ cos α + senα cos A cos δsenϕ) +
+senH senα senA cos δ + senϕsenδ cos α − senα cos A cos δsenϕ
(2.40)
2.7. ESTIMATIVAS DE RADIAÇÃO DE ONDA LONGA
Tanto a Terra, quanto a atmosfera emitem radiação, aproximadamente, como um corpo negro.
Portanto, se as temperaturas da Terra e da atmosfera são conhecidas, é possível estimar os fluxos emitidos
através da equação de Stefan-Boltmann (2.14). Sabemos também, pela Lei de Wien (2.13), que, devido às
suas baixas temperaturas, a emissão máxima do sistema Terra-atmosfera se dá na faixa do infravermelho
(ondas longas). Como a atmosfera apresenta uma grande variabilidade de seus componentes como o vapor
d’água, gotas de água e cristais de gelo, é muito difícil determinar o comportamento radiativo deste sistema.
De qualquer forma, existem algumas equações empíricas que nos ajudam a estimar esses fluxos de
radiação. O saldo de radiação de onda longa (E) medido à superfície é dado pela diferença entre o que chega
da atmosfera (EA) e o que é emitido pela superfície (ES):
E = E A − ES
(2.41)
Em intervalos de tempo pequenos, o valor de E pode ser positivo, negativo, ou mesmo, nulo. Em intervalos
maiores, geralmente é negativo, já que a superfície emite mais radiação do que recebe da atmosfera. Apesar
dos erros grosseiros que possam acarretar, as fórmulas empíricas promovem resultados relativamente
Universidade Federal de Itajubá – Instituto de Recursos Naturais
21
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
confiáveis se aplicadas nas condições para as quais foram desenvolvidas. Dois exemplos destas fórmulas são
fornecidos por Varejão-Silva, 2005:
a) Fórmula de Brunt (1932)
E = −1440σT 4 (1 − a − b e)
(2.42)
Onde e é a pressão de vapor (em hPa) e T é a temperatura absoluta (em K). Os coeficientes a e b, valem
0,256 e 0,065, respectivamente. Em 1939, Brunt aperfeiçoou a equação 2.42 para condições de nebulosidade,
incluindo o parâmetro m para cobertura do céu (em décimos):
E = −1440σT 4 (c − d e)(1 − 0, 09m)
(2.43)
Onde c = 0,56 e d = 0,092.
b). Fórmula de Brunt-Pennman (1948)
Propõe-se a substituição do parâmetro m pelos parâmetros de insolação (n) e fotoperíodo (N) na
fórmula de Brunt e a equação passa a ser:
E = −1440σT 4 (c − d e)[1 − 0, 09(n / N)]
(2.44)
c) Fórmula de Swinbanck (1963)
Para dias de céu claro:
E = K(0,195σT 4 − 17, 09)
(2.45)
Com K = 1 para resultados em mW/cm2 ou K = 0,01433 para resultados em cal/cm2min
2.8. BALANÇO DE RADIAÇÃO
O balanço de radiação é dado pela diferença entre a energia recebida e a perdida, em ondas curtas e
longas, pela superfície, camada atmosférica ou, até mesmo, todo o planeta. Nesta seção veremos o balanço
de energia à superfície e o balanço no planeta, isto é, considerando todos os mecanismos de emissão,
espalhamento e absorção de radiação que ocorre entre a superfície, a atmosfera (gases, nuvens e aerossóis) e
o espaço.
Universidade Federal de Itajubá – Instituto de Recursos Naturais
22
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
2.8.1. Balanço de radiação à superfície
Para melhor compreensão do balanço de radiação em uma superfície, observemos a figura 2.11:
Figura 2.11 – Balanço de radiação em superfície
(R – Refletância da superfície; ID – Irradiância direta; Id – Irradiância difusa
ES – Emitância da superfície; EA – Emitância da atmosfera)
Da figura 2.11, vamos escrever os balanços de onda curta e onda longa:
BOC = I D + Id − R(I D + Id ) = I − RI = I(1 − R)
(2.46)
BOL = E A − ES
(2.47)
Então, o balanço à superfície (BS) é dado pela soma dos balanços de onda curta (BOC) e onda longa (BOL):
BS = I(1 − R) + (E A − ES )
(2.48)
Obs: Para o balanço de onda longa, Brunt propôs a seguinte relação:
BOL = 4,8989 × 10−9 T 4 (0, 09 e − 0,56) [ 0,1 + 0,9(n / N)]
(2.49)
2.8.2. Balanço de radiação no sistema Terra-atmosfera
O balanço de radiação envolvendo toda superfície e a atmosfera terrestre é bem complexo. Na figura
2.12 é apresentado um esquema dos percentuais de radiação absorvida, emitida e refletida pelo planeta e a
atmosfera. Considerando que a energia solar que chega no topo da atmosfera seja de 100 unidades quaisquer,
parte dela é absorvida pela atmosfera (19), parte refletida por nuvens (20) e parte é espalhada pela atmosfera
(6). Como a superfície reflete, em média, 4% da radiação que a atinge, então a energia absorvida pelo solo é
Universidade Federal de Itajubá – Instituto de Recursos Naturais
Disciplina: Fundamentos de Meteorologia (EAM-010) – Prof. Marcelo de Paula Corrêa – v.1.0.1
23
de 51 unidades. O albedo planetário, como se denomina a radiação refletida pelo sistema, é dado pela soma
dos termos espalhados pelas nuvens, pela atmosfera e pela reflexão da superfície, resultado em 30 unidades.
Figura 2.12 – balanço de radiação no sistema Terra-atmosfera
Quanto à onda longa, a superfície emite 117 unidades, das quais a maior parte é absorvida pela
atmosfera (111) e apenas uma pequena porção se perde para o espaço (6). A atmosfera, incluindo as nuvens,
também recebe energia das fontes de evaporação e convecção da superfície, tornando-se uma grande fonte de
emissão (160). Para a superfície a atmosfera emite 96 unidades, enquanto que para o espaço perdem-se 64
unidades. Obviamente, estes valores são aproximados e dependem de todos os fenômenos meteorológicos
que ocorrem na atmosfera terrestre.
Universidade Federal de Itajubá – Instituto de Recursos Naturais