CIRCUITO MAGNÉTICO

CIRCUITO MAGNÉTICO (introdução)
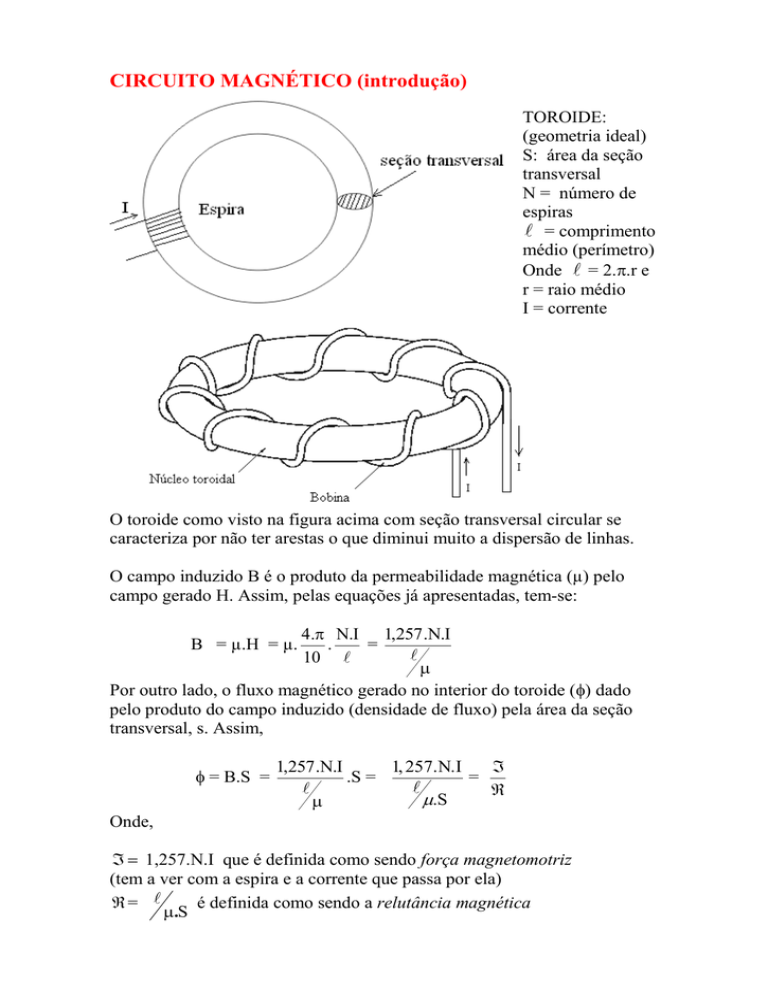
TOROIDE:
(geometria ideal)
S: área da seção
transversal
N = número de
espiras
 = comprimento
médio (perímetro)
Onde  = 2..r e
r = raio médio
I = corrente
O toroide como visto na figura acima com seção transversal circular se
caracteriza por não ter arestas o que diminui muito a dispersão de linhas.
O campo induzido B é o produto da permeabilidade magnética (µ) pelo
campo gerado H. Assim, pelas equações já apresentadas, tem-se:
4. N.I 1,257 .N.I
.
=

10 

Por outro lado, o fluxo magnético gerado no interior do toroide () dado
pelo produto do campo induzido (densidade de fluxo) pela área da seção
transversal, s. Assim,
B = µ.H = µ.
 = B.S =
1, 257.N.I
1,257 .N.I

.S =
=


m.S

Onde,
  1,257.N.I que é definida como sendo força magnetomotriz
(tem a ver com a espira e a corrente que passa por ela)
= 
é definida como sendo a relutância magnética
.S
(tem a ver com geometria do circuito e o seu material)
Assim pode-se escrever:
B
  Â.j =    xB.S = x  = H. 
 .S 

Esta expressão é conhecida como Lei de Hopkinson.
ANALOGIA COM CIRCUITO ELÉTRICO:
Podemos fazer uma analogia entre um circuito magnético e um circuito
elétrico, onde  seria a “voltagem” e  seria a “resistência” e fluxo , a
corrente.
Num circuito elétrico tem-se, pela lei de Kirchhoff das malhas, num
circuito série:
V = I.(R1 + R2 + ....RN)
O que dá no mesmo:
V = V1 + V2 + ....VN
Num circuito magnético, por seu lado, pela lei de Hopkinson, tem-se
analogamente:

+ Â2 + .... ÂN )
O que dá no mesmo:
  1 + 2 + ..... N
 N.I = H1.  1 + H2.  2 + .. + HN.  N
 1,257xN.I = H1.  1 + H2. 2 + .. + HN.  N
(MKS)
(CGS)
Para resolução, deve-se conhecer a permeabilidade de cada material
pela relação BXH, tabela ou pelas curvas de magnetização.
No circuito magnético abaixo, cada trecho do circuito tem um comprimento
 , uma área de seção transversal S e uma permeabilidade µ.
Dado o fluxo  que se deseja, divide-se pela área de cada trecho do circuito
para de determinar o campo induzido B que é a densidade de fluxo (B=/S)
Determina H para cada trecho pela tabela ou gráfico de magnetização.
O µ também é determinado pela tabela ou gráfico de magnetização.
Analogia entre o circuito elétrico e magnético:
Circuito elétrico
Circuito magnético
Corrente: I = V/R =
V

.S

=


.S
f.m.m: 
Voltagem: V
Resistência: R = 
Fluxo:  = 
.S
Condutividade: σ
Relutância:  = 
.S
Permeabilidade: µ
Comparação entre os sistemas MKS (SI) e CGS:
MKS
H = N.I/  (A.m-1)
CGS
H = (4./10). N.I/  A.cm-1 = Oe
B = µo.H = 4..10-7.H (ar) (Tesla)
B = H (ar) (Gauss)  G
 = N.I = H.  (A.e)
 = 1,257.N.I ; Gilbert
 = B.S (Weber)
 = B.S (linhas = Maxwel)
1 Oe  80 A.m-1
1 A.m-1 = 4..10-3 Oe