QUESTÃO 200056
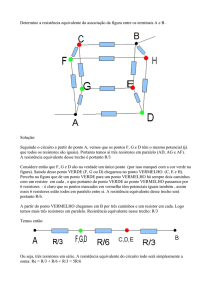
Determine a corrente que chega no capacitor do circuito esquematizado abaixo. Sabe-se que a
carga armazenada no capacitor é de 10nC.
3Ω
4Ω
6Ω
2Ω
4Ω
5Ω
2Ω
2nF
10V
5Ω
4Ω
2Ω
RESOLUÇÃO
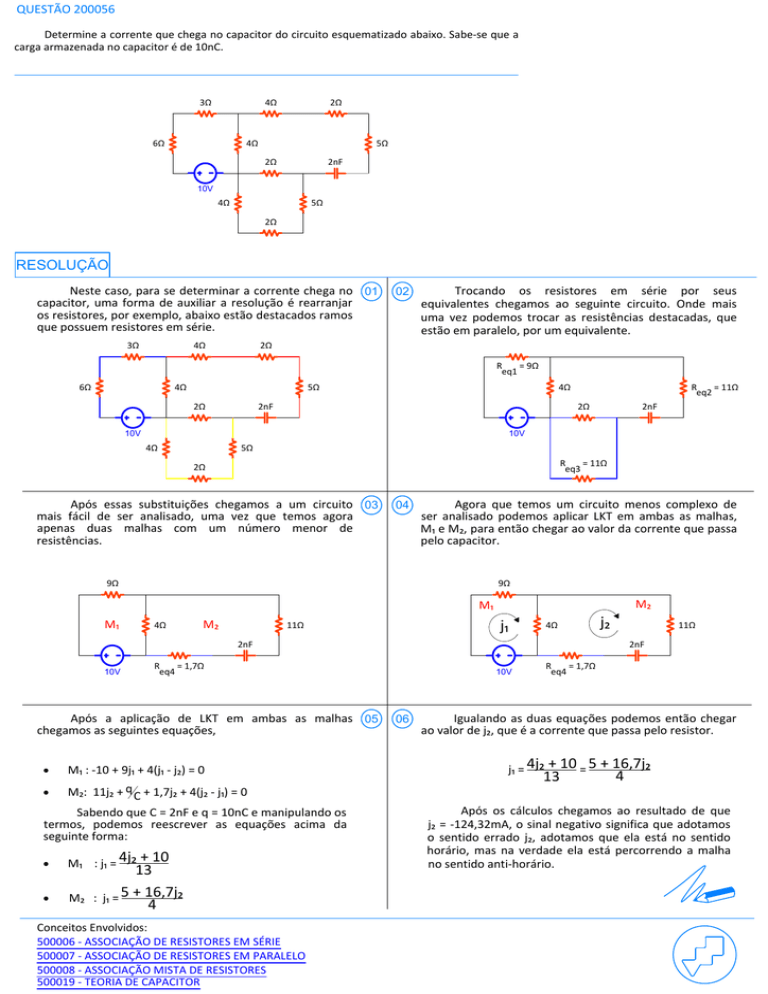
Neste caso, para se determinar a corrente chega no 01
capacitor, uma forma de auxiliar a resolução é rearranjar
os resistores, por exemplo, abaixo estão destacados ramos
que possuem resistores em série.
3Ω
4Ω
02
Trocando os resistores em série por seus
equivalentes chegamos ao seguinte circuito. Onde mais
uma vez podemos trocar as resistências destacadas, que
estão em paralelo, por um equivalente.
2Ω
R
= 9Ω
eq1
6Ω
4Ω
5Ω
2Ω
4Ω
2nF
R
= 11Ω
eq2
2Ω
10V
2nF
10V
4Ω
5Ω
R
= 11Ω
eq3
2Ω
Após essas substituições chegamos a um circuito 03
mais fácil de ser analisado, uma vez que temos agora
apenas duas malhas com um número menor de
resistências.
04
Agora que temos um circuito menos complexo de
ser analisado podemos aplicar LKT em ambas as malhas,
M₁ e M₂, para então chegar ao valor da corrente que passa
pelo capacitor.
9Ω
9Ω
M₂
M₁
M₁
4Ω
M₂
j₁
11Ω
4Ω
j₂
11Ω
2nF
10V
R
= 1,7Ω
eq4
Após a aplicação de LKT em ambas as malhas 05
chegamos as seguintes equações,
·
M₁ : -10 + 9j₁ + 4(j₁ - j₂) = 0
·
M₂: 11j₂ + q C + 1,7j₂ + 4(j₂ - j₁) = 0
Sabendo que C = 2nF e q = 10nC e manipulando os
termos, podemos reescrever as equações acima da
seguinte forma:
·
·
2nF
M₁ : j₁ = 4j₂ + 10
13
M₂ : j₁ = 5 + 16,7j₂
4
Conceitos Envolvidos:
500006 - ASSOCIAÇÃO DE RESISTORES EM SÉRIE
500007 - ASSOCIAÇÃO DE RESISTORES EM PARALELO
500008 - ASSOCIAÇÃO MISTA DE RESISTORES
500019 - TEORIA DE CAPACITOR
10V
06
R
= 1,7Ω
eq4
Igualando as duas equações podemos então chegar
ao valor de j₂, que é a corrente que passa pelo resistor.
j₁ = 4j₂ + 10 = 5 + 16,7j₂
13
4
Após os cálculos chegamos ao resultado de que
j₂ = -124,32mA, o sinal negativo significa que adotamos
o sentido errado j₂, adotamos que ela está no sentido
horário, mas na verdade ela está percorrendo a malha
no sentido anti-horário.