Solução

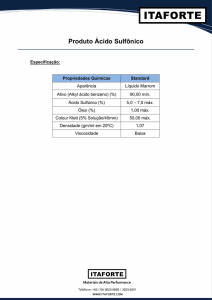
www.fisicaexe.com.br
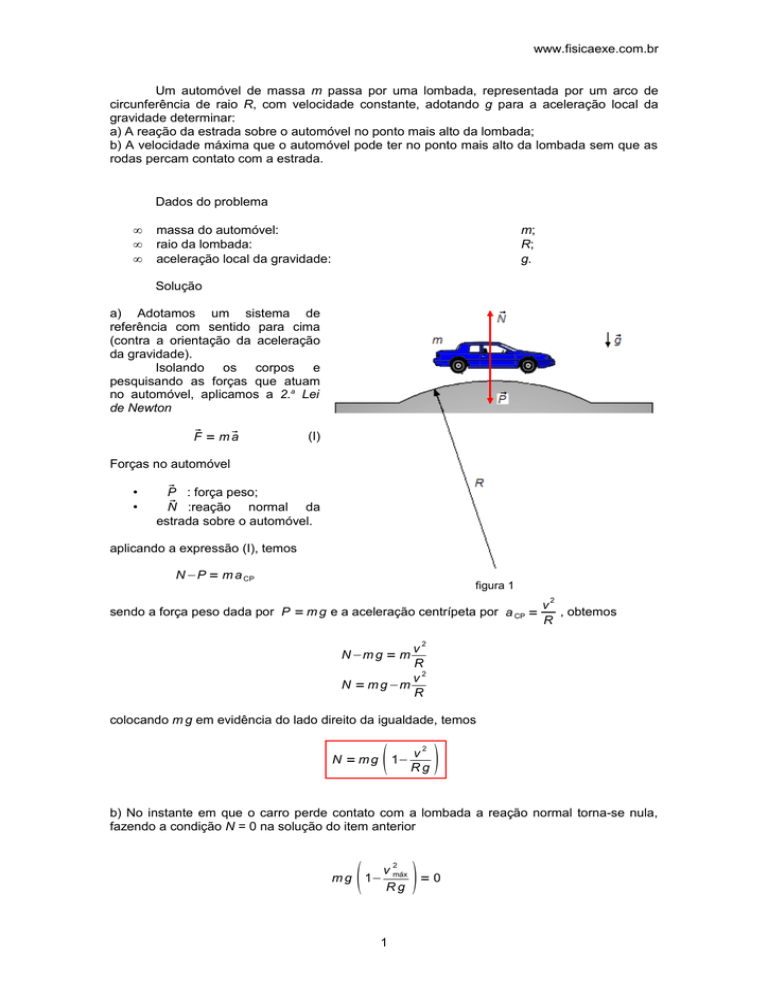
Um automóvel de massa m passa por uma lombada, representada por um arco de
circunferência de raio R, com velocidade constante, adotando g para a aceleração local da
gravidade determinar:
a) A reação da estrada sobre o automóvel no ponto mais alto da lombada;
b) A velocidade máxima que o automóvel pode ter no ponto mais alto da lombada sem que as
rodas percam contato com a estrada.
Dados do problema
•
•
•
massa do automóvel:
raio da lombada:
aceleração local da gravidade:
m;
R;
g.
Solução
a) Adotamos um sistema de
referência com sentido para cima
(contra a orientação da aceleração
da gravidade).
Isolando os corpos e
pesquisando as forças que atuam
no automóvel, aplicamos a 2.a Lei
de Newton
 = m
F
a
(I)
Forças no automóvel
•
•
 : força peso;
P
 :reação normal da
N
estrada sobre o automóvel.
aplicando a expressão (I), temos
N −P = m a CP
figura 1
2
sendo a força peso dada por P = m g e a aceleração centrípeta por a CP =
v
, obtemos
R
2
v
R
v2
N = m g −m
R
N −m g = m
colocando m g em evidência do lado direito da igualdade, temos

N = mg
2
1−
v
Rg

b) No instante em que o carro perde contato com a lombada a reação normal torna-se nula,
fazendo a condição N = 0 na solução do item anterior
mg

2
1−

v máx
=0
Rg
1
www.fisicaexe.com.br
2
v máx
=0
R
2
v
m g = m máx
R
m g −m
simplificando a massa m de ambos os lados da igualdade
2
v máx
R
2
v máx = R g
g=
v máx =  R g
2