Aluno: Ricardo Paleari da Silva Orientador: Edson - MAT-UFG

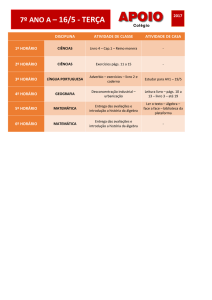
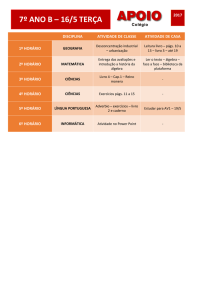
Álgebras Hereditárias
1
Silva
Aluno: Ricardo Paleari da
2
Orientador: Edson Ribeiro Alvares
1
2
[email protected]
[email protected]
http://www.mat.ufpr.br/∼pet/
Resumo
Existe uma forma mais visível de representar álgebras de dimensão finita. Isso é feito por meio de grafos orientados. Apresentamos abaixo como fazer
isso dada uma álgebra de matrizes. Estudamos também um caso particular de álgebra, chamada álgebra hereditária.
1 Estruturas Algébricas
As estruturas mais importantes tratadas nessa pesquisa são as Álgebras e
os Módulos. A razão disto é a busca de encontrar uma forma de "representar" certos tipos de álgebras de uma forma mais "visível" e acessível,
principalmente por meio de grafos orientados. Dada essa representação, é
possível estudar os módulos sobre essa álgebra e extrair algumas de suas
propriedades e podendo assim, de alguma forma, caracterizar as álgebras
estudadas.
Definição 1. Seja K um corpo. Uma K-álgebra é um anel Λ com unidade
que possui estrutura de K-espaço vetorial de tal forma que:
α(a · b) = (α · a)b = a(α · b) = (a · b)α
para quaisquer a, b ∈ Λ e α ∈ K.
Definição 2. Seja Λ uma K-álgebra. Diremos que um conjunto não vazio
M é um Λ-Módulo à esquerda (analogamente a direita) se M é um grupo
abeliano com + e é tal que a multiplicação por escalares em Λ satisfaz:
1)
2)
3)
4)
(ab)x = a(bx)
a(x + y) = ax + ay
(a + b)x = ax + bx
1.x = x
Para todos os x, y ∈ M e a, b ∈ Λ.
Exemplo 1. Denotaremos por Mn(K) o conjunto das matrizes n × n com
elementos num corpo K. Este conjunto forma uma K-álgebra não comutativa (com o produto). Chamamos esta álgebra de álgebra de matrizes.
No caso n = 2 por exemplo, podemos denotar esta álgebra com a forma
abaixo:
µ
¶
K K
M2 =
K K
Uma forma de relacionar as estruturas de álgebras e seus módulos foi
adquirida pelos matemáticos Krull e Schmidt que enunciaram o seguinte
teorema:
Teorema 1. Seja Λ uma K-Álgebra de dimensão finita. Então todo módulo
M a esquerda sobre Λ e finitamente gerado possui uma única decomposição em uma soma direta de um número finito de módulos indecomponíveis
finitamente gerados. Ou seja:
M∼
= M1 ⊕ M2 ⊕ ... ⊕ Mn
Se M ∼
= N1 ⊕ N2 ⊕ ... ⊕ Nr é outra decomposição em indecomponíveis,
então r = n e existe uma permutação de índices σ tal que Mi ∼
= Nσ(i)
para cada i.
Como uma K-Álgebra Λ pode ser vista como um Λ-Módulo, segue do
teorema acima que se Λ é uma K-Álgebra de dimensão finita, então podemos decompor Λ como uma soma direta de módulos indecomponíveis:
Λ∼
= P1 ⊕ P2 ⊕ ... ⊕ Pn
Com isso, decompondo a unidade 1 de Λ temos:
1 = e1 + e2 + ... + en
Com ei ∈ Pi. Temos então o seguinte teorema:
Teorema 2. O conjunto {e1, e2, ..., en} como acima forma um sistema:
1. Completo: 1 = e1 + e2 + ... + en;
2. de Idempotentes: e2i = ei, i = 1, ..., n;
3. Ortogonais: ei · ej = 0 se i 6= j.
4. e Primitivos: se ei = f + g, com f, g idempotentes ortogonais, então
f = 0 ou g = 0
Com esse resultado, podemos verificar quando uma álgebra é indecomponível conhecendo seus idempotentes com o seguinte resultado:
Teorema 3. Seja Λ uma K-Álgebra. Λ é indecomponível se, e somente se,
seus únicos idempotentes centrais são 0 e 1.
Se {e1, ..., en} é um sistema completo, de idempotentes ortogonais e primitivos de uma K-álgebra Λ de dimensão finita então temos uma forma de
decompor esta álgebra em soma direta de indecomponíveis com relação
aos seus idempotentes na forma: Λ ∼
= Λe1 ⊕ Λe2 ⊕ ... ⊕ Λen
Exemplo 2. Seja Λ a álgebra das matrizes de ordem 2 com elementos num
corpo K.
e1 · e1 = e1, e3 · β = β, β · α = βα.
A base B da álgebra KC é o conjunto:
Λ=
µ
K K
K K
¶
B = {e1, e2, e3, α, β, βα}
Os subconjuntos de Λ dados por:
¶
¶
µ
µ
0 K
K 0
, I2 =
I1 =
0 K
K 0
São ideais a esquerda de Λ.
Aqui temos: I1 + I2 = {x1 + x2, x1 ∈ I1 e y ∈ I2} = Λ e como
I1 ∩ I2 = {0}, onde 0 indica a matriz nula de ordem 2, segue que
Λ = I1 ⊕ I2. Por verificação direta dos axiomas, é possível concluir
que I1 e I2 são Λ-Módulos a esquerda de Λ. Λ = I1 ⊕ I2 é uma decomposição de Λ em módulos a esquerda sobre Λ.
Um conjunto completo, de idempotentes ortogonais e primitivos para Λ
é dado por:
½
µ
¶
µ
¶¾
1 0
0 0
B = e11 =
, e22 =
0 0
0 1
Pois e11 + e22 = I (I é a matriz identidade de ordem 2), e211 = e11,
e222 = e22 e e11 · e22 = 0. Como foi mencionado, podemos decompor Λ na
forma: Λ = Λe11 ⊕ Λe22. Veja que Λe11 = I1 e Λe22 = I2.
Um objeto muito importante para o estudo das álgebras de dimensão
finita e suas representações em forma de grafos orientados é o ideal denominado radical da álgebra definido abaixo:
Definição 3. O radical de uma K-Álgebra Λ é a interseção de todos os
ideais maximais a direita de Λ.
2 Álgebras de Caminhos
Começamos agora a comentar a relação entre uma álgebra de dimensão
finita e uma álgebra construída a partir de um grafo com a seguinte definição:
Definição 4. Uma aljava C é um grafo orientado, conexo e finito. Mas
precisamente, composto por um conjunto finito C0 de elementos chamados "vértices"de C e um outro conjunto C1 de elementos chamados "flechas"de C. Para cada flecha fazemos uma associação ao seu vértice inicial e seu vértice final. Um caminho dirigido de longitude n de i a j em
uma aljava C é uma sucessão de vértices e flechas de C.
Um caminho dirigido é denotado da seguinte forma: (j|an, ..., a1|i).
Sendo que, para m > 1, i o começo de a1, o final de a1 é o início de
a2, o final de a2 é o começo de a3 e assim por diante até que seja j o final
de an. Se m = 0 temos que i = j e podemos escrever τi = {i||i}, este
tipo de caminho é chamado caminho trivial.
Se K é um corpo, definimos um K-espaço vetorial sobre uma aljava
C de forma que sua base seja dada pelo conjunto de todos os vértices
(incluindo os triviais), flechas e caminhos dirigidos de C. Esse espaço
vetorial é denotado por KC. Para que tenhamos uma estrutura de álgebra
sobre KC vamos definir o produto de dois elementos de KC da seguinte
forma:
Se γ = (p|bmbm−1...b1|h) e δ = (j|anan−1...a1|i) são caminhos dirigidos em KC então:
½
(p|bmbm−1...b1anan−1...a1|i) , se h = j
γ·δ =
0
, se h 6= j
Desta forma, como a multiplicação foi definida nos elementos da base de
KC, podemos estender por linearidade esta definição a todos os elementos de KC obtendo assim uma estrutura de K-Álgebra para KC. Note
que o produto definido acima é diferente de 0 quando o final de δ coincide
com o começo de γ. Pode-se verificar que o elemento unidade dessa álgebra é dado por pela soma de todos os caminhos triviais de KC, ou seja,
|C
P0|
1=
τi .
Com isso, temos algumas propriedades que vem como consequência da
construção dessa álgebra (chamada Álgebra de Caminhos):
1. Seja S = {τi, i ∈ C0} o conjunto de todos os caminhos triviais de uma
álgebra de caminhos KC. Então S é um sistema completo de idempotentes ortogonais e primitivos.
2. Se C é uma aljava finita, então a álgebra KC é de dimensão finita se, e
somente se, C não possui ciclos orientados.
3. KC é uma álgebra indecomponível.
4. O radical de KC coincide com o ideal de gerado pelas flechas e produtos de flechas de KC quando C não possui ciclos dirigidos.
Exemplo 4. Seja Λ a sub-álgebra das matrizes da forma:


K 0 0
Λ = K K 0 
K K K
Neste caso o radical de Λ é a sub-álgebra das matrizes da forma:


0 0 0
rad (Λ) =  K 0 0 
K K 0
Temos que se x pertence ao quociente do radical de Λ pelo ideal rad2(Λ)
então x é da forma:


0 0 0
x =  K 0 0  + rad2 (Λ)
0 K 0
¤
£
2
O número dim ej rad(Λ)/rad (Λ)ei indica o número de flechas de ligam o vértice i ao vértice j na aljava C.
Nesse caso temos:
£
¤
2
dim £e1rad(Λ)/rad (Λ)ek¤ = 0 , k = 1, 2, 3.
dim £e2rad(Λ)/rad2(Λ)e1¤ = 1
dim e3rad(Λ)/rad2(Λ)e2 = 1
Então temos o grafo que representa a álgebra Λ:
•
1
α
/
•
2
β
/
•
3
3 Conclusão
Cada tipo de álgebra tem sua importância dependendo da área em que
estamos trabalhando. Dentre esse conjunto de álgebras podemos citar as
álgebras de Lie, álgebras de Nakayama, álgebras seriais, incidência, entre
outras. Uma delas, chamada Álgebra Hereditária, tem uma importância
na área de teoria de representações. Essas álgebras estão envolvidas com
propriedades das categorias dos módulos sobre essa álgebra. Sendo possível assim estudar seus módulos injetivos, projetivos e indecomponíveis.
Definição 5. Seja Λ uma álgebra. Dizemos que Λ é uma álgebra Hereditária se todo sub-módulo de módulo projetivo é projetivo.
Obs: P é dito módulo projetivo quando é somando direto de um M
módulo livre (módulo que possui base).
O teorema abaixo mostra a relação entre as álgebras hereditárias e uma
álgebra de caminhos, mostrando que existe uma visualização muito simples de como seria uma álgebra hereditária a respeito do seu grafo:
Teorema 4. : Uma álgebra Λ é hereditária se, e somente se, Λ ∼
= KC
onde C para alguma aljava C, onde C não possui ciclos dirigidos.
Nossa expectativa agora é estudar as propriedades dos módulos sobre
uma álgebra hereditária olhando para sua representação em forma de aljava, procurando estabelecer uma tradução das propriedades dadas numa
álgebra para sua forma de aljava.
i=1
Exemplo 3. Seja C a aljava abaixo:
•
1
α
/
•
2
β
/
•
3
Referências
[1] Cibils, C. Larrión, F. Salmerónn, L. Métodos Diagramáticos en teoría
de representaciones UNAM, México 1982.
Alguns Produtos em KC:
[2] Assem, Ibrahim; Simson, Daniel e Skowronski, Andrzej: Elements of
the Representation Theory of Associative Algebras. London Mathematical Society Student Texts 65 2005.
e1 · e2 = 0, e1 · α = α, α · β = 0
[3] Hoffman, Kenneth & Kunze, Ray Algebra Linear. 2o Edição. Livros
Técnicos e Científicos. Rio de Janeiro, 1979.