Preliminares

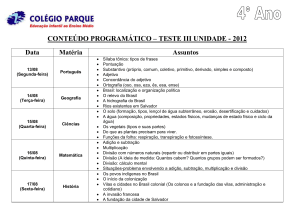
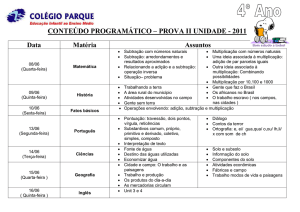
Capítulo 1
Preliminares*
OS CONJUNTOS DE NÚMEROS USADOS EM ÁLGEBRA
São, em geral, subconjuntos de R, o conjunto dos números reais.
Números naturais N
São os números empregados em processos de contagem, p. ex., 1, 2, 3, 4,...
Inteiros Z
Os números para contagem, acrescidos de seus opostos e 0, p. ex., 0, 1, 2, 3,... 1, 2, 3,...
Números racionais Q
O conjunto de todos os números que podem ser escritos como quocientes a/b, b 0, sendo a e b inteiros, p. ex.,
3/17; 10/3; 5,13;...
Números irracionais H
Todos os números reais que não são racionais, p. ex.,
Exemplo 1.1 O número 5 é elemento dos conjuntos Z, Q e R. O número 156,73 é um elemento dos conjuntos
Q e R. O número 5 é pertencente aos conjuntos H e R.
AXIOMAS PARA O SISTEMA DOS NÚMEROS REAIS
Há duas operações fundamentais, adição e multiplicação, que apresentam as seguintes propriedades (a, b e c são
números reais arbitrários):
Leis de fechamento
A soma a b e o produto a b ou ab são números reais únicos.
Leis de comutatividade
a b b a: a ordem é irrelevante na adição.
ab ba: a ordem é irrelevante na multiplicação.
* N. de T.: É importante frisar que as noções apresentadas neste livro são de caráter intuitivo, ou seja, não formal, uma vez que
a presente obra trata de pré-cálculo e não de análise matemática ou fundamentos da matemática.
Livro_Safier.indb 1
14/06/11 16:59
2
PRÉ-CÁLCULO
Leis associativas
a (b c) (a b) c: o agrupamento* é irrelevante em adições repetidas.
a(bc) (ab)c: o agrupamento é irrelevante em multiplicações repetidas.
Nota: (removendo parênteses): Uma vez que a (b c) (a b) c, a b c pode ser escrito significando
qualquer um dos lados da igualdade.
Analogamente, já que a(bc) (ab)c, abc corresponde a qualquer um dos lados da igualdade.
Leis distributivas
a(b c) ab ac; também (a b)c ac bc: multiplicação é distributiva em relação à adição.
Leis de identidade
Existe um único número 0 com a propriedade de que 0 a a 0 a.
Existe um único número 1 com a propriedade de que 1 a a 1 a.
Leis de inverso
Para qualquer número real a, existe um real a, tal que a (a) (a) a 0.
Para qualquer real a diferente de zero, existe um número real a1, tal que aa1 a1a 1.
a é chamado de inverso aditivo ou negativo de a.
a1 é chamado de inverso multiplicativo ou recíproco de a.
Exemplo 1.2
Leis associativa e comutativa. Simplifique (3 x) 5.
Exemplo 1.3 Distributividade dupla. Mostre que (a b)(c d) ac ad bc bd.
LEIS DE FATOR ZERO
1. Para cada número real a, a 0 0.
2. Se ab 0, então a 0 ou b 0.
LEIS PARA OS NEGATIVOS
1.
2.
3.
4.
(a) a
(a)(b) ab
ab (a)b a(b) (a)(b)
(1)a a
SUBTRAÇÃO E DIVISÃO
Definição de subtração:
Definição de divisão:
a b a (b)
. Desse modo,
Nota: Uma vez que 0 não admite inverso multiplicativo, a 0 não é definido.
* N. de T.: A expressão “agrupamento” se refere a termos, fatores ou expressões em geral que se encontram entre parênteses,
colchetes ou chaves.
Livro_Safier.indb 2
14/06/11 16:59
CAPÍTULO 1 • PRELIMINARES
3
LEIS PARA QUOCIENTES
1.
2.
3.
4.
se, e somente se,
para qualquer k real não nulo. (Princípio fundamental de frações)
PROPRIEDADES DE ORDEM
Os números reais positivos, denotados por R, são um subconjunto dos números reais e apresentam as seguintes
propriedades:
1. Se a e b estão em R, então a b e ab também estão.
2. Para cada número real a, ou a pertence a R, ou a é zero, ou a está em R.
Se a está em R, a é dito positivo; se a é elemento de R, a é chamado de negativo.
O número a é menor que b e escrevemos a b, se b a é positivo. Logo, b é maior que a e escrevemos b a.
Se a é menor ou igual a b, isso é representado por a b. Logo, b é maior ou igual a a, e escrevemos isso como b a.
Exemplo 1.4
3 5 porque 5 3 2 é positivo. 5 3 porque 3(5) 8 é positivo.
O que se segue pode ser deduzido conforme as definições acima:
1. a 0 se, e somente se, a é positivo.
2. Se a 0, então a2 0.
3. Se a b, então a c b c.
4. Se
, então
5. Para qualquer número real a, ou a 0, ou a 0, ou a 0.
6. Se a b e b c, então a c.
A RETA REAL
Números reais podem ser representados por pontos em uma reta l, tal que a cada número real a corresponda exatamente a um ponto sobre l, e reciprocamente.
Exemplo 1.5
sobre uma reta real.
Represente o conjunto
Figura 1-1
VALOR ABSOLUTO DE UM NÚMERO
O valor absoluto de um número real a, representado por | a |, é definido como:
Livro_Safier.indb 3
14/06/11 16:59
4
PRÉ-CÁLCULO
NÚMEROS COMPLEXOS
Nem todos os números são reais. O conjunto C dos números da forma a bi, onde a e b são reais e i2 1, é
chamado de conjunto dos números complexos. Como todo número real x pode ser representado na forma x 0i,
segue que todo número real também é complexo.
Exemplo 1.6
são exemplos de números complexos não reais.
ORDEM DE OPERAÇÕES
Em expressões envolvendo combinações de operações, a seguinte ordem é observada:
1. Primeiramente, execute operações entre símbolos agrupados. Se os símbolos agrupados estão dentro de outro
agrupamento de símbolos, proceda a partir dos agrupamentos mais internos para os mais externos.
2. Calcule expoentes antes de multiplicações e divisões, a não ser que o agrupamento de símbolos indique o contrário.
3. Calcule multiplicações e divisões, da esquerda para a direita, antes de calcular adições e subtrações (também
da esquerda para direita), a não ser que os símbolos de operações indiquem o contrário.
Exemplo 1.7
Calcule (a)
(b)
(c)
(a)
(b)
(c)
Problemas Resolvidos
1.1 Demonstre a lei distributiva estendida a(b c d) ab ac ad.
1.2 Prove que a multiplicação é distributiva em relação à subtração: a(b c) ab ac.
1.3 Mostre que (a b) a b.
Livro_Safier.indb 4
14/06/11 16:59
5
CAPÍTULO 1 • PRELIMINARES
1.4 Mostre que se
Considere
então
. Pela definição de divisão,
significa que ab1 cd1. Logo,
1.5 Prove que se a b, então a c b c.
Considere que a b. Logo b a é positivo. Mas b a b a 0 b a c (c), de acordo com as leis de
identidade e inverso. Como b a c (c) b a c c b c (a c) pela definição de subtração, pelas
leis associativa e comutativa e pelo Problema 1.3, segue que b c (a c) é positivo. Logo a c b c.
1.6 Identifique como membros dos conjuntos N, Z, Q, H, R ou C:
(a) 7
(b) 0,7
(d)
(e)
(c)
(a) 7 é um inteiro negativo; portanto é também racional, real e complexo. 7 é elemento de Z, Q, R e C.
(b) 0,7 7/10; logo é um número racional e, por isso, é real e complexo. 0,7 pertence a Q, R e C.
(c)
(d)
(e)
é um número irracional; desse modo, é também real e complexo.
é elemento de H, R e C.
não é definido. Não é elemento de qualquer um desses conjuntos.
não é número real, mas pode ser escrito como i
; portanto, é um número complexo.
está em C.
1.7 Verifique se é verdadeiro ou falso:
(a) 7 8
(b) 22/7
(c) x2 0 para todo real x.
(a) Como (8) (7) 1 é negativo, 8 7; portanto, a sentença é falsa.
(b) Uma vez que é um número irracional* e 22/7 é racional, a afirmação é falsa.
(c) Isso segue da propriedade 2 para desigualdades; a sentença é verdadeira.
1.8 Reescreva o que se segue sem usar o símbolo para valor absoluto e simplifique:
(a) 3 5
(b) 3 5
(d) x 5 se x 5
(e) x 6 se x 6
(a) 3 5 2 2
(b) 3 5 3 5 2
(c) 2 (c) Como 2 , 2 é negativo. Por isso, 2 (2 ) 2.
(d) Dado que x 5, x 5 é positivo. Logo, x 5 x 5.
(e) Dado que x 6, x (6) x 6 é negativo. Desse modo, x 6 (x 6) x 6.
* N. de T.: Existem demonstrações bem conhecidas para a irracionalidade de , mas este é um conteúdo que foge do escopo
deste livro.
Livro_Safier.indb 5
14/06/11 16:59
6
PRÉ-CÁLCULO
Problemas Complementares
1.9 Identifique a lei que justifica cada uma das seguintes sentenças:
(a) (2x 3) 5 2x (3 5)
(b) 2x (5 3x) 2x (3x 5)
(c) x (x y) x x x y
(d) 100[0,01(50 x) ] [100(0,01)](50 x)
(e) Se a b 0, então b a.
(f) Se (x 5)(x 3) 0, então x 5 0 ou x 3 0.
2
2
2
Resp. (a) Lei associativa para adição (b) Lei comutativa para adição
(c) Lei distributiva
(d) Lei associativa para multiplicação.
(e) Lei de inverso para adição
(f) Lei de fator zero
1.10 As seguintes sentenças são verdadeiras ou falsas?
(a) 3 é um número real.
(b) 3,14
(c) x 5 x 5
(d) Todo número racional é também um número complexo.
Resp. (a) verdadeira;
(b) falsa;
(c) falsa;
(d) verdadeira
1.11 Insira a desiguadade adequada entre os números que se seguem:
(a) 9 ? 8
(d)
(b) ? 4
?
(c)
? 0,33
Resp. (a) ;
(e) 1,414 ? (b) ;
(c) ;
(d) ;
(e) . (Sugestão: Assuma, por hipótese, que ad bc; em seguida comece com ab1 e
1.12 Mostre que se ad bc, então
transforme essa expressão em cd 1, por analogia ao Problema 1.4.)
1.13 Prove que
se, e somente se, ad bc.
é consequência da lei que diz que
1.14 Reescreva o que se segue sem usar o símbolo de valor absoluto e, então, simplifique:
(a) (5) [(9)]
(b) (c) 6 x, se x 6
(d) 4 x2
Resp. (a) 14;
(b) 1,4 1.15 Calcule (a)
Resp. (a) 94;
(c) x 6;
;
1,4
(d) 4 x2
(b)
(b) 23;
(c)
(c) 1936
1.16 Considere o conjunto
(a) Quais elementos desse conjunto pertencem a N?
(b) Quais elementos desse conjunto pertencem a Z?
(c) Quais elementos desse conjunto pertencem a Q?
(d) Quais elementos desse conjunto pertencem a H?
Resp. (a)
(b)
(c)
(d)
1.17 Um conjunto é fechado em relação a uma operação se o resultado da aplicação dela para quaisquer elementos do conjunto também pertence ao conjunto. Logo, os inteiros Z são fechados em relação a , enquanto os números irracionais
H não são, uma vez que, por exemplo, () 0 , que não é irracional. Identifique como verdadeiro ou falso:
(a) Z é fechado em relação a multiplicação.
(b) H é fechado em relação a multiplicação.
(c) N é fechado em relação a subtração.
(d) Q é fechado em relação a adição.
(e) Q é fechado em relação a multiplicação.
Resp. (a) verdadeiro;
Livro_Safier.indb 6
(b) falso;
(c) falso;
(d) verdadeiro;
(e) verdadeiro
14/06/11 16:59