Eletrodinâmica 2 - Lógico Cursos Aliados

1. Numa instalação elétrica de um escritório, são colocadas 3 lâmpadas idênticas em paralelo
conectadas a uma fonte de tensão.
Se uma das lâmpadas queimar, o que acontecerá com a corrente nas outras lâmpadas?
a) Aumentará por um fator 1,5.
b) Aumentará por um fator 2.
c) Diminuirá por um fator 1,5.
d) Diminuirá por um fator 2.
e) Permanecerá a mesma.
2.
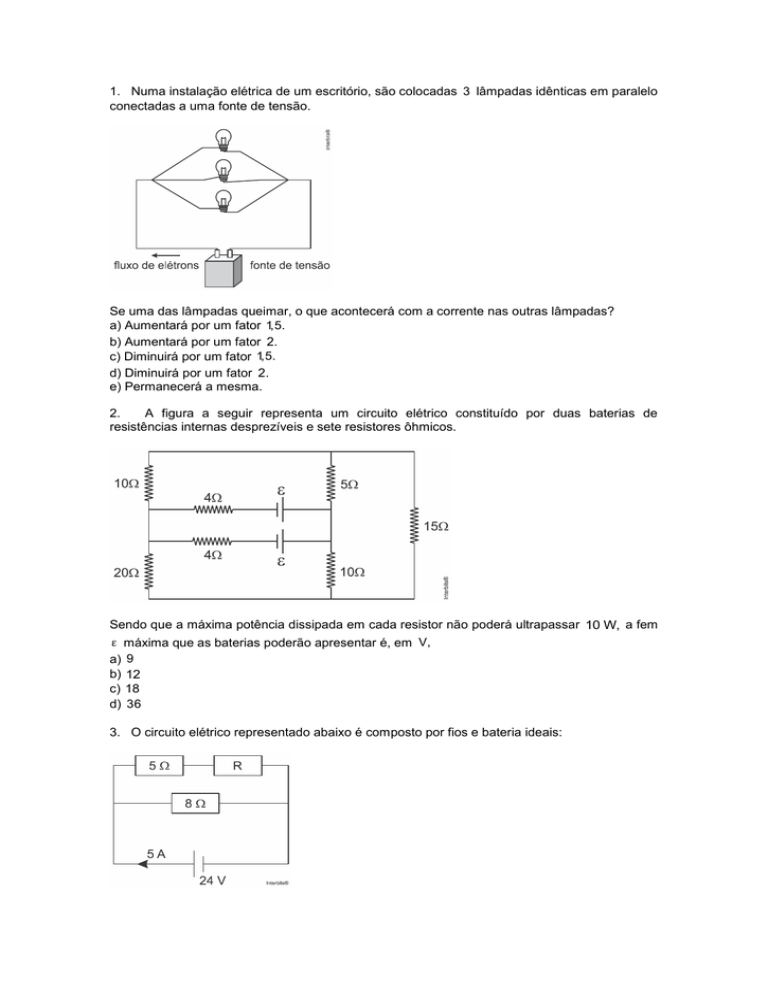
A figura a seguir representa um circuito elétrico constituído por duas baterias de
resistências internas desprezíveis e sete resistores ôhmicos.
Sendo que a máxima potência dissipada em cada resistor não poderá ultrapassar 10 W, a fem
ε máxima que as baterias poderão apresentar é, em V,
a) 9
b) 12
c) 18
d) 36
3. O circuito elétrico representado abaixo é composto por fios e bateria ideais:
Com base nas informações, qual o valor da resistência R indicada?
a) 5Ω.
b) 6Ω.
c) 7Ω.
d) 8Ω.
e) 9Ω.
4. O mostrador digital de um amperímetro fornece indicação de 0,40 A em um circuito elétrico
simples contendo uma fonte de força eletromotriz ideal e um resistor ôhmico de resistência
elétrica 10 Ω.
Se for colocado no circuito um outro resistor, de mesmas características, em série com o
primeiro, a nova potência elétrica dissipada no circuito será, em watts:
a) 0,64.
b) 0,32.
c) 0,50.
d) 0,20.
e) 0,80.
5. Dispondo de algumas pilhas idênticas, de resistência interna desprezível, fios e pequenas
lâmpadas de mesma potência, um estudante monta alguns tipos diferentes de circuitos
elétricos, conforme a figura a seguir.
Em relação aos fios ideais, considere as afirmativas sobre a corrente que circula pelos
circuitos.
I. A corrente circula pelo circuito 2 é menor que a do circuito 4.
II. A corrente que circula pelo circuito 1 é menor que a do circuito 3.
III. A corrente que circula pelo circuito 1 é menor que a do circuito 4.
IV. No circuito 2, quando a corrente passa pelo ponto A, ela é maior do que quando passa
pelo B.
Assinale a alternativa que apresenta apenas afirmativas corretas.
a) I e II.
b) II e III.
c) I e IV.
d) III e IV.
6. Três lâmpadas idênticas foram ligadas no circuito esquematizado. A bateria apresenta
resistência interna desprezível, e os fios possuem resistência nula. Um técnico fez uma análise
do circuito para prever a corrente elétrica nos pontos: A, B, C, D e E; e rotulou essas correntes
de IA , IB, IC, ID e IE , respectivamente.
O técnico concluiu que as correntes que apresentam o mesmo valor são:
a) IA  IE e IC  ID.
b) IA  IB  IE e IC  ID.
c) IA  IB, apenas.
d) IA  IB  IE, apenas.
e) IC  IB, apenas.
7.
Uma lâmpada pequena possui as seguintes especificações: 10 V e 12 W. Com essa
lâmpada e uma pilha com força eletromotriz de 12 V, pode-se montar um circuito elétrico
simples para representar o seu funcionamento.
Com os elementos citados acima, qual dos circuitos elétricos a seguir representa o circuito
simples corretamente?
a)
b)
c)
d)
e)
8. O arranjo experimental representado na figura é formado por uma fonte de tensão F, um
amperímetro A, um voltímetro V, três resistores, R1, R2 e R3, de resistências iguais, e fios de
ligação.
Quando o amperímetro mede uma corrente de 2 A, e o voltímetro, uma tensão de 6 V, a
potência dissipada em R2 é igual a:
Note e adote:
- A resistência interna do voltímetro é muito maior que a dos resistores (voltímetro ideal).
- As resistências dos fios de ligação devem ser ignoradas.
a) 4 W
b) 6 W
c) 12 W
d) 18 W
e) 24 W
9.
De um trecho de um circuito mais complexo, em que as setas indicam o sentido
convencional da corrente elétrica, são conhecidas as informações apresentadas na figura
abaixo. Quanto aos valores que podem ser calculados no circuito, identifique as afirmativas a
seguir como verdadeiras (V) ou falsas (F):
(
) A resistência elétrica no resistor R5 é de 3 .
(
) A tensão elétrica no resistor R1 é de 2 V.
) A potência dissipada pelo resistor R 4 é de 9 W.
( ) O valor da resistência elétrica R6 é de 6 .
Assinale a alternativa que apresenta a sequência correta, de cima para baixo.
a) V – F – V – F.
b) V – V – F – V.
c) F – F – V – V.
d) F – V – F – F.
e) V – F – V – V.
(
10. Tendo em vista a grande dificuldade em armazenar energia elétrica, a invenção da pilha
representou um marco histórico importante.
Para demonstrar a versatilidade da pilha em circuitos elétricos fechados, um professor elaborou
uma experiência usando uma pilha, duas chaves, duas lâmpadas e alguns pedaços de fio,
construindo um circuito elétrico capaz de atender, em momentos distintos, as seguintes
funções:
I. acender as duas lâmpadas ao mesmo tempo;
II. acender apenas uma lâmpada e manter, ao mesmo tempo, a outra apagada, podendo esta
ação ser feita para ambas as lâmpadas;
III. manter apagadas as duas lâmpadas.
Sabendo que as tensões e correntes obtidas no circuito construído eram suficientes para que
as lâmpadas se acendessem sem se queimarem, assinale a alternativa que contenha o
esquema que corresponde ao circuito construído pelo professor.
a)
b)
c)
d)
e)
11. Muitos dispositivos de aquecimento usados em nosso cotidiano usam resistores elétricos
como fonte de calor. Um exemplo é o chuveiro elétrico, em que é possível escolher entre
diferentes opções de potência usadas no aquecimento da água, por exemplo, morno (M),
quente (Q) e muito quente (MQ). Considere um chuveiro que usa a associação de três
resistores, iguais entre si, para oferecer essas três opções de temperatura. A escolha é feita
por uma chave que liga a rede elétrica entre o ponto indicado pela letra N e um outro ponto
indicado por M, Q ou MQ, de acordo com a opção de temperatura desejada. O esquema que
representa corretamente o circuito equivalente do chuveiro é:
a)
b)
c)
d)
12. O circuito elétrico representado no diagrama abaixo contém um gerador ideal de 21 Volts
com resistência interna desprezível alimentando cinco resistores.
Qual o valor da medida da intensidade da corrente elétrica, expressa em amperes, que
percorre o amperímetro A conectado ao circuito elétrico representado?
a) 0,5 A
b) 1,0 A
c) 1,5 A
d) 2,0 A
e) 2,5 A
Dois resistores, R1  2Ω e R2  3Ω, são associados em série e ligados a um gerador
ideal. Percebe-se que, nesta configuração, a corrente elétrica no circuito é igual a 12 A.
13.
A força eletromotriz (ε ) do gerador ideal e a diferença de potencial ( ) nos extremos de cada
resistor são, respectivamente, iguais a:
a) ε  60 V; 1  60 V; 2  60 V
b) ε  60 V; 1  24 V; 2  36 V
c) ε  14,4 V;
d) ε  14,4 V;
 24 V;
1  5,76 V;
1
2
 36 V
2  8,64 V
14. Por apresentar significativa resistividade elétrica, o grafite pode ser utilizado para simular
resistores elétricos em circuitos desenhados no papel, com o uso de lápis e lapiseiras.
Dependendo da espessura e do comprimento das linhas desenhadas, é possível determinar a
resistência elétrica de cada traçado produzido. No esquema foram utilizados três tipos de lápis
diferentes (2H, HB e 6B) para efetuar três traçados distintos.
Munida dessas informações, um estudante pegou uma folha de papel e fez o desenho de um
sorvete de casquinha utilizando-se desses traçados. Os valores encontrados nesse
experimento, para as resistências elétricas (R), medidas com o auxílio de um ohmímetro ligado
nas extremidades das resistências, são mostrados na figura. Verificou-se que os resistores
obedeciam a Lei de Ohm.
Na sequência, conectou o ohmímetro nos terminais A e B do desenho e, em seguida,
conectou-o nos terminais B e C, anotando as leituras RAB e RBC , respectivamente. Ao
R
estabelecer a razão AB qual resultado o estudante obteve?
RBC
a) 1
4
b)
7
10
c)
27
14
81
4
e)
81
d)
Duas lâmpadas, L1 (40 W  110 V) e L2 (100 W  110 V), são ligadas em paralelo, e a
associação é ligada numa fonte de 110 V.
15.
Nessa situação, em L1, a corrente elétrica é __________; a diferença de potencial é
__________, e a potência dissipada é __________ que em L2 .
As lacunas são corretamente preenchidas, respectivamente, por:
a) menor; igual; maior.
b) igual; menor; igual.
c) maior; igual; maior.
d) igual; maior; menor.
e) menor; igual; menor.
Na figura abaixo, são apresentados três circuitos com resistores de 1,0 Ω cada e bateria
de 3,0 V. Com base nos seus conhecimentos sobre associação de resistores, assinale a
proposição CORRETA.
16.
a) O resistor equivalente do circuito I é 1,5 Ω, no circuito II é 3,0 Ω e no circuito III é 0,33 Ω.
b) O circuito I apresenta uma associação mista, enquanto o circuito II apresenta uma
associação em série e o circuito III apresenta uma associação em paralelo.
c) O circuito I apresenta uma associação em série, enquanto o circuito II apresenta uma
associação em paralelo e o circuito III apresenta uma associação mista.
d) Os três circuitos, por possuírem os mesmos resistores e a mesma d.d.p., dissipam a mesma
potência.
e) O circuito I apresenta uma associação mista, enquanto o circuito II apresenta uma
associação em paralelo e o circuito III apresenta uma associação em série.
17. A resistência R na associação de resistores a seguir é igual a:
a) 10 Ω.
b) 20 Ω.
c) 30 Ω.
d) 40 Ω.
18. No circuito esquematizado abaixo R1 e R2 são resistores com a mesma resistividade p.
R1 tem comprimento 2L e seção transversal A, e R2 tem comprimento L e seção transversal
2A.
Nessa situação, a corrente elétrica que percorre o circuito é:
a) 2AV / (5pL).
b) 2AV / (3pL).
c) AV / (pL).
d) 3AV / (2pL).
e) 5AV / (2pL).
19.
A ponte de fio mostrada é constituída por uma bateria, um galvanômetro G, dois
resistores, um de resistência elétrica R1  10,0Ω e outro de resistência elétrica R2  40,0 Ω,
um fio condutor homogêneo de resistividade r, área de secção transversal A e comprimento
L  100,0 cm e um cursor C que desliza sobre o fio condutor. Quando o cursor é colocado de
modo a dividir o fio condutor em dois trechos de comprimentos L1 e L2 a corrente elétrica no
galvanômetro é nula.
Os comprimentos L1 e L2 valem, respectivamente:
a) 50,0 cm e 50,0 cm
b) 60,0 cm e 40,0 cm
c) 40,0 cm e 60,0 cm
d) 80,0 cm e 20,0 cm
e) 20,0 cm e 80,0 cm
20. É comum um componente eletrônico apresentar a especificação 2W  4V e funcionar
corretamente mesmo alimentado por uma bateria ideal de fem 12V. Nessas circunstâncias,
esse componente é associado a outro, geralmente um resistor, o que faz com que a
associação funcione normalmente. Tal resistor deve ser associado em _______ com o
componente, ter uma resistência elétrica de _______ Ω e dissipar uma potência de
_______ W.
Assinale a alternativa que preenche, correta e respectivamente, as lacunas.
a) série … 16 ... 4
b) série … 16 ... 2
c) série … 8 ... 2
d) paralelo … 16 ... 4
e) paralelo … 16 ... 2
21. Um estudante, precisando instalar um computador, um monitor e uma lâmpada em seu
quarto, verificou que precisaria fazer a instalação de duas tomadas e um interruptor na rede
elétrica. Decidiu esboçar com antecedência o esquema elétrico.
“O circuito deve ser tal que as tomadas e a lâmpada devem estar submetidas à tensão nominal
da rede elétrica e a lâmpada deve poder ser ligada ou desligada por um interruptor sem afetar
os outros dispositivos” — pensou.
Símbolos adotados:
Qual dos circuitos esboçados atende às exigências?
a)
b)
c)
d)
e)
22. Em um circuito elétrico, representado no desenho abaixo, o valor da força eletromotriz
(fem) do gerador ideal é E  1,5 V, e os valores das resistências dos resistores ôhmicos são
R1  R4  0,3 Ω, R2  R3  0,6 Ω e R5  0,15 Ω. As leituras no voltímetro
amperímetro A, ambos ideais, são, respectivamente:
V
e no
a) 0,375 V e 2,50 A
b) 0,750 V e 1,00 A
c) 0,375 V e 1,25 A
d) 0,750 V e 1,25 A
e) 0,750 V e 2,50 A
23. Em uma aula no laboratório de Física, o professor solicita aos alunos que meçam o valor
da resistência elétrica de um resistor utilizando um voltímetro ideal e um amperímetro ideal.
Dos esquemas abaixo, que representam arranjos experimentais, qual o mais indicado para a
realização dessa medição?
a) Esquema A
b) Esquema B
c) Esquema C
d) Esquema D
e) Esquema E
24. Qual desses circuitos elétricos consome a menor energia, sabendo que entre os pontos a
e b de cada circuito é aplicada a mesma tensão e que todas as resistências são iguais?
a)
b)
c)
d)
e)
25. Considere o circuito formado por três lâmpadas idênticas ligadas em paralelo à bateria,
conforme representa a figura (1).
Como a chave C foi aberta na figura (2), considere as afirmações abaixo sobre a figura (2), em
comparação à situação descrita na figura (1).
I. A potência fornecida pela bateria é a mesma.
II. A diferença de potencial aplicada a cada lâmpada acesa é a mesma.
III. As correntes elétricas que percorrem as lâmpadas acesas são menores.
Quais estão corretas?
a) Apenas II.
b) Apenas III.
c) Apenas I e II.
d) Apenas I e III.
e) I, II e III.
26. Considere o texto e a figura para analisar as afirmativas apresentadas na sequência.
No circuito elétrico mostrado na figura a seguir, um resistor de 4,0Ω e uma lâmpada, cuja
resistência elétrica é 8,0 Ω, estão ligados a uma fonte de 24V. Nesse circuito são conectados
dispositivos de medida de corrente elétrica, os amperímetros A1 e A2, e de diferença de
potencial elétrico, o voltímetro V. Assume-se que os amperímetros e o voltímetro podem ser
considerados ideais, ou seja, que seu efeito no circuito pode ser desprezado na forma como
estão ligados.
A partir da análise do circuito, afirma-se que:
I. As leituras dos amperímetros A1 e A2 são, respectivamente, 2,0A e 2,0A.
II. A leitura do voltímetro V é 24V.
III. As potências dissipadas no resistor e na lâmpada são, respectivamente, 16W e 32W.
Está(ão) correta(s) a(s) afirmativa(s):
a) I, apenas.
b) I e II, apenas.
c) I e III, apenas.
d) II e III, apenas.
e) I, II e III.
27. Fusíveis são dispositivos de proteção de um circuito elétrico, sensíveis ao excesso de
corrente elétrica. Os modelos mais simples consistem de um filamento metálico de baixo ponto
de fusão, que se funde quando a corrente ultrapassa determinado valor, evitando que as
demais partes do circuito sejam danificadas. A figura mostra um diagrama de um circuito em
que o fusível F protege um resistor R de 12Ω, uma lâmpada L de 6 W e um alto-falante que
conduz 1A.
Sabendo que esse fusível foi projetado para trabalhar com uma corrente até 20% maior que a
corrente nominal que atravessa esse circuito, qual é o valor, em ampères, da corrente máxima
que o fusível F permite passar?
a) 1,0
b) 1,5
c) 2,0
d) 2,5
e) 3,0
28. O circuito elétrico de um certo dispositivo é formado por duas pilhas ideais idênticas, de
tensão “V” cada uma, três lâmpadas incandescentes ôhmicas e idênticas L 1, L2 e L3, uma
chave e fios condutores de resistências desprezíveis. Inicialmente, a chave está aberta,
conforme o desenho abaixo.
Em seguida, a chave do circuito é fechada. Considerando que as lâmpadas não se queimam,
pode-se afirmar que:
a) a corrente de duas lâmpadas aumenta.
b) a corrente de L1 diminui e a de L3 aumenta.
c) a corrente de L3 diminui e a de L2 permanece a mesma.
d) a corrente de L1 diminui e a corrente de L2 aumenta.
e) a corrente de L1 permanece a mesma e a de L2 diminui.
29. Em uma situação cotidiana, uma pessoa liga duas lâmpadas incandescentes em paralelo
em uma rede de 220V. As lâmpadas apresentam certa intensidade luminosa (brilho), sendo
que a lâmpada 2 tem um filamento de mesmo material, mesmo comprimento, mas é mais
grosso que o filamento da lâmpada 1.
Nessas condições, a alternativa correta é:
a) Desligando a lâmpada L1, a lâmpada L2 diminui o seu brilho.
b) A lâmpada L1 brilha mais que a lâmpada L2.
c) As lâmpadas L1 e L2 tem o mesmo brilho.
d) A lâmpada L2 brilha mais que a lâmpada L1.
30. Cinco resistores de mesma resistência R estão conectados à bateria ideal E de um
automóvel, conforme mostra o esquema:
Inicialmente, a bateria fornece ao circuito uma potência PI. Ao estabelecer um curto-circuito
entre os pontos M e N, a potência fornecida é igual a PF.
P
A razão F é dada por:
PI
a)
7
9
14
15
c) 1
7
d)
6
b)
31. Para compor a decoração de um ambiente, duas lâmpadas idênticas, L 1 e L2, com valores
nominais (100 V – 100 W), devem ser ligadas em paralelo a uma fonte de tensão constante de
200 V. Deseja-se que L1 brilhe com uma potência de 100 W e que L2 brilhe com uma potência
de 64 W. Para que as lâmpadas não queimem, dois resistores ôhmicos, R 1 e R2, com valores
convenientes, são ligados em série com as respectivas lâmpadas, conforme o esquema
representado na figura.
Considerando todos os fios utilizados na ligação como ideais e que as lâmpadas estejam
acesas e brilhando com as potências desejadas, é correto afirmar que os valores das
resistências de R1 e R2, em ohms, são, respectivamente, iguais a:
a) 200 e 100.
b) 200 e 150.
c) 100 e 150.
d) 100 e 300.
e) 100 e 200.
32. Considere que um determinado estudante, utilizando resistores disponíveis no laboratório
de sua escola, montou os circuitos apresentados abaixo:
Querendo fazer algumas medidas elétricas, usou um voltímetro (V) para medir a tensão e um
amperímetro (A) para medir a intensidade da corrente elétrica. Considerando todos os
elementos envolvidos como sendo ideais, os valores medidos pelo voltímetro (situação 1) e
pelo amperímetro (situação 2) foram, respectivamente:
a) 2V e 1,2A
b) 4V e 1,2A
c) 2V e 2,4A
d) 4V e 2,4A
e) 6V e 1,2A
33. O circuito elétrico seguinte é constituído por três lâmpadas L1 , L2 e L3, que são idênticas,
e ligadas a uma bateria ε.
Se a lâmpada L3 repentinamente se queimar, é correto afirmar que:
a) L2 diminuirá o seu brilho.
b) L1 dissipará mais energia.
c) L2 dissipará menos energia.
d) L1 terá o mesmo brilho de L2.
34.
Considere um circuito formado por dois resistores ôhmicos, R1 e R2, em série com uma
bateria. Neste circuito, a energia dissipada por unidade de tempo pelo resistor R2 é o dobro do
que a dissipada pelo resistor R1. Sendo I1 e I2 as correntes elétricas que circulam pelos
resistores, e V1 e V2 as quedas de potencial nos respectivos resistores, é correto afirmar que:
a) V1  V2;
b) V1  V2;
I 1 I 2;
I 1 I 2;
c) V1  V2; I 1 I 2;
d) V1  V2; I 1 I 2;
e) V1  V2; I 1 I 2;
R1  R2.
R1  R2.
R1  R2.
2R1  R2.
R1  2R2.
35.
Um sistema de iluminação foi construído com um circuito de três lâmpadas iguais
conectadas a um gerador (G) de tensão constante. Esse gerador possui uma chave que pode
ser ligada nas posições A ou B.
Considerando o funcionamento do circuito dado, a lâmpada 1 brilhará mais quando a chave
estiver na posição:
a) B, pois a corrente será maior nesse caso.
b) B, pois a potência total será maior nesse caso.
c) A, pois a resistência equivalente será menor nesse caso.
d) B, pois o gerador fornecerá uma maior tensão nesse caso.
e) A, pois a potência dissipada pelo gerador será menor nesse caso.
36.
Um cabo subterrâneo inicialmente isolado, instalado entre os pontos A e B, possui
resistência de 0,01 /m. Este cabo se rompeu e seu ponto de ruptura apresenta fuga de
corrente para a terra. Para determinar o ponto de rompimento do cabo e escavar o terreno de
modo a sanar o problema, foi montado o aparato apresentado na figura acima, composto por
uma bateria Vb ajustada para fornecer uma corrente constante de 10 A ao circuito formado
pela resistência R e pelo cabo. O valor da tensão da bateria é mostrado por um voltímetro que
apresenta um erro de medição de +/–10%. Sabendo que a leitura do voltímetro é 16,67 V, é
CORRETO afirmar que:
a) a partir da leitura do voltímetro no ensaio, pode-se concluir que o comprimento total do cabo
é 2 km.
b) a distância mínima de x para se iniciar a escavação é 224 m.
c) a distância máxima de x para se encerrar a escavação é 176 m.
d) o ponto x = 240 m está dentro do intervalo provável de ruptura do cabo.
e) o ponto x = 210 m está dentro do intervalo provável de ruptura do cabo.
37.
No circuito elétrico esquematizado abaixo, a leitura no amperímetro A não se altera
quando as chaves C1 e C2 são simultaneamente fechadas.
Considerando que a fonte de tensão ε, o amperímetro e os fios de ligação são ideais e os
resistores ôhmicos, o valor de R é igual a:
a) 50 .
b) 100 .
c) 150 .
d) 600 .
38. Os manuais dos fornos micro-ondas desaconselham, sob pena de perda da garantia, que
eles sejam ligados em paralelo juntamente a outros aparelhos eletrodomésticos por meio de
tomadas múltiplas, popularmente conhecidas como “benjamins” ou “tês”, devido ao alto risco
de incêndio e derretimento dessas tomadas, bem como daquelas dos próprios aparelhos.
Os riscos citados são decorrentes da:
a) resistividade da conexão, que diminui devido à variação de temperatura do circuito.
b) corrente elétrica superior ao máximo que a tomada múltipla pode suportar.
c) resistência elétrica elevada na conexão simultânea de aparelhos eletrodomésticos.
d) tensão insuficiente para manter todos os aparelhos eletrodomésticos em funcionamento.
e) intensidade do campo elétrico elevada, que causa o rompimento da rigidez dielétrica da
tomada múltipla.
39. Um circuito em série é formado por uma pilha, uma lâmpada incandescente e uma chave
interruptora. Ao se ligar a chave, a lâmpada acende quase instantaneamente, irradiando calor e
luz. Popularmente, associa-se o fenômeno da irradiação de energia a um desgaste da corrente
elétrica, ao atravessar o filamento da lâmpada, e à rapidez com que a lâmpada começa a
brilhar. Essa explicação está em desacordo com o modelo clássico de corrente.
De acordo com o modelo mencionado, o fato de a lâmpada acender quase instantaneamente
está relacionado à rapidez com que:
a) o fluido elétrico se desloca no circuito.
b) as cargas negativas móveis atravessam o circuito.
c) a bateria libera cargas móveis para o filamento da lâmpada.
d) o campo elétrico se estabelece em todos os pontos do circuito.
e) as cargas positivas e negativas se chocam no filamento da lâmpada.
40. No circuito da figura abaixo, a diferença de potencial, em módulo, entre os pontos A e B é
de:
a) 5 V.
b) 4 V.
c) 3 V.
d) 1 V.
e) 0 V.
41. Um eletricista analisa o diagrama de uma instalação elétrica residencial para planejar
medições de tensão e corrente em uma cozinha. Nesse ambiente existem uma geladeira (G),
uma tomada (T) e uma lâmpada (L), conforme a figura. O eletricista deseja medir a tensão
elétrica aplicada à geladeira, a corrente total e a corrente na lâmpada. Para isso, ele dispõe de
um voltímetro (V) e dois amperímetros (A).
Para realizar essas medidas, o esquema da ligação desses instrumentos está representado
em:
a)
b)
c)
d)
e)
42. Um grupo de amigos foi passar o fim de semana em um acampamento rural, onde não há
eletricidade. Uma pessoa levou um gerador a diesel e outra levou duas lâmpadas, diferentes
fios e bocais. Perto do anoitecer, iniciaram a instalação e verificaram que as lâmpadas eram de
60 W – 110 V e o gerador produzia uma tensão de 220 V.
Para que as duas lâmpadas possam funcionar de acordo com suas especificações e o circuito
tenha menor perda possível, a estrutura do circuito elétrico deverá ser de dois bocais ligados
em:
a) série e usar fios de maior espessura.
b) série e usar fios de máximo comprimento.
c) paralelo e usar fios de menor espessura.
d) paralelo e usar fios de maior espessura.
e) paralelo e usar fios de máximo comprimento.
43. Considere o circuito a seguir.
No circuito, por onde passa uma corrente elétrica de 4 A, três resistores estão conectados a
uma fonte ideal de força eletromotriz de 20 V.
Os valores da resistência total deste circuito e da resistência RX são, respectivamente:
a) 0,8  e 2,6 .
b)
c)
d)
e)
0,8  e 4,0 .
5,0  e 5,0 .
5,0  e 10,0 .
10,0  e 4,0 .
44. No manual de uma máquina de lavar, o usuário vê o símbolo:
Este símbolo orienta o consumidor sobre a necessidade de a máquina ser ligada a:
a) um fio terra para evitar sobrecarga elétrica.
b) um fio neutro para evitar sobrecarga elétrica.
c) um fio terra para aproveitar as cargas elétricas do solo.
d) uma rede de coleta de água da chuva.
e) uma rede de coleta de esgoto doméstico.
Gabarito:
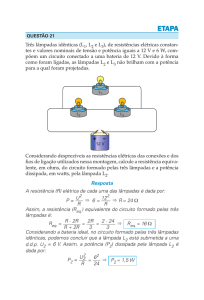
Resposta
[E]
da
questão
1:
A quantidade de corrente que passa em cada lâmpada permanecerá a mesma, pois em um
circuito em paralelo, com todas as lâmpadas possuindo a mesma resistência, a quantidade de
corrente em cada lâmpada sempre será a mesma.
O que acontecerá é que o gerador vai precisar enviar menos corrente elétrica e,
consequentemente, o dono do escritório irá pagar uma conta de luz menor (caso ele não troque
a lâmpada).
Resposta
[C]
da
questão
2:
Nomeando os nós e os resistores:
Redesenhando e fazendo as simplificações convenientes.
Analisando essa nova configuração, vê-se que há uma ponte de Wheatstone em equilíbrio
entre os nós A e E, pois:
R1  R4  R2  R3  100 Ω.
Assim, o resistor R5 pode ser eliminado, pois não passa corrente por ele. A figura a seguir
mostra uma nova simplificação e as intensidades relativas das correntes.
As potências dissipadas são:
P  5  2i 2  20i2
 1
P  10i2
 2

2
P3  10  2i   40i2

P4  20i2
Nota-se, então, que o resistor que dissipa maior potência é R3. Assim:
P3  10  40i2  10  i2 
1
 i  0,5 A.
4
A corrente total no circuito é:
I  3i  3 0,5   I  1,5 A.
Aplicando a Lei de Ohm-Pouillet:
15  30

ε  Req I  ε  
 2  1,5 
 15  30

Resposta
[C]
ε  18 V.
da
questão
3:
Usando a primeira Lei de Ohm, obtemos a resistência equivalente do circuito:
U
24 V
U  Req  i  Req   Req 
 Req  4,8 Ω
i
5A
Observando o circuito temos em série os resistores R e de 5 Ω e em paralelo com o resistor
de 8 Ω.
Assim,
1
1
1
1
1
1






Req 8 Ω R  5 Ω
4,8 Ω 8 Ω R  5 Ω

8 Ω  4,8 Ω
1
3,2 Ω
1




2
4,8 Ω  8 Ω R  5 Ω
R

5Ω
38,4 Ω
 R  5 Ω  12 Ω  R  7 Ω
Resposta
[E]
da
Para o circuito inicialmente proposto, temos que:
questão
4:
U  R i
U  10  0,4
U4V
Inserindo outro resistor no circuito, de mesmas características que o primeiro, em série,
teremos que a resistência total do circuito passará a ser de 20 Ω. Assim,
U  R e q  i'
4
20
i'  0,2 A
i' 
Desta forma, a potência total dissipada pelo circuito será de:
P  i U
P  0,2  4
P  0,8 W
Resposta
[A]
da
questão
Quando um circuito está em série, as resistências são somadas (Req  R1  R2 
quando a d.d.p. está em série, ela é somada (Ueq  U1  U2 
5:
 Rn ),
 Un ), e quando a d.d.p. está
em paralelo, nada muda (se você pensar em duas pilhas em paralelo, o que acontecerá que o
circuito funcionará por mais tempo, com a mesma d.d.p).
U
R
U

2R
2U

R
U

R
i1 
i2
i3
i4
Resposta
[A]
i3  i1  i4  i2
da
questão
6:
As três lâmpadas estão em paralelo. Como são idênticas, são percorridas pela mesma
corrente, i.
A figura mostra a intensidade da corrente elétrica em cada lâmpada e nos pontos destacados.
De acordo com a figura:
IA  3i; IB  2i; IC  i; ID  i e IE  3i.
Portanto:
IA  IE e IC  ID .
Resposta
[A]
da
questão
7:
O enunciado diz que a lâmpada possui 10 V e 12 W, e é aplicado uma força eletromotriz de
12 V, para a lâmpada possuir o desempenho e a iluminação adequada é necessário uma
resistência para criar justamente uma resistência e a lâmpada não queimar, pois ela foi
fabricada para funcionar com 10 V e está sendo aplicando uma tensão de 12 V.
Resposta
[A]
da
questão
8:
O esquema mostra o circuito e as distribuições de tensão corrente.
Os dois ramos do circuito estão em paralelo. No ramo inferior a resistência é metade da do
ramo superior, logo a corrente é o dobro.
Assim:
i12  i 3  I  i  2i  2
2
A.
3
 i
i12  i 
2
A
3
i3  2i 
4
A
3
Os resistores de resistência R1 e R2 têm resistências iguais e estão ligados em série. Então
estão sujeitos à mesma tensão, U2  U1  6 V.
Assim, a potência dissipada em R2 é:
2
P2  U2 i12  6 

P2  4 W.
3
Resposta
[C]
da
[F] A resistência elétrica no resistor R5 é de 3 .

i4  i0  i3  0,2  1,3  i4  1,5 A.


Da figura: i4  i5  i6  1,5  1  i6  i6  0,5 A.

U  R i  6  R  0,5   R  6 
5
5 5
5
5

0,5

questão
9:
R5  12 Ω.
[F] A tensão elétrica no resistor R1 é de 2 V.
No resistor R2 a corrente é i2 . Aplicando a lei de Ohm:
U2  R2 i 2  2  4i 2  i2  0,5 A.
Sendo i1 a corrente em R1, pela lei dos nós:
i 1  i2  i3  i1  0,5  1,3  i1  0,8 A.
Calculando a tensão em R1 :
U1  R1 i1  3  0,8 
U1  2,4 V.
[V] A potência dissipada pelo resistor R 4 é de 9 W.
P4  R 4 i 24  4 1,5   4  2,25 
2
P4  9 W.
[V] O valor da resistência elétrica R6 é de 6 .
Os resistores R5 e R6 estão em paralelo. Logo estão sob mesma tensão:
U6  U5  6 V.


U6  R6 i6  6  R 6 1 

Resposta
[A]
R 6  6 Ω.
da
questão
10:
No circuito da alternativa [A] as duas lâmpadas estão em paralelo. Da maneira como mostrado,
as duas lâmpadas estão apagadas, pois as duas chaves estão abertas, satisfazendo a
condição III.
Fechando-se as duas chaves, acendem as duas lâmpadas, satisfazendo a condição I.
Ligando-se apenas uma das chaves, apenas uma das lâmpadas acende, satisfazendo a
condição II.
Resposta
[A]
da
questão
11:
Como a diferença de potencial (U) é a mesma nos três casos, a potência pode ser calculada
pela expressão:
P
U2
.
R
Assim, a conexão de menor resistência equivalente é a que dissipa a maior potência:
Como:
PMQ  PQ  PM  RMQ  RQ  RM.
A figura ilustra essas conexões:
Resposta
[B]
da
questão
12:
questão
13:
questão
14:
A resistência equivalente do paralelo é:
63
Rp 
 2 Ω.
63
A resistência equivalente do circuito é:
Req  2  3  1  1  7 Ω.
Aplicando a lei de Ohm-Pouillet:
E  Req I  21  7I  I  3 A.
A ddp no trecho em paralelo é:
Up  Rp I  2  3  6 V.
Então, a leitura do amperímetro é:
Up  Ri A  6  6i A 
iA  1 A.
Resposta
[B]
da
Aplicando a Lei de Ohm Pouillet:
ε  R1  R2  i  ε   2  3 12  ε  60 V.
U1  R1 i  2  12  U1  24 V.
U2  R2 i  3  12  U2  36 V.
Resposta
[B]
da
Esquematizando a 1ª situação proposta e fazendo as simplificações:
A resistência equivalente nessa situação 1 é:
1
1 1
1
4  1 1 6
3
10
 




 R AB 
.
R AB 5 20 20
20
20 10
3
Esquematizando a 2ª situação proposta e fazendo as simplificações:
No ramo superior da figura acima a resistência equivalente é:
20  5
RBC1 
 10  4  10  RBC1  14 .
25
A resistência equivalente na situação 2 é:
14  10 140
35
RBC 

 RBC 
.
24
24
6
Fazendo a razão pedida:
10
RAB
3  10  6  20 

35
RBC
3 35 35
6
Resposta
[E]
RAB 4
 .
RBC 7
da
questão
15:
Para o circuito em paralelo, as tensões são iguais para as duas lâmpadas, podendo calcular as
intensidades das correntes para cada uma:
P
P  Ui  i 
U
40 W
i1 
 0,36 A
110 V
i2 
100 W
 0,91 A
110 V
Logo, podemos afirmar que a lâmpada 1 em relação à 2 tem a potência menor, a ddp é a
mesma e a potência dissipada é menor como informa os dados de cada uma.
Resposta
da
questão
16:
[E]
- Circuito I: associação mista de resistência equivalente RI 
3R
.
2
R
.
3
- Circuito III: associação em série de resistência equivalente RIII  3R.
- Circuito II: associação em paralelo de resistência equivalente RII 
Resposta
[C]
da
questão
17:
É direto visualizar que trata-se de uma associação mista de resistores, onde
 40 Ω  / /  20 Ω  / / 10  R . Assim, utilizando os dados do enunciado, podemos encontrar a
tensão aplicada entre os pontos A e B.
UAB  U2  R2  i2
UAB  20  6
UAB  120 V
Com o valor desta tensão, podemos encontrar a corrente que circula pelo resistor de 40 ohms.
UAB  R1  i1
120  40  i1
i1  3 A
Assim, pela lei dos nós de Kirchhoff, podemos encontrar a corrente elétrica que passa pela
associação de resistores em série 10  R  .
i  i1  i2  i3
12  3  6  i3
i3  3 A
Por fim, com o valor da corrente no ramo 3, podemos encontrar o valor do resistor R pedido no
enunciado:
UAB  10  R   i3
120  10  R   3
3  R  90
R  30 Ω
Resposta
[A]
da
questão
18:
Os resistores estão associados em série, portanto a resistência equivalente é a soma das
resistências. Aplicando a segunda lei de Ohm:

ρ 2L 2 ρ L

R1 
2ρL ρ L
5ρ L
A
A

 Re q  R1  R 2 

 Re q 
.

ρ
L
A
2
A
2A
R 2 
2A


V  R eq i  i 
Resposta
[E]
V

5ρ L
2A
i
2 AV
.
5ρ L
da
questão
19:
Trata-se de uma ponte de Wheststone em equilíbrio.
L1  L2  100  L2  100  L1


R1 L2  R2 L1  10 100  L1   40 L1  L1  20 cm.

Resposta
[A]
da

L 2  80 cm.
questão
20:
Para esta questão, é necessário lembrar do conceito de divisor de tensão. Para que eu consiga
fornecer somente 4 Volts ao componente eletrônico, tendo como alimentação uma bateria de
12 Volts, é necessário que seja colocado um resistor em série com este, para que a tensão
seja dividida entre eles. Assim, temos o seguinte circuito elétrico:
Para o funcionamento correto do componente eletrônico (2W / 4V), teremos que a corrente
elétrica no circuito será de:
P  iU
2
4
i  0,5 A
i
Assim, pela 1ª Lei de Ohm, podemos encontrar o valor da resistência a ser inserida no circuito.
U
8
R 
i 0,5
R  16 Ω
E a potência dissipada por este será de:
P  R  i2  16  0,5 
2
P4W
Resposta
[E]
da
questão
21:
Para ficarem sob mesma ddp, os três dispositivos deve ser associados em paralelo. Porém, a
chave deve ligar e desligar apenas a lâmpada, devendo estar em série apenas com esta.
Resposta
[A]
da
O sentido da corrente elétrica é mostrado na figura.
questão
22:
Calculando a resistência equivalente do circuito:

0,9
R12  R1  R2  0,3  0,6  R12  0,9 Ω.
 R AB 
 0,45 Ω

R

R

R

0,6

0,3

R

0,9
Ω
.
2

3
4
34
 34
Req  R AB  R5  0,45  0,15  Req  0,6 Ω.
A leitura do amperímetro é a intensidade (I) da corrente no circuito.
E  Req I  I 
E
1,5


Req 0,6
I  2,5 A.
Como R12 = R34, as correntes i1 e i2 têm mesma intensidade.
I 2,5
i1  i2  
 i1  i2  1,25 A.
2
2
A leitura do voltímetro é a tensão entre os pontos C e D.
UVolt  UCD  R1 i1  R3 i2  0,3 1,25   0,3 1,25   0,375  0,75 
UVolt  0,375 V.
Resposta
[A]
da
questão
23:
Para efetuar as medidas solicitadas, o amperímetro deve ser ligado em série e o voltímetro em
paralelo ao elemento que se deseja medir. Com isso, a alternativa correta é [A].
Resposta
[D]
da
questão
24:
O circuito elétrico com menor consumo de energia será aquele que possui menor potência,
menor intensidade da corrente elétrica e maior resistência elétrica.
O circuito em série (alternativa [D]) nos fornece mais resistência à passagem da corrente
elétrica e, portanto, terá menor consumo de energia elétrica entre os outros circuitos que
apresentam ligações em paralelo ou mistas.
Resposta
[A]
da
questão
25:
[I] Incorreta. A potência fornecida pela bateria aumenta, pois há mais uma lâmpada "puxando"
corrente dessa bateria.
[II] Correta. As lâmpadas estão ligadas em paralelo, sendo a mesma ddp em todas.
[III] Incorreta. As correntes que percorrem as lâmpadas acesas não se alteram. Quando se liga
mais uma lâmpada, aumenta apenas a corrente total fornecida pela bateria.
Resposta
[C]
da
questão
26:
Dados: E  24 V; R  4 Ω; RL  8 Ω.
[I] Correta.
No voltímetro ideal não passa corrente. Então os amperímetros fornecem a mesma leitura (L A),
o valor da corrente elétrica i, como indicado na figura.
Aplicando a lei de Ohm-Pouillet:
i
E
24
 i
R  RL
48
i2 A 
L A  2 A.
[II] Incorreta.
A leitura do voltímetro (LV) é a ddp entre os pontos A e B.
L V  UAB  RL i  8  2

L V  16 V.
[III] Correta.
As potências dissipadas no resistor (PR) e na lâmpada (PL) são:

2
2
PR  R i  4  2   PR  16 W.

P  R i 2  8 2 2  P  32 W.
 
L
L
 L
Resposta
[E]
da
questão
27:
Os três dispositivos estão ligados em paralelo, submetidos à ddp U  12V.
Calculando a corrente total máxima (I):

U 12
 iR  1 A.
No resistor: U  R iR  iR  
R
12

PL
6


 iL  0,5 A.
 I  1,2 i R  i L  i A  
Na lâmpada: PL  U i L  iL 
U 12

No alto-falante: iA  1 A.


I  1,2 1  0,5  1 
Resposta
[A]
I  3 A.
da
questão
28:
Seja R a resistência de cada lâmpada e U a ddp fornecida pela associação das duas pilhas.
Calculemos a corrente em cada lâmpada nos dois casos, usando a 1ª lei de Ohm:
CHAVE ABERTA:
A resistência equivalente é:
Rab  R  R  2 R.
A corrente gerada é:
U
U
Iab 

.
Rab 2 R
As correntes nas lâmpadas são:
U
i1  i2  Iab 
 0,5 R; i3  0.
2R
CHAVE FECHADA:
A resistência equivalente é:
R 3 R
Rfec  R  
.
2
2
A corrente gerada é:
2U
U
U
I fec 


R fec 3 R 3 R
2
 I fec  0,67
U
.
R
As correntes nas lâmpadas são:
I
U
i1  Ifec  0,67 ; i2  i3  fec  0,33 R.
R
2
Conclusão: i1 e i3 aumentam e i2 diminui.
Resposta
[D]
da
questão
29:
Como as lâmpadas estão ligadas em paralelo, ambas estão sob mesma tensão, U = 220 V.
Para um resistor de resistência R, comprimento L, secção transversal de área A e feito de
material de resistividade ρ, a potência dissipada está relacionada a essas grandezas pela
expressão abaixo.

U2
P

U2

R
  P
A

ρL
R  ρ L


A
O brilho está relacionado à potência dissipada que, como mostra essa expressão, é
diretamente proporcional à área da secção transversal. Portanto, brilha mais a lâmpada de
filamento mais grosso, que é a lâmpada L1.
Resposta
[D]
da
questão
30:
Estabelecendo um curto-circuito, popularmente conhecido como “chupeta”, entre os pontos M e
N, os três resistores em paralelo não mais funcionam.
Para as duas situações inicial e final, as respectivas resistências equivalentes são:
R
7

RI  3  2 R  3 R.


R  2 R.
 F

Calculando as potências dissipadas:

3 E2
E2
PI 

7R
7 R

P
7 R
U2
E2

3
Pd 

  F

R
PI 2 R 3 E 2

E2
PF 
2 R


Resposta
[C]
da

PF 7
 .
PI 6
questão
31:
Na lâmpada 1:
P1  U1 i1  100  100 i1  i1  1 A.
U  U1  R1 i1  200  100  R1 1 
R1  100 Ω.
Na lâmpada 2, supondo que a resistência mantenha-se constante:

U2
P2  2

R

2
U'2

P'

 2
R
 
P'2  U'2 i2
 64  80 i2
P2
U2
R
 2 2
P'2
R U'2

100  100 


64  U'2 
2

10 100

 U'2  80 V.
8
U'2
 i2  0,8 A.
U  U'2  R2 i2  200  80  R 2  0,8   R 2 
120
0,8

R2  150 Ω.
Resposta
[B]
da
questão
32:
Situação I
Como os resistores estão em série, a resistência equivalente é igual à soma das resistências.
O valor medido pelo voltímetro é a ddp no resistor de 40.
Aplicando a lei de Ohm-Pouillet:
ε  Re q i  12   60  40  20  i  i 
U  R i  40  0,1 
12
 i  0,1 A.
120
U  4 V.
Situação II
Calculando a resistência equivalente:
1
1
1
1 1 2  3 6
1






Req 60 30 20
60
60 10
 Req  10 Ω.
O valor medido pelo amperímetro é a corrente total no circuito.
Aplicando a lei de Ohm-Pouillet:
ε
12
ε  Req i  i 

 i  1,2 A.
Req 10
Resposta
[D]
da
questão
33:
Se L3 queimar, passará a mesma corrente por L1 e L2, pois elas ficarão em série. Como elas
são idênticas, L1 terá o mesmo brilho que L2.
Resposta
[D]
da
questão
34:
Como os resistores estão associados em série, eles são percorridos pela mesma corrente:
I1  I2.
Relacionando as resistências:
2 P1  P2  2 R1 I 2  R2 I 2 
Quantos às tensões:

V1  R1 I


V2  R2 I  V2  2 R1 I
Resposta
[C]
2 R1  R2 .
 V2  2 V1 
da
V1  V2 .
questão
35:
O brilho de uma lâmpada depende da sua potência. A lâmpada de maior potência apresenta
brilho mais intenso.
Com a chave na posição A, as lâmpadas 1 e 3 ficam ligadas em paralelo e a lâmpada 2 não
R
acende; sendo R a resistência de cada lâmpada, a resistência equivalente é RA  .
2
A potência dissipada na lâmpada 1 (P1A ) é metade da potência dissipada na associação (PA ).
Se a tensão fornecida pelo gerador é U, temos:
U2 U2
2U 2

 PA 
.
RA R
R
2
P
U2
 A  P1 A 
.
2
R
PA 
P1 A
Com a chave na posição B, as lâmpadas 1 e 3 continuam em paralelo e em série com a
lâmpada 2.
A resistência equivalente (RB ), a corrente total (I), a corrente na lâmpada 1 (i1B ) e a potência
dissipada na lâmpada 1 (P1B ) são:
R
3R

RB  2  R  RB  2 .

I  U  2 U .
 3R
3R

2

i  I  U .
 1B 2 3 R


U2
U2
2
P

R
i

R

P

.
1
1B
 1B
9R
9 R2

Assim:
R A  RB

P1A  P1B .
Assim, a lâmpada 1 brilhará mais quando a chave estiver em A.
Resposta
[E]
da
questão
36:
Para iniciarmos a resolução temos que calcular a tensão real da bateria, ou seja, considerando
o erro de medição de +/–10%.
Vmáx.  16,67  1,1  18,34V
Vmín.  16,67  0,9  15,00V
Como o circuito e o cabo estão aterrados, ambos possuem o mesmo potencial, ou seja,
podemos imaginar o circuito abaixo:
Onde R’ representa a resistência do cabo.
R  R'
Resistência equivalente: Req. 
R  R'
Aplicando a lei de Ohm, para os valores máximo e mínimo de tensão.
Valor máximo:
V
R  R' Vmáx.
10  R' 18,34
R 



i
R  R'
i
10  R'
10
R'máx.  2,25Ω
Valor mínimo:
V
R  R' Vmín.
10  R' 15,00
R 



i
R  R'
i
10  R'
10
R'mín.  1,77Ω
Como o cabo possui resistência de 0,01 /m :
2,25
 xmáx.  225m
0,01
1,77
xmín. 
 xmín.  177m
0,01
xmáx. 
[A] Incorreta. Não conseguimos determinar o comprimento total do cabo devido a sua ruptura
(a parte que se rompeu não faz mais parte do circuito) e a imprecisão do voltímetro.
[B] Incorreta. A distância de aproximadamente 224m é máxima.
[C] Incorreta. A distância de aproximadamente 176m é mínima.
[D] Incorreta. 240m é maior do que a distância máxima.
[E] Correta. 210m está entre as distâncias máxima e mínima.
Resposta
[D]
da
questão
37:
As figuras 1 e 2 ilustram as situações simplificadas com as chaves abertas e fechadas,
respectivamente.
Calculando a corrente I1 (leitura do amperímetro) no circuito da Fig. 1.
Lei de Ohm-Pouillet.
1,5
ε  R I  1,5   300  100  50 I  I 

450
1
I 
A.
300
eq1
1
1
1
1
A diferença de potencial (UBC) entre os pontos B e C é:
 1 
U  100 I  U  100 
 
 300 
1
U  V.
3
BC
1
BC
BC
Quando as chaves são fechadas, a resistência de 50  fica em curto-circuito, podendo ser
descartada, como na Fig.2.
Como a leitura do amperímetro não se altera, a corrente no resistor de 100  continua sendo I1
e a tensão entre os pontos B e C, também não se altera:
U 
BC
1
V.
3
O somatório das tensões entre os pontos A e C é igual à força eletromotriz da bateria,
possibilitando
calcular
a
corrente
1
1
4,5  1
ε  U  U  1,5  300 I 
 1,5   300 I 
 300 I 
3
3
3
I2:
3,5
I 
A.
900
AB
BC
2
2
2
2
Mas, pela lei dos nós:
1
3,5
i I  I  i 

300 900
1
2
 i
3,5  3
900
 i
0,5
A.
900
Finalmente, no resistor de resistência R:
U  Ri 
BC
1
 0,5 
 R

3
 900 
 R
900
1,5

R  600 Ω.
Resposta
[B]
da
questão
38:
Quando usamos um “Tê” para ligar dois ou mais aparelhos, estamos fazendo ligações em
paralelo. Isso aumenta a corrente fornecida pela fonte (no caso, a tomada) e essa sobrecarga
de corrente provoca sobreaquecimento na fiação, aumentando o risco de incêndio.
Resposta
[D]
da
questão
39:
Quando se fecha a chave, surge um campo elétrico ao longo de todo o fio, fazendo com que as
cargas comecem a se deslocar, formando a corrente elétrica.
Resposta
[B]
da
questão
40:
Como o circuito está aberto entre os pontos A e B, a corrente elétrica entre esses pontos é
nula, sendo, portanto, também nula a corrente pelo resistor de R 2 = 4 , ligado ao ponto A; ou
seja, esse resistor não tem função, não entrando no cálculo da resistência equivalente. O
circuito da figura 2 é uma simplificação do circuito da figura 1.
Calculando a resistência equivalente:
Req 
2
 4  5 .
2
A ddp no trecho é U = 5 V, e a ddp entre os pontos A e B (U AB) é a própria ddp no resistor R1.
Assim:
U
5
U  Req I  I 
  1 A.
Req 5
UAB  R1 i  4 1  UAB  4 V.
Resposta
[E]
da
questão
41:
O voltímetro deve ser ligado em paralelo com o trecho de circuito onde se quer medir a tensão
elétrica, ou seja, entre os terminais fase e neutro.
O amperímetro para medir a corrente total deve ser instalado no terminal fase ou no terminal
neutro.
O outro amperímetro para medir a corrente na lâmpada deve ser ligado em série com ela.
Resposta
[A]
da
questão
42:
Como as lâmpadas são idênticas, se ligadas em série, dividirão igualmente a tensão da fonte,
ficando corretamente ligadas, 110 V em cada uma. Para que a perda seja a menor possível, o
fios devem ser os de maior espessura, pois têm menor resistência.
Resposta
[D]
da
questão
43:
Da Lei de Ohm-Pouillet:
E  Req I  20  Req  4   Req  5 .
Os dois resistores do ramo de cima estão em série, totalizando uma resistência de 10 . Os
dois ramos estão em paralelo. Usando a regra do produto pela soma:
10  R x
10  R x
Req 
 5
 10  R x  50  5  R x  5  R x  50 
10  R x
10  R x
R x  10 .
Resposta
[A]
da
questão
44:
Esse é o símbolo para fio terra. O fio terra é um dispositivo para evitar choques elétricos
quando se toca no aparelho.